广义KP-BBM方程的相似、约化、精确解及守恒律

刘 勇，刘希强



广义KP-BBM方程的相似、约化、精确解及守恒律

*刘 勇，刘希强

(聊城大学数学科学学院，山东，聊城 252059)

利用经典李群方法对(2+1)维GKP-BBM方程对称和约化，借助三个辅助方程得到了许多的精确解，并且给出GKP-BBM方程的守恒定律。

李群方法；gkp-bbm方程；精确解；对称约化；守恒律

1 研究前沿

随着科学技术的发展，人们越来越关注于非线性科学。寻找非线性发展方程的精确解已成为一个重要的课题。因此一些有效的方法被提出，试图寻找解决方案的非线发展方程，如扩展的tanh函数展开法[1]，F-函数展开法[2]，指数函数展开法方法[3]，Jacobi椭圆函数展开法[4]，齐次平衡方法[5]，经典和非经典李群方法[6-8]，双曲函数法[9]等。其中的经典李群方法是一种有效的方法。

Wazwaz[10-11]研究 Kadomtsov-Petviashvili- Benjamin-BonaMahony (KP-BBM) 方程

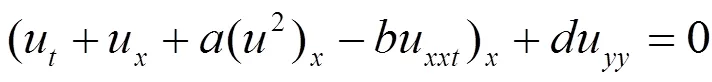
和广义KP-BBM方程

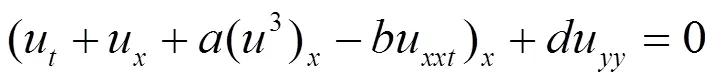
这里，和都是任意常系数。在文献[10-11]中，作者利用sine-cosine法和扩展的tanh法得到方程(1)的一些孤立子解和周期解。Abdou[12]在2008年得到了方程(1)的一些周期解、孤波解和三角函数解。此外，宋明[13]利用分叉法获得了方程(2)的一些平滑周期波形解和周期冲击波解。

方程(2) 转化为：

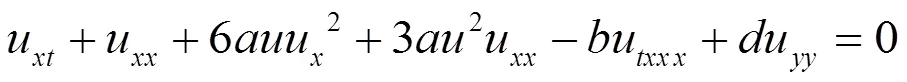
本文利用经典李群方法研究方程(3)。利用经典李群方法是寻找方程(3)对称，并借助对称得到方程(3)的一些相似约化和精确解，包括双曲函数解，三角函数解，有理函数周期解，椭圆函数解等。

本文构成如下: 第二部分，利用严拓的方法得到方程(3)的李典对称群。第三部分，得到方程(3)的相似约化和精确解。第四部分，给出方程(3)的无穷维守恒定律。在第五部分，得到了相关的结论。

2 GKP-BBM方程的经典对称

首先，考虑一个单参数李群的无穷小变换:

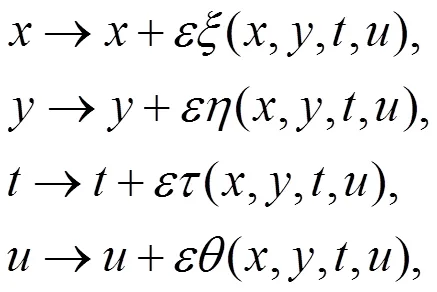
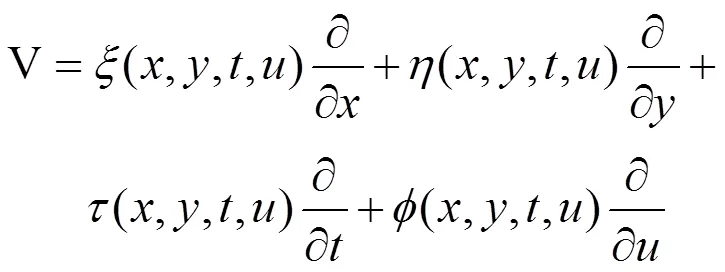
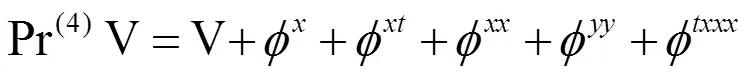
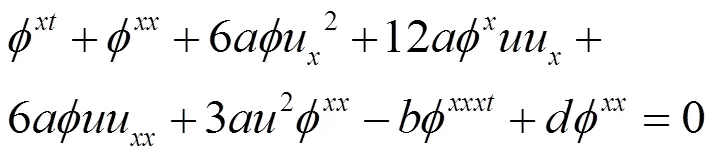
求解此超定方程组可得：

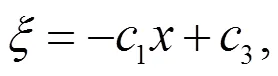
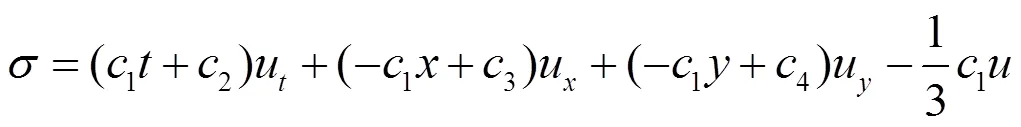
同时，也得到上述对称的生成元：

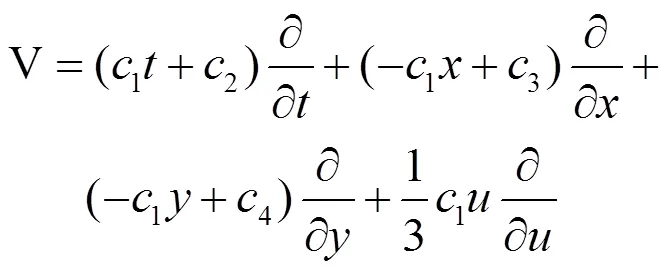
由(10)可得

其算子关系见表1。由表1可知，方程(3)满足一个四维李代数。

表1 李括号运算结果

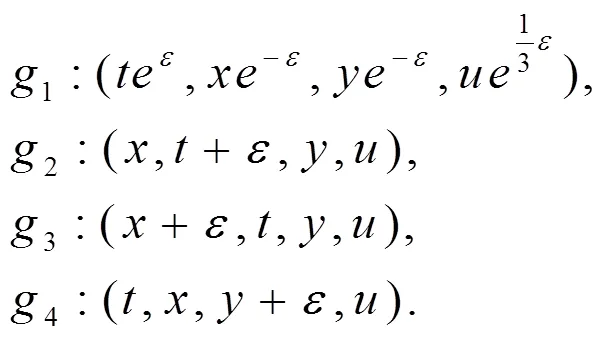
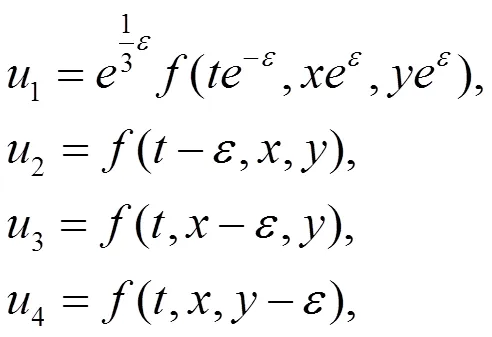
若选取文献[13]中，方程(3)的周期冲击波解：

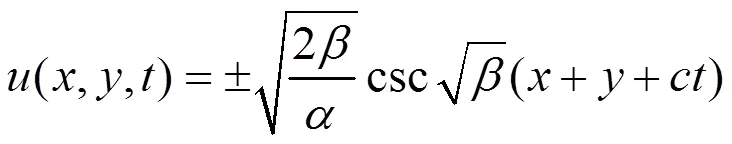
由此可知，将文献[13]中得到的GKP-BBM方程的解进行推广，继而得到大量的新精确解。

3 GKP-BBM方程的约化和精确解

为了求出方程(3)的相似约化和精确解，根据对称(9)式可得到下述对应的特征方程组：

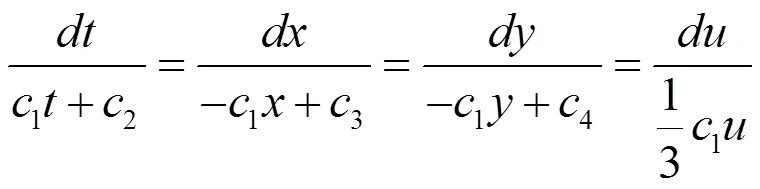
考虑以下四种情况：

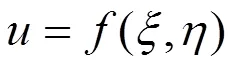
(15)

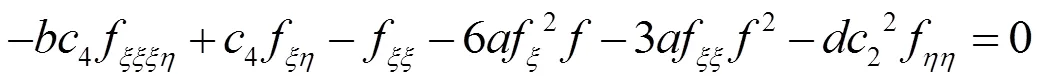
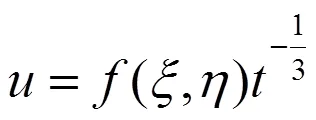
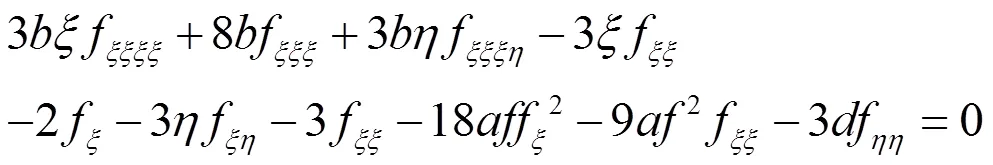
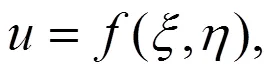
以下考虑情况(a)、(b)、(c)得到方程(3)的精确解。

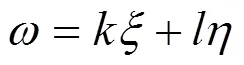
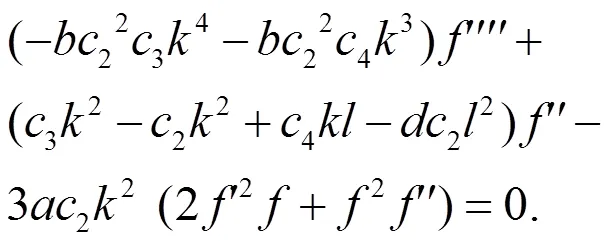
设方程(21)有如下形式的解：

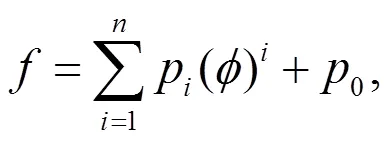
方程（22）转化为：

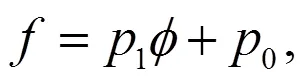
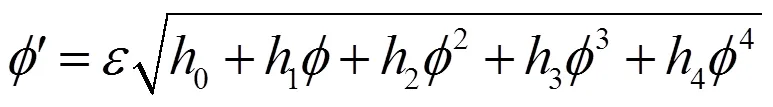
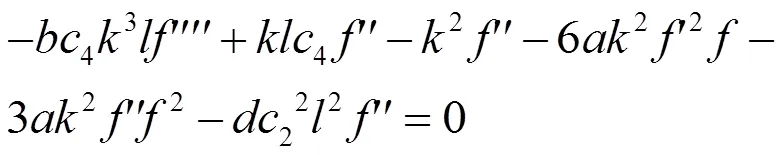
类似情况 1, 设方程(25)有如下解的形式：

(26)

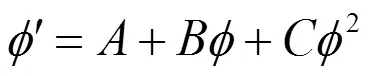
将(26)式和(27)式代入到(25)式, 可以得到如下结果：

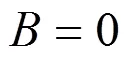
由此, 可以获得如下情况的解：

情况2.1 当方程(3)有七组双曲函数解：

为了得到方程(16)更多的解，以下利用辅助方程[17]求解，

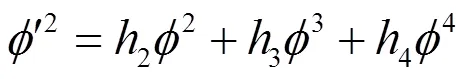
将(26)式和(29) 式代入到(25)式中, 可以得到如下结果：

由此得如下解：

情况 3显然, 方程(18) 具有如下形式的解：

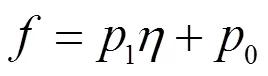
此时方程(3)有一组解

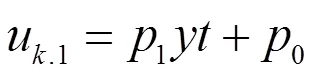
此外, 若设(18) 式有如下形式的解：

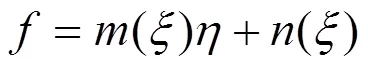
利用(18)式和(30)式, 此时方程(3)有一组解：

情况 4 类似情况 2。这里省略。

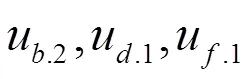
4 GKP-BBM 方程守恒律

为了得到GKP-BBM方程的守恒律，以下介绍所需的符号和定理。

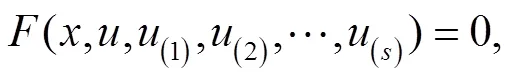
定义1 方程(33)的共轭方程可以定义为如下形式[18-20]：

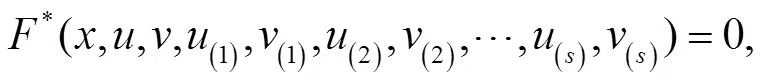
其中

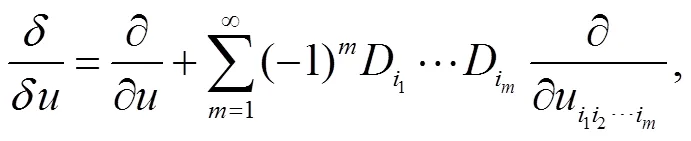
定理1 由方程(33)和它的共轭方程(34)构成的系统[18-20]

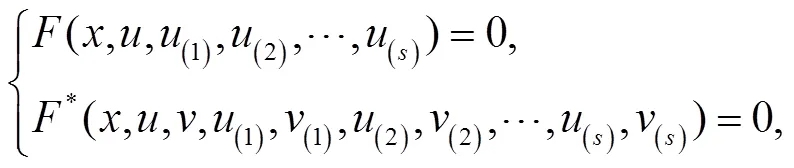
有一个Lagrangian，即：

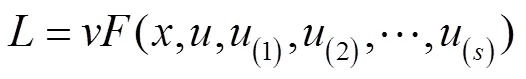
下面介绍由Ibragimov在参考文献[20]中提出的“新的守恒定理”

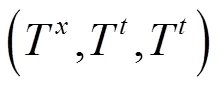
其中是李特征元素且满足

以下利用方程GKP-BBM的对称和共轭方程来研究其守恒律。方程(3)的共轭方程形式如下：

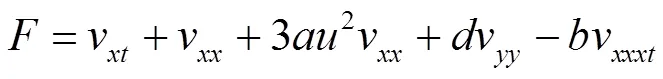
和对称形式下的Lagrangian

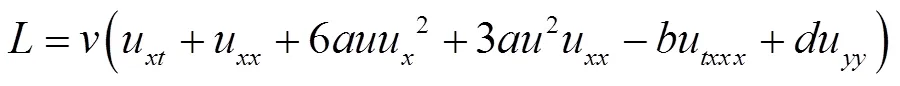
利用定理1, 守恒向量对应的算子如下

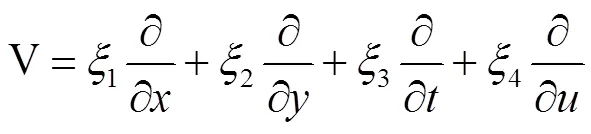
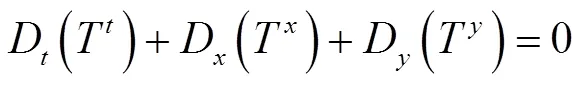
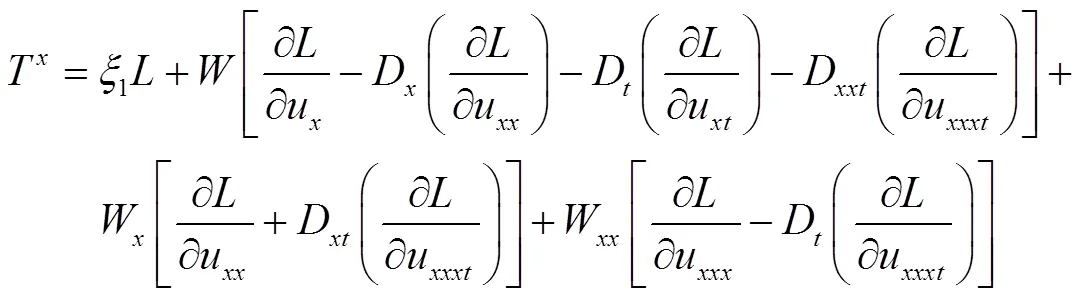
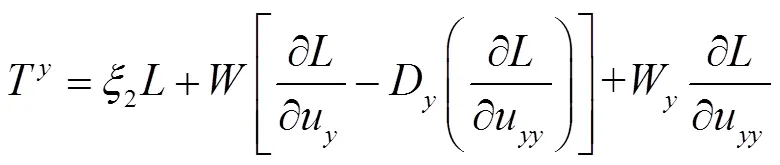
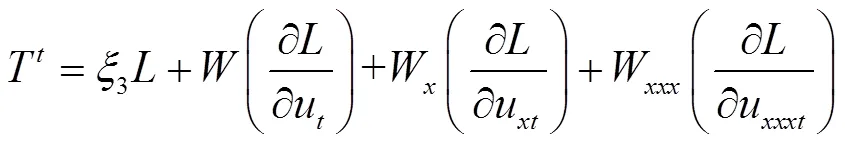
由以上过程可求得算子：

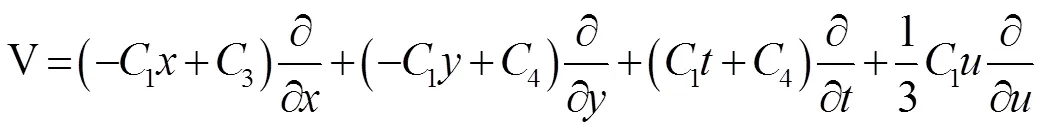
利用这个算子进而得到：

方程(3)的守恒律如下：

5 结论

本文利用经典李群法，得到了GKP-BBM方程的对称，李代数，相似约化。通过求解约化方程得到了GKP-BBM方程大量的精确解，这些精确解在数学物理中有着重要的作用。最后给出了GKP-BBM方程的守恒律。本文的行文过程也有力的说明了李群方法是一个非常有用的方法，值得进一步深入研究。

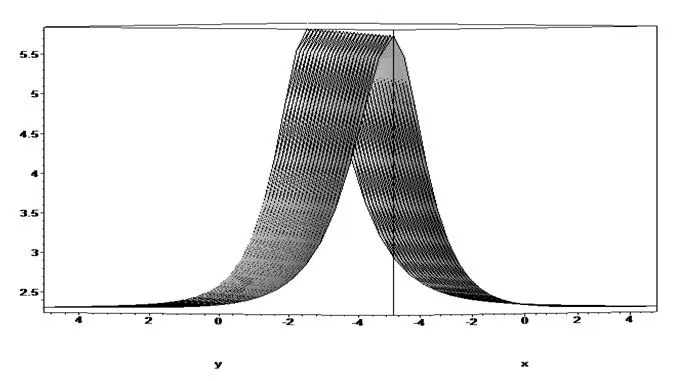
图1 当h2=1,h4=-1,c1=c2=c3=a=h0=b=k=1,t=0,uc.1为钟状解

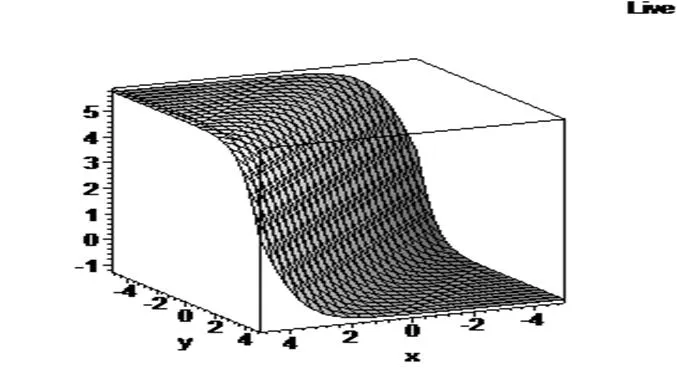
图2 当h2=1,h4=-1,c1=c2=c3=a=h0=b=k=1,t=0,ud.1为扭结解

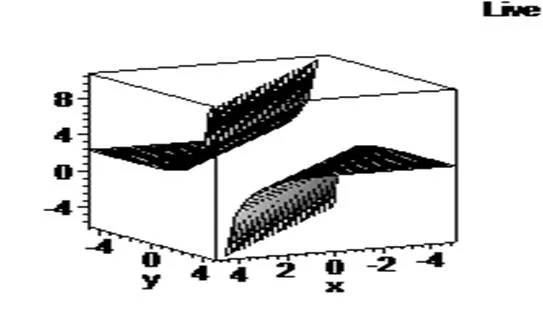
图3 当h2=h4=c1=c2=c3=a=h0=b=k=1,t=0,ue.1为奇异解

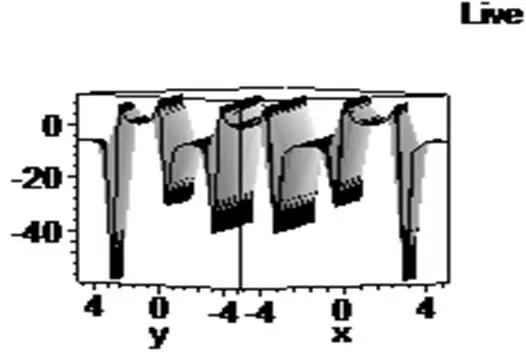
图4 当h2=-1,h4=1,c1=c2=c3=a=h0=b=k=1,t=0,uf.1为三角周期解

[1] Wazwaz A M. The tanh method for travelling wave solution of nonlinear wave equations[J]. Appl. Math. Comput., 2007, 187: 1131-1142.

[2] Abdou M A. The extended F-expansion method and its application for a class of nonlinear evolution equation [J]. Chaos, Soliton Fract, 2007,31:95-104.

[3] He J H, Wu X H. Exp-function method for nonlinear wave equation[J].Chaos, Soliton Fract.,2006(3):700-708.

[4] Fan E G, Zhang J. Applications of the Jacobi elliptic function method to special-type nonlinear equations[J]. Phys. Lett.A ,2002,305:383-392.

[5] Wang M L. Exact solutions of a compound KdV-Burgers equation[J]. Phys. Lett. A, 1996,213: 279-287.

[6] Xin X P, Liu X Q, Zhang Lin-Lin. Explicit solutions of the BK equation[J]. Appl. Math.Comput.,2010,215: 3669-3673.

[7] Liu N, Liu X Q. Similarity reductions and similarity solutions of the (3+1)- dimensional Kadomtsev– Petviashvili equation[J]. Chin. Phys. Lett. 2008,25: 3527-3530.

[8] Wang L, Liu X Q, Dong Z Z. Study of (2+1)-dimensional higher-order Broer–Kaupsystem[J].Commun. Theor.Phys., 2007,47:403-408.

[9] Bai C L, Zhang X, Zhang H. Some new solutions derived from the nonlinear (2+1)-dimensional Toda equation-an efficient method of creating solutions[J]. Chin. Phys. B2009,18: 475.

[10] Wazwaz A M. Exact solutions of compact and noncompact structures for the KP-BBM equation[J]. Applied Mathematics and Computation.2005,169: 700-712.

[11] Wazwaz A M. The extended tanh method for new compact and noncompact solutions for the KP-BBM and the ZK-BBM equations[J]. Chaos,Solitons and Fractals. 2008,38:1505-1516.

[12] Abdou M A. Exact periodic wave solutions to some nonlinear evolution equations[J]. International,Journal of Nonlinear Science. 2008(6):145-153.

[13] Song M, Liu Z R.Periodic Wave Solutions and Their Limits for the Generalized KP-BBM Equation[J]. Journal of Applied Mathematics,. 2012(10): 1155-1180.

[14] Bai C L, Bai C J, Zhao H. A new generalized algebraic method and its application in nonlinear evolution equations with variable coefficients [J].Z. Naturforsch, 2005, 60a: 211-220.

[15] Khalfallah M. Exact traveling wave solutions of the Boussinesq–Burgers equation, Math. Comput[J]. Model,2009,49:666-671.

[16] Yan Z Y, H Zhang Q. New explicit solitary wave solutions and periodic wave solutions for Whitham-Broer- Kaup equation in shallow water[J]. Phys. Lett. A, 2001,285: 355-362.

[17] Sirendaoreji, Sun J. Auxiliary equations method for solving nonlinear partial differential equations[J]. Phys, Lett. A , 2003,309:387-396.

[18] Zhang L H. Conservation laws of the (2 + 1)-dimensional KP equation and Burgers equation with variable coefficients and cross terms[J]. Applied Mathematics and Computation, 2013,219: 4865-4867.

[19] Wang G W, Liu X Q, Zhang Y Y. Symmetry reduction, exact solutions and conservation laws of a new fifth-order nonlinear integrable equation[J]. Commun Nonlinear Sci Number simulat, 2013,18:2313-2320.

[20] Ibragimov NH. A new conservation theorem[J]. J Math Anal Appl: 2007, 333:311-328.

SYMMETRY REDUCTIONS, EXACT SOLUTIONS AND CONSERVATION LAWS OF THE GENERALIZED KADOMTSOV- PETVIASHVILI- BENJAMIN-BONAMAHONY EQUATION

*LIU Yong, LIU Xi-qiang

(School of Mathematical Sciences, Liaocheng University, Liaocheng, Shandong 252059, China)

Based on the classical Lie group method, we find the classical symmetry and reductions of (2+1)-dimensional GKP-BBM equation.Some new solutions of the solutions should be derived by applying three auxiliary equations. Furthermore, we give the conservation laws of theGKP-BBM equation.

Lie group method; GKP-BBM equation; exact solutions; symmetry reduction; conservation laws

1674-8085(2014)01-0001-07

O175.2

A

10.3969/j.issn.1674-8085.2014.01.001

2013-09-23；

2013-12-05

国家自然科学基金委员会-中国工程物理研究院联合基金项目(11076015)

*刘 勇(1982-)，男，山东枣庄人，硕士生，主要从事非线性发展方程求解研究(E-mail: liuyong0616@163.com);

刘希强(1957-)，男，山东菏泽人，教授，博士，主要从事非线性发展方程系统研究(E-mail:liuxq@sina.com).