高速公路旅行时间的自适应插值卡尔曼滤波预测*

赵建东 王浩 刘文辉

(北京交通大学机械与电子控制工程学院，北京100044)

基于Sage-Husa自适应卡尔曼滤波算法的站间旅行时间预测原理如下:

步骤1 初始化状态最优估计X(0)、状态向量后验估计P(0)、系统噪声方差矩阵Q(0)、系统观测方差R(0)及遗忘因子b.

步骤2 依据1.4节的卡尔曼滤波模型建立旅行时间预测模型.

步骤3 递推计算状态向量误差先验估计)、滤波增益矩阵K(t)、状态先验估计及新息ε(t):

式中:Q(t－1)、R(t－1)为t周期系统噪声方差矩阵和观测方差;T(t)为t周期的实际平均旅行时间，滤波计算过程以T(t－1)代替.

步骤4 更新状态最优估计¯X(t)和状态向量误差后验估计P(t):

旅行时间指车辆从始发地到目的地的行驶时间，可衡量所经路段的通行效率和交通状态［1］，是交管部门交通控制和诱导的重要依据［2］，也是出行者高度关注的首要信息［3］.当前，旅行时间已成为先进出行者信息系统(ATIS)和路径导航系统(RGS)的关键因素［3］，其计算和预测结果的精确度与时效性直接影响动态交通管理效果［4］和出行者路径选择［1］.

近年来，国内外学者围绕旅行时间预测理论及应用开展了深入研究.熊文华等［2］融合浮动车全球定位系统(GPS)和线圈车检器数据，基于BP网络建立了城市道路旅行时间预测仿真模型.李惠兵等［4］融合线圈车检器检测的交通流密度、交通量，以及浮动车行程时间估计值、样本量，采用BP神经网络仿真预测主干道旅行时间.Zhu等［3］利用分级群聚法获取影响旅行时间的时间及空间因素，基于海量的浮动车数据和卡尔曼滤波方法预测主干道车辆旅行时间.Lelitha等［1］利用高速公路上间隔250 m布设的线圈车检器，采集流量、占有率、速度，针对样本数据量少的问题，基于支持向量机(SVM)研究短周期旅行时间预测.Luou等［5］利用时空间插值的数据填充方法弥补断面检测数据的不足和错误，将时间平均速度转换为空间平均速度，仿真预测旅行时间.Hwang等［6］融合线圈车检器和浮动车两种数据，提出一种动态加权融合方案来预测市区道路旅行时间，并与单一数据源预测方法对比，指出数据稀疏性会破坏算法稳定性.李进燕等［7］运用城市道路网实时和历史数据，基于简化路网模型的卡尔曼滤波多步行程时间预测算法，解决因一段时间内没有观测值而无法预测的问题.温惠英等［8］为改善卡尔曼滤波用于时间序列预测的自适应性能，利用灰色关联分析影响行程时间的因素，基于卡尔曼滤波递推仿真预测干道旅程时间.胡小文［9］研究了旅行时间与交通流量、占有率的关系，融合探测车和断面检测器数据，采用非参数统计方法(K-近邻法)和Sage-Husa自适应卡尔曼滤波算法仿真预测城市道路旅行时间.Yang［10］利用GPS检测车测试指定路段行程时间，基于时间离散递归卡尔曼滤波算法仿真预测拥堵状态下的旅行时间，并指出预测精度与数据节点数、历史数据及预测周期等有关.Mehmet等［11］采用瓶颈识别算法检测历史交通事件，基于高斯混合模型分类构建历史数据库和随机拥堵地图，并将地图与速度估计曲线阈值相匹配，然后利用交通拥堵搜索算法搜索实时与历史数据，预测高速公路拥堵状况行程时间.杨兆升等［12］针对非常态事件对道路交通运行的影响，分别分析GPS数据样本充足和不足的情况，基于BP神经网络融合方法模拟预测重大交通事故和大雾情况下的行程时间.Soriguera等［13］利用高速公路收费入口站和出口站的票据信息，统计车辆主线站间平均行驶时间，指出应融合站间断面数据估计旅行时间.Yoshikazu等［14］利用统计学方法和历史数据，研究了交通量极小、夜间、局部交通量小而整体交通量大等情况下的旅行时间计算方法，指出利用收费数据计算旅行时间存在异常数据难以剔除和样本量小的问题.赵建东等［15］针对高速公路断面数据密度不足以及卡尔曼滤波模型非线性性能弱的现状，将等间距插值法引入卡尔曼滤波算法，基于收费数据预测高速公路站间旅行时间，预测精度较常规卡尔曼滤波有较大提高，但非平稳交通流状态下的预测精度不稳定.

综上可知，现有的旅行时间研究对象多为城市道路和高速公路;数据源以车检器、浮动车数据为主，收费数据应用较少;算法有历史趋势法、时间序列法、回归分析法、支持向量机、神经网络、卡尔曼滤波等，其中卡尔曼滤波涉及的交通参数少、实时性强，应用较多;预测验证多为仿真，应用较少.同时，由于交通事故、拥堵等不确定性突发事件的日益增多，导致车辆旅行时间的不确定性显著增加，这使得如何提高旅行时间预测算法的适应性成为关键问题.

图1 旅行时间预测原理Fig.1 Principle of travel time prediction

鉴于此，为进一步解决非平稳交通流状态下因卡尔曼滤波算法自适应性能差而导致的预测精度不稳定问题，文中在文献［15］的基础上，将状态方程模型优化为时变模型，引入Sage-Husa自适应卡尔曼滤波算法，开发旅行时间预测系统，并依托京港澳高速公路北京段进行实例验证.

1 站间旅行时间预测原理

我国高速公路有人工半自动收费(MTC)和电子不停车收费(ETC)两种数据，单辆车的旅行时间可由出口站时间减入口站时间计算得到［15］.

高速公路站间旅行时间预测原理如图1所示，包括收费数据融合、平均旅行时间计算、等间距插值、卡尔曼滤波模型搭建及Sage-Husa自适应卡尔曼滤波算法原理5部分.其中:T(t)为统计得到的t周期车辆平均旅行时间;ε(t)为滤波后新息［9］;为t－1、t周期状态向量最优估计;为t周期状态向量先验估计;Q(t－1)、R(t－1)为t－1周期系统噪声方差矩阵和观测方差;K(t)为滤波过程中滤波增益矩阵;A(t)、B为卡尔曼滤波模型的状态转移矩阵和观测矩阵.

1.1 收费数据融合

统计分析收费数据可知，多种主客观因素易产生异常旅行时间数据;MTC数据包含等待缴费时间，而ETC数据不含等待缴费时间.为提高周期内车辆样本的质量与数量，MTC和ETC数据融合原则如下:

(1)若单辆车旅行时间远大于或远小于站间车辆旅行时间，则可能为异常旅行时间数据;若临近车辆旅行时间也远大于或远小于站间车辆旅行时间，可说明路段交通状态异常，因此，单辆车旅行时间数据正常.

(2)若ETC、MTC车道车辆旅行时间差值满足预测所能容纳的最大误差，则融合应用两者数据.

1.2 平均旅行时间计算

车辆行驶速度的随机性导致单辆车旅行时间与道路真实旅行时间之间的偏差浮动较大，为缩小偏差浮动范围，提高平均旅行时间计算的准确度，将数据剔除方法引入平均旅行时间计算模型，原理如下:

式中:Tmean为N辆车的平均旅行时间;Tinterval为周期内有效旅行时间区间，车辆旅行时间Ti(i=1，2，…，N－1，N)落在该区间内则有效;C1、C2为通过历史数据确定的筛选系数;Taverage为筛选后周期内反映交通状态的R辆车的平均旅行时间.

1.3 数据等间距插值

数据插值可增加平均旅行时间序列间的数据节点，减少平均旅行时间序列数值的跳变，提高模型准确度.由于t周期旅行时间为预测时间，故需向前推移一个周期.兼顾当天的、历史日期的t－2、t－3周期旅行时间各自对实时t－1周期旅行时间的影响，利用等间距插值方法重构时间序列原理如下:

式中:TiMax和TiMin为第t－i周期旅行时间的最大值与最小值;THUi和THDi为历史日期中t－i周期旅行时间的最大值与最小值;TNi为实时t－i周期的旅行时间;i=2，3.

式中:j为所增加数据节点的最大值;TNki为当实时t－i周期旅行时间随历史t－i周期旅行时间变动时，对实时t－1周期旅行时间的影响值;TN1为实时t－1周期的旅行时间;0≤k≤j.

依据上述原理，重构时间序列如下:

式中，TSt－1、TSt－2、TSt－3为等间距插值处理后 t－1、t－2、t－3周期新的时间序列.

1.4 卡尔曼滤波模型搭建

卡尔曼滤波模型［15］由状态方程与观测方程组成，如式(11)和(12)所示:

式中:X(t)为n维状态变量;A(t)为状态转移矩阵;w(t)为系统噪声矩阵;TY(t)为预测的t周期旅行时间;B为观测矩阵;¯X(t)为状态变量最优估计;v(t)为测量噪声.

(1)状态方程

取两个相邻周期的旅行时间为一状态，即

由此推导出状态方程:

式中:w(t)为1×2阶高斯白噪声矩阵;r1和r2分别为t－1和t－2周期的旅行时间共同对t周期旅行时间的影响系数.

将时间序列向前推移一个周期，基于最小二乘法求取r1、r2的原理如下:

式中:TS为TSt－2、TSt－3组成的新时间序列.

(2)观测方程

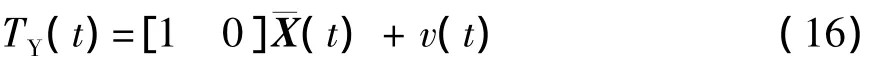
1.5 Sage-Husa自适应卡尔曼滤波预测原理

基于Sage-Husa自适应卡尔曼滤波算法的站间旅行时间预测原理如下:

步骤1 初始化状态最优估计X(0)、状态向量后验估计P(0)、系统噪声方差矩阵Q(0)、系统观测方差R(0)及遗忘因子b.

步骤2 依据1.4节的卡尔曼滤波模型建立旅行时间预测模型.

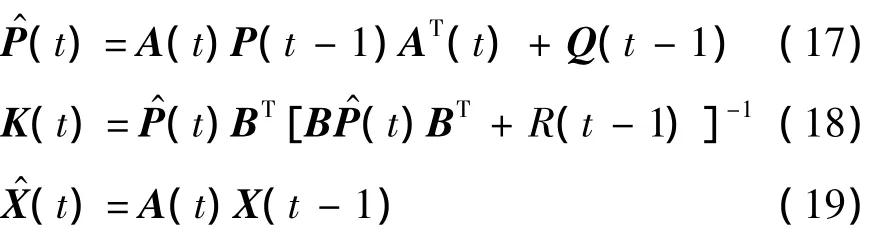
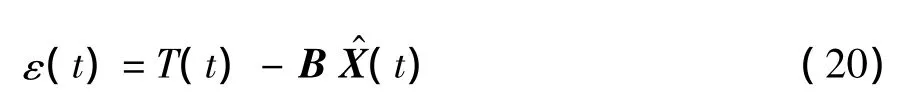
式中:Q(t－1)、R(t－1)为t周期系统噪声方差矩阵和观测方差;T(t)为t周期的实际平均旅行时间，滤波计算过程以T(t－1)代替.

步骤4 更新状态最优估计¯X(t)和状态向量误差后验估计P(t):

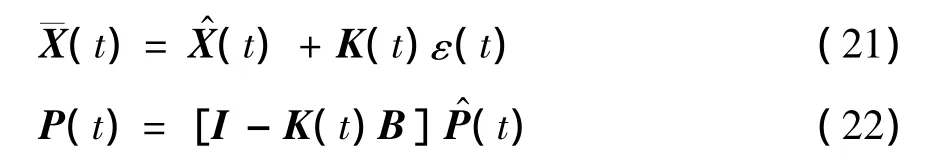
步骤5 卡尔曼滤波自适应更新系统噪声方差矩阵Q(t)和系统观测方差R(t):

乳腺癌是临床上常见的一种恶性肿瘤疾病，近年来发病人群不断趋于年轻化且人数也逐渐上升，患者在早期出现乳房不同程度疼痛、乳房肿胀和乳头内陷等症状，对患者的生活造成困扰。 因此，加强对乳腺癌患者的早期检查，并及早治疗十分有必要。

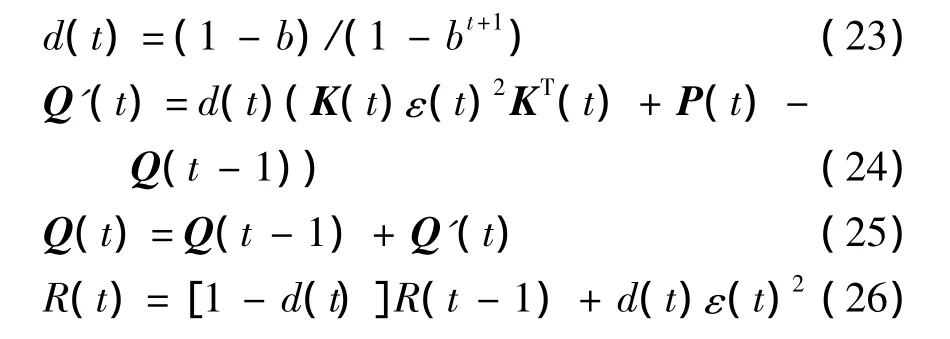
式中，d(t)为遗忘系数.

步骤6 预测t周期旅行时间TY(t):

步骤7 令t=t+1，返回步骤2循环计算，直至旅行时间预测结束.

2 算法应用

文中选取京港澳高速公路(G4)北京段站间距离9.6 km、交通量达3000辆/日、小型车约占97%的京良路收费站至杜家坎收费站进京路段进行算法验证［15］，对比插值前、后的卡尔曼滤波算法和插值自适应卡尔曼滤波算法，分别预测正常、事故及小长假3种交通流状态下的车辆站间旅行时间，预测周期取10min.

2.1 性能评价指标

文中采用相对误差、平均相对误差、事故周期平均相对误差评价预测结果精度［15］，

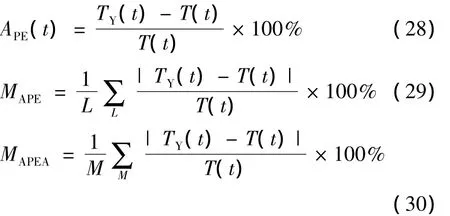
式中，APE(t)为t周期预测相对误差，MAPE为所有周期平均相对误差，MAPEA为事故周期平均相对误差，L为一天内预测周期总数，M为一天内事故周期总数.

2.2 预测结果与误差分析

2.2.1 正常交通流状态

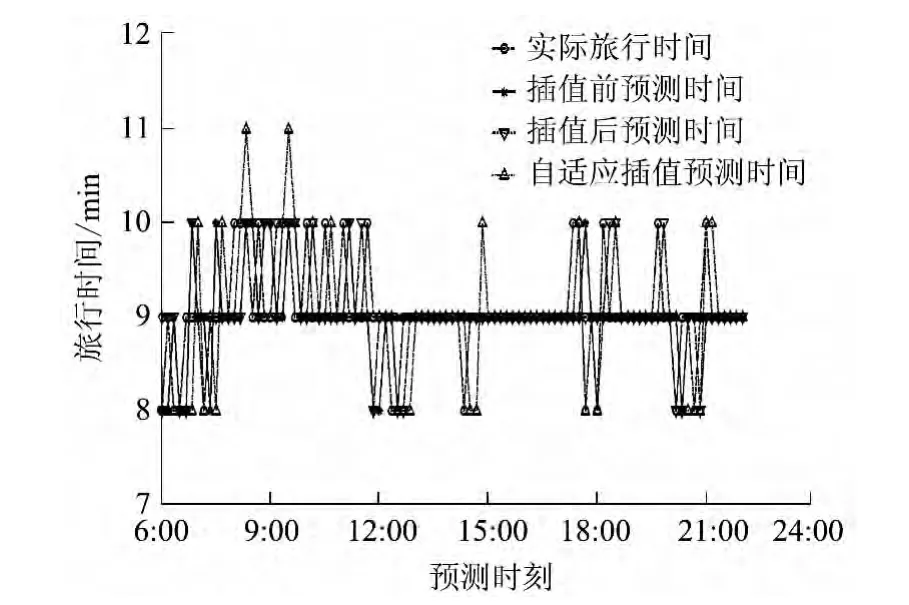
图2 正常交通流状态下的旅行时间预测曲线Fig.2 Travel time prediction curves under normal traffic flow

3种算法的旅行时间预测误差曲线如图3所示，旅行时间预测误差性能评价指标如表1所示.

由图3可见，相比于插值后算法自适应插值算法预测相对误差更小.由表1可知，自适应插值算法的MAPE降低至4.03%，预测精度适用于正常交通流状态下的旅行时间预测要求.

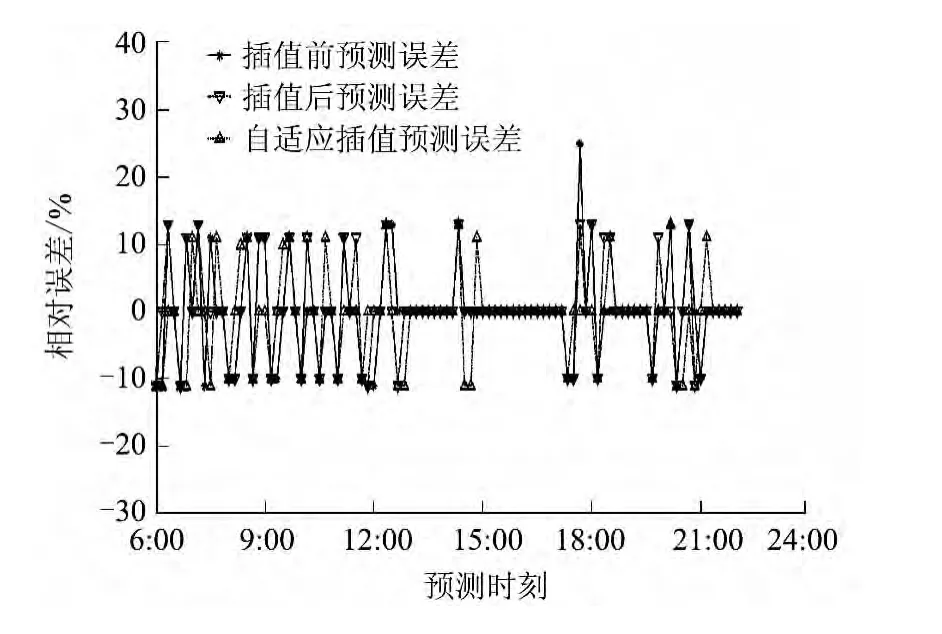
图3 正常交通流状态下的旅行时间预测误差曲线Fig.3 Curves of travel time prediction error under normal traffic flow

表1 正常交通流状态下的旅行时间预测误差性能评价指标Table 1 Evaluation indexes of travel time prediction error under normal traffic flow

2.2.2 事故交通流状态

事故交通流状态下，3种算法的旅行时间预测曲线如图4所示.由图4可见，14:30路段交通异常，发生交通事故，且15:40至17:20交通中断，事故周期内自适应插值算法比插值后算法的预测时间更加接近实际时间，其余周期内3种算法的预测时间与实际时间比较一致.

图4 事故交通流状态下的旅行时间预测曲线Fig.4 Travel time prediction curves under accident traffic flow

不同算法的旅行时间预测误差曲线如图5所示，旅行时间预测误差性能评价指标如表2所示.

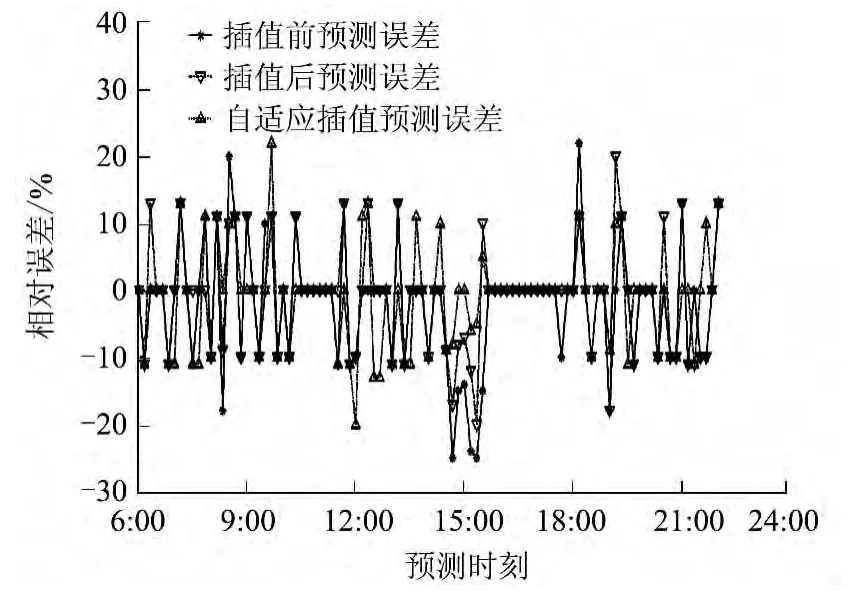
图5 事故交通流状态下的旅行时间预测误差曲线Fig.5 Curves of travel time prediction error under accident traffic flow

统计14:30至15:30内7个事故周期的相对误差数据，旅行时间预测相对误差低于15%的周期个数由插值前的3个提高到插值后的5个，自适应插值算法较插值后又增加了2个，预测精度进一步提高.表2与图5相对应，自适应插值算法事故周期内的APE区间降低到(－9%，5%)，MAPEA降低到6.31%，预测精度稳定性满足事故交通流状态下的旅行时间预测要求.

表2 事故交通流状态下的旅行时间预测误差性能评价指标Table 2 Evaluation indexes of travel time prediction error under accident traffic flow

2.2.3 小长假交通流状态

小长假交通流状态下，3种算法的旅行时间预测曲线如图6所示.

图6 小长假交通流状态下的旅行时间预测曲线Fig.6 Travel time prediction curves under holiday traffic flow

由图6可见，小长假交通流不稳定，10:00至11:00时段路面发生轻微拥堵，16:00至18:40时段发生交通事故，事故周期内自适应插值算法比插值后算法的预测时间更加接近实际旅行时间，其余周期内3种算法的预测时间与实际时间相当一致.

不同算法的旅行时间预测误差曲线如图7所示，旅行时间预测误差性能评价指标如表3所示。

统计16:00至18:40内17个事故周期的相对误差数据，旅行时间预测相对误差低于15%的周期个数由插值前的9个提高到插值后的10个，自适应插值算法较插值后又增加了3个，预测精度进一步提高.表3与图7相对应，自适应插值算法事故周期内的APE区间降低到(－16%，20%)，MAPEA降低到9.50%，预测精度稳定性满足小长假交通流状态下的旅行时间预测要求.

图7 小长假交通流状态下的旅行时间预测误差曲线Fig.7 Curves of travel time prediction error under holiday traffic flow

表3 小长假交通流状态下的旅行时间预测误差性能评价指标Table 3 Evaluation indexes of travel time prediction error under holiday traffic flow

3 系统应用

根据上述基于等间距插值与Sage-Husa自适应卡尔曼滤波的旅行时间预测算法，笔者基于.NET、SQL Server开发了一套实时高速公路站间旅行时间预测系统，其应用界面如图8所示.目前所开发的系统已嵌入路网运行状态分析中，实际应用表明，正常、事故、小长假3种交通流状态下旅行时间预测精确度高，可为交通出行提供服务支撑.

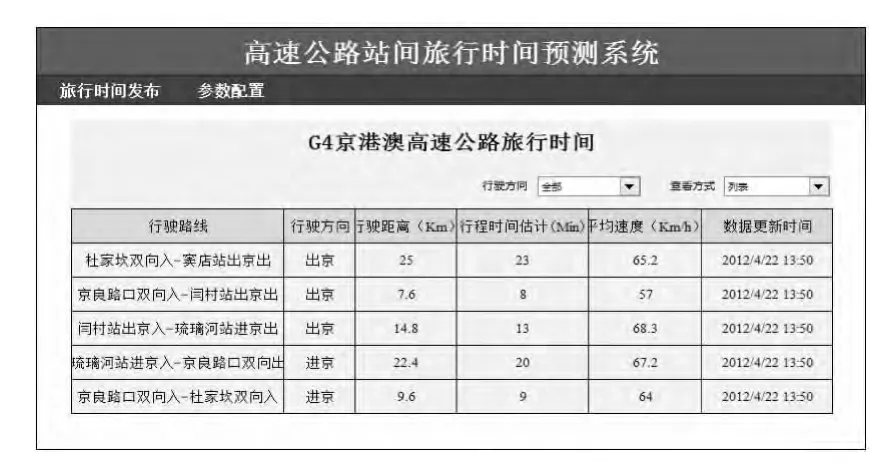
图8 旅行时间预测应用系统Fig.8 Application system of travel time prediction

4 结论

(1)文中提出了一套融合MTC和ETC数据的实时处理方法，增强了数据可靠度;改进后的平均旅行时间计算模型兼具异常数据剔除，提高了平均旅行时间计算的准确度.

(2)文中引入等间距插值方法重构实时及历史旅行时间之间的时间序列，并基于最小二乘法实时搭建卡尔曼滤波模型，提高了模型的准确度.

(3)自适应插值卡尔曼滤波算法对平稳交通流及非平稳交通流状态下的旅行时间均具有较高的预测精度，且明显降低了事故周期的平均相对误差.

(4)旅行时间预测系统在示范路段的应用表明，自适应插值卡尔曼滤波预测算法适应性强，预测结果准确度高，可为交通管控和出行诱导提供良好数据支撑.

［1］ Lelitha Vanajakshi，Rilett Laurence R.Support vector machine technique for the short term prediction of travel time［C］∥Proceedings of the 2007 IEEE Intelligent Vehicles Symposium.Istanbul:IEEE Intelligent Transportation Systems Society，2007:600-605.

［2］ 熊文华，徐建闽，林思.基于BP网络的浮动车与线圈检测数据融合模型［J］.计算机仿真，2009，26(9): 235-238.Xiong Wen-hua，Xu Jian-min，Lin Si.A fusion model for floating vehicle and loop detector data based on BP network［J］.Computer Simulation，2009，26(9):235-238.

［3］ Zhu T Y，Kong X P，Lv W F.Large-scale travel time prediction for urban arterial roads based on kalman filter［C］∥Proceedings of 2009 International Conference on Computational Intelligence and Software Engineering.Wuhan: IEEE Wuhan Section，2009:1-5.

［4］ 李惠兵，杨晓光.面向行程时间预测准确度评价的数据融合方法［J］.同济大学学报:自然科学版，2013，41 (1):60-65.

Li Hui-bing，Yang Xiao-guang.Data fusion method for accuracy evaluation of travel time forecast［J］.Journal of Tongji University:Natural Science Edition，2013，41(1): 60-65.

［5］ Luou Shen，Mohammed Hadi.Practical approach for travel time estimation from point traffic detector data［J］.Journal of Advanced Transportation，2013，47(5):526-535.

［6］ Hwang K P，Lee W H，Wu W B.Travel time prediction by weighted fusion of probing vehicles and vehicle detectors data sources［C］∥Proceedings of the 12th International Confe-rence on ITS Telecommunications.Taibei:IEEE Communication Society，2012:476-481.

［7］ 李进燕，朱征宇，刘琳，等.基于简化路网模型的卡尔曼滤波多步行程时间预测方法［J］.系统工程理论与实践，2013，33(5):1289-1297.Li Jin-yan，Zhu Zheng-yu，Liu Lin，et al.Multi-step kalman filtering travel time estimation method based on simplified road network model［J］.Systems Engineer-Theory＆Practice，2013，33(5):1289-1297.

［8］ 温惠英，徐建闽，傅惠.基于灰色关联分析的路段行程时间卡尔曼滤波预测算法［J］.华南理工大学学报:自然科学版，2006，34(9):66-69.Wen Hui-ying，Xu Jian-min，Fu Hui.Estimation algorithm with kalman filtering for road travel time based on grey relation analysis［J］.Journal of South China University of Technology:Natural Science Edition，2006，34(9):66-69.

［9］ 胡小文.基于探测车数据和定点检测器数据的路段行程时间估计［D］.上海:同济大学交通运输工程学院，2008.

［10］ Yang J S.Travel time prediction using the GPS test vehicle and kalman filtering techniques［C］∥Procee-dings of the 2005 American Control Conference.Portland:A-merica Automatic Control Council，2005:2128-2133.

［11］ Mehmet Yildirimoglu，Nikolas Geroliminis.Experienced travel time prediction for congested freeways［J］.Transportation Research(Part B):Methodological，2013，53: 45-63.

［12］ 杨兆升，莫祥伦，于尧，等.非常态下路段行程时间估计方法［J］.吉林大学学报:工学版，2013，43(6): 1459-1465.Yang Zhao-sheng，Mo Xiang-lun，Yu Yao，et al.Estimation of travel time under abnormal state［J］.Journal of Jilin University:Engineering and Technology Edition，2013，43(6):1459-1465.

［13］ Soriguera F，Rosas D，Robuste F.Travel time measurement in closed toll highways［J］.Transportation Research Part B:Methodological，2010，44(10):1242-1267.

［14］ Yoshikazu Ohba，Hideki Ueno，Masao Kuwahara.Travel time calculation method for expressway using toll collection system data［C］∥Proceedings of IEEE/IEEJ/JSAI International Conference on Intelligent Transportation Systems.Tokyo:IEEE Intelligent Transportation System Council，1999，471-475.

［15］ 赵建东，王浩，刘文辉，等.基于收费数据的高速公路站间旅行时间预测［J］.同济大学学报:自然科学版，2013，41(12):1849-1854.Zhao Jian-dong，Wang Hao，Liu Wen-hui，et al.Highway travel time prediction between stations based on Toll ticket data［J］.Journal of Tongji University:Natural Science Edition，2013，41(12):1849-1854.