多模式交通网络下的城市交通出行链行为模型*
周家中 张殿业
(1.西南交通大学交通运输与物流学院,四川成都610031;2.马里兰大学国家精明增长研究中心,大学公园市20742)
城市交通出行者为达到各种出行目的,通过不同交通方式在城市空间内发生的位移构成了复杂的城市交通系统.因此,居民出行行为是城市交通系统研究的核心理论基础[1].出行链行为研究是城市交通出行行为研究的重要部分.出行链描述了出行者从起始点出发,经过若干个目的地,再返回起始点的出行全过程,它摒弃了传统交通行为模型中表征每一次出行的孤立静态性,真实揭示了城市交通出行全过程的连续性特征,体现了城市交通出行行为研究的连续动态性,因此,出行链行为的研究对城市居民出行行为研究有重要意义[2-8].
已有的出行链行为模型主要可以分为两类:基于马尔科夫链的出行链行为模型;基于效用理论的出行链行为非集计离散选择模型.前者的研究以Sasaki[9]和Lerman[10]为代表;后者在国内外已有较多研究,其中代表性研究为Bowman等[11]提出的基于日活动计划的出行链模型,另外,隽志才等[12]基于活动链对出行需求预测方法进行了研究.但已有模型存在以下不足:基于马尔科夫链的出行链行为模型假设出行链的变化过程符合马尔科夫过程,但是至今少有证据表明出行链行为符合马尔科夫特性,因此基于马尔科夫链对出行链的研究缺乏理论依据;城市交通出行链一般包含多次出行,具有灵活多变的特质,而基于效用理论的离散模型很难鉴别出行链内部每一次出行的效用,同时离散模型对个体数据质量要求更高,国内大多缺乏良好的数据储备,这也进一步制约了离散模型的应用.
针对以上不足,结合出行链的空间连续分布特征,文中提出运用在空间分布方面具有显著优势的最大熵模型[13]对出行链行为进行研究.在目前已有研究中,最大熵模型主要是应用于传统的交通出行分布预测[14-15],而在出行链行为方面的研究较为薄弱,Honma等[15]的研究在出行链模型的限制条件设置中缺乏深入考虑,缺乏多模式交通网络的背景引入,使模型有应用局限性.
据此,文中基于已有研究基础,在多模式交通网络背景下运用最大熵模型对城市交通出行链行为进行分析研究,并对模型的有效性进行了应用验证.
1 出行链行为模型基础
1.1 出行链的基本概念
出行链是指出行者为完成若干目的,在一定时间顺序上的若干个连续出行构成的链接形式.城市交通出行行为具有灵活多变的复杂特性,而城市交通出行链是对城市交通出行者的出行全过程的真实刻画.
文中模型假设sRt代表ψ+1次出行的出行链,出行链路径定义如下:

其中,s={1,2,…,S}和t={1,2,…,T}分别代表出发小区和到达小区编号集合,Rt={t1,t2,…,tψ}为ψ维的到达小区选择集.出行链如下图1所示.

图1 出行链的示意图Fig.1 Schematic plan of trip chain
1.2 简单出行链的可能路径示例
为更加直观地了解文中建模思想,下面对简单出行链的可能路径进行简要分析.
假设有2个出发小区s={1,2}、2个到达小区t={1,2},到达小区选择集维数ψ≤2,则出行链的可能路径如图2所示(图中椭圆代表出发小区,矩形代表到达小区).具体如下:
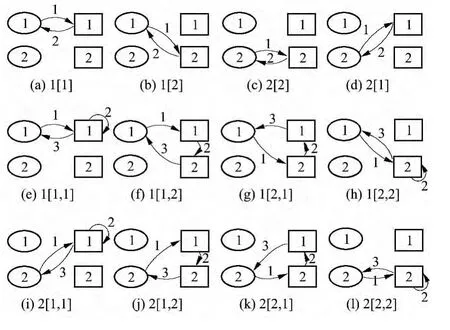
图2 简单出行链的可能路径Fig.2 Possible paths of simple trip chain
(1)到达小区数量为1的出行链(ψ=1)
出发小区数量(2个)×到达小区数量(2个)= 4个.
(2)到达小区数量为2的出行链(ψ=2)
出发小区数量(2个)×第一次到达小区数量(2个)×第二次到达小区数量(2个)=8个.
因此,出行链的可能路径共计12个.
2 出行链行为最大熵模型的构建
2.1 模型建立
令CsRt为采用出行链sRt出行的出行量.同时为了模型简化,假设最大到达小区数量为N,即有1≤ψ≤N.
模型目标为基于最大熵原理估计所有出行链路径sRt的出行量CsRt.CsRt服从出行链OD(起讫点)限制及多模式网络下出行链距离限制两个限制条件.
2.1.1 出行链OD限制条件
出行链OD限制条件见式(1):

式中,Os为s小区的出行发生量,Dt为t小区的到达出行链数量,RΘ为出行者的到达小区选择集,表示从s小区出发的所有出行链路径的出行量,n表示在出行链中将小区t作为第n个到达小区的出行链数量.令C为出行链总量,则有

式中,到达小区的出行链数量Dt的求和大于出行链总量,原因在于一个出行链中包含有多个到达小区.
2.1.2 多模式网络下的出行链距离限制条件
城市交通网络是复杂多模式网络,为更准确地描述出行链的距离限制条件,模型基于多模式交通网络定义出行链多模式网络加权出行距离dsRt构建多模式网络下的出行链阻抗限制条件,如式(3)所示:

式中,d为多模式网络下出行总距离,dsRt为出行链sRt的多模式网络加权出行距离,和分别表示出行链sRt的道路网络距离、公交网络距离和轨道网络距离,分别为出行链 sRt的道路交通分担率、公交分担率和轨道交通分担率.以上数据均由城市交通模型中各交通小区间的各出行方式下的小区距离矩阵和出行方式分担率矩阵计算得到.
令PsRt为出行链sRt的先验概率,则有

令P(CsRt)为出行链sRt的发生概率,构建多项式概率分布函数如下:

根据最大熵原理,P(sRt)取最大值时即为出行链行为模型所求.因此,模型转化为最优化目标规划问题:
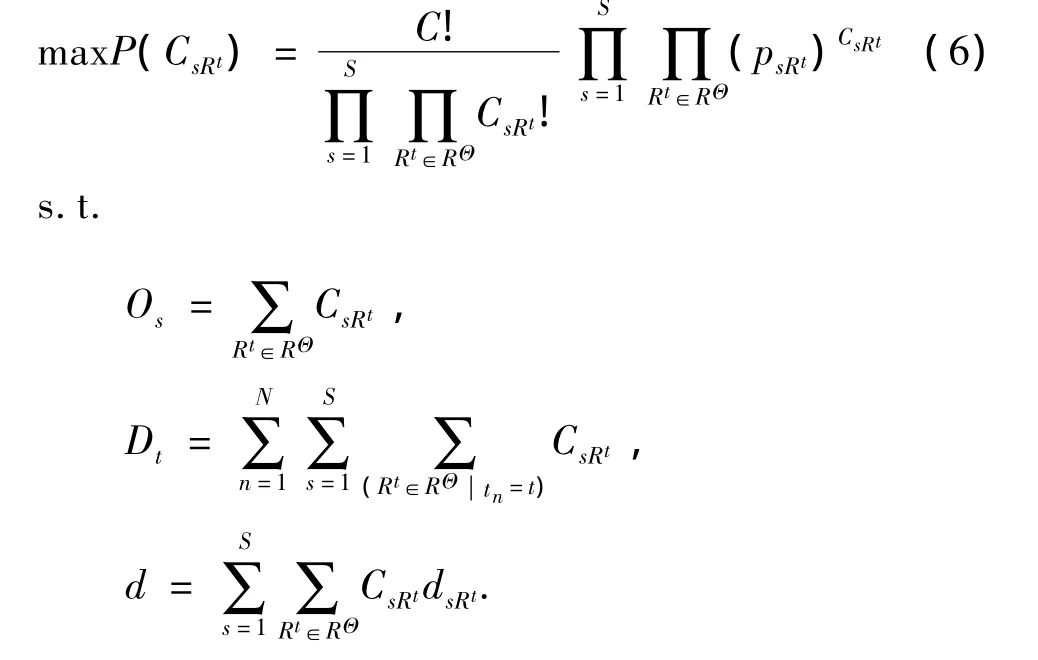
对目标函数取对数,同时运用 Stirling公式N!=NlnN-N,则目标函数转化为

对上述最优化问题,构建Lagrangian公式如下:
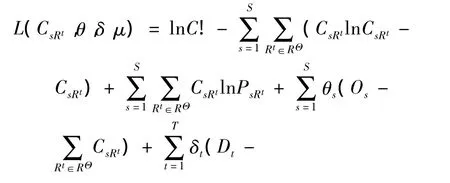
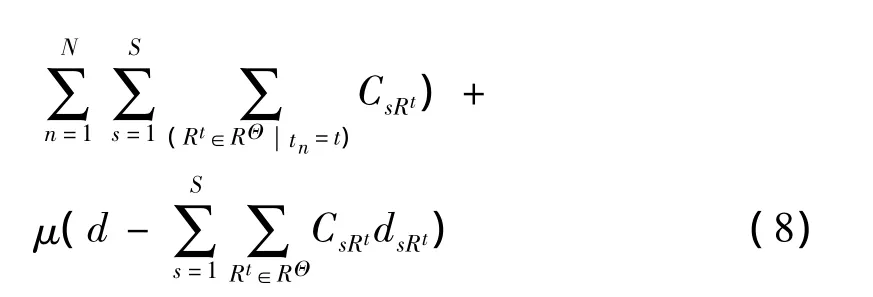
式中,θ、δ和μ为Lagrange算子.根据Karush-Kuhn-Tucker(KKT)条件,对式(8)中CsRt、θ、δ、μ分别求偏导并令其为0,则有
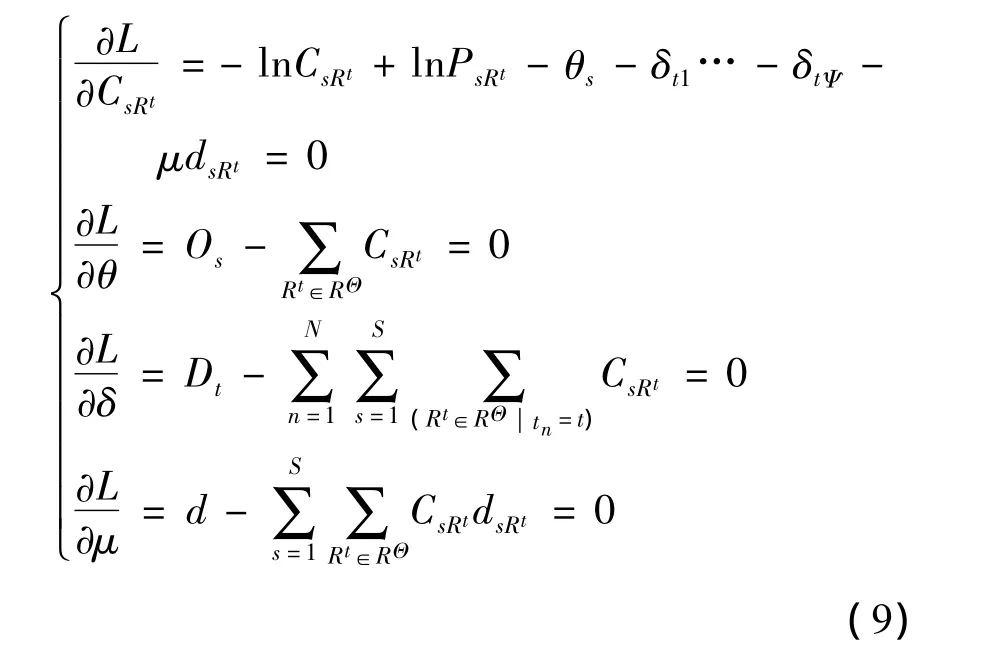
求解上式,得到
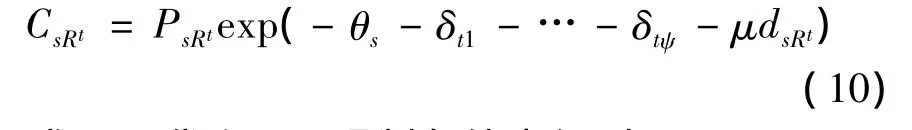
式(10)代入OD限制条件中得到

为简化模型形式,令Gs和Ht为

可以得到

将式(13)代入OD限制条件中,得到
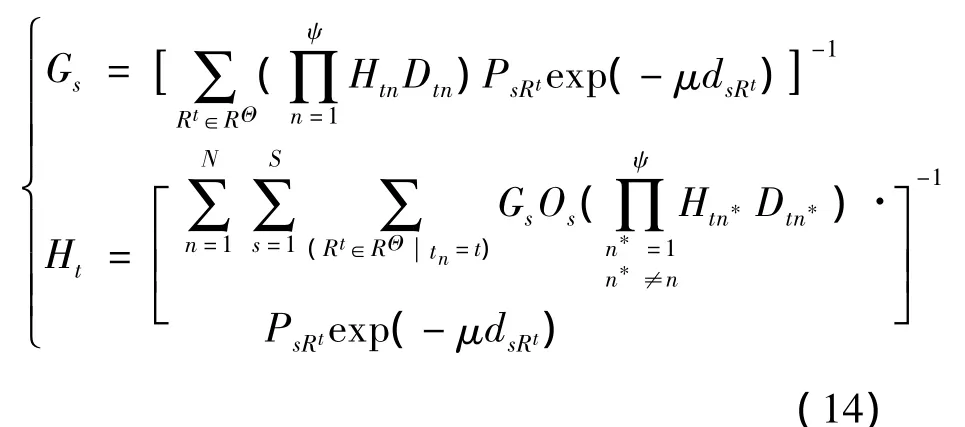
同时将式(13)代入多模式网络下出行链距离限制条件中,得到
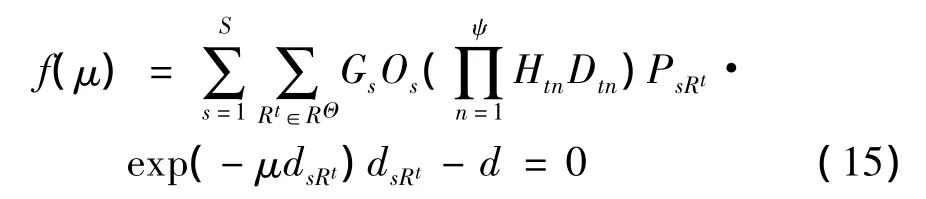
2.2 参数估计
模型中,在给定的研究区域内,交通小区出行发生量Os、到达小区的出行链数量Dt和多模式网络下出行总距离d均为已知条件,而参数Gs、Ht、μ为模型待估参数.参数估计算法步骤如下所示:
步骤1 数值初始化.令μ=μ0,Ht=,=0.
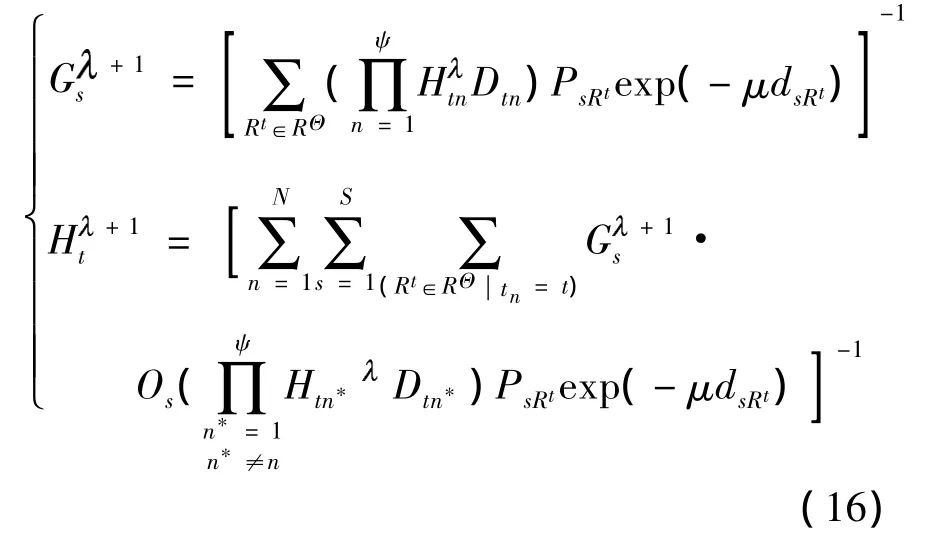
其中,s={1,2,…,S},t={1,2,…,T}.
步骤4 迭代计算μk.令x0=μk,迭代公式如下;

步骤5 令 = +1,返回步骤2.
2.3 先验概率的选择
对最大熵模型的先验概率的选择,文献[13]中假定每种选择为等可能事件,即先验概率PsRt应尽可能定义为相同值.值得注意的是,在出行链模型中,出行链的先验选择概率与出行到达小区数量ψ相关,即有

式中,g(ψ)为出行到达小区数量ψ的方程.在实际的模型操作中,如若缺乏有效的足够先验数据,则Wilson的假设[13]更具实践操作性.
同时,为明确模型计算,模型考虑排除部分出行链,例如,在相同到达小区内连续多次出行的出行链,模型不予考虑,即有若该出行链不应在本模型中予以考虑,则

3 模型应用验证
3.1 模型数据
数据来源于2010年成都市中心城区居民出行调查数据库(由西南交通大学提供),交通网络数据来源于成都市交通地理信息系统(由西南交通大学提供).模型数据的时间点为2010年.
考虑到模型计算的复杂程度,基于随机分层抽样的方法从数据库中随机选取应用样本数据,出行人数为8028人,出行链总数为8028个,包含出行次数为20898人次,出行链的最大到达小区数量为3 (即ψ≤3).
模型范围为成都市中心城区402个交通小区,402个交通小区中各小区的出行发生量和到达量如图3所示,图中括号内的数据为小区数量.
出行链先验概率psRt的选择如2.3节所述,受限于先验数据的不完备,本次模型应用中采用Wilson的模型假设形式.
3.2 模型验证
如2.1节所述,文中模型目标为基于最大熵原理估计计算所有出行链路径sRt的出行量CsRt,因此,为验证模型的有效性,用各个出行链路径的实际值与模型值进行对比.
具体地,表征出行链行为的指标可以分为以下5个:出行链距离,出行链中交通小区间的出行量,出行链到达小区的数量,出行链小区的发生到达量,各类出行链的出行量.
3.2.1 出行链距离对比
根据不同距离范围内的出行链出行者人数,对比模型结果中的出行链的距离dsRt,结果如图4所示.由图4可见,整体而言,模型值与实际值吻合良好.
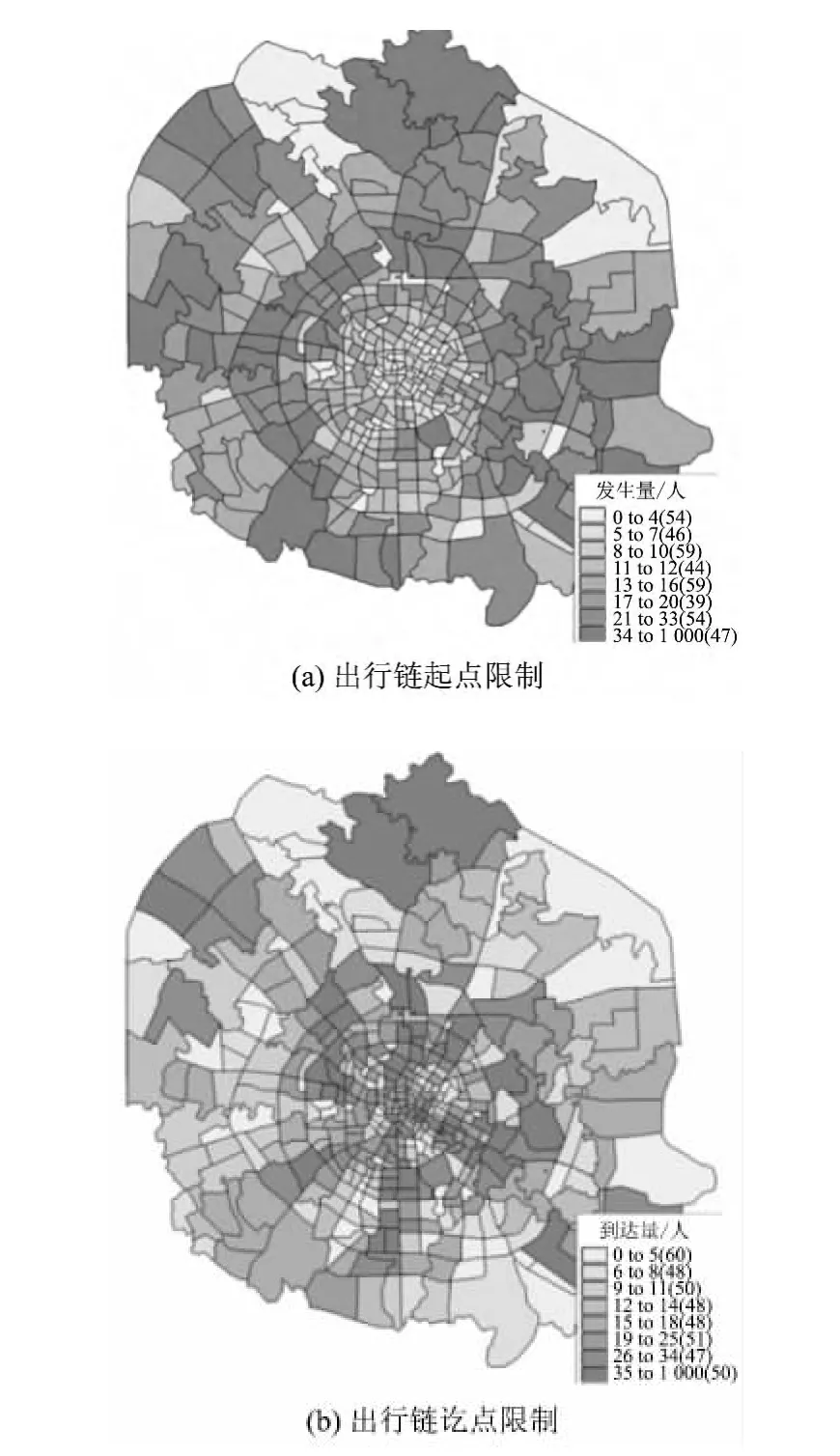
图3 出行链中各交通小区的出行发生量和到达量分布Fig.3 Distribution of trip flow between traffic analysis zones of trip chains
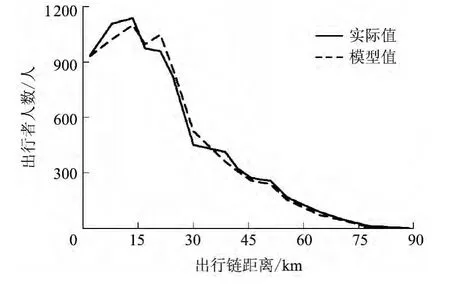
图4 出行链的距离对比Fig.4 Comparison of trip distance of trip chains
3.2.2 出行链中交通小区间的出行量对比
针对出行链中交通小区间的出行量,分以下两类进行对比:出行链中出发小区与到达小区之间的出行量对比,出行链到达小区之间的出行量对比.结果如图5所示,散点图中散点的分布越接近对角线则表示模型值与实际值越接近.
由图5可以看出,在两种情况下,模型值与实际值均较为密集地沿对角线分布.同时,值得注意的是,传统的交通分布的最大熵模型仅考虑出行的出发小区与到达小区之间的出行量,而文中出行链模型还计算得到出行链中的到达小区之间的出行量,这是出行链模型的特点.
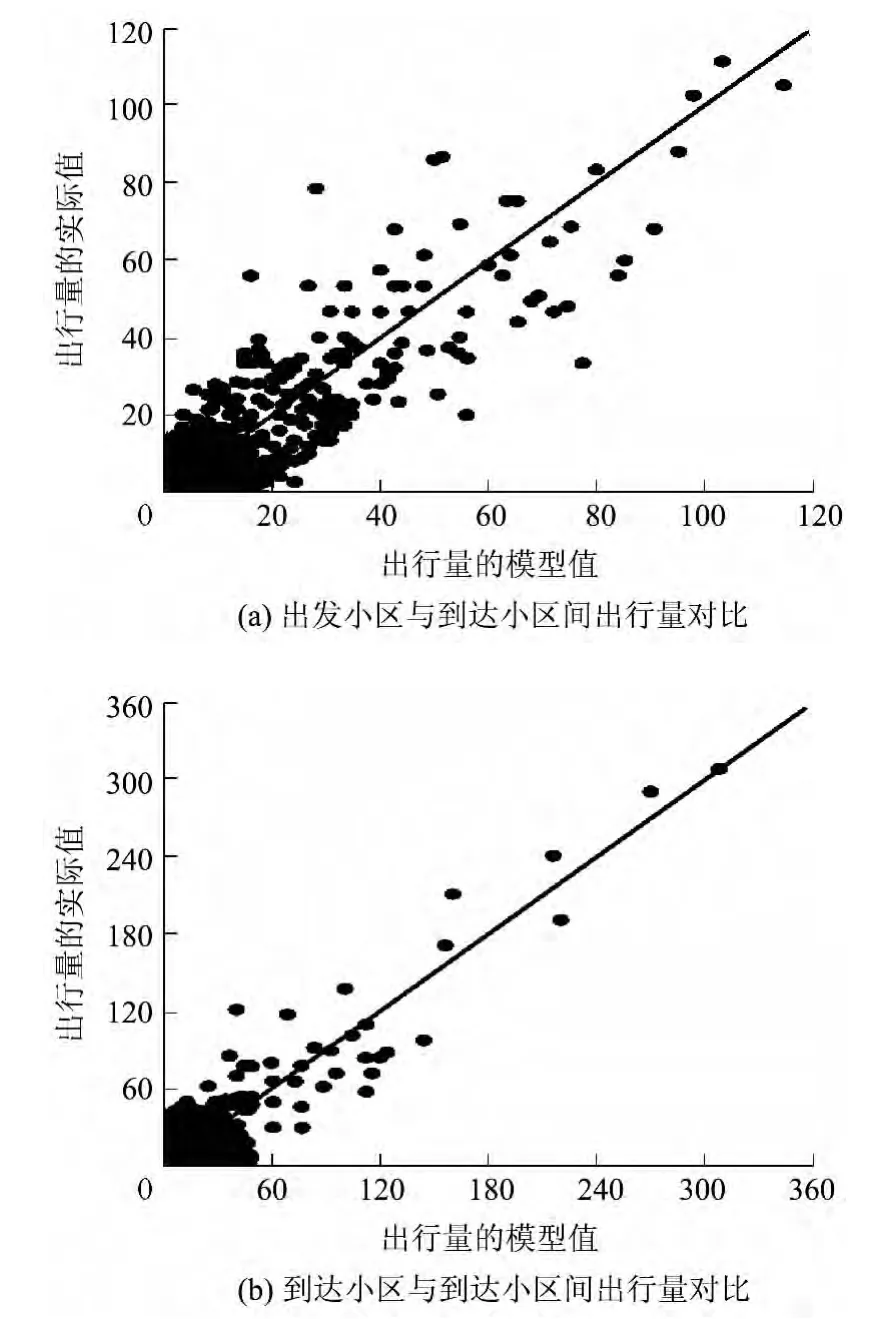
图5 出行链中交通小区间出行量对比Fig.5 Comparison of trip flow between between traffic analysis zones of trip chain
3.2.3 出行链中到达小区的数量对比
出行链中同时包含多个到达小区是出行链的特征,因此,对比模型值与实际值能够表征模型的有效性.不同数量到达小区的出行链数对比如表1.
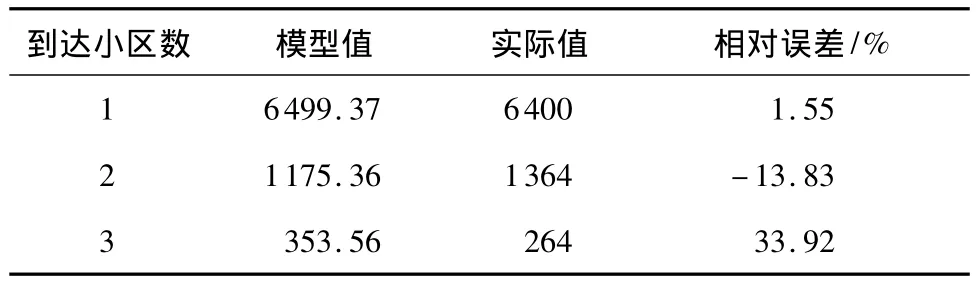
表1 不同数量到达小区的出行链数对比Table 1 Comparison of different arriving between traffic analysis zones of trip chains
由表1可见,随着出行链中到达小区数量的增加,模型的相对误差出现增大的趋势,这与随着到达小区数量的增长模型计算复杂度增加有关.
3.2.4 出行链中小区的发生到达量对比
出行链中小区的到达发生量的对比如图6所示.由图6可见,模型值与实际值接近程度较高.由于模型求解受限于出行链的OD限制条件,因此各个出发小区与到达小区的出行量的模型值与实际值接近程度较好.

图6 出行链中小区的到达发生量对比Fig.6 Comparison of trip flow of different between traffic analysis zones
3.2.5 各类出行链的出行量对比
最后,对各类出行链的出行量CsRt进行对比,这是对模型计算的最终结果的直接对比,如图7所示,3种不同形状的散点符号表示出行链类别,即不同到达小区数量的出行链.从图7可以看出,模型值与实际值接近程度较好.

图7 各类出行链的出行量对比Fig.7 Comparison of trip flow of different trip chains
通过以上5类指标的对比可以看出,出行链行为的最大熵模型具有良好的模型解释能力,能够有效地计算得到各类出行链的出行数量,为全面综合地分析城市交通出行提供了更加有效的模型工具.
4 结语
文中针对已有城市交通出行链行为分析模型的局限性,提出了基于最大熵模型的多模式交通网络下的城市交通出行链行为模型,分析了城市交通出行链的基本概念与简单出行链的可能路径,在此基础上运用最大熵模型,基于OD限制条件与多模式交通网络下的交通距离限制条件,推导构建了出行链行为最大熵模型,并给出了参数估计与先验概率选择方法.将模型应用到成都市中心城区居民出行样本数据中,通过出行链距离、出行链中交通小区间的出行量、出行链到达小区的数量、出行链小区的到达发生量、各类出行链的出行量等5个指标验证了模型结果,模型拟合度均较好,说明了文中方法的有效性.
因样本先验数据的限制,文中模型的先验概率采用了相同值,在进一步的研究中需要注意改进.
[1] 杨扬,姚恩建,岳昊,等.基于支持向量机的出行链活动类别研究[J].交通运输系统工程与信息,2010,10 (6):70-75.Yang Yang,Yao En-jian,Yue Hao,et.al.Trip chain’s activity type recognition based on support vector machine[J].Journal of Transportation System Engineering and Information Technology,2010,10(6):70-75.
[2] Dilum D,Takayuki M.Household travel behavior in developing countries:nested logit model of vehicle ownership,mode choice,and trip chaining[J].Transportation Research Record,2002,1805:45-52.
[3] 褚浩然,郑猛,杨晓光,等.出行链特征指标的提出及应用研究[J].城市交通,2006,4(2):64-67.Chu Hao-ran,Zheng Meng,Yang Xiao-guang,et al.A study on trip-chain indices and their application[J].Urban Transport of China,2006,4(2):64-67.
[4] 赵丹,邵春福,岳昊.多方式诱导信息对通勤者出行链的动态影响模型[J].西南交通大学学报,2013 48 (2):368-375.Zhao Dan,Shao Chun-fu,Yue Hao.Modeling the dynamic impacts of mutil-modal guidance information on commuters’trip chain[J].Journal of Southwest Jiaotong University,2013 48(2):368-375.
[5] 杨敏,王炜,陈学武,等.工作者通勤出行活动模式的选择行为[J].西南交通大学学报,2009,44(2):274-279.Yang Min,Wang Wei,Chen Xue-wu,et.al.Activity pattern choice of work commuting trip by workers[J].Journal of Southwest Jiaotong University,2009,44(2):274-279.
[6] Alder T,Ben-Akiva M.A theoretical and empirical model of trip chaining behavior[J].Transportation Research Part B,1979,13:243-257.
[7] Jenelius E,Mattsson L,Levinson D.Traveler delay costs and value of time of trip chains,flexible activity scheduling and information[J].Transportation Research Part B,2011,45(5):789-807.
[8] Jenelius E.The value of travel time variability with tip chains,flexible scheduling and correlated travel times[J].Transportation Research Part B,2012,46(6):762-780.
[9] Sasaki T.Estimation of person trip patterns through Markov chains[J].Traffic Flow and Transportation,1971,4(11): 119-130.
[10] Lerman S R.The use of disaggregate choice models in semi-Markov process models of trip chaining behavior[J].Transportation Science,1979,13:213-291.
[11] Bowman J,Ben-Akiva M.Activity based disaggregate travel demand model system with daily activity schedules[J].Transportation Research Part A,2000,35:1-28.
[12] 隽志才,李志瑶,宗芳.基于活动链的出行需求预测方法综述[J].公路交通科技,2005,22(6):108-113.Juan Zhi-cai,Li Zhi-yao,Zong Fang.A review of activitybased travel demand forecasting method[J].Journal of Highway and Transportation Research and Development,2005,22(6):108-113.
[13] Wilson A G.A statistical theory of spatial distribution models[J].Transportation Research,1967,1(3):253-269.
[14] 邵昀泓,程琳,王炜.最大熵模型在交通分布预测中的应用[J].交通运输系统工程与信息,2005,5(1): 73-77.Shao Yun-hong,Cheng Lin,Wang Wei.Application of entropy-maximizing(EM)model in traffic distribution forecast[J].Journal of Transportation System Engineering and Information Technology,2005,5(1):73-77.
[15] Honma Y,Kurita O,Taguchi A.Spatial interaction model for trip-chaining behavior based on entropy maximizing method[J].Journal of the Operations Society of Japan,2010,53(4):235-254.

