模拟干湿环境对混凝土内水分影响深度的影响*

刘鹏 宋力 余志武

(中南大学土木工程学院∥高速铁路建造技术国家工程试验室，湖南长沙410075)

式中:D0w为混凝土完全干燥时的扩散系数，m2/s; Dw(Θ)为水分在混凝土饱和度为Θ的条件下的扩散系数，m2/s;S0为完全干状态混凝土的吸水率，m/s1/2;φ为混凝土的毛细孔隙率，%;mw为混凝土完全饱水时的质量，kg;md为混凝土完全干燥时的质量，kg;ρw为水的密度，kg/m3;ρc为混凝土完全干燥时的密度，kg/m3;n为回归系数，一般取6～8.

初始含水率均匀分布的混凝土湿润过程中的吸水量与时间平方根理论上成正比［20］，如式(5)所示:

准确预测新建和既有钢筋混凝土结构在氯盐环境下的使用寿命是混凝土耐久性研究的难点.传统研究多基于电化学加速和盐水浸泡的室内加速腐蚀试验，如文献［1-3］中均采用通电试验方法快速测定混凝土中氯离子的渗透性能;文献［4-7］根据环境、载荷和材料等对扩散的影响提出了基于Fick第二定律的修正模型.上述研究成果侧重于侵蚀加速效果和模型分析，且引入了环境中不存在的因素(如电流等)，对实际环境中不同工况条件下混凝土结构内部氯离子侵蚀机理及真实性研究不足;此外，亦缺乏对使用环境和室内加速试验条件下混凝土氯盐侵蚀相关性的探讨.为克服上述传统研究方法的不足，一些研究者尝试开展模拟加速试验［8-15］.模拟加速试验具有主要因素影响一致、试验再现程度和真实性较高等优点，但其相关性具有不确定性——不同方法、装置和环境间缺乏相关性.因研究者基于不同的立足点来考虑参数、方法和侧重点，所获得的试验结果差别较大，最终导致试验结果的可比性差.事实上，研究成果间的分歧主要体现在如何确定模拟加速试验的参数(模拟温度、湿度、干湿时间、循环周期和盐溶液浓度等);其中，关于模拟试验关键参数之一的干湿时间的分歧最大.部分学者对其进行了研究，如李春秋［14］以润湿0.5 d和干燥3.5、7.0、14.0d为条件研究了混凝土内氯盐的侵蚀，采用预估校正法模拟了混凝土内水分的传输及其影响深度，并提出了平衡时间比概念;Sahmaran等［16］采用室温浸泡6 d和100℃下干燥24 h的干湿交替制度研究了硫酸盐侵蚀下混凝土性能的变化;卢振永［17］在喷雾与温湿时间比为15∶15的情况下，以21 h为循环周期进行了室内模拟试验.干湿时间对模拟试验结果的影响，最终以干湿影响深度的形式予以体现，干湿影响深度可通过传感器直接测定，故可通过研究混凝土内的干湿影响深度间接获取干湿时间的影响效果.上述模拟试验因选用的干湿时间和周期不同，导致了混凝土内水分影响深度及水分分布不等，也使得氯盐侵蚀结果无法定量对比.因此，亟需开展模拟环境中混凝土内干湿影响深度的相关研究.

文中在已有研究成果基础上，采用理论推导和试验相结合的方法研究了混凝土表层内水分的传输、分布及其影响深度的规律，并建立了平衡时间比和影响深度模型;此外，还分析了不同的混凝土平衡时间比的求解方法之间的差异，为确定氯盐环境下模拟加速试验的参数提供指导.

1 理论推导

模拟环境中干湿交替条件下混凝土表层内水分的迁移是水分在润湿和干燥两阶段之间的传质过程.本研究基于文献［14］提出的预估-校正格式有限差分法进行混凝土内湿度分布的数值求解.

1.1 混凝土润湿过程中水分的传输机理

所述湿润过程为混凝土表面始终接触液态水，即边界条件为饱和度Θ(x=0，t)=1或边界毛细管压力pc(x=0，t)=0.研究表明，混凝土润湿过程可以饱和度为变量采用式(1)所示的扩散方程进行描述，而其扩散系数可用式(2)所示的指数函数表示［18］;但因扩散系数难以直接测定，多基于混凝土吸水率与扩散系数间显式关系间接获得［19］，如式(3).

式中:D0w为混凝土完全干燥时的扩散系数，m2/s; Dw(Θ)为水分在混凝土饱和度为Θ的条件下的扩散系数，m2/s;S0为完全干状态混凝土的吸水率，m/s1/2;φ为混凝土的毛细孔隙率，%;mw为混凝土完全饱水时的质量，kg;md为混凝土完全干燥时的质量，kg;ρw为水的密度，kg/m3;ρc为混凝土完全干燥时的密度，kg/m3;n为回归系数，一般取6～8.

初始含水率均匀分布的混凝土湿润过程中的吸水量与时间平方根理论上成正比［20］，如式(5)所示:

式中:S为表面吸水率，m/s1/2;V(t)为时间t内单位截面的累计吸水量，m3/m2.

若混凝土内吸水率表达方式在初始非饱和湿润过程中成立，则初始非饱和混凝土吸水率可用式(6)表示［21］:

式中:Θir为混凝土初始饱和度;Θ1和Θ0分别为混凝土饱和与完全干燥时的饱和度，可分别取1和0.

分析上述推导过程可知，若测定相应饱和度下的表面吸水率，则可得混凝土润湿过程中吸水量的变化曲线，从而间接获取各饱和度对应的水分扩散系数.

1.2 混凝土干燥过程中水分的传输机理

干燥过程中水分在混凝土内以汽-液两相传输，其传输亦可采用Fick定律来描述［22］;当前已有研究的分歧主要集中在干燥非稳态过程中内部扩散系数取值方面.文献［3］推荐的干燥过程中混凝土内水分的扩散系数(为S曲线形式)如式(7);所述干燥过程的边界条件为第一类边界条件，如式(9)所示.

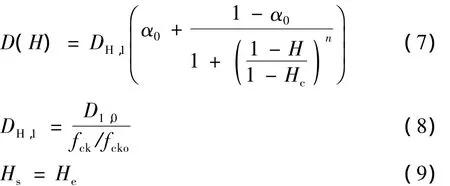
式中:Hs为混凝土内表面相对湿度，%;He为环境相对湿度，%;其他变量符号的意义见文献［3］.

从式(7)和(8)可知，若已知混凝土抗压强度则可估算出相应的混凝土干燥过程的水分扩散系数.

1.3 混凝土内的水分影响深度和平衡时间

研究混凝土内水分变化范围对混凝土结构耐久性估算和使用寿命预测具有实际意义.将混凝土表层含水量变化急剧的深度视为影响深度，且其值为相对量(与饱和度、干湿时间及周期等有关)，如图1中ΔX.若混凝土内初始湿度均匀，则润湿或干燥过程的水分影响深度可采用Fick定律描述，其定解可用式(10)表示;最终影响深度可表示为图1中的ΔX0.

式中:C(x，t)为t时刻、距混凝土表面x处的水分浓度，mol/m3;x为距离表面的深度，m;Cs为混凝土表面的水分浓度，mol/m3;C0为混凝土内部的初始水分浓度，mol/m3;D为水分在混凝土中的扩散系数，m2/s;t为过程持续时间为误差函数，其边界条件为C(0，t)=Cs、C(∞，t)=C0、C(x，0)=C0.

干湿交替过程中混凝土内的水分表现为非均匀分布，故不能直接采用式(10)描述混凝土内水分的分布.将水分影响深度定义为干湿过程中混凝土内某深度处含水率变化超过定值(如1%等)所对应的深度值，相应的水分影响深度如图1中的ΔX，其与ΔX0间的异同将在后文阐释.

图1 不同状态下混凝土内水分的饱和度曲线Fig.1 Water saturation curve in concrete under different conditions

干湿交替过程中混凝土表层内失水与吸水的平衡时间对应着失水与吸水量相等，相应的干燥过程引起的干燥前锋恰能被随后的润湿过程的吸水曲线覆盖，而干燥前锋未到达的深度则不受影响;两个过程的时间比称之为平衡时间比，如式(11)所示.事实上，因混凝土干燥过程的失水量和润湿过程的吸水量与时间的平方根理论上应成正比，故其平衡时间比亦可采用式(12)表示.

式中:ηeq为平衡时间比;td为干燥过程持续时间，s; tw为润湿过程持续时间，s;td-w为试验干湿交替过程周期时间，s;tw-eq、td-eq分别为润湿过程和干燥过程中混凝土表层吸水与失水量相等时的润湿时间及其干燥时间，s;Sw和Sd为表面等效吸水或失水率，m/s1/2.

2 试验

2.1 试验材料与设备

试验所用主要材料有:湖南长沙平塘水泥厂生产的P·O 42.5级硅酸盐水泥;湖南长沙黄腾外加剂厂生产的聚羧酸系列高效减水剂，湖南湘潭电厂产I级粉煤灰，湖南涟源钢铁集团有限公司产S95级矿粉;长沙本地产河砂;长沙本地产石灰岩碎石，连续级配，粒径5～20mm;自来水.试验用混凝土配合比及抗压强度如表1所示.

表1 混凝土配合比及抗压强度Table 1 Mix proportion and compressive strength of concrete

试验用湿度测定仪为湖南省长沙市三智电子科技有限公司生产的SHT10型温湿度传感器，所用环境模拟箱为武汉金亚泰仪器设备有限公司生产多功能环境模拟箱系统.

2.2 试样制作与试验过程

按前述配合比拌制混凝土后浇筑尺寸为150mm× 150mm×150mm和150mm×150mm×400mm的试样.从试样侧面取芯，制备φ100 mm×150 mm的圆柱体;在距混凝土表面不同深度处钻孔，置入温湿度传感器;然后，将其置于杜瓦瓶中并用相同级配混凝土浇筑成型.干燥与润湿试验试样留一侧面，其余面采用环氧树脂密封.润湿试验是将干燥恒重试样暴露面放入塑料盆内预设支架上，加水至液面高出试验浸泡面约2 mm，浸泡不同时间后取出、擦干表面明水后称重;干燥过程在20℃恒温室内进行，将试样放置于支架上并用风扇吹风，定时称重.试验用混凝土试件示意图如图2所示.

图2 混凝土试件示意图(单位:mm)Fig.2 Schematic diagram of the concrete sample(Unit:mm)

3 分析与讨论

3.1 混凝土润湿过程

研究中混凝土内湿度采用饱和度形式表征，为了将相对湿度值转化为相应的饱和度，试验采用不同种类的盐溶液来提供相应的环境相对湿度［14］，从而建立混凝土内饱和度与相对湿度的函数关系.不同相对湿度下混凝土内水分脱附过程中饱和度的实测值及其拟合曲线如图3所示;其中C20、C30、C40、C50混凝土水分脱附过程中饱和度拟合方程分别为y=9.03-8.97/(1+exp((x-1.36)/0.16))(r2= 0.96)、y=9.35-9.28/(1+exp((x-1.41)/ 0.18))(r2=0.95)、y=15.49-14.98/(1+exp((x-1.8)/0.28))(r2=0.92)、y=11.1-11.01/(1+exp ((x-1.63)/0.25))(r2=0.94).试验测得的混凝土表面吸水量及其拟合曲线如图4所示;其中C20、C30、C40、C50混凝土吸水量拟合方程分别为y= 0.143x+0.049(r2=0.97)、y=0.140x+0.128(r2= 0.91)、y=0.081x+0.012(r2=0.92)、y=0.075x+ 0.054(r2=0.90);试验用混凝土内水分初始饱和度约为0.9.

由图3可见，在相同的相对湿度条件下，混凝土的饱和度随强度等级的升高而增大，这是因为高强度等级混凝土内微孔所占比例较高，根据汽-液平衡方程可知其微孔隙可被较多水填充.混凝土饱和度随相对湿度的增加而增大，这是因相对湿度增加使得可填充混凝土内微孔的水量增多造成的.同时，图3表明，指数函数形式的拟合曲线与实测值吻合较好，以下均采用该拟合曲线来换算环境湿度，并将其应用于水分传输模型中.

图3 混凝土内相对湿度与饱和度的关系Fig.3 Relationship between relative humidity and saturation in concrete

图4 混凝土表面吸水量随时间的变化Fig.4 Change of water absorption of concrete surface with time

由图4可见:混凝土表面吸水量随时间的延长而增大，且与时间的平方根成线性关系;混凝土表面吸水量随混凝土强度等级升高而降低，混凝土表面吸水量实测值与拟合曲线吻合较好.基于混凝土表面吸水量拟合曲线的斜率值和上述式(5)，可得出混凝土表面的吸水率S0和完全干燥状态下的水分扩散系数D0w，如表2所示.

由表2可见，S0和D0w均随混凝土强度等级的升高而降低，这是因为混凝土强度越高相应的微观结构越致密，其所含孔隙量降低，相应的毛细孔比例增加，且部分孔隙成为非连通孔隙，使得水分扩散更加困难.

表2 混凝土水分传输参数Table 2 Parameters of water transmission in concrete

3.2 混凝土干燥过程

通常的模拟试验一般采用人工方式加速混凝土的干燥，其干燥时间受环境、湿度梯度、混凝土强度和初始饱和度等因素影响.文中通过混凝土干燥试验来验证混凝土干燥过程规律及其平衡时间比的合理性，施加于混凝土表面的环境湿度对应的混凝土内饱和度约为0.4.干燥过程中混凝土失水量随时间的变化如图5所示，其中C20、C30、C40、C50混凝土表面失水量拟合方程分别为 y=0.0295x+ 0.4017(r2=0.96)、y=0.032x+0.448 7(r2= 0.97)、y=0.0155x+0.2713(r2=0.99)、y=0.0145x+ 0.3077(r2=0.98).

图5 干燥过程中混凝土失水量随时间的变化Fig.5 Change of water loss of concrete with time in drying process

由图5可见:干燥过程中混凝土失水量随时间延长而增加，混凝土强度越低其失水量曲线斜率越大，故失水系数越大;混凝土干燥过程中失水量与时间平方根成线性关系，这表明混凝土干燥过程中的失水量可用扩散方程描述［18］.通过混凝土干燥过程中失水量与时间平方根间的线性拟合可得到相应的失水率——可用来衡量混凝土失水的快慢.

3.3 混凝土平衡时间比及其影响深度

模拟试验中干燥与润湿时间比是试验制度的重要参数之一，获取该值的方法和取值精度是决定模拟试验合理与否的关键.下面对基于式(12)的求解法和混凝土内水分传输模型的数值模拟法(即采用预估-校正格式有限差分法进行混凝土内湿度分布的数值求解法)之间的异同进行分析;试验以试样重量及其内部相对湿度变化为基准，来衡量润湿与干燥平衡时间比.

基于公式(12)求出C20-C50混凝土的平衡时间比分别约为19、21、27和26，而按混凝土内水分传输模型数值模拟法所求相应值分别约为16、18、26和22;两种方式解得的数值大体一致，这表明在无法获取混凝土内水分扩散系数时，可通过简单地测定混凝土表面吸水和失水系数来求解混凝土的平衡时间比.两者间的差异可能是因混凝土表层与内部微观结构不同引起水分传输效果差异造成的.文献［14］给出的混凝土润湿过程吸水率与干燥过程失水率分别为3.75 g/h1/2、0.331 g/h1/2;若基于式(12)可求出其平衡时间比约为128，而基于水分传输模型数值模拟法求得该值约为120，这也间接证明了混凝土平衡时间比法的合理性;至于两者之间的差异可能是因实际混凝土初始湿度与假设值不等、S曲线求解混凝土饱和度时的扩散系数存在误差等因素造成的.尽管基于式(12)求解平衡时间比方法简单、易行，但其不能实时直观地描述混凝土内的水分分布和影响深度等，采用水分传输模型数值模拟法则可弥补上述不足.以下将利用水分传输模型数值模拟法来探讨混凝土干湿交替条件下的水分传输.

文中对不同干湿交替条件下的混凝土内部饱和度进行了数值模拟计算，并通过试验验证其合理性.以混凝土初始饱和度(Θe)为0.8、混凝土表面的环境饱和度为0.4和表2中的参数进行模拟计算，以混凝土试样重量变化为依据来衡量干湿时间;试验实测的干燥平衡时间及其数值模拟曲线如图6所示，其中C20、C30、C40、C50混凝土平衡干燥时间拟合方程分别为y=87x(r2=0.99)、y=100x(r2= 0.99)、y=136x(r2=0.99)、y=157x(r2=0.99).

图6 混凝土的润湿时间与平衡干燥时间Fig.6 Wetting time and equilibrium drying time of concrete

由图6可见，特定条件下混凝土的平衡时间比为定值且不受限于干湿周期长短，平衡时间比随混凝土强度等级升高而增大，混凝土平衡时间比实测值与数值模拟曲线基本一致.为更好地研究混凝土平衡时间比的变化规律，以下分别探讨混凝土初始饱和度、混凝土表面的环境饱和度和水灰比(W/C)对平衡时间比的影响.混凝土表面的环境饱和度对混凝土平衡时间比的影响如图7所示，其中:混凝土初始饱和度为0.9时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=3.2exp(x/0.305)+3.63、y= 0.93exp(x/0.187)+10.09、y=0.094exp(x/0.109)+ 17.73、y=1.54exp(x/0.208)+15.47;混凝土初始饱和度为0.8时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=1.14exp(x/0.149)+25.69、y=0.8exp(x/0.137)+33.02、y=0.397exp(x/0.112)+ 49.1、y=0.376exp(x/0.108)+58.6;混凝土初始饱和度为0.7时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=2.304exp(x/0.135)+ 40.66、y=1.84exp(x/0.122)+57.3、y=159.78exp (x/0.552)-90.5、y=198.5exp(x/0.623)-103.3.

由图7可知，混凝土平衡时间比与混凝土表面的环境饱和度之间成指数函数关系.若混凝土初始饱和度相同，平衡时间比则随混凝土表面的环境饱和度和混凝土强度增加而增大;若混凝土强度等级相同，平衡时间比则随混凝土初始饱和度降低而增大，随混凝土表面的环境饱和度减小而降低;若混凝土表面的环境饱和度相同，平衡时间比则随混凝土强度等级增加而增大，随混凝土初始饱和度增加而降低.这是因为混凝土强度等级越高其微观结构越致密，所含孔隙率、连通孔数量和大孔比例越少，体系的水分扩散通道和水分扩散系数较小;混凝土表面的环境饱和度越低，则混凝土内外饱和度梯度也越大——水分扩散驱动力较强.

水灰比对混凝土平衡时间比的影响如图8所示，其中:混凝土表面的环境饱和度为0.6时，初始饱和度为0.9、0.8、0.7的混凝土的干湿平衡时间比拟合方程分别为y=1 783exp(-x/0.151)+185、y=41513exp(-x/0.048)+88.5、y=127.6exp(-x/ 0.198)+16.4;混凝土表面的环境饱和度为0.4时，初始饱和度为0.9、0.8、0.7的混凝土的干湿平衡时间比拟合方程分别为y=7 434exp(-x/0.047)+ 15.8、y=14 086exp(-x/0.051)+42.9、y= 22275exp(-x/0.066)+70.8;混凝土表面的环境饱和度为0.2时，初始饱和度为0.9、0.8、0.7的混凝土的干湿平衡时间比拟合方程分别为y= 128.6exp(-x/0.135)+6.76、y=2819.4exp(-x/ 0.069)+28.5、y=18657exp(-x/0.062)+43.9.

图7 混凝土表面的环境饱和度对平衡时间比的影响Fig.7 Influence of environment saturation around concrete surface on equilibrium time ratio

由图8可知，水灰比对混凝土平衡时间比的影响规律与混凝土表面的环境饱和度对混凝土平衡时间比的影响规律相似，影响规律亦可采用指数函数描述;平衡时间比随水灰比增加而降低，随混凝土初始饱和度降低而增加，亦随施加于混凝土表面环境饱和度降低而减小.从图8还可知，若混凝土表面的环境饱和度相同，则混凝土初始饱和度越低，水灰比对平衡时间比影响越显著.

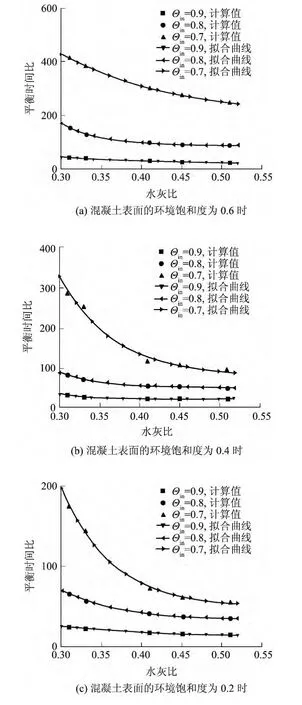
图8 水灰比对混凝土平衡时间比的影响Fig.8 Influence of water-to-cement ratio on equilibrium time ratio of concrete

混凝土初始饱和度对平衡时间比的影响规律如图9所示，其中:混凝土表面的环境饱和度为0.6时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=158290exp(-x/0.109)-15.8、y= 1.19×106exp(-x/0.0845)+4.82、y=465524exp (-x/0.099)-11.2、y=172287exp(-x/0.118)-38.8;混凝土表面的环境饱和度为0.4时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=3 998exp(-x/0.195)-24.1、y=1.06× 106exp(-x/0.156)-15.4、y=2.93×106exp(-x/ 0.074)+4.6、y=4.18×106exp(-x/0.072)+ 10.6;混凝土表面的环境饱和度为0.2时，C20、C30、C40、C50混凝土干湿平衡时间比拟合方程分别为y=489.7exp(-x/1.316)-236.9、y=853exp (-x/0.373)-63.9、y=1.15×105exp(-x/0.105)-2.6、y=1.66×105exp(-x/0.102)-4.4.

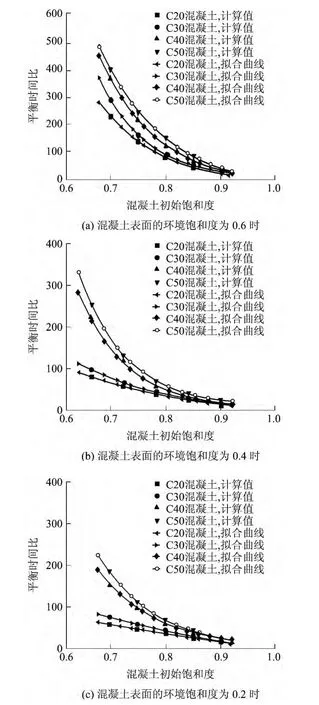
图9 混凝土初始饱和度对平衡时间比的影响Fig.9 Influence of initial saturation in concrete on equilibrium time ratio

由图9可见:混凝土初始饱和度对平衡时间比影响显著，随混凝土初始饱和度增加而减小;两者间的函数关系也可用指数函数描述;混凝土表面的环境饱和度相同时，平衡时间比随混凝土强度等级的升高而增大;混凝土强度和初始饱和度相同时，平衡时间比随混凝土表面的环境饱和度降低而减小.

除采用试算法求解混凝土干湿交替过程的平衡时间比，文中还以混凝土表面的环境饱和度为0.4和混凝土初始饱和度为1.0、0.8为例，探讨了干湿时间比对混凝土内水分湿度分布的影响规律;干湿时间比对混凝土内水分饱和度分布的影响规律如图10所示，其值基于混凝土内水分传输模型数值模拟法求得.图中所述润湿过程和干燥过程各1次即为1周期干湿循环过程(简称1周期)，依次类推.由图10(a)可见，对于初始处于饱和状态的混凝土，若(即润湿时间大于干燥失水所需时间)，则干燥前锋未影响区域将维持饱和状态——效果与一致，且影响深度将由干燥时间决定;若(即润湿时间小于干燥失水所需时间)，则润湿前锋未能到达上次干燥前锋产生的影响深度，故干燥前锋将逐渐深入混凝土内部且降低混凝土饱和度.对于初始处于非饱和状态的混凝土，若(即润湿时间等于燥失水所需时间)，则混凝土内饱和度曲线呈准稳定状态——水分影响深度趋于定值，如图10(b)所示;若，则润湿前锋将逐渐深入混凝土内部，且润湿过程将使得混凝土内部饱和度增加，如图10(c)所示;若，则干燥前锋将逐渐深入混凝土内部，且干燥过程将降低混凝土表层饱和度，如图10(d)所示.简言之，若干湿时间比与平衡时间比不等，则最终将改变原有混凝土内的初始饱和度状态，并将不断持续进行，直至达到与干燥/润湿时间比相匹配的混凝土新的饱和度准稳态，相应的时间比将成为新稳态下混凝土的平衡时间比.从图10中还可知，干湿交替过程持续一定时间时，混凝土内水分影响深度将趋于定值，这可能与集肤效应有关，与热集肤层厚度相似，文中称其为湿集肤层厚度.从上述研究可知，水分影响深度主要与混凝土强度等级、混凝土初始饱和度、混凝土表面的环境饱和度、干湿循环周期和平衡时间比等因素有关.为探讨这些因素相互间的内在联系，在Θin=0.8、Θe=0.2，0.4，0.6的条件下，探讨了混凝土强度等级和混凝土表面的环境饱和度对混凝土内水分影响深度的影响.恒时间比条件下混凝土内水分影响深度与润湿时间之间的关系如图11所示，其中:Θe为0.2、0.4、0.6时影响深度拟合方程分别为 y= 17.66x+0.31、y=19.36x+0.54、y=25.83x+ 0.01;C20、C30、C40、C50混凝土影响深度的拟合方程分别为y=20.32x-0.25、y=18.63x+0.52.y= 18.93x+0.16、y=18.36x+0.03.

图10 干湿时间比对混凝土内水分饱和度分布的影响Fig.10 Influence of drying-wetting time ratio on saturation distribution in concrete

图11 润湿时间对混凝土内水分影响深度的影响Fig.11 Influence of wetting time on water influence depth in concrete

由图11可见:在混凝土平衡时间比制度下，混凝土内水分的影响深度与润湿时间的平方根成线性关系;混凝土内水分的影响深度随润湿时间延长而增加，这是因时间越长进入混凝土内部的水分越多造成的;若混凝土内初始饱和度相同，则影响深度随混凝土表面的环境饱和度增加而降低，这是因混凝土与环境间湿度梯度驱动力降低引起的;若混凝土内初始饱和度和施加于其表面的环境饱和度相同，则影响深度随混凝土强度等级的升高而降低，这是因混凝土强度等级越高其致密性越好，相应的水分扩散系数越低.

4 结论

通过模拟干湿环境对混凝土内水分影响深度和混凝土平衡时间比的影响研究，得出以下主要结论:

(1)模拟干湿环境和混凝土自身特性对混凝土平衡时间比影响显著.数值模拟结果表明，混凝土水灰比、混凝土内初始饱和度及表面的环境饱和度与混凝土平衡时间比间存在指数函数关系;平衡时间比随混凝土表面的环境饱和度和混凝土强度等级的增加而增大，随混凝土内初始饱和度增加而降低.基于混凝土表层吸水和失水系数比值法(式(12))求出的混凝土平衡时间比与按混凝土内水分传输模型数值模拟法所求值大体一致.

(2)特定模拟环境条件下，混凝土存在确定的干湿平衡时间比与之相对应.干湿时间比与平衡时间比相等时，混凝土内饱和度曲线呈现为准稳定状态;反之，若干湿时间比与平衡时间比不等，则最终效果为改变原有混凝土内初始饱和度状态，并将不断持续进行，直至构筑出与干燥/润湿时间比相匹配的混凝土新的饱和度准稳态，相应的时间比将成为新稳态下混凝土的平衡时间比.

(3)混凝土内水分的影响深度主要与混凝土强度等级、混凝土初始饱和度、混凝土表面的环境饱和度、干湿循环周期和平衡时间比等因素有关，且与润湿时间平方根成线性关系.

［1］ Tang Lu-ping.Concentration dependence of diffusion and migration of chloride ions(Part 1):theoretical considerations［J］.Cement and Concrete Research，1999，29(9): 1463-1468.

［2］ Magge M，Helland S.Service life prediction of existing concrete structures exposed to marine encironment［J］. ACI Materials Journal，1996，93(6):602-608.

［3］ CEB-FIP Model Code 1990，Design Code［S］.

［4］ 余红发，孙伟.混凝土氯离子扩散理论模型［J］.东南大学学报，2006，36(增刊):68-73. Yu Hong-fa，Sun Wei.Model research on chlorine ion diffusion in concretes［J］.Journal of Southeast University，2006，36(Suppl):68-73.

［5］ 金伟良，张奕，赵羽习.氯离子在火灾后混凝土中的扩散模型［J］.建筑材料学报，2005，8(2):145-149. Jin Wei-liang，Zhang Yi，Zhao Yu-xi.Diffusion mechanics of chloride ions in concrete after fire［J］.Journal of Building Materials，2005，8(2):145-149.

［6］ Clear K C.Time to corrosion of reinforcing steel in con-crete slabs［J］.Journal of the Transportation Research Board，1974，3(3):16-24.

［7］ Gao Jian-ming，Yu Zhen-xin，Song Lu-guang，et al.Durability of concrete exposed to sulfate attack under flexural loading and drying-wetting cycles［J］.Construction and Building Materials，2012，33(5):1-6.

［8］ Konin A，Francois R，Arliguie G.Penetration of chloride in relation to the microcracking state into reinforced ordinary and high strength concrete［J］.Material and Structures，1998，31(1):310-316.

［9］ Castro P，Veleva L，Balancan M.Corrosion of reinforced concrete in a topical marine environment and in accelerated tests［J］.Construction and Building Materials，1997，11(2):75-81.

［10］ Swamy R N，Tanikawa S.An external surface coating to predict concrete and steel from aggressive environments［J］.Materials and Structures，1993，26(10):465-478.

［11］ 刘志勇.基于环境的海工混凝土耐久性试验与寿命预测方法研究［D］.南京:东南大学材料科学与工程学院，2007.

［12］ 姬永生.自然与人工气候环境下钢筋混凝土退化过程的相关性研究［D］.徐州:中国矿业大学土木工程学院，2007.

［13］ Li Chun-qiu，LiKe-fei，Chen Zhao-yuan.Numerical analysis of moisture Influential depth in concrete and Its application in durability design［J］.Tsinghua Science and Technology，2008，13(S1):7-12.

［14］ 李春秋.干湿交替下表层混凝土中水分与离子传输过程研究［D］.北京:清华大学土木水利学院，2009.

［15］ Li Chun-qiu，Li Ke-fei，Chen Zhao-yuan.Influential depth of moisture transport in concrete subject to dryingwetting cycles［J］.Cement and Concrete Composites，2009，31(10):693-698.

［16］ Sahmaran M，Erdem T K，Yaman I O.Sulfate resistance of plain and blended cements exposed to wetting-drying and heating-cooling environments［J］.Construction and Building Materials，2007，21(8):1771-1778.

［17］ 卢振永.氯盐腐蚀环境的人工模拟试验方法［D］.杭州:浙江大学土木工程学院，2007.

［18］ Gummerson R，Hall C，Hoff W.Unsaturated water flow within porous materials observed by NMR imaging［J］. Natrure，1979，281(5726):56-57.

［19］ Lockington D，Parlange J，Dux P.Sorptivity and the estimation of water penetration into unsaturated concrete［J］.Materials and Structure，1999，32(5):342-347.

［20］ Hall C.Water sorptivity of mortars and concretes:a review［J］.Magazine Concrete Researcher，1989，41 (147):51-61.

［21］ Hall C，Hoff W D，Skeldon M.The sorptivity of brick: dependence on the initial water content［J］.Journal of Physics D:Applied Physics，1983，16(10):1875-1880.

［22］ Carslaw，Jaeger.Conduction of heat in solids［M］.Oxford:Clarendon Press，1959.