无限小变换下对谐和坐标条件的思考
王备战,尚晓星,韩胜强,王银平
(1.焦作师范高等专科学校 理工学院,河南 焦作 454000,2.焦作市第31中学,河南 焦作 454000)
1 谐和坐标条件研究现状
2 论证过程
在弱的引力场中,度规张量写成平度规与一个小量和的形式时,Ricci张量由如下方程给出[5]:
其中,g(0)lm为平度规的逆变度规张量;hik为实际度规关于平度规的修正小量.由题设中的谐和坐标条件,消去后三项,得到:
由上式可知,真空中的引力场方程为[5]:

这便是真空中的引力场方程所满足的达朗贝尔波动方程.
打开终端,进入项目工程文件,输入Ionic封装的Cordova打包命令先添加iOS平台,命令为“ionic cordova platform add ios”,再输入创建命令“ionic cordova build ios”即可生成可以运行在iOS平台上的工程项目,iOS工程项目在该项目工程目录下的“platforms”文件夹下的“iOS”文件夹内,再用Xcode工具运行工程即可完成iOS平台的打包流程。
首先,建立一个无穷小坐标变换:
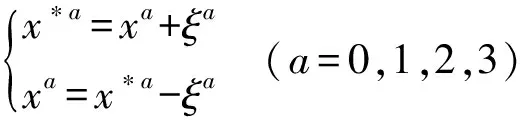
(1)
其中,ξa是与hik同量级的小量.
写出度规张量在方程组(1)下的坐标变换式并略去方程中比的高阶小量后,得:
(2)
其中,εμv表平度规
或者将方程(2)改写为:
(3)

(4)
故有:
(5)
由方程(4)得到如下方程组:
(6)
由此可以得到下式:
h+ψ=0
(7)
把方程组(6)代入到方程(5)得:
(8)
整理方程(3)成如下形式:
(9)
由方程(7)、(8)、(9)得:
(10)
建立如下方程组:
(11)
可得:

(12)
由于坐标变换是无限小变换,方程(12)可以近似表述为:
(13)
又由于:
λμ=ερσ∂σψμρ
(14)
方程(14)代入到方程(13)并整理得:
故有:

3 结论
谐和坐标条件在任意无限小的坐标变换下,坐标变换小量满足谐和方程.谐和坐标条件与谐和方程之间存在关系支持黎曼时空优越坐标系存在的观点.但还需要更直接的证据来证实.
从论证过程可以看出:在进行新的坐标变换时,变换前后的度规张量都应该是场方程的解,当新的坐标变换应用到谐和坐标条件时使得无限小变换的小量满足谐和方程.
[参考文献]
[1] 刘辽,赵峥.广义相对论(第二版)[M].北京:高等教育出版社,2004.
[2] 段一士,张敬业.关于广义相对论中福克的谐和坐标条件[J].物理学报.1962 ,18(4):211-217.
[3] 福克 B.A.时间、空间和引力的理论[M].周培源,等译.北京:科学出版社,1965:244-246
[4] 周培源.论Einstein引力理论中坐标的物理意义和场方程的解[J].中国科学A,1982(4):334-345.
[5] E.M.栗弗席兹,L.D.朗道.场论[M].任朗,袁炳楠译.北京:人民教育出版社,1978.

