复变函数中未定式极限的求解*
王 磊,侯 黎
(1.焦作师范高等专科学校 应用数学研究所,河南 焦作 454000; 2.河南理工大学 数学与信息科学学院,河南 焦作 454100)
0 引言
在实分析中,如数学分析,高等数学等相关课程中,未定式的极限是可以利用洛必达法则求解的,洛必达法则是利用拉格朗日中值定理证明得出的.但在复分析的复变函数课程里,微分中值定理是不成立的,例如复指数函数ez就是一个周期函数,但是其导数恒不为0,明显罗尔中值定理不成立,罗尔的后续定理如拉格朗日中值定理,柯西中值定理随之亦不成立,本文进行了详细的阐述.
另外,在z→z0时,分式未定式极限的求解中,我们会注意到z0点往往就是分子,分母的零点或者极点,而复变函数课程中对零点的阶,极点的阶是有详细研究的,本文顺势给出了阶的比较法求解未定式极限.
1 未定式型的极限


其实,上述形式的洛必达法则还是可以改进的,因为复变函数中解析性是非常好的,如无穷可微,级数展开等等,本文给出如下形式的洛必达法则:
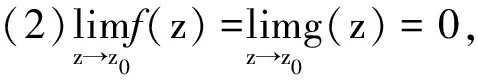

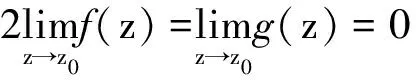
综上,可知级数展式为:f(z)=cp(z-z0)p+cp+1(z-z0)p+1+cp+2(z-z0)p+2+…
g(z)=bq(z-z0)q+bq+1(z-z0)q+1+bq+2(z-z0)q+2+… 其中cp,bq≠0

在上述极限求解中,只需要分子,分母同除以min{p,q}次即可得出结论.
又由幂级数和的解析性,展式两侧可逐项求导,即有:
f′(z)=pcp(z-z0)p-1+(p+1)cp+1(z-z0)p+(p+2)cp+2(z-z0)p+1+…
g′(z)=qbq(z-z0)q-1+(q+1)bq+1(z-z0)q+(q+2)bq+2(z-z0)q+1+…
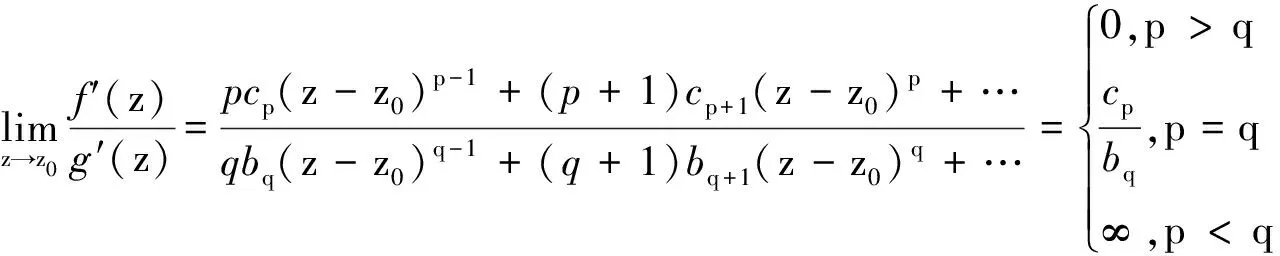


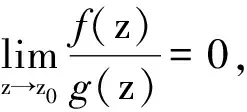
证明:由零点的阶性质[1],可得f(z)=(z-z0)mφ(z),g(z)=(z-z0)nψ(z),
其中φ(z),ψ(z)在点z0解析且φ(z0)≠0,ψ(z0)≠0
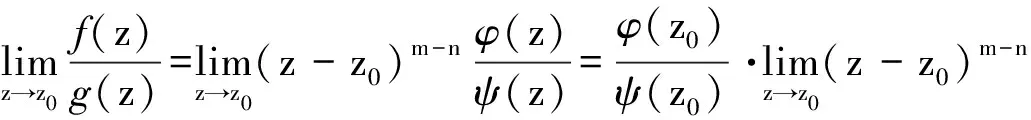


而m=n时,关注参考文献[1]中第167页中阶的性质证明,可知

注:在参考文献3中,也有相关结论,其中只给出了m=m时的情况,不够全面.
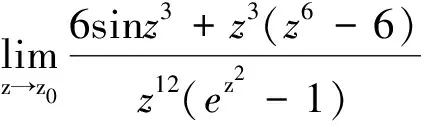
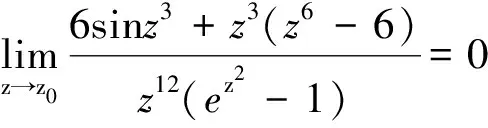
这个例题如果通过定理1.1去解决,是需要连续用14次洛必达法则的,计算量非常大.
2 未定式型的极限
对于z→z0时,分子,分母同趋于∞的情况也有相似的结论,证明同样是利用双边幂级数展开,此时点z0必为分子,分母的极点,考虑重心在负幂部分即可,此时负幂部分都是有限项,在这里不详细论证了,直接给出如下结论:
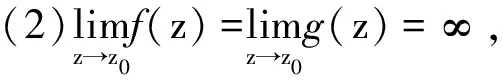
定理2.2 若点z0是解析函数f(z)的m阶极点,是解析函数g(z)的n阶极点,
3 z→∞时,未定式和型的极限

4 结语
我们主要讨论的是分式未定式极限的求解问题,至于其余类型的未定式如:0·∞型,00型,1∞型,∞0型,我们都可以通过同除法,幂指型变形法转化为分式未定式,再用本文中的结论进行求解.
[参考文献]
[1] 钟玉泉. 复变函数论(第四版)[M].北京:高等教育出版社,2013,8:167-168.
[2] 高颖. 洛必达法则在复变函数极限中的应用[J].科技致富向导,2010(29):81-82.
[3] 李景和. 复变函数中的一个有用的法则[J]. 河北工业大学成人教育学院学报,2004(4):1-2.

