Synchronization of High-order Discrete-time Linear Complex Networks with Time-varying Delays

Hai-Long Li，Jian-Xiang Xi，Yao-Qing Cao，Duo-Sheng Wu

(Xi’an Research Institute of High Technology，Xi’an 710025，China)

1 Introduction

Synchronization of complex networks has attracted considerable attention from scientific communities in the past few years. Klinshov and Nekorkin［1］investigated synchronization problems of oscillator networks with time delays，where it was supposed that time delays are constant.In Ref.［2］，synchronizablity of small-world dynamical networks was discussed.A time-varying dynamical network model was constructed in Ref.［3］，where several synchronization criteria were proposed.Chen and Lü［4］proposed finite-time synchronization protocols and presented sufficient conditions for finite-time synchronization.Olfati-Saber and Murray［5］addressed synchronization problems of complex networks with both switching topologies and time-delays.Each agent in complex networks was modeled as a first-order system［1－5］.Because the firstorder systems have a special structure， the synchronization problems for first-order complex networks can be simplified.

However，many complex networks are of high order and cannot be modeled as first-order ones.Xiao and Wang firstly discussed synchronization analysis and design problems for high-order complex networks in Ref.［6］，where it was required that synchronization functions are time-invariant.In Ref.［7］，high-order linear time-invariant(LTI)complex networks with switching undirected topologies were dealt with and sufficient conditions for synchronization were shown.Li et al.［8］proposed dynamic output feedback synchronization protocols with specific structures.Output synchronization problems were dealt with in Refs.［9－11］.In many practical complex networks，time delays were often encountered，but the influences of time delays on synchronization were not considered in Refs.［6－11］.Continuous-time linear complex networks with time delays were dealt with，but its approaches are no longer valid for discrete-time cases since the structures of the two types of complex networks are different［12］.Moreover，it was supposed that all state information is available to construct synchronization protocols［12］.

In the current paper，a general dynamic output feedback synchronization protocol is proposed to deal with synchronization analysis problems of high-order discrete-time LTI complex networks.By the state space decomposition，a necessary and sufficient condition for synchronization is given，but it is not a direct criterion for synchronization.Furthermore，by linear matrix inequality(LMI)techniques，sufficient conditions for synchronization are presented， which are only associated with the second smalland maximum eigenvalues of the Laplacian matrix of the associated communication topology and can guarantee the scalability of networks since the dimensions of all variables are independent of the number of agents.Moreover，an explicit expression of the synchronization function is given，which is only associated with initial states of all agents but is independent of communication topologies.

2 Problem Description

Consider a complex network with N agents which inter-act with each other via local communications.A connected undirected graph G is used to describe the communication topology of the complex network.For i，j∈{1，2，…，N}，the node viin G represents agent i，the edge(vi，vj)corresponds to the information channel from agent i to agent j，and the adjacency element wjidenotes the interaction strength of the channel(vi，vj).

Let xi(k)∈Rd(i∈{1，2，…，N})denote the state ofagent i，which are required to achieve synchronization，then the dynamics of agent i can be described by

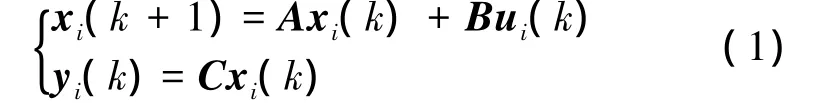
where A∈Rd×d，B∈Rd×m，C∈Rq×d，d is a positive integer，ui(k)is the control input and yi(k)is the measured output. The following dynamic output feedback synchronization protocol is applied:

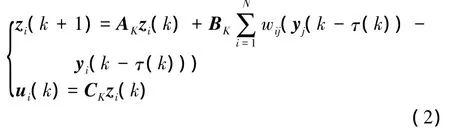
where i，j=1，2，…，N，zi(k)∈Rldenotes the state of the protocol;l is a positive integer and denotes the dimension of the state of the protocol，zi(k)=0(k＜0);AK，BKand CKare constant gain matrices with appropriate dimensions.It is assumed that the timevarying delay τ(k)satisfies 1≤τ(k)≤¯τ with¯τ≥1 denoting the upper bound of τ(k).

Let vi(k)=［xTi(k)， zΤi(k)］T(i=1，2，…，N) andthen network(1)with protocol(2)can be described by

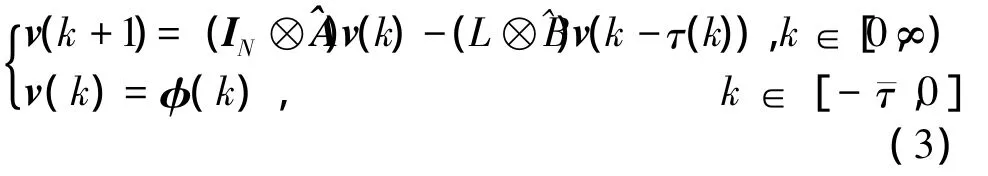
where L is the Laplacian matrix of G;φ(k)is a vectorvalued function and

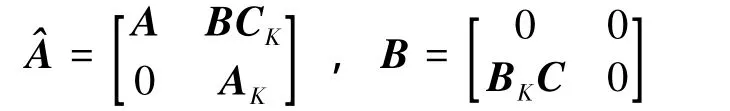
Definition 1 Network(3)is said to achieve synchronization if there exists a vector-valued function c(k)such that，where c(k)is called a synchronization function.

The following two synchronization problems of network(3)are investigated:1)For given AK，BKand CK，under what conditions network(3)achieves synchronization;2) how to determine the synchronization function if network (3)achieves synchronization.

In the current paper，0 is used to denote zero matrices of any size with zero vectors and zero number as special cases.In symmetric block matrices，an asterisk(*)stands for a symmetric term.Let diag{Δ1，Δ2，…，Δn}denote a diagonal block matrix with diagonal blocks Δ1，Δ2，…，Δnrespectively.Moreover，basic concepts and results about graph theory can be found in Ref.［13］.

3 Main Results

In this section，firstly，synchronization problems are converted into asymptotic stability ones of multiple sub-systems with lower dimensions. Then， LMI conditions for synchronization are shown.Finally，an explicit expression of the synchronization function is presented.

Since the Laplacian matrix L of an connected undirected graph is symmetric，there exists U =with 1=［1， 1， …， 1］Tsuch that

where Λ=diag{λ2，λ3，…，λN}with 0=λ1＜λ2≤λ3≤ … ≤ λNdenoting the eigenvalues of the Laplacian matrix L.Let

where Id+ldenotes a d+l-dimensional unit matrix，then network(3)can be transformed into

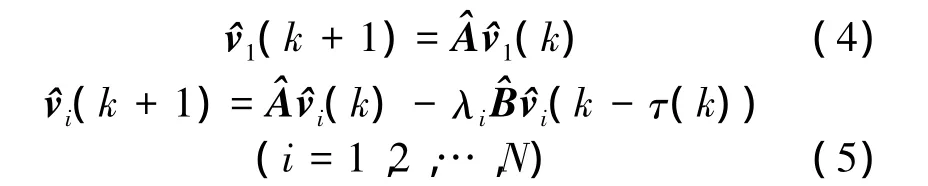
The following theorem gives a necessary and sufficient condition fornetwork (3)to achieve synchronization.

Theorem 1 Network (3) achieves synchronization if and only if subsystems(5)are asymptotically stable.

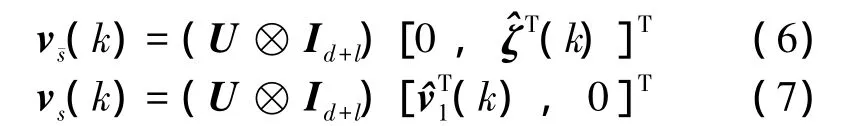
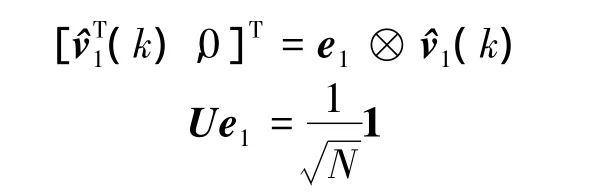
Due to where e1denotes an N-dimensional vector with 1 as its first entry and 0 elsewhere，it can be obtained by Eq.(7)that

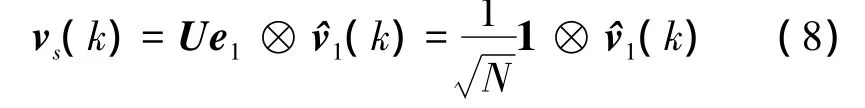
Since U⊗Id+lis nonsingular，from Eqs.(6)and (7)，vs(k)and v¯s(k)are linearly independent.Due to

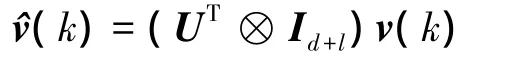
one can obtain by Eqs.(6)and(7)that

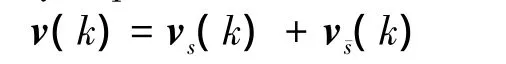
By the structure of vs(k)shown in Eq.(8)，network(3)achieves synchronization if and only if

When all states of each agent can be measured，synchronization protocols based on state errors can be used.However，in many practical applications，all states of each agent cannot be measured and only outputs，which are the linear combination of outputs or partial outputs，are available.In this case，two types of output feedback synchronization protocols;that is，static outputfeedback ones and dynamic output feedback ones can be used.It is well known that static output feedback synchronization protocols usually bring in more conservation.Hence，the current paper adopts dynamic output feedback synchronization protocols to reduce the conservation of LMI criteria in Theorem 1.

Theorem 1 transforms synchronization problems into asymptotic stability ones，but does not present direct criteria for synchronization.In the following，based on LMIs，synchronization criteria are proposed.

Theorem 2 For any τ(k)∈［1，¯τ］，network(3) achieves synchronization if there exist Ri= RTi＞0，Xiand Yisatisfying

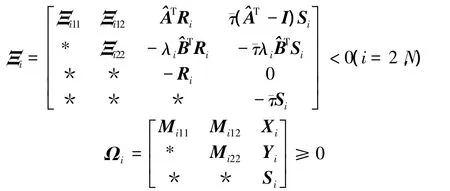
where

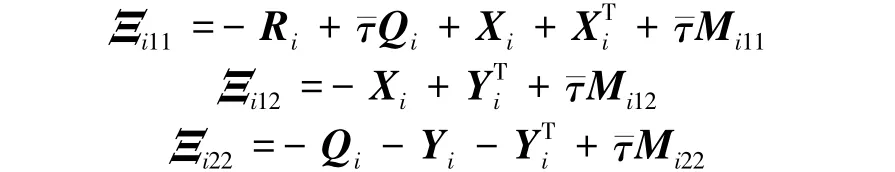
Proof Let

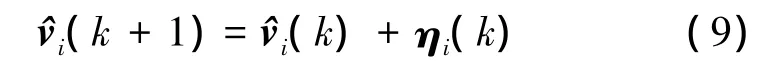
then one has

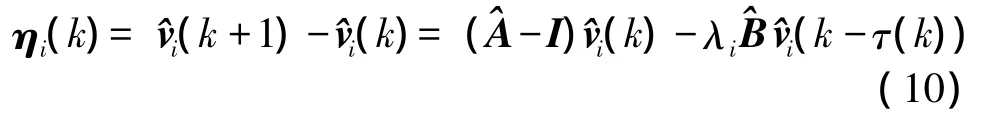
Consider the following Lyapunov function candidate

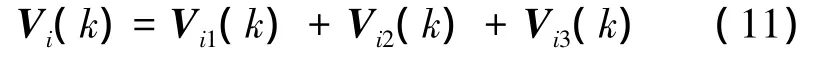
where

Define ΔVij=Vij(k+1)-Vij(k)(j=1，2，3)，and let

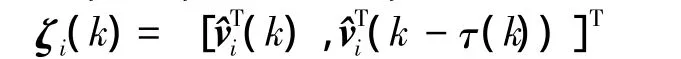
By Eq.(10)，the following equation can be obtained

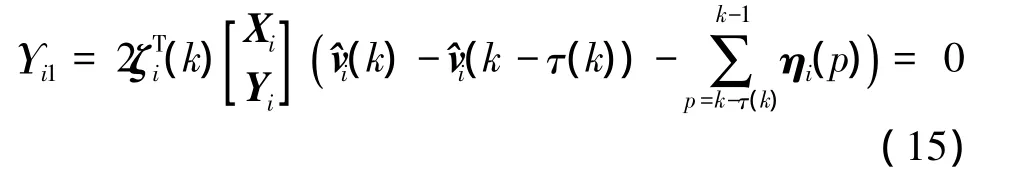
For

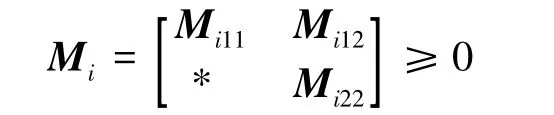
it can be shown that

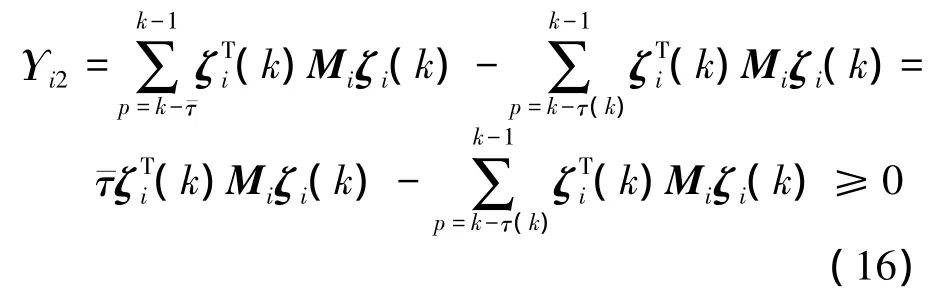
From Eqs.(11)to (16)， by Schur complement［14］，one can see that

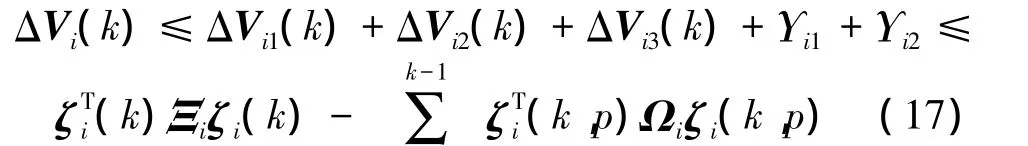
From Eq.(17)，one can see that if Ξi＜0 and Ωi≥0，then(i∈ {1，2，…，N})is asymptotically stable.Since LMIs have a convex property，from Theorem 1，the conclusion of Theorem 2 can be obtained.

When network(3)achieves synchronization，then states of all agents tend to be identical.The following theorem presents an approach to determine the identicalstate，thatis，the synchronization function.

Theorem 3 Ifnetwork (3)achieves synchronization，the synchronization function satisfies

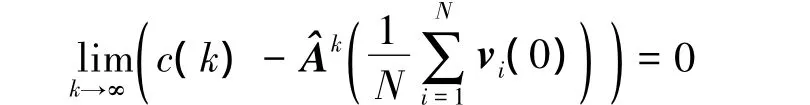
ProofSince^v(k)=(UT⊗Id+l)v(k)，one has

Due to

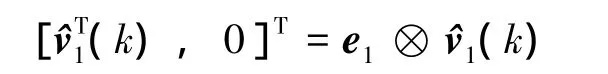
By Eqs.(7)and(18)，one has

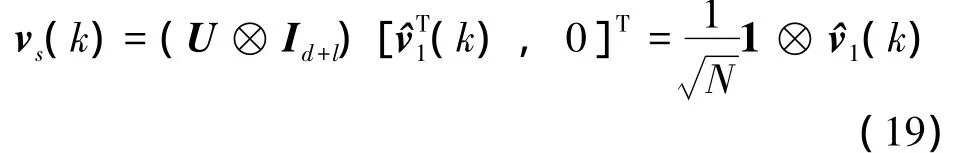
Due to

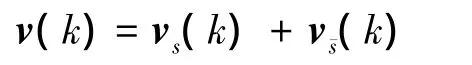
one has

By the proof of Theorem 1，if network(3) achieves synchronization，then

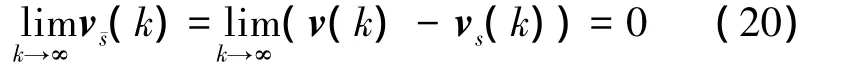
By Eqs.(19)and(20)，one can obtain that

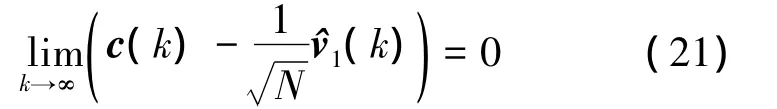
that is，subsystem(4)determines the synchronization function.By Eq.(4)，one has

By Eq.(18)，one can see that

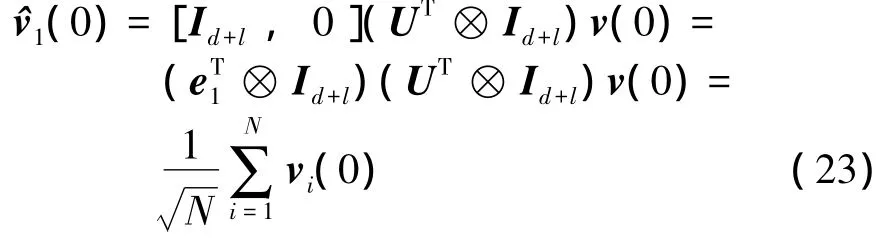
From Eqs.(21)to(23)，one can obtain that

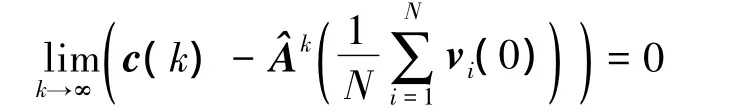
The proof of Theorem 3 is completed.

By Theorem 3，the synchronization function is independent of the time-varying delay and is dependent on the average value of initial states of all agents.It is notdifficultto find thataverage synchronization problems discussed in Refs.［5］and［15］are special cases of Theorem 3.

4 Numerical Simulations

It is assumed that a complex network consists of five homogenous agents with the dynamics of each agent described by Eq.(1)，where

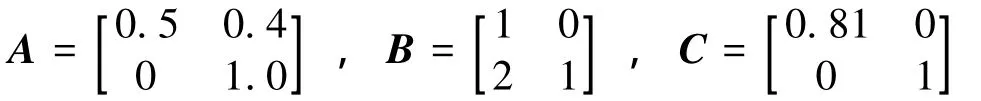
An undirected communication topology G of the complex network is depicted in Fig.1.Without loss of genrality，the adjacency matrix of G is set to be a 0－1.In this case，we can find that λ2=2 and λN=4.Let ¯τ=11.The initial condition is chosen as

Fig.1 Undirected communication topology

Let

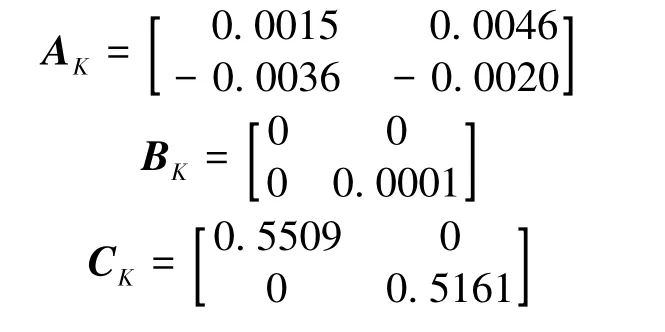
In this case，one can obtain that

By the FEASP solver in Matlab’s LMI toolbox［16］to check the LMIs in Theorem 2，one can find that Ξi＜0 and Ωi＞0(i=1，2)are feasible and

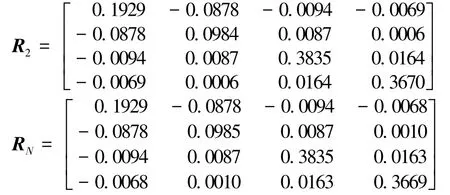
Fig.2 shows the state trajectories of the complex network，where the curves formed by circle markers denote the trajectories of the synchronization function given in Theorem 3.One can see that all state trajectories converge to the curves of the synchronization function;that is，the complex network achieves synchronization and the synchronization function can describe the synchronization state.Moreover，the single time-varying delay does not impact the synchronization function since the state trajectories do not deviate from the ones formed by circle markers.

Fig.2 State trajectories of the complex network

5 Conclusions

Synchronization analysis of high-order discretetime complex networks with time-varying delays is investigated by the dynamic output feedback synchronization protocol.A necessary and sufficient condition for complex networks to achieve synchronization is given and synchronization problems are transformed into asymptotic stability ones.Furthermore，LMI criterions for synchronization are presented.Moreover，an explicit expression of the synchronization function is given，which is dependent on the average value of initial states of all agents but is independent of the single time-varying delay.

［1］Klinshov V V，Nekorkin V I.Synchronization of time-delay coupled pulse oscillators.Chaos，Solitons＆ Fractals，2011，44(1):98－107.

［2］Lü J，Cheng G.A time-varying dynamical networks model and its controlled synchronization criteria. IEEE Transactions on Automatic Control，2005，50(6):841－846.

［3］ Lü J，Yu X，Chen G，et al.Characterizing the synchronizablity of small-world dynamical networks.IEEE Transactions on Circuits and Systems I:Regular Papers，2004，51(4):787－796.

［4］Chen Y，Lü J.Finite time synchronization of complex dynamical networks.JournalofSystemsScience and Mathematical Sciences，2009，29(10):1419－1430.

［5］Olfati-Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions of Automatic Control，2004，49(9): 1520－1533.

［6］Xiao F，Wang L.Consensus problems for high-dimensional multi-agent systems.IET Control Theory and Applications，2007，1(3):830－837.

［7］Wang J，Cheng D，Hu X.Consensus of multi-agent linear dynamic systems.Asian Journal of Control，2008，10(1): 144－155.

［8］Li Z，Duan Z，Chen G，et al.Consensus of multiagent systems and synchronization of complex networks:a unified viewpoint.IEEE Transactions on Circuits and Systems I: Regular Papers，2010，57(1):213－224.

［9］Xi J，Shi Z，Zhong Y.Output consensus analysis and design for high-order linear swarm systems:Partial stability method.Automatica，2012，48(9):2335－2343.

［10］XiJ， ShiZ， Zhong Y. Stable-protocoloutput consensualization for high-order swarm systems with switching topologies.International Journal of Robust and Nonlinear Control，2012.DOI:10.1002/rnc.2867.

［11］Xi J，Shi Z，Zhong Y.Output consensus for high-order linear time-invariant swarm systems.International Journal of Control，2012，85(4):350－360.

［12］Xi J，Shi Z，Zhong Y.Consensus analysis and design for high-order linear swarm systems with time-varying delays.Physica A，2011，390(23):4114－4123.

［13］Godsil C，Royal G.Algebraic Graph Theory.New York: Springer-Verlag，2001.

［14］Boyd S，Ghaoui L E，Feron E，et al.Linear Matrix Inequalities in System and Control Theory.Philadelphia，PA:SIAM，1994.

［15］Lin P，Jia Y.Average consensus in networks of multiagents with both switching topology and coupling timedelay.Physica A，2008，387(1):303－313.

［16］Gahinet P，Nemirovskii A，Laub A J，et al.LMI Control Toolbox User＇s Guide.Natick，MA:The Math Works，1995.