新型平尺直线度自动测量的方法
严雅君 陈 刚 / 上海市质量监督检验技术研究院
新型平尺直线度自动测量的方法
严雅君 陈 刚 / 上海市质量监督检验技术研究院
比较桥板法测量平尺直线度误差的方法和一种新型的自动测量方法,指出了桥板法测量的缺点,分析了自动测量的检测准确度高和实时采集数据计算的优势,并通过实例来比较两种测量方法的准确度,为平尺直线度误差测量提供了一种创新思路。
平尺;测量;桥板;直线度误差
0 引言
平尺是工作面为平面、用于测量工件表面直线度和平面度的量具。平尺准确度等级分为00级、0级、1级和2级。平尺一般由优质铸铁制造,也有选用花岗石或轴承钢制造。平尺作为确定直线基准的计量器具,其测量面的直线度误差是衡量平尺准确度的主要指标。平尺的直线度误差测量结果不仅关系到其自身的准确度等级,更会对被测工件的测量数据产生重大影响,因此如何确保平尺的直线度误差测量结果准确可靠成为一个重要的课题。
1 桥板法测量平尺直线度
根据JJF 1097-2003《平尺校准规范》的技术要求,对平尺直线度的测量采用桥板测量法,该方法测量桥板两个支撑点的相对倾斜角度,然后用各支撑点的测量数据进行评价得到其直线度。
测量方法是将被测平尺(桥型平尺除外)用等高块支承在距平尺两端2/9L(L为平尺长度)处,根据平尺长度选择适当桥板,一般不少于8~10个测量位置,跨距50 ~ 500 mm。把电子水平仪固定在桥板上,将桥板按照设定的跨距前后相接从平尺工作面的一端移动至另一端,每移动一个跨距就从电子水平仪上读取仪器数据。然后按照直线度评定方法进行数据处理得到平尺直线度测量结果,测量过程如图1所示。
桥板法测量由于桥板跨距可调,不受被测平板尺寸限制,因此在实际测量中应用较广。但是该测量方法也存在两个缺点。

图1 平尺直线度桥板法测量过程
(1)桥板移动方式为手工移动,无法真正沿直线移动及实现两次桥板位置的首尾相接,存在较大的测量误差。
(2)测量过程耗时较长,且无法实时计算测量结果,滞后时间长。
采取一种平尺工作面直线度自动测量的方法,就能得到更加准确的测量结果,确保平尺直线度测量数据的准确性,减小量值传递过程中产生的测量误差。特别是可对各种超长机床导轨及其他非标设备进行直线度测量,解决平尺及大尺寸机床导轨的直线度测量技术能力。
2 平尺直线度自动测量方法
采用自动测量装置对平尺工作面直线度进行测量,能改变传统的直线度手工测量的既定思路,消除测量过程中引入的定位误差,对各个测量位置实现准确定位及自动控制。
该方法采用光电自准直仪测量法取代电子水平仪进行测量。测量时自准直仪安装于三脚架上,三脚架固定支撑在地面,调整光电自准直仪的光束方向与平尺测量面平行,由于一般工厂车间通常具备地面防震结构,不会因震动对测量结果产生影响。用自动轻质小车取代桥板,小车底部用两个相同尺寸圆柱棒与平尺测量面相接触,保持小车与平尺测量面之间平移接触,两圆柱棒保持平行,两者间距离即为跨距。小车外侧有四个驱动轮与平尺侧向非工作面接触,安装步进电机驱动小车移动,驱动轮速度设计为50 mm/s,保持小车与平尺工作面的紧密接触及小车沿平尺移动的平稳性(如图2所示)。根据平尺工作面尺寸制作固定跨距为80 mm、100 mm、300 mm等多种规格的小车,在小车上安装无线发射模块、驱动电机和电路等,确保小车无线运行。

图2 小车与平尺接触方式
测量时,首先根据平尺尺寸选择合适的跨距小车,并在小车上固定反射镜;其次在计算软件中输入平尺参数,小车接收到计算机发出的测量指令后,按跨距尺寸平移;然后小车自动运行和定位,自准直仪发出的光束射向反射镜并返回镜头,在每个测量点小车自动停下,数据传输采用无线模块进行实时显示和采集,从而实现整个测量过程;最后将数据导入直线度测量软件进行评定,获得直线度误差结果后按校准规范中的准确度要求对平尺定级。整个测量过程不需进行任何人工操作,如图3所示。
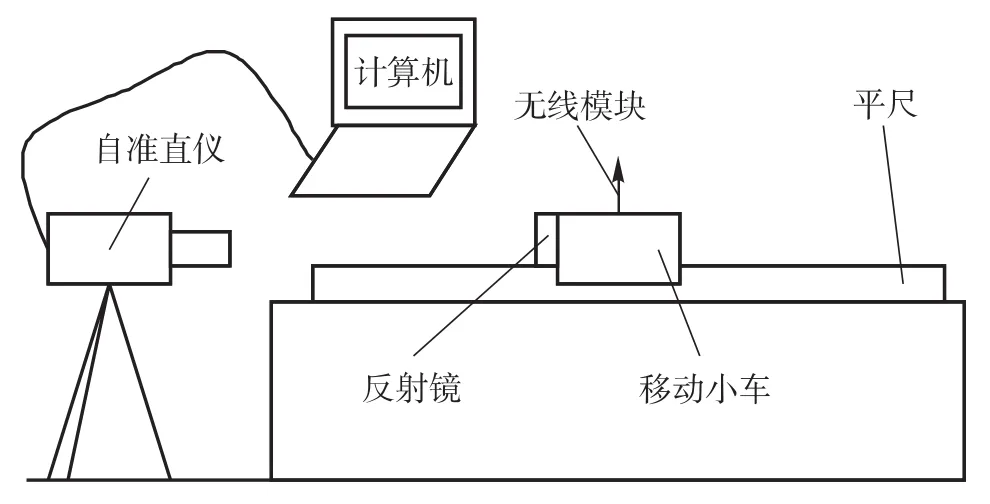
图3 平尺直线度自动测量系统
此法需用光电自准直仪,光电自准直仪代替电子水平仪测量直线度。光电自准直仪是依据光学自准直成像原理,通过LED发光元件和线阵CCD成像技术设计而成,由内置的高速数据处理系统对CCD信号进行实时采集处理,完成两个维度的角度测量。通过光学成像系统测量被测平面角度的变化,由光电转换系统敏感光学信号并将其转换为电信号供后续数据处理系统进行分析与评估。
光电自准直仪如图4所示,其测量直线度(倾斜角度)的基本原理如图5所示。光电自准直仪的测量范围约3 ~ 30 m,可以实现倾斜角度的准确测量,测量准确度可达±0.5″。

图4 光电自准直仪

图5 光电自准直仪测量原理
3 平尺直线度误差判定
用桥板法测量平尺直线度误差时,对直线度误差的评价方法主要有最小区域法、最小二乘法、两端点连线法。实际应用中,两端点连线法虽然计算简单但准确度较低,使用价值不大。最小二乘法的评定方法如果由人工计算较为复杂,数据处理较繁琐,不便于生产。最小区域法准确度最高,误差值最小且具有唯一性。因此通常情况下,采用最小区域法来计算直线度。
最小区域法是按最小包容区域的宽度评定直线度误差值,其判别的方法是:当两条平行直线包容误差曲线,若误差曲线上的高低点与上下包容线成相间的三点接触时,满足“低-高-低”或是“高-低-高”的相间准则(如图6所示),则此包容线构成的包容区域为最小区域。
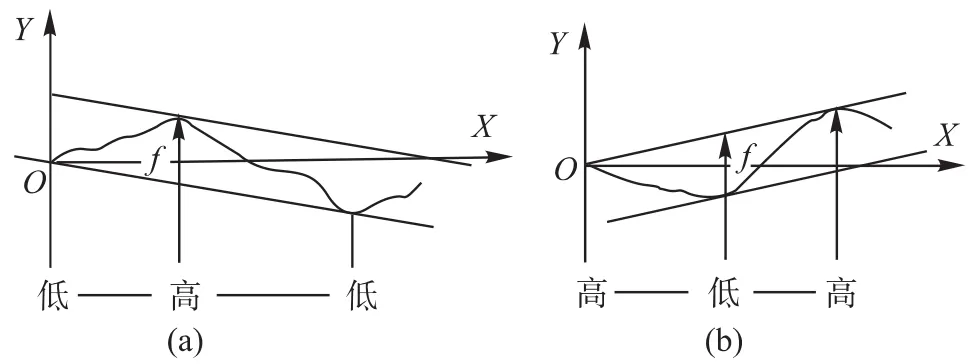
图6 包容区域
现以测量1 000 mm的铸铁平尺为例,分别通过桥板法和自动测量方法来校准平尺直线度。
3.1 桥板法测量直线度误差计算
使用JJF 1097-2003推荐的桥板法来测量平尺直线度。用分辨力为0.01 mm/m的电子水平仪校准,桥板跨距L=100 mm,电子水平仪在平尺工作面各点读数见表1。

表1 桥板法测量平尺直线度读数
用最小区域法计算平尺直线度误差,可以通过作图和计算公式来实现。图6中,x轴表示测量序号,y轴表示各测量位置相对起始点的读数累积值,将读数累积值在图中标出,连成一根误差曲线,依相间准则用两根平行直线包容误差曲线,形成图7中“低-高-低”的三点接触,构成最小包容区域。
图7中最高点和最低点已经明确,那么运用计算公式可以直接计算出符合最小区域法的直线度误差值。

图7 作图判断最小包容区域
设a、b、c分别为测量序号;而ya、yb、yc则分别为序号a、b、c的读数相对于测量基准的坐标值,且a、c为高(低)点,b为低(高)点,符合最小区域的直线度误差值f(单位:字)的计算公式为

依此计算,f= 11.5字。
当用电子水平仪测量平尺直线度时,平尺工作面直线度误差F(单位:μm)计算公式:

式中:C— 电子水平仪分辨力,mm/m;
L— 桥板跨距,mm;
f— 符合最小条件的平尺直线度,字
本例的平尺工作面直线度为
F=CLf= 0.01×100×11.5 = 11.5(μm)
从最小区域法作图计算平尺直线度误差的过程可见,需要花费较多的人工计算,且最小区域的判定较复杂,在实际生产、测量过程中还不是最方便。
3.2 自动法测量直线度误差计算
光电自准直仪所带的数据采集和分析系统,可以根据采集到的测量数据计算直线度,得出准确的直线度误差。过程由软件计算,提高了数据处理速度,实现了测量准确度更高的要求。具有数据实时采集、系统精确计算、结果可靠等优点,为生产者和检验者提供了便捷的方法。
测量上述的1 000 mm铸铁平尺,自动测量系统自动采集10个测量点的数据,计算出平尺直线度误差为10.6 μm。可见测量准确度比最小区域法作图计算得出的误差值小。根据JJF 1097-2003判断,定为1级。
4 结语
平尺作为直线度测量基准,对机械制造行业具有广泛的应用价值,因此必须确保其自身直线度测量结果的准确度。本文阐述的方法严格遵循了校准规范中的测量原理,并从根本上解决了平尺直线度测量过程中因手动测量引入的误差,利用自动测量的准确度高和数据实时采集的优势,大大提高了检测准确度和工作效率。此外还能推广应用到大尺寸平板平面度测量和角尺测量,具有较高的实用性和创新性,以及广泛的市场前景及可预见的经济效益。
[1] 全国几何量工程参量计量技术委员会. JJF1097-2003 [S]. 北京: 中国计量出版社,2003.
[2] 费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社,1987.
[3] 廖念钊,古莹菴,莫雨松,等. 互换性与技术测量[M]. 北京: 中国计量出版社,1991.
[4] 解广娟,刘正伟. 光自准直仪检测直线度误差[J]. 上海计量测试,2013,(4): 48-50.
[5] 焦燕萍. 一种测量长导轨直线度误差的新方法[J]. 上海计量测试,2014,(3): 56-57.
[6] 朱方源. EXECL环境下直线度最小条件计算[J]. 上海计量测试,2012,(3): 27-29.
[7] 赵东升,贾敏强,高冉,等. 最小二乘法直线度评定的不确定度分析[J]. 计量技术,2011,(5):66-68.
[8] 陈俊. 《平尺校准规范》存在的问题及建议[J]. 计量与测试技术,2013,(4): 77.
[9] 谭见闻. 基于MATLAB评定直线度误差[J]. 计量与测试技术,2011,(6): 18-19.
Method of automatic measurement for straightness error of the edges
Yan Yajun,Chen Gang
(Shanghai Institute of Quality Inspection and Technical Research)
Two methods of measuring the straight edges are compared. The disadvantage of the bridge frame method is indicated. Through example calculation to comparing two methods of measuring precision, detection precision and data-acquiring by computer are analyzed as the advantages of the new measuring method.
straight edges; measure; bridge frame; straightness error

