水平仪分度值误差校准结果不确定度评定

王汉斌

（福建省计量科学研究院，福建 福州 350003）

1 引言

框式、条式水平仪利用液面水平的原理，以水准泡直接显示角位移，测量相对水平和铅锤位置微小倾斜角度，也可用于测量各种机床导轨的直线度、平面度及平行度，校正设备安装的水平和铅直位置等[1]，广泛应用于汽车、机电、船舶、电梯等工业企业。

测量不确定度是与测量结果相关联的重要参数，表征合理地赋予被测量之值的分散性。合理评定测量不确定度，对保证校准结果的可靠性、进行被校准仪器的符合性判定具有重要意义[2-3]。

文中依据JJF 1084-2002《框式水平仪和条式水平仪校准规范》所述校准方法，分别通过GUM法和蒙特卡洛法（MCM），评定水平仪分度值误差校准结果的不确定度。

2 数学模型

依据JJF 1084-2002《框式水平仪和条式水平仪校准规范》，通过水平仪检定器构造标准角度，对水平仪分度值误差进行校准，如图1所示。

图1 水平仪分度值误差校准

水平仪的实测平均分度值可根据水平仪检定器的示值变化量与水平仪气泡的实测位移量计算，数学模型为：

水平仪分度值误差按式（2）计算：

实际校准中，常用相对误差表示被校水平仪的平均分度值误差，计算公式为：

实际应用中，水平仪检定器的常见分度值规格包括0.005mm/m、0.01mm/m[4]，被校水平仪的常见分度值规格包括：（0.02～0.10）mm/m[1]。文中以使用分度值为0.005mm/m的水平仪检定器对分度值为0.02mm/m的水平仪进行校准为例，说明不确定度评定方法，在该条件下，各参数取值如表1所示。

表1 参数取值

3 基于GUM法的不确定度评定

由式（3），分析不确定度来源，包括：水平仪检定器示值变化量引入的不确定度、水平仪气泡实测位移量引入的不确定度、水平仪检定器标称分度值误差引入的不确定度，分别计算各不确定度分量。

3.1 水平仪检定器示值变化量引入的不确定度

忽略起始点对线的影响，水平仪检定器示值变化量引入的不确定度主要源于人眼对于水平仪检定器示值的分辨力。设：

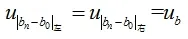
对于水平仪检定器示值，人眼的分辨力为0.1格，取均匀分布，则：

气泡在左、右两侧时，分别读数2次。故传递系数为：

水平仪检定器示值变化量引入的不确定度分量为：

3.2 气泡位移量引入的不确定度

忽略起始点对线的影响，气泡位移量源于人眼对气泡位移的估读，设：

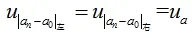
人眼的分辨力为0.1格，取均匀分布，则人眼对气泡位移读数分辨力引入的不确定度为：

进行读数重复性实验，数据如表2所示。

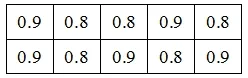
表2 重复性测量数据（单位：格）

根据规范[1]，实际测量中以2次读数的平均值作为测量结果，则重复性引入的不确定度为：

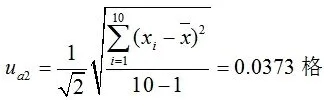
气泡在左、右两侧时，分别读数2次，故传递系数为：

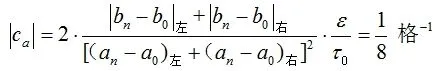
气泡位移量引入的不确定度分量为：

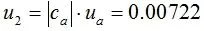
3.3 水平仪检定器分度值误差引入的不确定度

基于JJG 191-2002《水平仪检定器》，水平仪检定器分度值误差不大于标称分度值的6%，取均匀分布，其引入的不确定度为：

传递系数为：

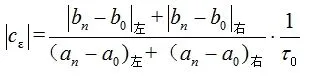
水平仪检定器分度值误差引入的不确定度分量为：

综合以上分析，不确定度分量如表3所示。

表3 不确定度分量一览表

计算合成标准不确定度为：

4 基于MCM的不确定度评定

基于式3，进行蒙特卡洛仿真，各参数分布类型如表4所示。

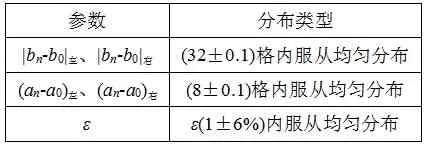
表4 各参数分布类型

仿真次数选择106次[5]。基于MATLAB进行仿真，仿真结果为：

95%包含区间为：[-5.9%，+5.9%]。

测量结果分布如图2所示。

图2 分度值误差测量结果分布

对比蒙特卡洛法和GUM法评定结果可知，两种方法评定结果基本一致，且扩展不确定度的量值与水平仪检定器的最大允许误差基本相当。水平仪检定器标称分度值误差，是水平仪分度值误差校准结果不确定度的主要来源。

5 结语

文中分别基于GUM法和蒙特卡洛法对水平仪分度值误差校准结果的不确定度进行评定，由评定结果可知，GUM法和蒙特卡洛法不确定度评定结果基本一致，水平仪分度值误差校准结果的不确定度主要源于水平仪检定器的标称分度值误差。蒙特卡洛法可回避灵敏系数计算等数学计算问题，其评定过程更为便捷。