人工势场和虚拟领航者结合的多智能体编队
曲成刚,曹喜滨,张泽旭
(1.哈尔滨工业大学卫星工程技术研究所,150080哈尔滨;2.哈尔滨工业大学深空探测基础研究中心,150080哈尔滨)
多智能体系统的研究是分布式智能控制研究的一个重要分支,它的目标是将大的复杂的系统(软硬件系统)分解成小的、彼此相互通讯及协调、易于管理的系统(即智能体),从而实现复杂系统的有机集成[1].多智能体的编队控制是指智能体之间形成或达到期望的距离和方位角.在陆地智能机器人编队、水下自主航行器编队、舰队的编队、无人机群编队、导弹集群编队控制,卫星星座的调度等方面,智能体之间的协同控制是一个不可回避的重要问题[2-6].
多智能体系统的编队控制形式主要包括队形形成、朝向目标、队形保持、队形变换和障碍规避等.目前主要的队形控制方法有:1)人工势场法,即通过定义人工势场得到相应的队形,但存在着队形单一,不同的队形需要定义不同的人工势场,势函数过于复杂等缺点[7-11];2)虚拟结构法,其缺点是应用范围很大程度上受到虚拟结构法形成的队形的限制[12];3)领航者-跟随者法,对领航者的依赖程度大,一旦领航者失效会导致整个队伍失效[13];4)基于行为的领航者-跟随者方法,该方法虽然通过增加候补领航者在一定程度上降低了对领航者的依赖程度,但也可能存在候补领航者在领航者之前失效的可能,此时,候补领航者就没有意义了[14].
本文将人工势场法和虚拟领航者法相结合,得到一种新颖的多智能体队形控制方法,不仅解决了对领航者的依赖问题,还能通过增加和布置虚拟体灵活地得到更多不同的队形.在编队控制过程中,智能体的运动规则是通过人工势场来确定的,智能体被完全驱动时,每个智能体的控制力可以看作是智能体所受合力减去智能体势能总和的梯度,这样的控制力使得智能体的总势能达到最小,利用局部势能可以使智能体群体形成一些规定间距的几何形状.此外,在控制过程中引入了虚拟领航者(不是指真实存在的),智能体和这些虚拟领航者之间的作用和真实智能体之间的作用是一样的,虚拟领航者的目的是指导群组或操纵这些群组的运动.
1 人工势函数
如图1所示,假设一群由n个智能体(黑色表示,图中为8个)和m个虚拟体(灰色表示,图中为3个)组成的多智能体系统.智能体的受力情况如图中箭头所示,这些力包含了智能体与任何一个相邻智能体的相互作用力.这个相互作用力是由人工势场产生的,其大小为fI,相应的势场函数为VI.

图1 队形控制示意
智能体的势场函数定义为
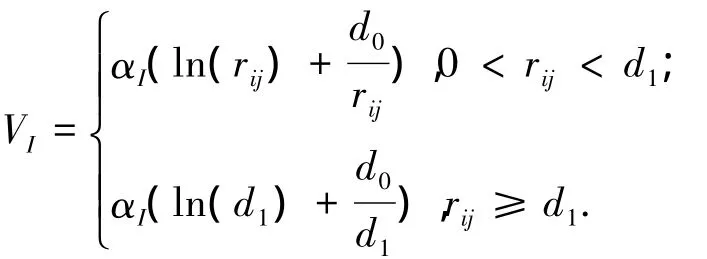
虚拟体的势场函数定义为
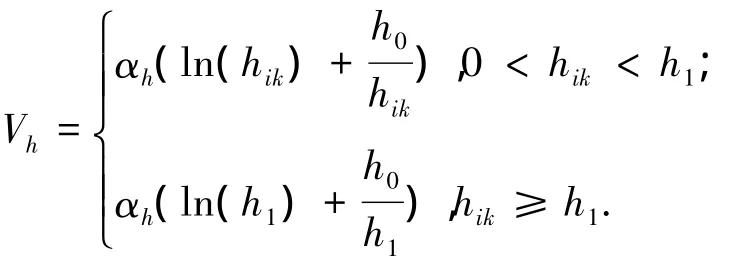
式中:rij、hik分别表示第i个智能体与第j个智能体和第i个智能体与第k个虚拟体之间的距离;αI、αh分别表示控制增益的标量;d1、h1分别表示智能体和虚拟体的势场影响范围;d0、h0分别表示智能体和虚拟体的最小势能点半径,当智能体与智能体之间的距离大于d0时,智能体之间表现为引力场,小于d0时,智能体之间表现斥力场,同理对于h0亦同,从而得到光滑的人工势函数.
对VI和Vh求偏导数可以表示智能体在相邻智能体和相邻虚拟体的人工势场中受到的势场力,它们的大小分别表示为
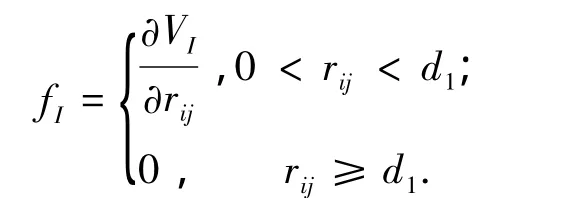
以及
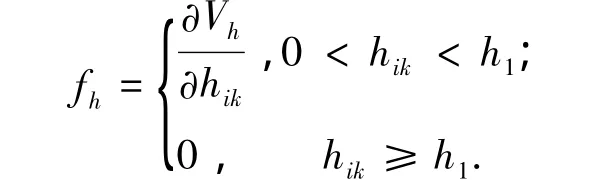
根据上述势函数定义及假设,可知势场力函数为连续函数.
除了上述两个力外,智能体还受到一个可控的耗散力fv,当智能体达到期望的速度时(也只有在智能体达到期望值时),fv为零.后文将用李亚普诺夫函数来证明其稳定性.
2 智能体的运动方程
在多智能体集群运动的队形控制中,考虑将参考点设在第0个虚拟体上,由于所有的智能体都跟随参考点运动,所以该虚拟体就相当于队伍的“虚拟领航者”.只要事先设定虚拟领航者的航向和速度,根据各智能体与其相对位置和相对速度就可以得到各智能体的位置和速度,进而得到整个智能体系统的航行状态,如图2所示.
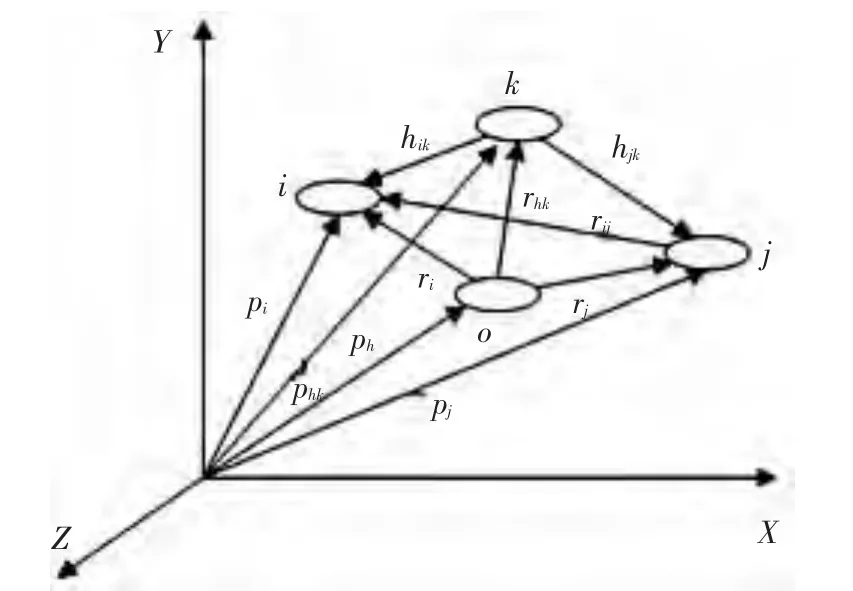
图2 智能体在惯性坐标系中的表示
假设pi为第i个智能体在惯性坐标系的位置,其中pi∈R3,i=1,2,…,n;第i个智能体的速度定义为vi=˙pi;假设智能体在完全驱动的情况下,得到智能体系统的运动方程为

假设第i个智能体的控制力为ui,其中i=1,2,…,n;这群智能体在虚拟领航者的引导下以v0(t)速度运动.以一个虚拟领航者为原点(如图中0号虚拟领航者表示)建立一个无旋转的惯性坐标系,第i个智能体相对原点的位置矢量用ri表示;相对地,其速度为˙ri=vi-v0.
智能体在运动坐标系中表示为
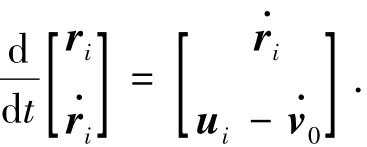
由于矢量rij=ri-rj,控制力ui可以表示为
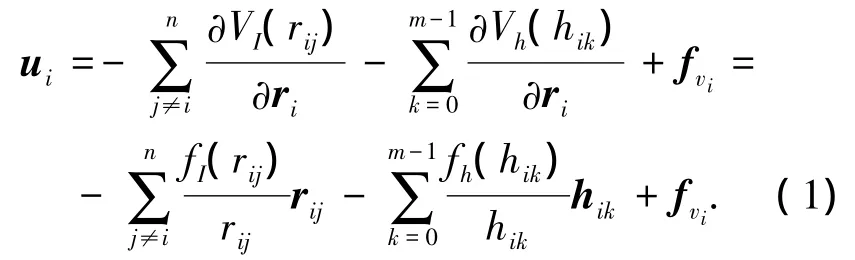
其中hi0≡ri,该控制律可以根据需要通过不同虚拟领航者的人工势场加以修改.
3 系统稳定性分析
如果没有能量耗损,根据李雅普诺夫稳定性判据,多智能体系统是局部渐近稳定的,当存在不确定性时,相应的稳定平衡也存在对称性.在一般情况下,考虑定义在状态空间的李雅普诺夫函数一般形式为
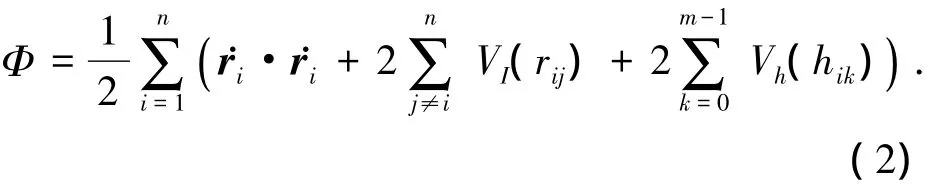
上式对时间求导得

求导过程中使用了式(1)中控制律ui,因此,如果选择fvi=-ai˙r,ai>0,(i=1,2,…,n),则 ˙Φ是负定的,而有且只有当对所有的i都有˙ri=0的时候,˙Φ等于0.
系统期望达到的运动状态是各智能体与虚拟领航者之间的相对速度为零,即;从而使得每个智能体与领航者之间的相对位置为常值,即保持一定的编队构型.由于Φ≥0,则当 Φ˙ <0时,即在足够长的时间内,Φ(t)=0;又因为式(2)中构成Φ的三项均大于等于零,因此当Φ(t)=0时,必有
利用LaSalle不变性原理可以得到:已经临近稳定并且无耗散的平衡状态将以这种无耗散形式达到渐进稳定.
考虑一组通过定义的动态智能体系统,V0是常数,控制律由式(1)给出(其中控制律是光滑的),˙ri=0这种平衡可表示为下面的形式:
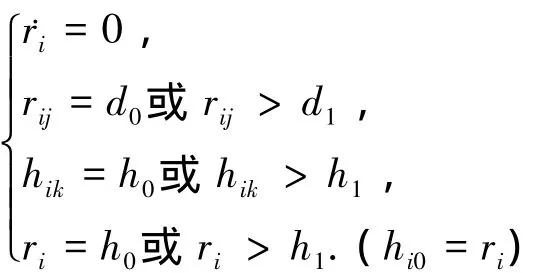
上式对所有的i,j=1,2,…n,j≠i和k=1,2,…,m-1都成立.假设h1和d1都已经被定义,将会在一定区域内达到全局渐进稳定,平衡点是全局人工势能之和最小处.在没有对称性的情况下,稳定的全状态空间可以得到实现;在有对称的情况下,所有智能体的相对速度也将归零,每个对称变量将变成稳定的常数.
4 仿真实验与分析
在集群运动的情况下,根据智能体个数的不同,智能体的位置呈现不尽相同的不确定性,即智能体的位置不唯一.为了打破这种不确定性,可以通过在原有的虚拟领航者的对称位置或没有智能体的位置上增加新的虚拟领航者来实现.
1)队形形成.考虑由4个智能体(深灰色)和2个虚拟领航者构成的二维编队队形拓扑图如图3所示,其中4个智能体在2个虚拟体的作用范围内.
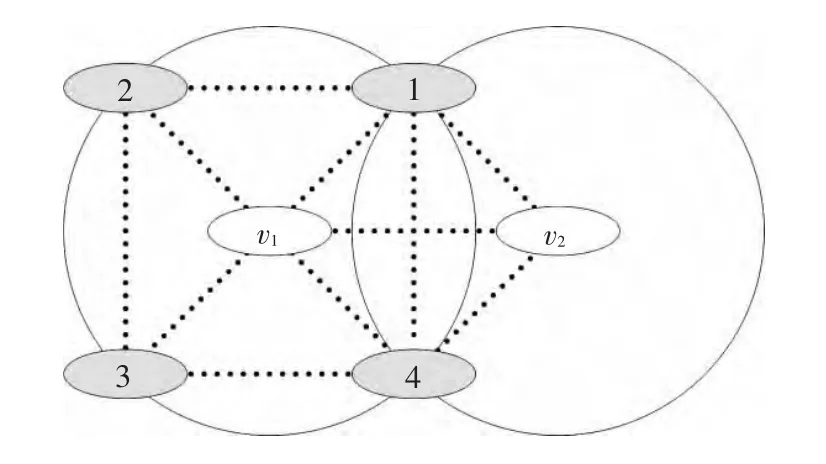
图3 多智能体系统编队信息交换拓扑图
假设虚拟领航者的运动方程为
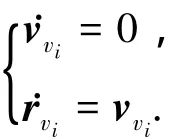
其中i=1,2.智能体之间的期望距离为2;在笛卡尔坐标系下,1号虚拟领航者和2号虚拟领航者的速度都为[2,0],初始位置分别为[4,0],[2,0]; 4个 智能体的初始位置为[0,- 1.5],[0,-0.8],[0,1.5],[0,1.4],初始速度均为[0,0].为了更好地观察队形的变化,在笛卡尔坐标系下显示仿真结果.根据虚拟领航者的动力学模型,虚拟领航者将进行匀速直线运动,仿真结果如图4~5所示,其中图4(a)为4个智能体和2个虚拟领航者构成的系统在队形形成过程中,智能体运动平面内的运动轨线图,图4(b)为最终形成的队形图,图5中(a)和(b)分别为智能体系统分别沿X轴和Y轴的速度变化曲线.
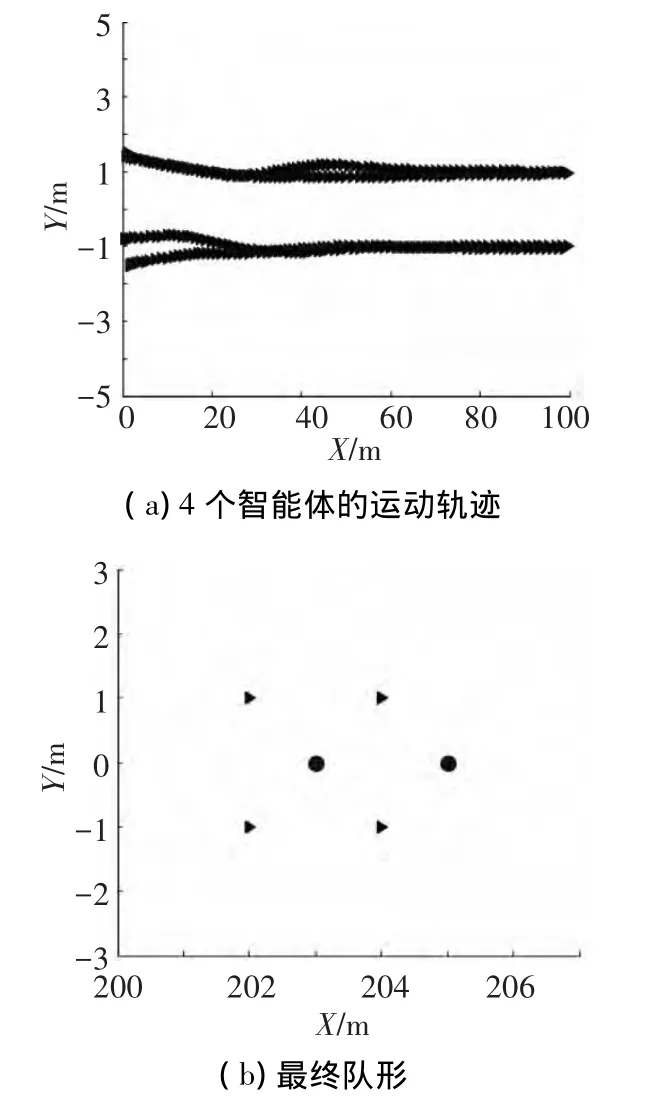
图4 4个智能体和两个虚拟领航者的编队
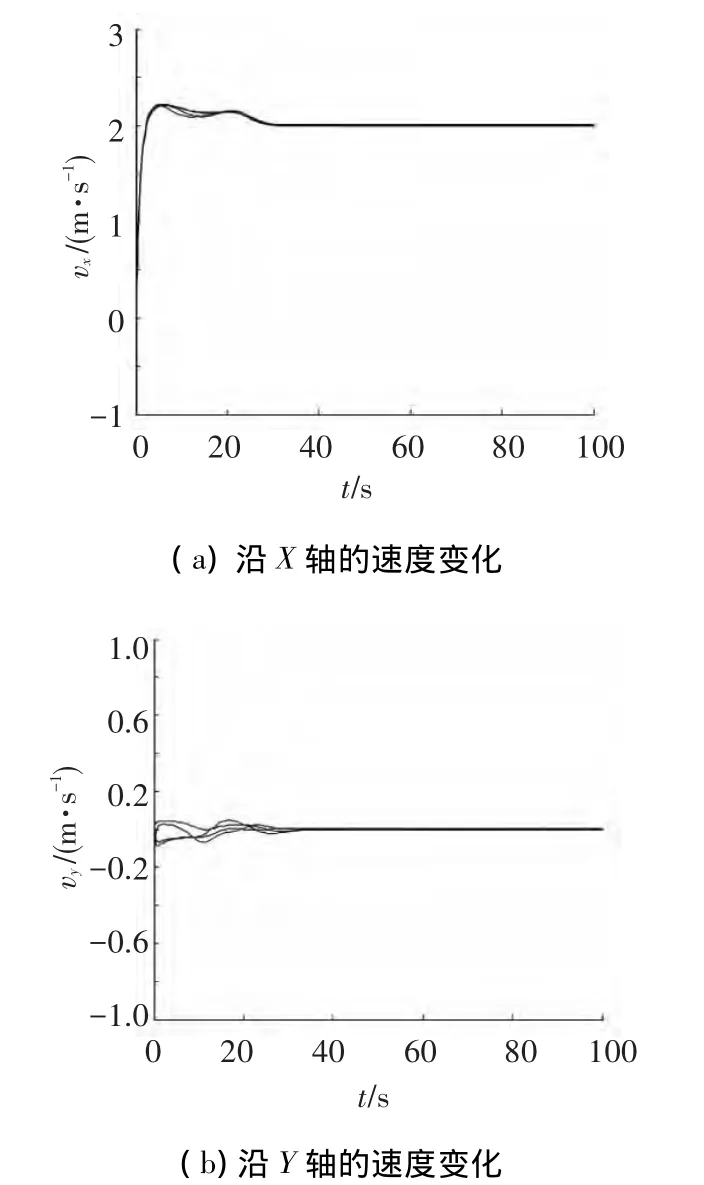
图5 4个智能体的速度变化曲线
由仿真结果可以看出,由4个智能体和2个虚拟领航者在人工势场下系统的运动速度和智能体之间的距离都能够达到期望值.
2)队形变换.考虑将上面仿真得到的正方形队形变换到直线形队形,4个智能体与5个虚拟领航者之间、智能体之间的信息交换拓扑图,以及各智能体在虚拟领航者作用范围内的期望位置如图6所示.
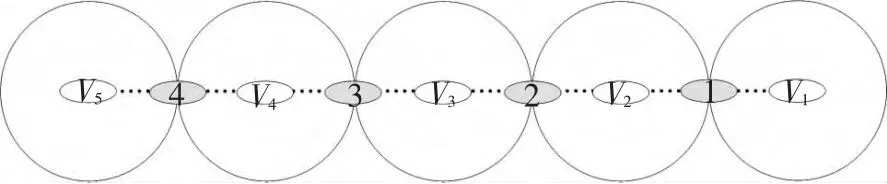
图6 多智能体系统队形变换信息交互拓扑
同样假设智能体之间的期望距离为2,5个虚拟领航者的速度都为[2,0],它们之间的距离也为2,虚拟领航者将进行匀速直线运动.仿真结果如图7~8所示.图7(a)和(b)为智能体系统分别沿X轴和Y轴的速度变化曲线,图8中(a)至(f)描述了队形的变换过程.
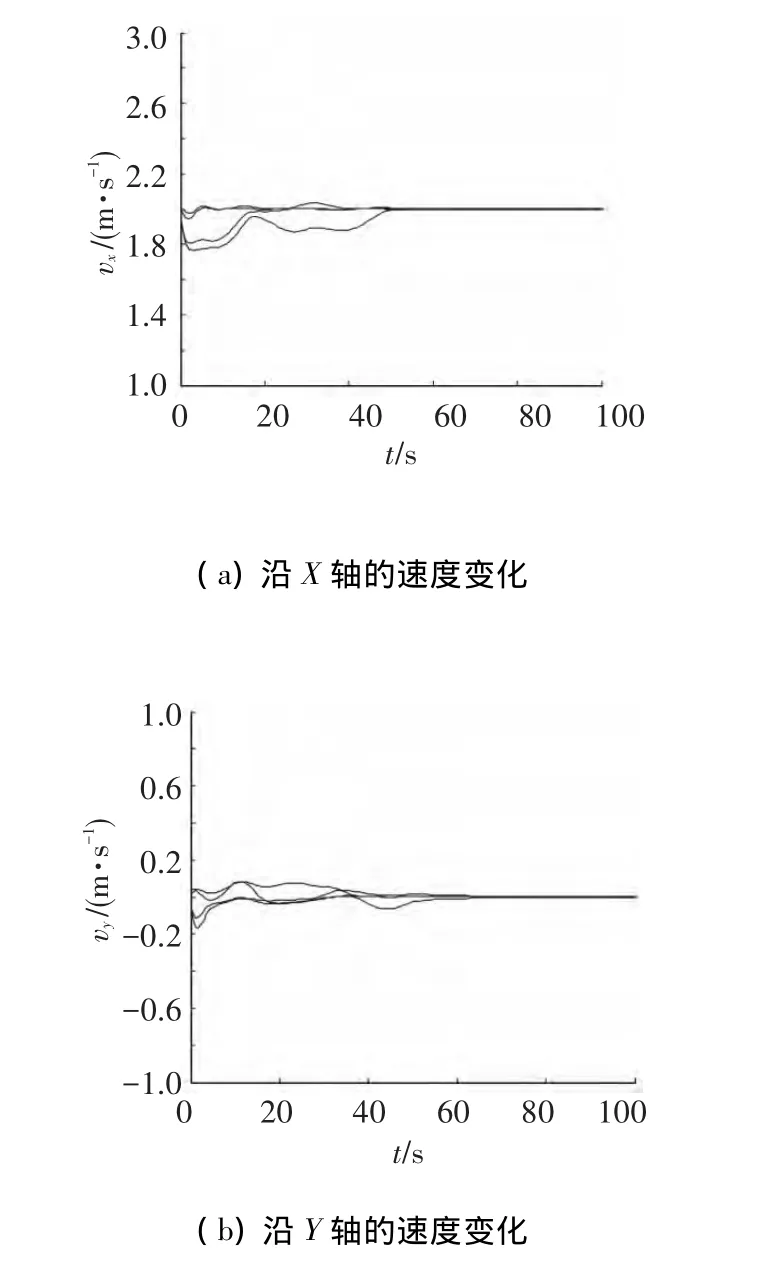
图7 4个智能体的速度变化曲线
从仿真结果可以看出,4个智能体在5个虚拟领航者的作用下形成了直线队形,速度和位置都达到了期望值.
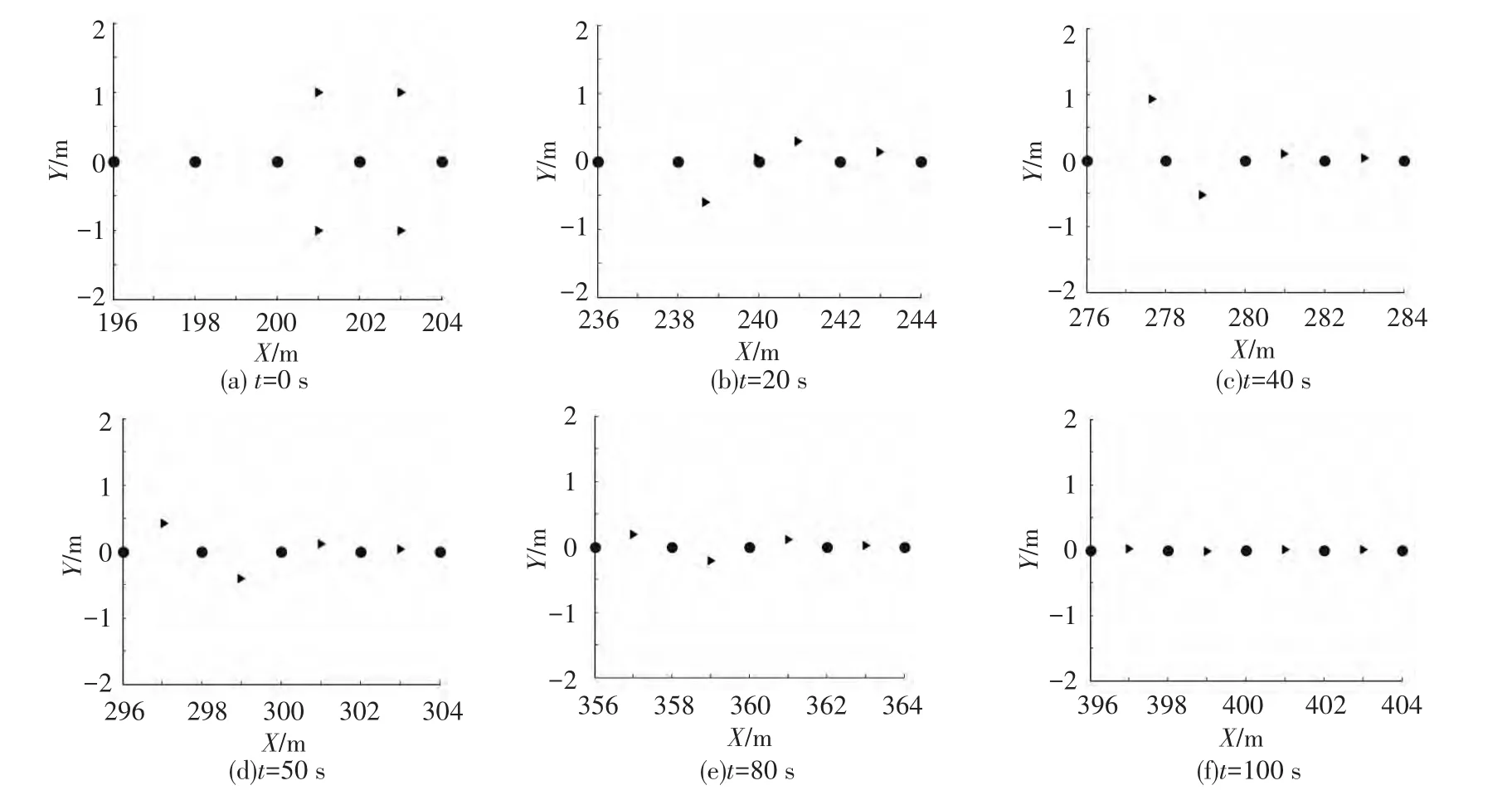
图8 多智能体系统队形变换过程
5 结语
对多智能体的研究主要针对智能体个体之间的相互通信、协同合作及冲突消解,本文针对协同合作提出了一种基于人工势场结合虚拟领航者的多智能体系统协同控制方法.这种方法首先建立智能体与虚拟领航者之间的人工势场函数,其次通过对智能体的运动学方程的分析,给出智能体的控制力,进而完成队形保持与变换,并利用多智能体系统的动能和势能的总和作为李亚普诺夫函数,验证了多智能体的集群运动和系统的稳定性.仿真实验表明,该方法能够实现队形的保持与变换,具有一定的应用前景.
[1]刘金琨,王树青.复杂系统多智能体不一致性问题的研究[J].控制与决策,1999,14(3):249-252.
[2]BELTA C,KUMAR V.Abstraction and control for groups of robots[J].IEEE Transactions on Robotics,2004,20 (5):865-875.
[3]王晓燕,王新民,肖亚辉,等.无人机三维编队飞行的鲁棒H∞控制器设计[J].控制与决策,2012(12): 1907-1911,1916.
[4]王银涛,严卫生.多自主水下航行器系统一致性编队跟踪控制[J].控制理论与应用,2013,30(3):379-384.
[5]马培蓓,纪军.多导弹三维编队控制[J].航空学报,2010,31(8):1660-1666.
[6] SU Housheng.Flocking in multi-agent systems with multiple virtual leaders based only on position mesurements[J].Communications in Theoretical Physics,2012,57(5): 801-807.
[7]KOKSAL M I,GAZI V,FIDAN B,et al.Tracking a maneuvering target with a swarm of non-holonomic agents using artificial potentials and sliding mode control[C]//In Proceedings ofthe 16th Mediterranean Conference on Control and Automation.Piscataway: IEEE,2008:1174-1179.
[8]周稼康,胡庆雷,马广富,等.基于一致性算法的卫星编队姿轨耦合的协同控制[J].系统工程与电子技术,2011,33(4):825-832.
[9]MOHAMED E F,EL-METWALLY K,HANAFY A R. An improved TangentBugmethod integrated with artificial potential field for multi-robot path planning[C]//2011 International Symposium on Innovations in IntelligentSystems and Applications (INISTA). Piscataway:IEEE,2011:555-559.
[10]LIANG Y,LEE H H.Decentralized formation control and obstacle avoidance for multiple robots with nonholonomic constraints[C]//Proceedings of the 2006 American Control Conference.Minneapolis,Minnesota:[s.n.],2006:5596-5601.
[11]LEONARD N E,FIORELLI E.Virtual leader,artificial potentials and coordinated control of groups[C]// Proceedings of the IEEE Conference on Decision and Control.Piscataway:IEEE,2001:2968-2973.
[12]REN W,BEARD R W.A decentralized scheme for spacecraft formation flying via virtual structure approach[C]//Proceedings of the American Control Conference. Piscataway:IEEE,2003:1746-1751.
[13]CHEN X P,SERRANI A,OZBAY H.Control of leader follower formations of terrestrial UAVs[C]// Proceedings of the IEEE Conference o n Decision and Control.Piscataway:IEEE,2003:498-503.
[14]BALCH T,ARKIN R C.Behavior-based formation control formultirobotteams[J].IEEE Transactions on Robotics and Automation,1998,14(6):926-939.

