自适应选取聚类中心K-means航迹起始算法

宫峰勋，戴丽华，马艳秋

(中国民航大学电子信息工程学院，300300天津)

航迹起始是航迹处理中的首要问题.航迹起始算法有两大类.强杂波环境下的航迹起始是研究的重点，研究数据表明批处理技术用于起始强杂波环境下目标的航迹具有很好的效果，主要包括Hough变换法等［1-6］.

在多部传感器同时监视某一空域的多批目标时，在某一时刻，融合中心接收到多部传感器的量测数据呈团状，且大致分布在目标真实值的周围［5］.如何从这些量测数据中区分出源于不同目标的数据，这是实现目标跟踪的重要问题.文献［5］应用模式识别理论中的聚类思，进行量测数据的聚类，实现不同目标量测数据的归并，但未给出聚类中心和聚类半径的求解明确说明.当前聚类方法中K-means算法是最为广泛应用的基于划分的聚类方法，标准的K-means聚类估计存在诸如事先给定聚类数目k、聚类结果依赖初始聚类中心的选择等等.标准K-means聚类算法的改进也就应运而生［7-10］.这些改进方法虽然克服了标准K-means算法随机选取初始聚类中心的缺点，能够一定程度上加快算法的收敛速度，提高算法的效率，但大多需要预先给定聚类数目，并没有解决因预设聚类数目不准确给聚类结果带来的影响.因应多传感器观测值的分布态势，本文推出一种新的K-means聚类方法，其基本思想是自适应修正选取初始聚类中心，即对每一时刻的多部传感器的量测数据进行修正性聚类，通过递进式选择度量两个量测数据不相似性的阈值，自适应的选取聚类数目和初始聚类中心，使每个聚类中的数据代表同一个目标，递进获得各聚类中心，从而将多传感器的航迹起始问题简化为单传感器的航迹起始问题，不仅解决标准K-means算法的两大缺点，同时也提高了算法的效率;然后对该聚类量测数据采用修正的逻辑航迹起始算法进行目标航迹起始估计.实验仿真结果表明，这种递进式自适应算法是可行的、结果正确.

1 自适应测量数据聚类算法原理

多传感器量测数据的分布特征要求在聚类算法的选择时必须满足:

1)目标类别数未知;

2)有较强的鲁棒性，个别虚警和漏警的存在不会影响分类结果.

基于以上两个方面的考虑，本文采用改进的K-means聚类算法.

1.1 标准的K-means聚类算法

K-means聚类算法的基本思想:随机选取k个初始聚类中心，其中k为聚类个数，然后计算各数据对象到初始聚类中心的欧氏距离，并把它们指派到离它们最近的那个聚类中心所在类;对调整后的新类，更新聚类中心;重复指派和更新过程，直到聚类中心不再发生变化为止［11］.

分析可知，K-means聚类算法必须给定聚类数目k，很多时候事先并不知道给定的数据集应该分成多少个类别才合适;且K-means聚类结果依赖于初始聚类中心的选择，选择不同聚类结果相异.由于随机选取K-means的初始聚类中心，结果导致聚类结果不确定，还会出现有些类中可能没有选中的数据对象，而有些类中可能选中多个数据对象，若以这样的初始聚类中心来对数据对象进行聚类，其聚类结果肯定是不正确的.

1.2 自适应初始聚类中心选取的K-means聚类算法

通常量测数据呈团状分布，且分布在以真实值为中心范围，由于未知目标个数，故不宜直接采用标准K-means时需要注意应用条件.针对要求预先给定聚类数目的问题，这里研究并给出一种修正的自适应初始聚类中心的选取方法.衡量数据对象间的相似性可采用距离来实现聚类估计.若能估计出度量任意量测数据间相似性的阈值，则可确定聚类的数目以及初始聚类中心［14-15］.

假设传感器数目为Ns，样本数据集为X=表示聚类的k个类别，聚类中心为cj(j=1，2，…，k)，度量两个量测数据不相似性的阈值为ε，改进的K-means聚类算法选取初始聚类中心的准则为:若d(xi，cj)＞ε，则 xi不属于 Cj类， 其中 d(xi，cj)=

算法步骤:

2)估计数据集内随机观测值xi，xj间的空间距离D(xi，xj)并按升序排列，放进数集D;

3)随机选取一观测值为初始聚类中心，且取聚类数目k=1，两观测值相似性的阈值取为

4)估计集合内其余观测值与给定初始聚类中心间的空间距离，选中极小值与比较.如果大于，则聚类数量进1，于是获得更新的聚类中心;如果小于，否则将此点与选取的聚类中心归为一类.同时相似性阈值的数值被更新为

5)重复步骤4，直至数据集中所有数据都已分类完毕.

6)输出初始聚类中心.

得到初始聚类中心以后就可以按照标准K-means聚类算法的一般步骤对量测数据的聚类进行调整，直到聚类中心不再发生变化为止，输出的聚类中心就是各个目标的航迹.

假设聚类前测量数据已经过时空校准，各观测单元的工作时间一致.算法结束后得到的k即为目标个数，输出的聚类中心作为K-means聚类算法的初始聚类中心.

如上所述，着眼于初始聚类中心分类的正确性是由观测值间不相似性的阈值决定的.合适选取的阈值，较为准确的聚类和初始聚类中心获得奠定基础.由于一种聚类集合中不会出现两个量测点迹来自相同传感器，故一个聚类含有的观测值数量应不多于所有观测扫描到的航迹数.考虑到同一时刻对单个目标的多传感器观测值聚集为团状及各传感器同一时刻对同一目标的观测值呈状态分布的特点，估算各聚类中观测数据的最大距离并逐个比较，获得的最大值作为度量观测值间不相似性的阈值.若集中任意一点的测量值与初始聚类中心的最小空间距离大于预定阈值，则此观测值属于新目标;若小于阈值，则认为此量测数据与其最近的初始聚类中心源于同一目标，即属于同一聚类［16-18］.

图1所示为度量两观测值间不相似性阈值的方法，其中a～c区代表获得的聚类，d1，d2，d3分别为聚类a～c区中相距最远的两点间的空间距离.如图1可见，聚类a中两点间的距离最大，则度量两量测数据不相似性的阈值取d1.

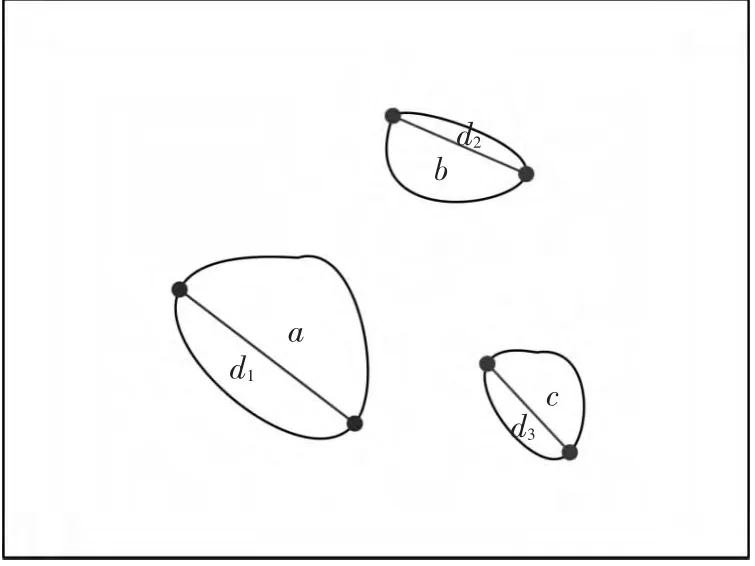
图1 不相似性阈值选取示意

实验仿真结果表明:采用改进的K-means聚类算法推得的自适应初始聚类中心方法获得的聚类优于随机选择的估算方法.假设有3部传感器对10个目标进行跟踪.图2(a)为标准K-means算法采用随机方法选取初始聚类中心的聚类结果，圆圈表示更新后的聚类中心，相同形状的点表示同一聚类.图2(b)所示为采用本文方法提取初始聚类中心的估计结果.由图2(a)和(b)所示估计结果可知，随机选取聚类中心方法性能较差，有些观测值集合中出现2个聚类中心，有些目标观测值集中却没有选中的聚类中心，因而就出现观测值集分批和合批的现象;考虑到多部传感器观测值在空间呈团状分布的特点，这里的估计方法中采用相似性空间距离度量方法，选择最小空间距离为阈值，可达到良好的聚类估计结果.

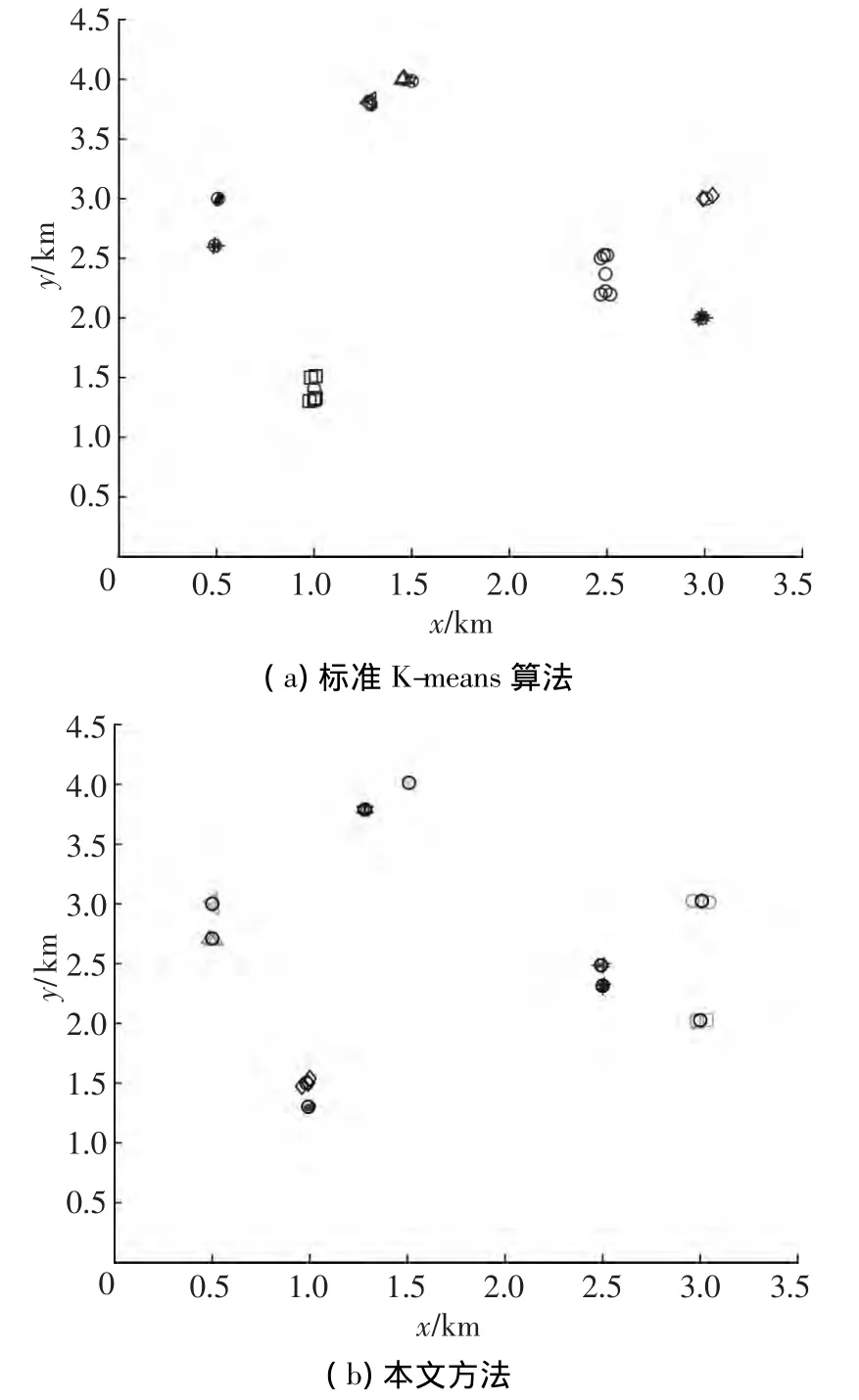
图2 不同初始聚类中心选取方法的聚类结果

2 航迹起始算法分析

经过改进的K-means聚类过程，整个多传感器系统就可以简化为单传感器估计的情况，航迹起始过程也大大简化.这里采用修正的逻辑航迹起始算法对多传感器观测值进行起始航迹估计，并根据空间阈值对估计算法进行修正.

2.1 修正的逻辑航迹起始算法

在实际应用中采用文献［7］的研究结果，给出落入波门观测值与可能航迹一致的限制条件，达到剔除与可能航迹成V字形的航迹结果.对于落入波门内的量测，假设与该可能航迹的第2个点的连线与该航迹的夹角为α，若α≤θ(θ一般由测量误差决定，为保证很高的航迹起始概率，θ可以选择较大)，则认为与该航迹关联［2］.

2.2 角度限制条件的选取

目标观测点迹的连线与该航迹夹角的限制条件α≤θ中θ的选择，影响修正的逻辑航迹起始算法的准确性与可靠性.只有选择合理的θ才能达到更好的性能.文献［7］虽然详细阐述了修正的逻辑航迹起始方法的步骤，但是对角度限制条件如何选择却并没有做出说明.本文通过实验仿真，给出了合理选择θ的方法.

仿真环境中有10个目标，且它们保持匀速直线运动状态，其中使用3部二维传感器对这些目标进行跟踪，目标初始位置分别为(2.5，2.3)、(2.5，2.5)、(3.0，3.0)、(3.0，2.0)、(1.0，1.5)、(1.5，4.0)、(1.3，3.8)、(1.0，1.3)、(0.5，2.7)、(0.5，3.0)，单位为km.这些目标的速度均为v= 200 m/s.令该传感器采样周期T=1 s，测向误差和测距误差分别为σθ=0.3°和σr=20 m，威力范围A0=2×108m2，波门半径r=300 m.估算的航迹检测概率与虚假航迹起始概率随θ变化曲线如图3所示.令测距误差取值为(20 m，30 m，…，60 m)，θ的取值为(0，π/18，2×π/18，…，π)，做1 000次蒙特卡洛实验，统计得到的航迹检测概率曲线如图3所示.由图3所示的航迹检测概率与θ间的变化曲线分析得，首先其随着θ的增大先上升，进而保持不变，然后再下降，航迹检测概率曲线是以θ=π/2为对称中心.

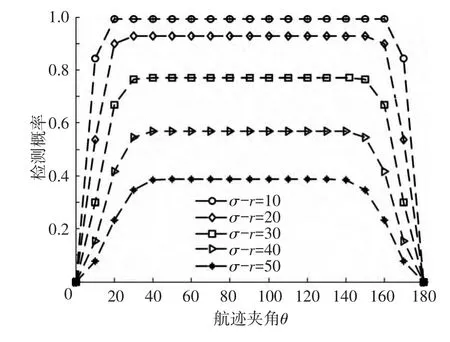
图3 航迹检测概率θ的变化曲线

令θ取值为(0，π/18，2×π/18，…，π)，单扫周期的杂波数λ取值为(50，100，…，250)，做1 000次蒙特卡洛仿真，计算得到的假航迹起始概率曲线如图4所示.假航迹起始概率随着θ的增大呈上升趋势.

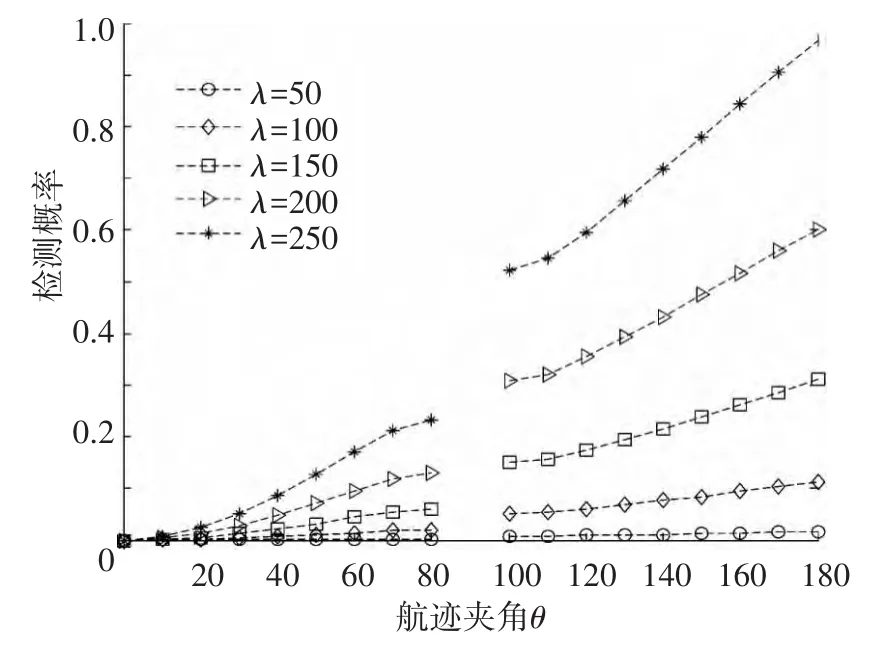
图4 假航迹检测概率随θ的变化曲线

本文仿真实验假定传感器测距误差为σr= 20 m，一个扫描周期内的杂波数λ=50，如图3所示可知，航迹检测概率在航迹夹角θ=20°时达到最大值，而假航迹起始概率在0≤θ≤π/2时随着θ的增大呈上升的趋势.基于航迹检测概率和假航迹起始概率参数的考虑，蒙特卡洛仿真中采用的可能航迹点连线与航迹夹角θ应取20°.

综上分析可知，θ的选择跟传感器的测距误差有关.若使修正的逻辑航迹起始算法的性能达到最佳，需要在确定的测距误差和杂波数的条件下，选取最大航迹检测概率值的同时使假航迹起始概率最小的θ.

3 聚类与航迹起始仿真

仿真环境中有10个目标，且它们保持匀速直线运动状态，其中使用3部二维传感器对这些目标进行跟踪，目标初始位置分别为(2.5，2.3)、(2.5，2.5)、(3.0，3.0)、(3.0，2.0)、(1.0，1.5)、(1.5，4.0)、(1.3，3.8)、(1.0，1.3)、(0.5，2.7)、(0.5，3.0)，单位为km.这些目标运动速度为v= 200 m/s.同时假定雷达的采样周期T=1 s，雷达的测向误差和测距误差分别为σθ=0.3°和σr=20 m.

3.1 量测数据聚类仿真分析

图5所示为目标的真实航迹分布，不同形状的点代表不同的目标.图6所示为各传感器的量测数据分布.图7所示为采用标准K-means聚类算法对传感器量测数据进行分类的结果.图8所示是采用本文改进的K-means聚类算法对传感器量测数据进行聚类的结果，相同形状的点表示源于同一目标，总共识别出10个目标.比较图7、8所示仿真结果可知，本文提出的改进的K-means聚类算法可实现对量测数据正确聚类，能正确识别出目标的个数，而标准K-means聚类算法并不能对量测数据进行正确的分类，即无法识别出目标.图9所示为采用改进的K-means聚类算法得到的聚类中心，即分辨出的目标航迹.

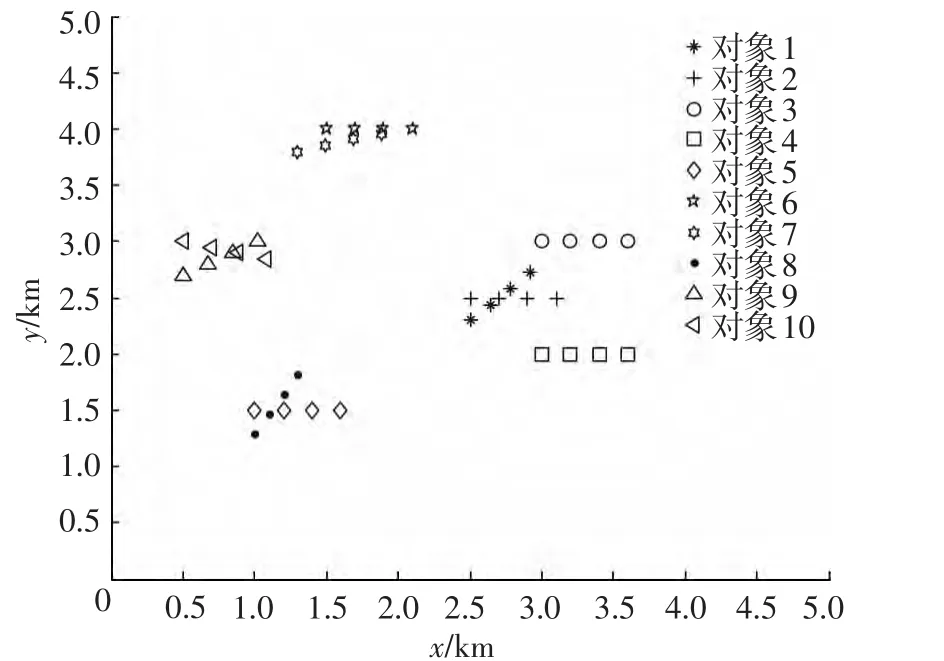
图5 目标真实航迹

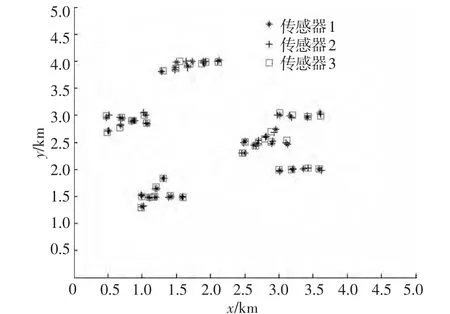
图6 传感器量测数据分析

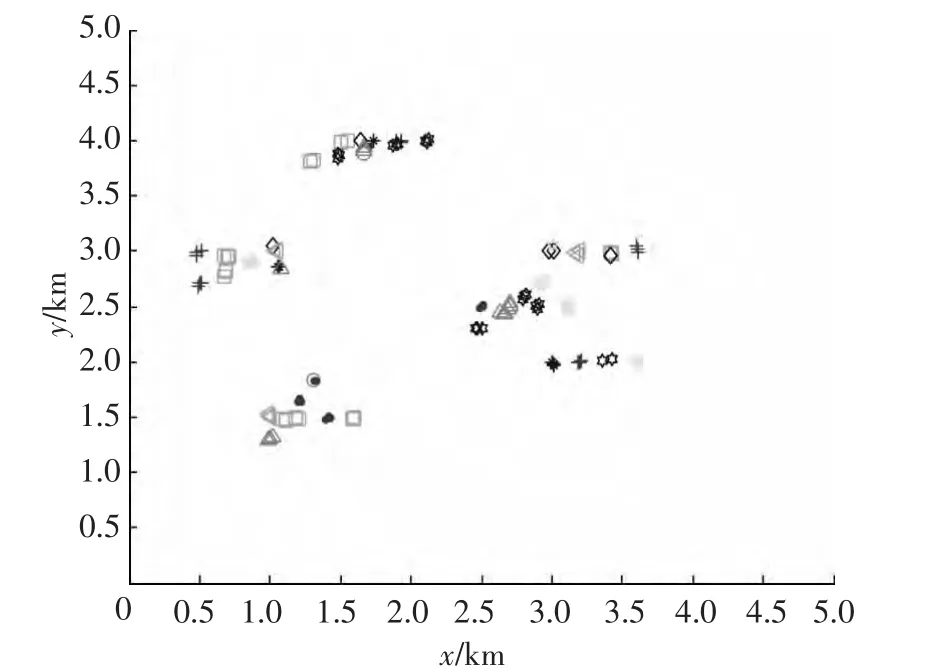
图7 采用标准K-means聚类算法对传感器量测数据分类的结果

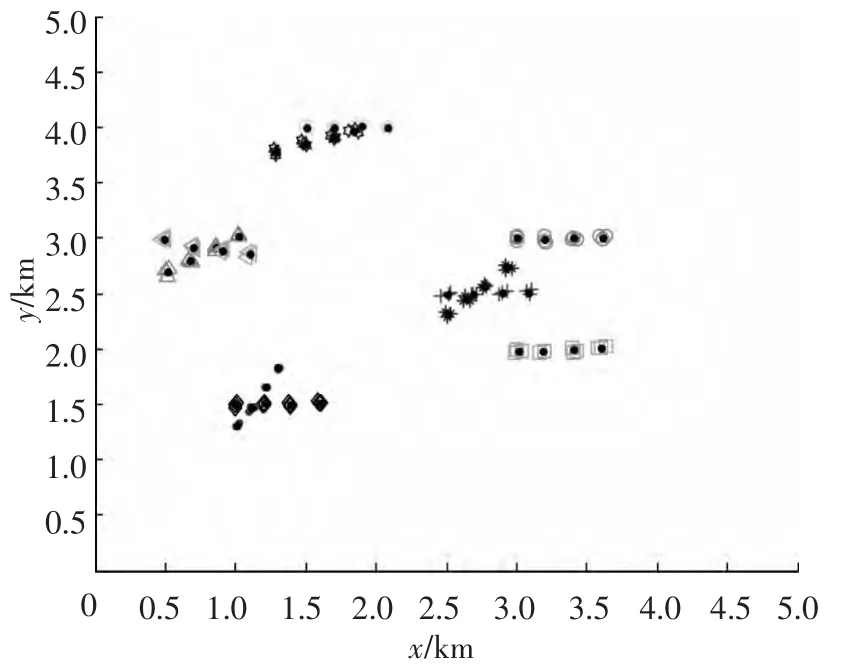
图8 采用本文方法对传感器量测数据分类的结果

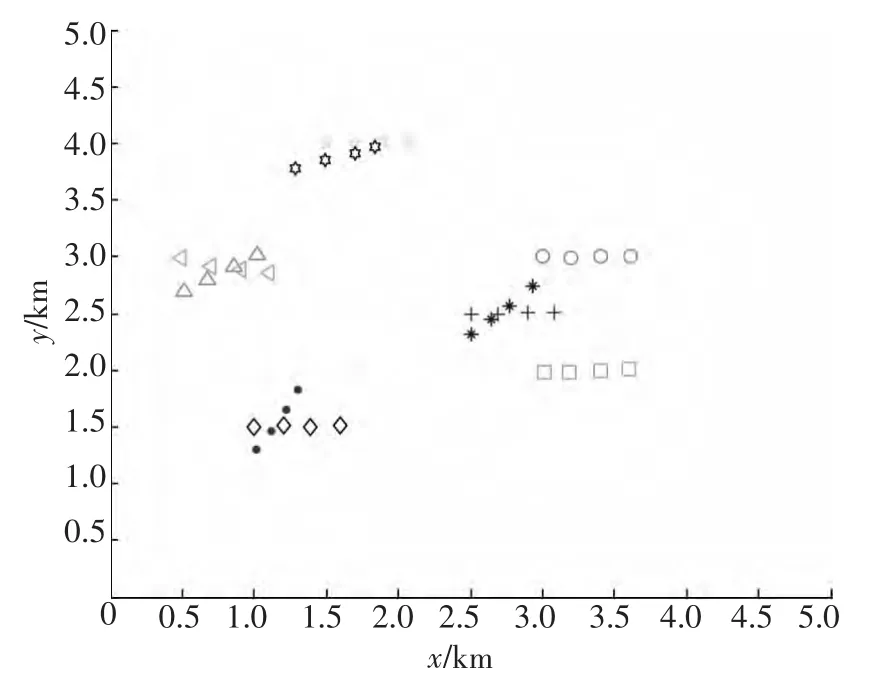
图9 采用本文方法得到的聚类中心

由于在同一时刻来自同一传感器的两观测值实现与同一目标关联是不可能的，故一个聚类中包含的观测值数目应不多于所有传感器观测到的航迹数.

K-means聚类估计的复杂函数为O(nkt)，其中n为整个观测值集合的对象数目，k为最终的聚类数目，t为聚类仿真中的迭代次数.表1对标准K-means聚类算法和本文改进的K-means聚类算法的复杂度和运行时间进行了比较，可知本文改进的K-means聚类算法的复杂度远小于标准K-means聚类算法.

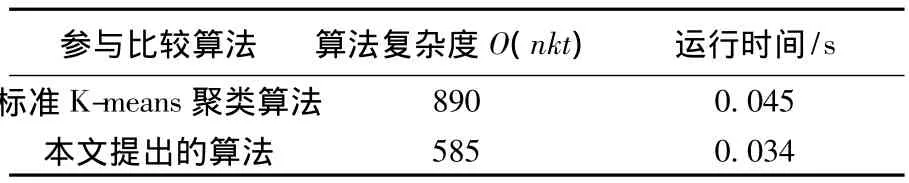
表1 两种聚类算法复杂度和运行时间的比较

综上分析可知，标准的K-means聚类算法由于随机选取初始聚类中心，导致在对观测值进行分类时完全失效了，且聚类结果很不稳定，算法的复杂度也相对较大;作者改进的K-means聚类估计通过自适应的初始聚类中心获取手段，克服了标准K-means聚类估计中必须事先给定类别数k和聚类结果依赖于初始聚类中心这两大缺点，正确识别出目标数，且识别出的目标航迹与真实目标航迹接近，同时算法的复杂度也得到降低，这样就使多传感器系统简化为单传感器估计的情况，也使航迹起始过程大大简化.

3.2 航迹起始过程仿真分析

每个周期的杂波数是根据文献［3］中所述方法按泊松分布确定的，即给定参数λ，首先产生(0，1)区间均匀分布的随机数r，然后由式(1)表示为

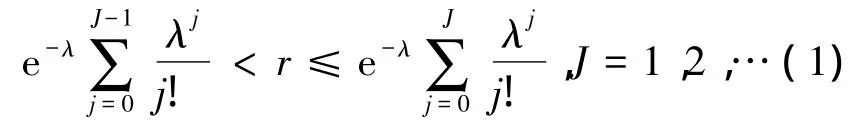
确定出J，则J就是要产生的杂波个数.在确定出J后，每个观测周期的J个杂波按均匀状态分布随机地分布在传感器“视距”区域.

假定λ=50，在连续4个观测周期内获得的杂波点与目标真实点的状况如图10所示.在图10所示观测数据分布态势下，采用本文的改进聚类算法估计获得的聚类结果如图11所示.对图11所示结果按修正的3/4逻辑航迹起始方法进行起始的航迹如图12所示，其中θ=20°;按3/4逻辑法起始的航迹如图13所示;按Hough变换起始的航迹如图14所示，其中Nθ=90、Nρ=90，参数空间的门限取为4;按修正的Hough变换起始的航迹如图15所示，其中:取Nθ=90、Nρ=90，参数空间的门限也取为4.

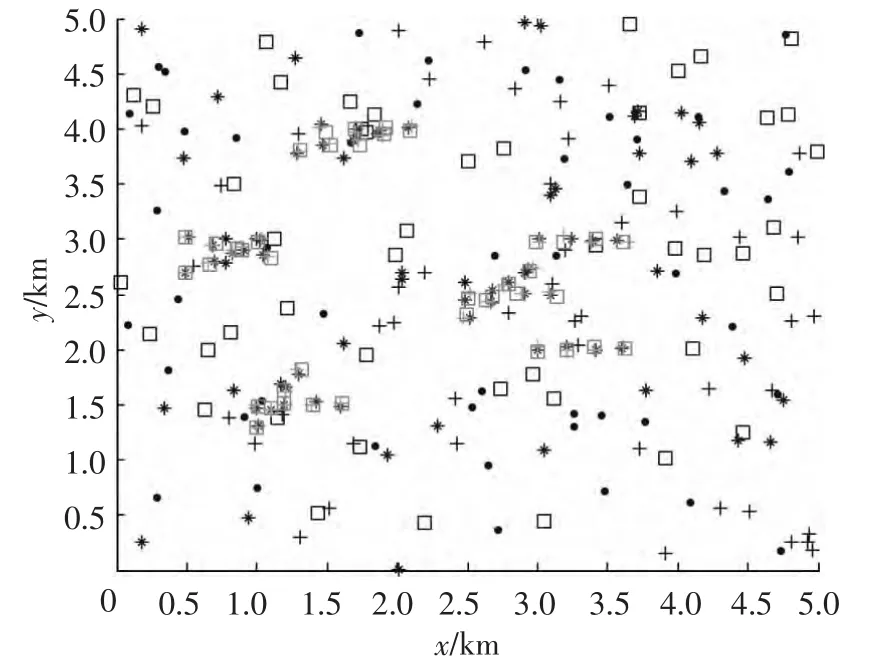
图10 杂波点与真实点的态势图

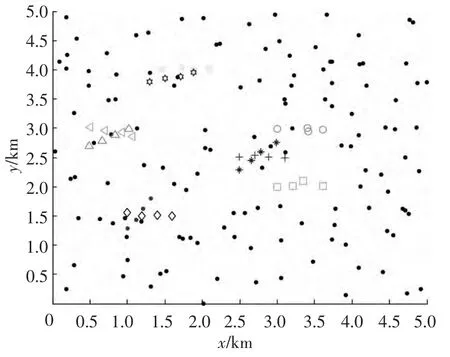
图11 改进K-means聚类算法对杂波和真实点聚类

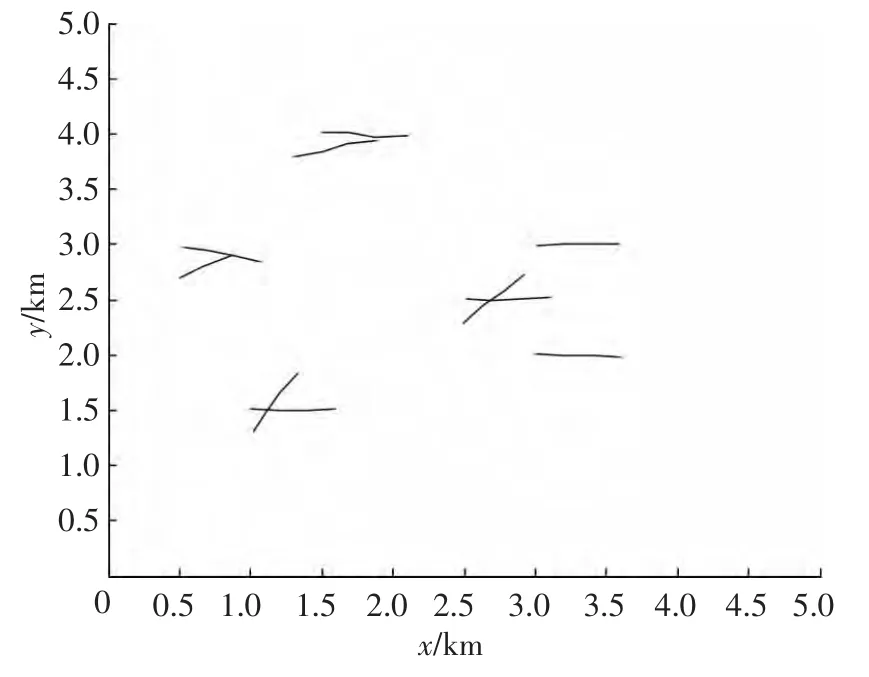
图12 杂波基于修正的3/4逻辑法起始的航迹图

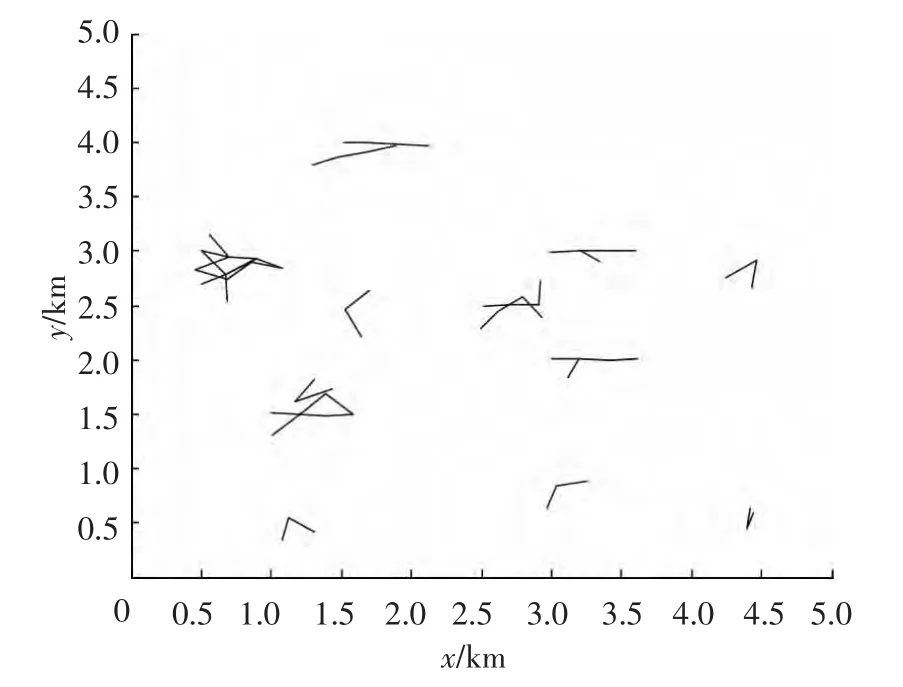
图13 基于3/4逻辑法起始的航迹图

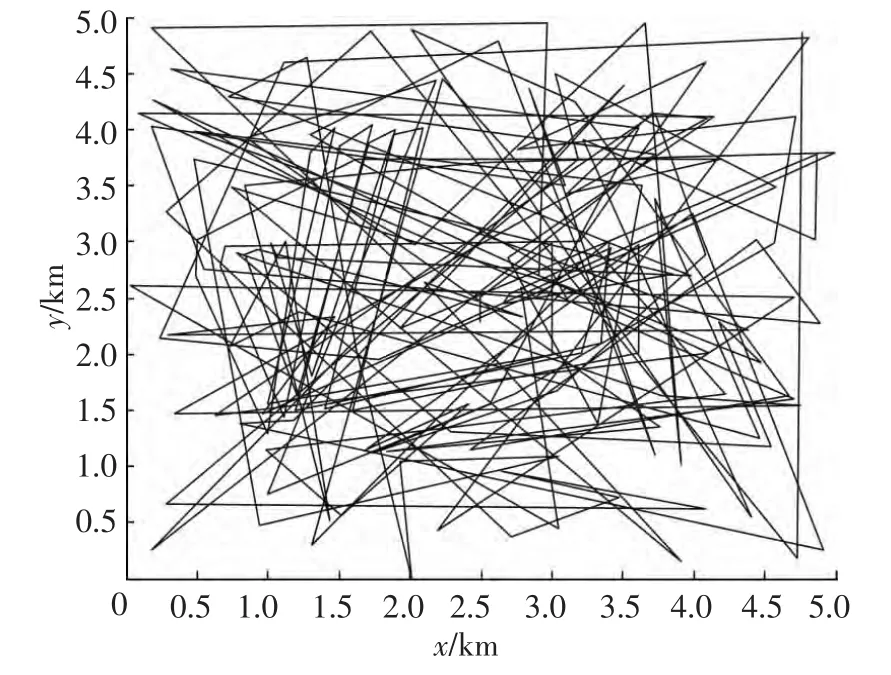
图14 基于Hough变换起始的航迹图

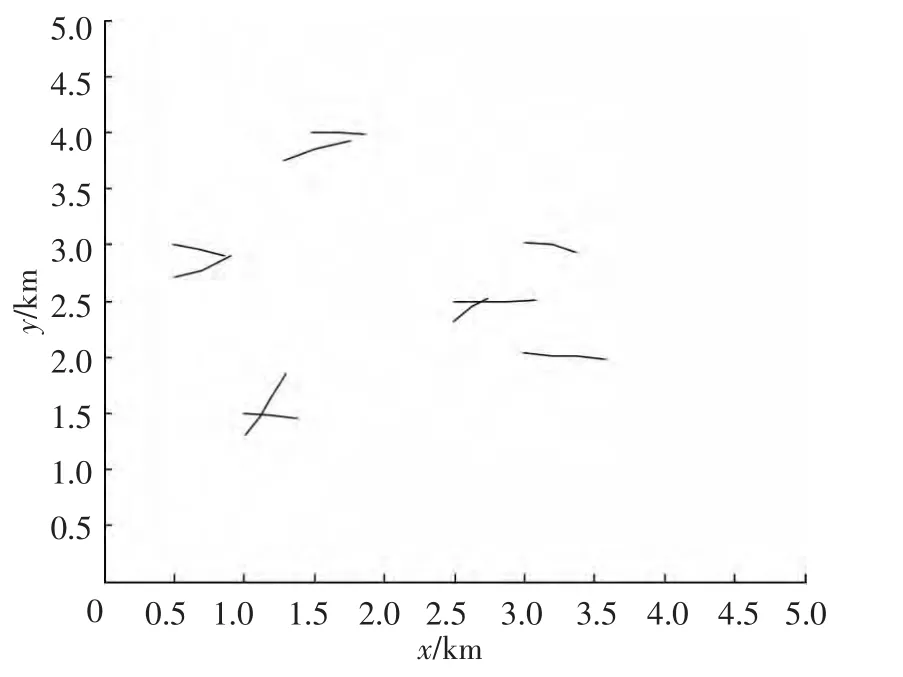
图15 基于修正的Hough变换起始的航迹图

比较图12～15可知，基于Hough变换的航迹起始算法最差，根本不能正确起始目标航迹，基于修正的3/4逻辑法和基于修正的Hough变换法起始的航迹的性能最好，基于3/4逻辑法起始的航迹的性能次之.比较图12、13所示结果知，基于修正的3/4逻辑法航迹起始性能明显优于3/4逻辑法的航迹起始性能.这是因为修正的逻辑航迹起始估计算法采用新增α≤θ的限制条件，确保落入相关波门中的量测应与可能航迹共线，并保证确定航迹中不会存在V字形的航迹.采用该条件可以有效地抑制点迹杂波，降低起始虚警概率.比较图12和15可以看出，基于修正的3/4逻辑法和基于修正的Hough变换法起始的航迹基本一样，这是因为修正的Hough变换和修正的逻辑法一样，都是通过使用速度门限、加速度、角度来进一步剔除虚假航迹.

表2对这4种典型的航迹起始算法的运行时间进行了比较.由表2可知，基于逻辑法的航迹起始时间最短，修正的Hough变换法次之，而Hough变换法的航迹起始时间最长.

表2 4种典型的航迹起始算法运行时间比较 s

综上分析可知，在杂波密度不是很大的环境下，采用修正的逻辑航迹起始算法既可以快速起始航迹，又能有效地抑制杂波，降低虚警概率.

4 结语

针对航迹起始问题，本文应用模式识别理论中的聚类思想，提出一种自适应选取初始聚类中心的K-means聚类算法，对每一时刻各传感器的观测值进行聚类，以区分源于不同目标的数据，并采用修正的逻辑航迹起始算法起始目标航迹.实验结果表明该算法是可行的.自适应K-means聚类估计算法克服了标准K-means聚类估计的缺点，通过基于有效性选择度量两个量测数据不相似性的阈值，能够自适应的选取聚类数目和初始聚类中心，同时降低了算法复杂度，使多传感器系统的航迹起始过程大大简化;采用修正的逻辑航迹起始算法可提高起始航迹速度，还能大幅度抑制点迹干扰杂波，降低航迹起始的虚警概率.

［1］何友，王国宏，陆大纟金，等.多传感器信息融合及应用［M］.北京:电子工业出版社，2010.

［2］张彦航，苏小红，马培军.减法聚类的Hough变换航迹起始算法［J］.哈尔滨工业大学学报，2010，42 (2):264-267.

［3］蒲勇，袁富宇，苗艳.常用航迹初始化技术分析［J］.指挥控制与仿真，2008，28(1):98-101.

［4］吴丹，冯新喜.多雷达多目标航迹起始算法研究［J］.空军工程大学学报:自然科学版，2006，7(1):16-19.

［5］汤琦，黄建国，杨旭东.航迹起始算法及性能仿真［J］.系统仿真学报，2007，19(1):149-152.

［6］金术玲，梁彦，潘泉，等.基于Hough变换和聚类的航迹起始算法［J］.系统仿真学报，2009，21(8):2362-2364.

［7］苏峰，王国宏.修正的逻辑航迹起始算法［J］.现代防御技术，2004，32(5):66-68.

［8］CHEN Xiaowei，LIN Jiajun，ZHANG Jie.Performance analysis of track initiation algorithm［C］//Proceedings of the World Congress on Intelligent Control and Automation (WCICA).Dalian，China:Institute of Electrical and Electronics Engineers Inc，2006:4239-4243.

［9］QING Xiaoping，ZHENG Shijue.A new method for initialising the K-means clustering algorithm［C］//2009 2nd International Symposium on Knowledge Acquisition and Modeling(KAM，2009).Wuhan，China:IEEE Computer Society，2009:41-44.

［10］SHI Na，LIU Xumin，GUAN Yong.Research on K-meansclusteringalgorithm:an improved K-means clustering algorithm［C］//3rd International Symposium on IntelligentInformation Technology and Security Informatics(IITSI 2010).Jinggangshan，China:IEEE Computer Society，2010:63-67.

［11］WILKIN G A，HUANG Xiuzhen.K-means clustering algorithms:implementation and comparison［C］// Proceedings-2nd International Multi-Symposiums on Computer and Computational Sciences(IMSCCS'07). Iowa City，IA，United states:Inst of Elec and Elec Eng Computer Society，2007:133-136.

［12］周士兵，徐振源，唐旭清.K-means算法最佳聚类数确定方法［J］.计算机应用:2010，30(8):1995-1998.

［13］周武，赵春霞，张浩峰.动态联合最近邻算法［J］.电子学报:2010，38(2):359-365.

［14］REUTER S，DIETMAYER K.Adapting the state uncertaintiesoftracksto environmentalconstraints［C］//13th Conference on Information Fusion(Fusion 2010).Edinburgh，United Kingdom:IEEE Computer Society，2010:1-7.

［15］SONG T L，MUSICKI D，SOL K D.Target tracking with targetstate dependentdetection［J］.IEEE Transactions on Signal Procession，2011，59(3): 1063-1074.

［16］WILLIAM N G，JACK L I，SIMON G，et al. Multitarget initiation，tracking and termination using bayesian monte carlo methods［J］.The Computer Journal，2007，50(6):674-693.

［17］SONG T L，SICKI D M.Adaptive clutter measurement density estimation for improved target tracking［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47(2):1457-1466.

［18］TURNER E L.Firm track loss due to M of N track initiation of a radially inbound target［C］//IEEE International Radar Conference 2010(RADAR 2010). Washington DC，United states:Institute of Electrical and Electronics Engineers Inc，2010:1250-1254.