双目立体视觉的无人机位姿估计算法及验证

张 梁，徐锦法，夏青元

(南京航空航天大学直升机旋翼动力学国家级重点实验室，210016南京)

导航在无人机自主飞行中具有关键作用，大多采用惯导、GPS、天文、多普勒等方式实现，也有采用激光、红外与超声波等测距方式实现.惯性导航与GPS组合是目前应用最为广泛的导航方式.尽管如此，由于GPS借助卫星定位，受地形干扰及人为控制，天文及多普勒导航方式亦如此.激光、红外等测距设备虽然测量精度高，但由于自重较大，也不宜应用于微小型无人机.随着计算机技术发展，视觉技术发展迅速，近年来各国均已开展深入研究，因其导航方式不受地形天气等因素干扰而得到广泛重视［1-3］.

无人机视觉导航摄像头可用下视方式或前视方式采集图像信息.下视安装方式已在无人机视觉导引着陆中得到成功应用，文献［4］就是用下视方式安装摄像头，应用单目视觉摄像机实现了微型四旋翼飞行器的自主着陆导引.前视方式也有成功应用实例，通过安装前视摄像头使微小型无人机在城市环境甚至室内环境中具有自主飞行能力，发挥交通监控、目标跟踪、火灾监测等重要作用.文献［5］是前视方式安装摄像头的应用案例，应用立体视觉和光流算法实现了无人直升机的自主飞行控制系统，并进行了地面试验验证.

单目视觉、双目视觉或多目视觉可以估计飞行器的位姿信息，由于单目视觉无法得到目标物体的深度信息，就难以得到全部位姿信息，而双目视觉可以得到摄像机坐标系下的目标物体三维坐标，通过位姿估计能快速导引无人机飞行.文献［6-8］采用双目立体视觉技术完成了视觉里程计设计，并与GPS等其他导航技术融合实现了无人运载车辆地面运动控制.

近年来，国内在无人机视觉导航方面也开展了深入研究.文献［9］提出了基于特定标志的无人机视觉导引着舰方案，文献［10］提出了在机场跑道安装红外导引标志的视觉导航方法.尽管研究进展卓有成效，但实际应用中具有一定的局限性，因为这两种方案均需特定导引标志，只局限于导引着陆.文献［11］提出了立体视觉与惯性导航相融合的组合导航方法，但侧重于组合导航方式探讨，还未进行实际应用研究.

本文运用视觉里程计概念，提出了基于双目视觉的无人机运动位置和姿态的计算方法.双目立体摄像机能得到两组立体图像序列，通过提取相匹配的特征点，经运算得到同一时刻摄像机坐标系下的特征点坐标值，再利用前后两时刻相匹配的特征点坐标值得到无人机运动位置和姿态的估计值，进而实现无人机运动控制.

1 摄像机模型及坐标系关系

摄像机模型决定了空间物体某点与图像平面一点的对应关系，这一几何模型的参数称为摄像机参数，可通过实验和计算得到，即标定［12］过程.标定的目的是得到摄像机参数，包括内参与外参，内参只与摄像机内部结构有关，外参由摄像机与世界坐标系关系决定，具体参数可见式(1).摄像机模型不仅可用于校正摄像机畸变，还可用于摄像机运动轨迹估算.现以针孔摄像机模型为例进行说明.

摄像机模型涉及的坐标系如图1所示，摄像机坐标系为Xc-Yc-Zc，图像坐标系为u-v，Xc轴与u轴平行，Yc轴与v轴平行，Zc轴与光心重合，便于图像坐标与摄像机模型坐标转换.

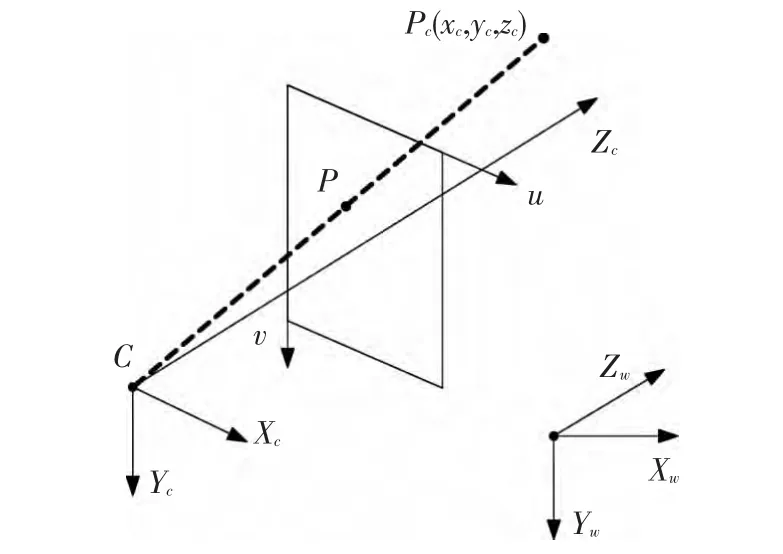
图1 各坐标系间关系

根据透视投影关系，基本针孔摄像机模型的空间任意一点P与图像平面对应关系可表示为

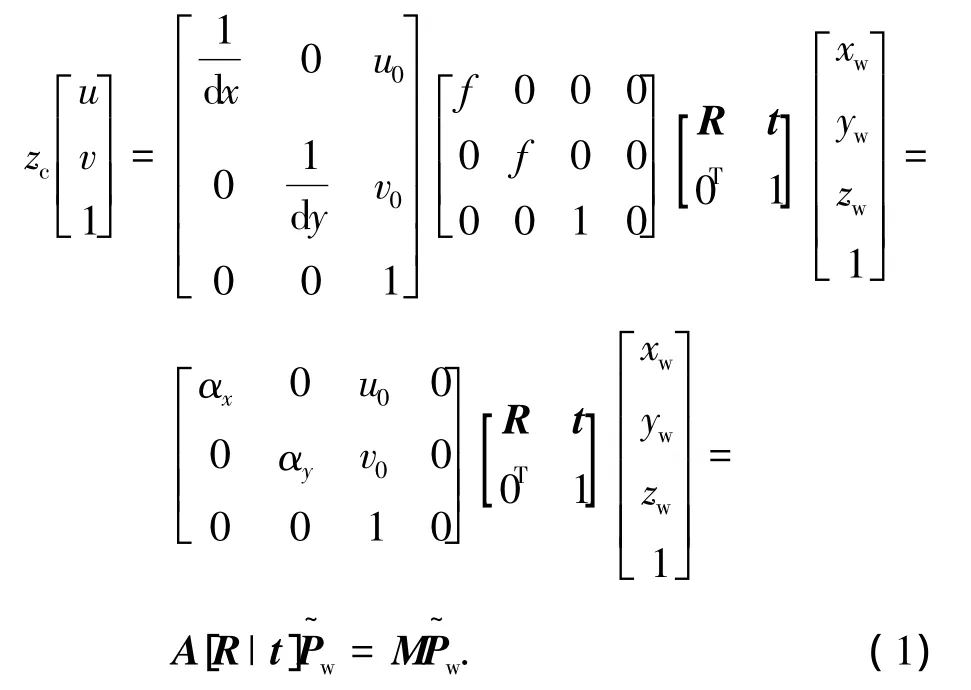
式中:zc是摄像机坐标系下Z轴坐标;u、v是图像坐标系下像素坐标值;dx、dy是图像坐标系下每一个像素在x轴和y轴方向的物理尺寸，单位为mm;u0、v0是摄像机光轴与图像平面的交点坐标值;f是摄像机焦距;R、t分别是世界坐标系相对于摄像机坐标系的旋转矩阵和平移向量;xw、yw、zw分别是该特征点在世界坐标系下坐标值;αx= f/dx、αy=f/dy;M称为投影矩阵，而A和［R｜t］分别称为摄像机的内参和外参，上标 ～表示齐次向量.

本文通过双目相机采集图像，定义左相机坐标系为基准参考坐标系.相机经过标定，所采集图像均经过了畸变校正以及双目立体校正［13］.

2 特征点提取与匹配

应用较广泛的特征点提取算法有Harris算法、SUSAN算法、SIFT算法及其各种衍生算法. Harris算法和SUSAN算法基于灰度匹配，而SIFT算法基于特征匹配.SUSAN算法简单、实时性好，但是精度相对差;SIFT算法基于图像特征实现匹配，精度相对高，但是计算较复杂，实时性差; Harris算法居于两种算法之间，兼顾了实时性与精度要求，因此本文采用Harris算法［14-15］作为特征点提取算法.

本文所采集图像分辨率大小为640×480，结合Matlab的CornerDetector工具箱实现特征点提取，相比Harris算法计算流程，设置相对简单.角点提取过程中阈值设置为0.000 02，采用13×13窗口进行局部最大值搜索操作，保留具有最大特征值的特征点，使得特征点分布相对分散，提高特征点匹配准确度，由此每幅图像可得到大约430个特征点.

图像特征点提取后，左右视图特征点如何匹配是进行摄像机三维重建的关键，前后帧图像特征点匹配是实现位姿估计的前提.

运动估计需要前后时刻左右相机共4幅图像进行匹配，以此作为一个运动估计周期内的特征点集.因此，首先进行当前时刻左右图像特征点匹配，以左图像上的特征点为基准，寻找右图像上对应的特征点，从而得到匹配点集.由于左右图像经过立体校正，实现了行对准，左右视图匹配过程中对应特征点搜索范围可限制在横轴上，减小搜索时间.之前时刻左右图像的特征点匹配方法相同，从而得到之前时刻左右相机匹配点集.得到这两个匹配点集之后，在这两个匹配点集中寻找前后时刻左相机中相匹配特征点，同样以当前时刻左图像上的特征点集为基准，寻找之前时刻左图像上的匹配特征点，从而得到匹配点集，相当于求得了当前时候与之前时刻两匹配点集的交集.由此可得到一个运动估计周期内4副图像的初始匹配特征点集.

图像中特征点匹配采用归一化互相关［16］(NCC)实现，基于特征点周围灰度信息，计算特征点灰度相关系数，相关系数值越大，匹配度越高.对灰度值及其方差的平均化处理能消除光照变化的敏感性.选定待匹配图像中特征点，以特征点为中心建立(n+1，n+1)窗口W，则两特征点归一化互相关系数可表示为

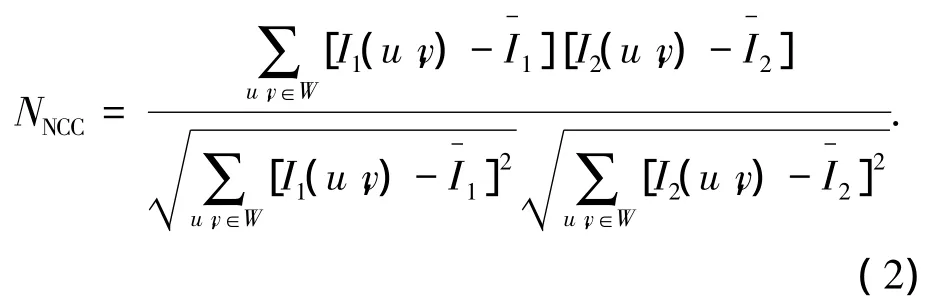
式中:I1、I2分别表示两窗口内图像灰度值分别表示窗口中像素灰度平均值.

运用 Matlab/matchfeatures工具箱能快速实现NCC特征点匹配计算.NCC矩形窗大小选择25×25.工具箱中阈值设定越低精度越高，但是匹配点相对较少，因此通过实验设定阈值为13.经过4幅图像的匹配之后，最终得到约100个匹配特征点集，作为位姿估计的初始匹配点集.

3 特征点三维重建

立体视觉方法获取二维图像，能实现三维几何形状物体重建［17］，即由得到的摄像机坐标系下物体特征点三维坐标值可实现摄像机位置和姿态估计.如图2所示，假定两摄像机内参相同，且两坐标系仅在x轴相差一段距离B，即基线距离，公共视场空间点P(xc，yc，zc)在左右摄像机坐标系下坐标分别为P(xc，yc，zc)和P(xc-B，yc，zc)，对应特征点在两图像平面内的坐标为pL(uL，vL)、pR(uR，vR)，由于图像经过立体校正，故有vL=vR.

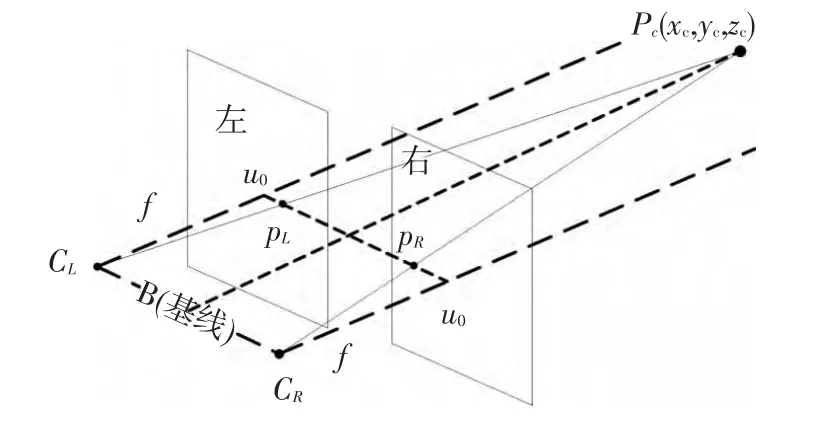
图2 双目视觉图像重建示意

由图2可知，根据相似三角形原理以及摄像机投影方程公式，可得如下关系:

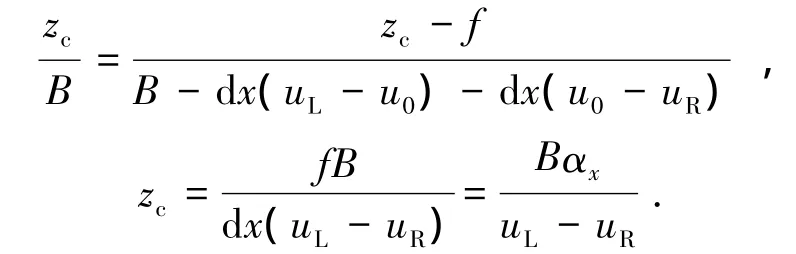
根据摄像机投影方程

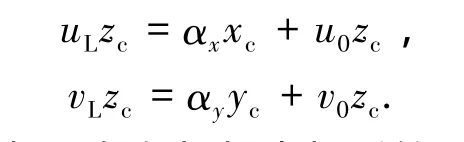
可得到空间点P在左相机坐标系的三维坐标为

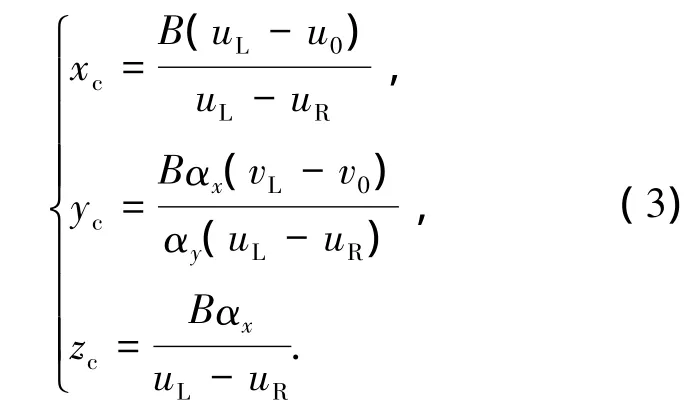
据此，由左、右像平面的pL和pR坐标可计算得到空间点P在摄像机坐标系内三维坐标值，实现特征点三维重建.

4 运动位姿估计

单目摄像机能用前后帧图像计算姿态变化，但由于缺少深度尺度因子，不能仅凭摄像机计算得到位置变化，需要其他传感器辅助，而双目摄像机能得到特征点深度信息，就可凭双目摄像机得出位置和姿态变化，优势明显.双目视觉图像经图像处理、特征点提取及匹配后可得到一组特征点集，利用特征点集就能计算出坐标变换旋转矩阵和平移向量.

如图3所示，以左摄像机为基准，摄像机坐标系下前后时刻对应特征点关系为

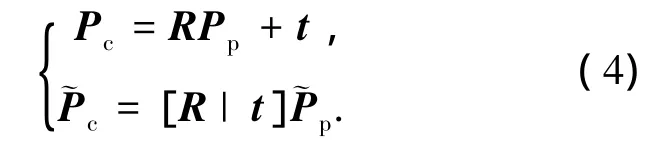
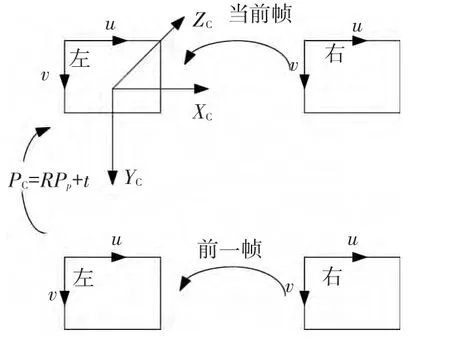
图3 立体视觉位姿估计示意

式中:Pc表示当前帧中任意特征点的摄像机坐标系三维坐标值;Pp表示前一帧中与当前帧对应特征点的摄像机坐标系三维坐标值;上标 ～表示齐次向量;R、t分别表示摄像机坐标系旋转和平移量.

由式(4)可知，定义如下性能代价函数:

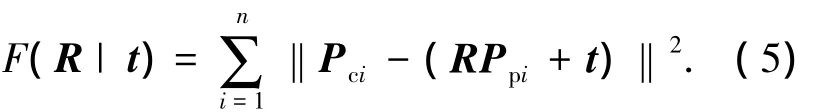
运用最小二乘法原理可求解得到旋转和平移量.旋转矩阵R是单位正交矩阵，需满足、i=1，2，3、j=1，2，3且i≠j.由此可知，上述代价函数并非简单线性方程，不能使用线性最小二乘通用方法求解.

由于代价函数的非线性特性，为求解带约束代价函数，通常应用拉格朗日乘子法将代价函数与约束条件相结合［17］，通过3个或4个特征点，利用奇异值分解法求解旋转与平移量.本文采用L-M迭代算法［12］进行迭代求解.旋转矩阵R可用欧拉角表示，如式(6)所示，代价函数中变量转换为欧拉角.

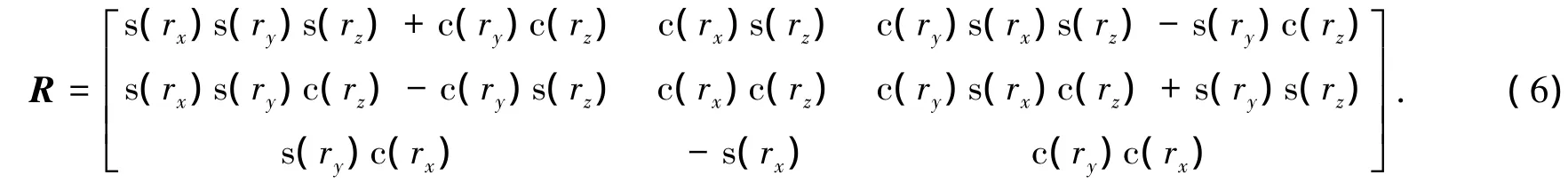
式中s表示sin，c表示cos，rx、ry、rz分别表示欧拉角.

L-M算法是一种迭代求解法，能有效求解非线性最小二乘问题，利用该方法可以选择相对精确的估计初值，有效降低迭代次数.通过调用L-M算法，可以省去矩阵奇异值分解等操作，即使R、t初值取值I、0也可快速实现收敛.实验发现，迭代次数不需超过10次即可得到较为精确的初步结果.

随机 抽 样 一 致 算 法 (random sample consensus，RANSAC)［12］能有效实现野值和内点集的区分，具体步骤为:1)随机选择最小特征点集;2)确定模型估计参数;3)计算满足设定阈值ε的特征点数量;4)重复1)至3)步骤N遍，选取满足阈值的具有最多特征点的那次估计作为最大内点集.应用RANSAC算法，结合代价函数计算，得到具有最大内点集的旋转与平移量，以此作为位姿估计的迭代初始值，再用L-M迭代算法得到相对精确的旋转与平移量.

确定一个平面至少需要3个特征点，应用RANSAC算法随机选取3个特征点，收敛精度选为ε=10-6，用L-M迭代算法计算代价函数，设定RANSAC距离阈值为2个像素，超过距离阈值即被认为外点，反之则为内点.用RANSAC算法重复计算20次，得到具有最大内点集的R、t.再利用最大内点集进行迭代计算，最大内点集的R、t作为迭代初值，继续进行L-M迭代计算，收敛精度为ε=10-8，最终得到R、t.

利用前后帧图像仅能得到前后时刻的相机相对位置，无法得到相对于世界坐标系的相机位置.要想得到相对于世界坐标系的相对位置，需建立摄像机坐标系与世界坐标系之间的对应关系.设定摄像机起始时刻的位置，找出摄像机在任意时刻与起始时刻的对应关系，即可得到任意时刻摄像机在世界坐标系中的位置.

由式(4)可得出某一特征点在任意k时刻可表示为

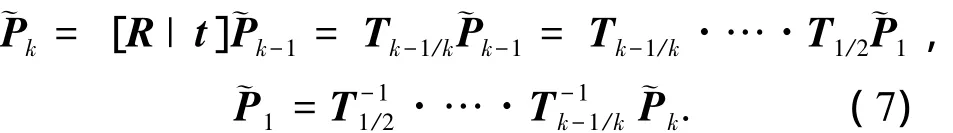
根据摄像机标定有

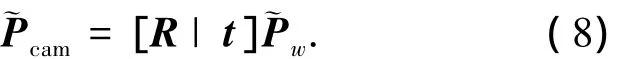
由此可导出~P1=［R0｜t0］~P1w=T1~P1w，其中~Pcam为特征点在摄像机坐标系下坐标值，R0、t0由标定得到.若世界坐标系与摄像机坐标系的起始帧位置一致，则取R0=I、t0=0代入式(7)得

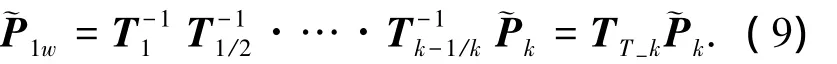
式中TT-k即表示任意k时刻摄像机与世界坐标系之间的旋转与平移量.

TT-k中的t向量为世界坐标系下三轴位移量(tx，ty，tz)，三轴线速度由k时刻与k-1时刻位移量差值得到

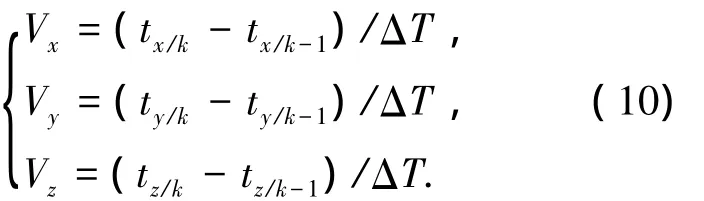
式中ΔT表示两帧图像之间采样间隔.

飞行器姿态角定义为机体坐标系与世界坐标系间相对角度，对TT-k取逆即为旋转矩阵R的欧拉角，即

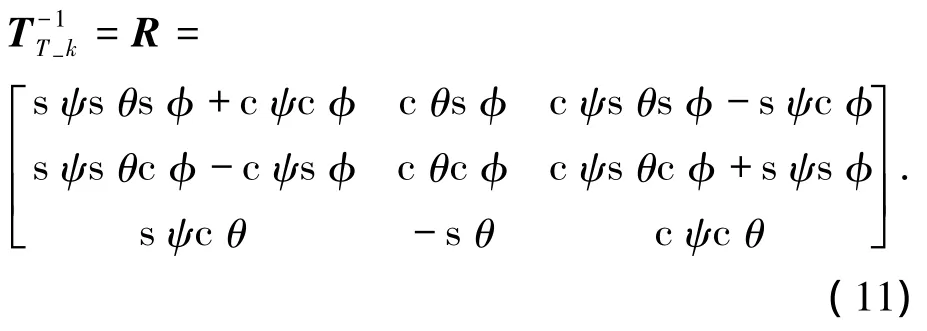
式中θ为俯仰角，ψ为偏航角，φ为滚转角.由旋转矩阵对应元素可得出姿态角，即

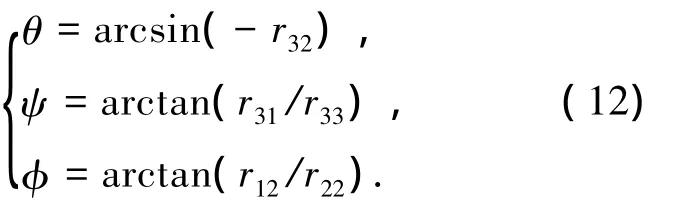
5 实验与结果

为验证前述视觉图像处理算法和位姿估计算法的正确性，应用PointGray公司Bumblebee2立体视觉摄像机设备进行了位姿估计验证实验. Bumblebee2采用3.8 mm焦距Sony镜头，具有65°水平视场(HFOV)，采用CCD感光元件，曝光形式为整帧曝光，最大分辨率下具有20FPS帧率. Bumblebee2设备精度高，且标定参数已知，如表1所示.依据前述图像处理算法和位姿估计算法，用C语言和m语言在Matlab环境下编程实现.本文在实验室环境进行了一系列图像采集和处理，把相应算法和软件应用于微小型无人机以验证算法的正确性和可行性.

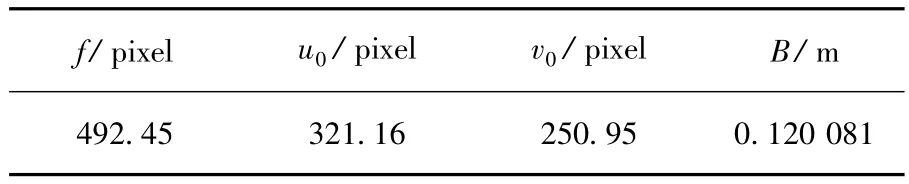
表1 Bumblebee2图像标定参数(640×480)

位姿估计算法流程如图4所示，以离线方式完成图像序列位置和姿态估计.

由于算法处于验证阶段，实验环境为工作室室内环境，光照条件固定，易于实现算法验证.实验采用固定相机方法，将相机固定于三脚架之上，保持相机静止，连续采集80帧立体图像，帧间隔为0.2 s，所采集图像像素大小为640×480，图像均经过畸变校正与立体校正，图5所示为立体图像的特征点检测与匹配样例.

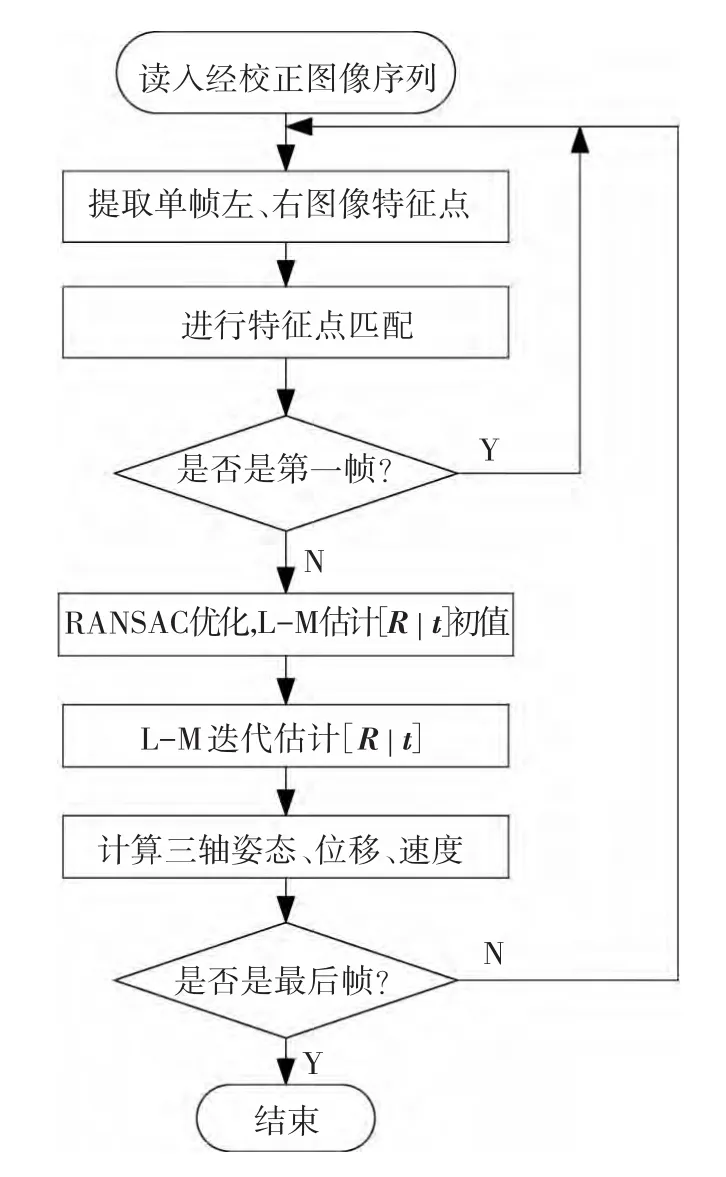
图4 位姿估计计算流程

图5 立体图像特征点检测与匹配

位姿估计采用前述迭代算法计算得到，且累积误差能控制在较小的范围内，如图6所示为实验采集到图像的静态偏移测试结果，图7为实验得到的姿态估计结果.图中所标示的设定值是用AP800电子螺距尺测量得到的姿态角.实验时相机固定于三脚架上，手动移动云台，同时记录螺距尺上显示数据.图像数据帧之间的间隔时间为0.2 s，共采样80帧立体图像.由图可知，位姿估计值与设定值偏差较小，角度误差小于3°，偏航角与俯仰角仅在设定值变化阶段有较大误差，这与视场变化时特征点匹配计算误差有关，摄像机自身变化过快，影响相邻图像帧匹配特征点的精确寻找.滚转角误差相对大些.

图8为位置估计结果，实验时手持相机沿工作室小隔间隔板运动，采集图像后进行运动轨迹估计.图像数据帧之间的间隔时间为0.2 s，共采样170帧立体图像.工作室隔间长1.2 m，宽0.8 m，估计得到的运动轨迹与此尺寸相符，图中所示轨迹与X轴和Z轴均存在夹角是因为起始位置与隔间隔板存在夹角.

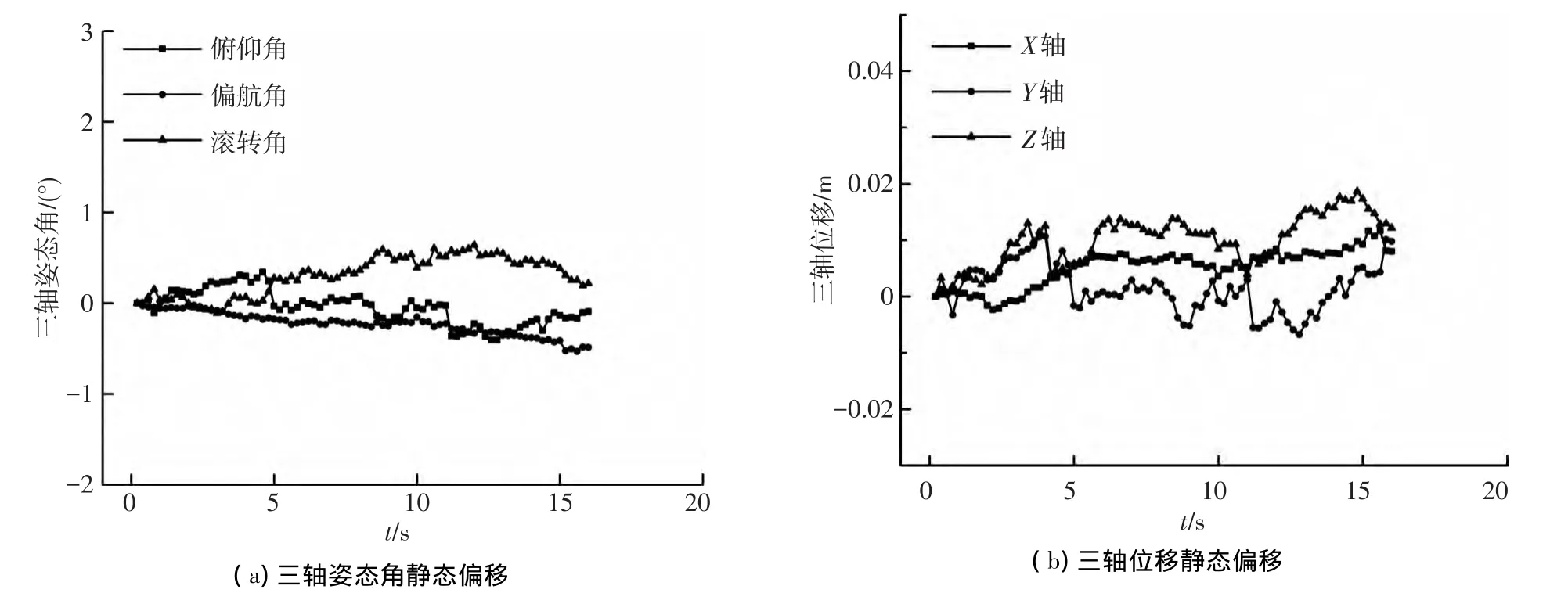
图6 静态偏移测试

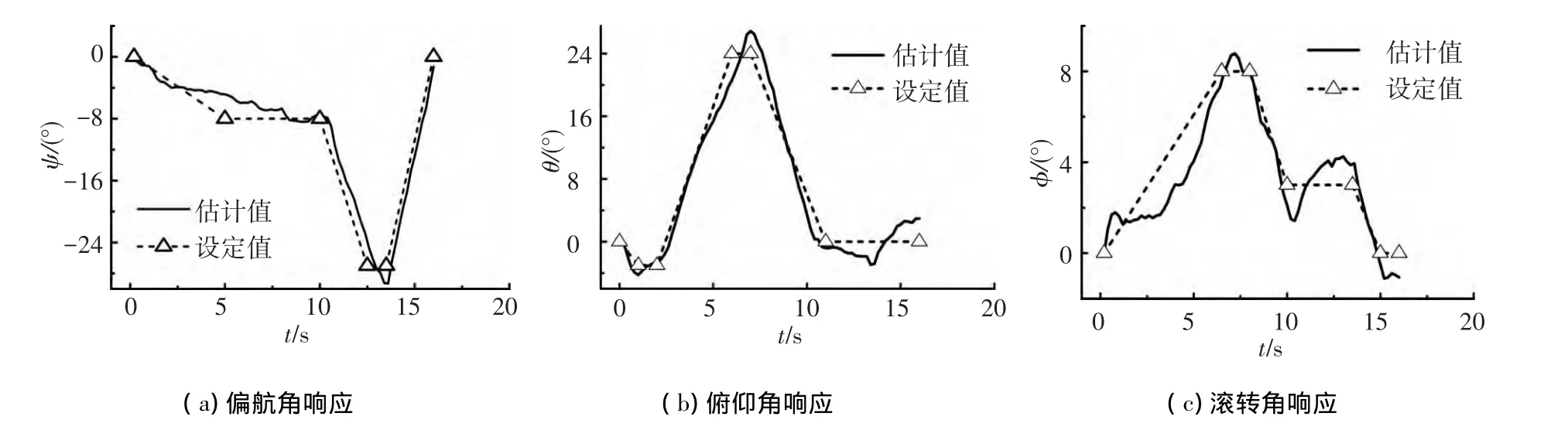
图7 姿态角响应过程

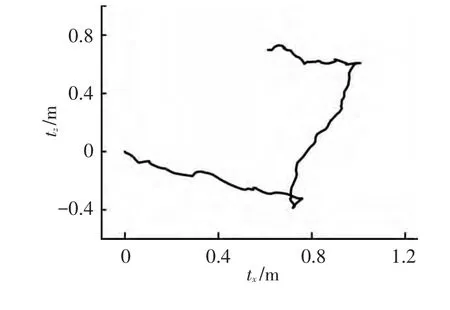
图8 平移运动轨迹

6 结 语

基于立体视觉估计无人飞行器的位置和姿态是无人飞行器导航系统的关键环节，以双目摄像机为实验设备，应用视觉里程计原理能实现双目摄像机的标定、立体图像校正、特征点提取与匹配、摄像机位置和姿态估计，为无人飞行器的导航提供了一条新的技术途径.

双目视觉图像可得到物体立体信息，利用图像处理得到的特征点集可估计出无人飞行器的位置和姿态，可使飞行器不依赖于特定的导引标志实现未知复杂环境下的自主导航.实验结果表明位姿估计误差较小，能满足导航需求.

［1］JOHNSON E N，CALISE A J，WATANABE Y，et al. Real-time vision-based relative aircraft navigation［J］. Journal ofAerospace Computing，Information，and Communication，2007，4(4):707-738.

［2］SATTIGERI R J，CALISE A J，KIN B S，et al.6-DOF nonlinear simulation of vision-based formation flight［C］//AIAA Guidance， Navigation， and Control Conference and Exhibit.Reston VA:AIAA，2005，DOI: 10.251416.2005-6002.

［3］DE WAGTER C，BIJNENS B，MULDER J A.Visiononly control of a flapping mav on mars［C］//AIAA Guidance，Navigation and ControlConference and Exhibit.Reston VA:AIAA，2007:AIAA2007-6853.

［4］KENDOUL F，NONAMI K，FANTONI I，et al.An adaptive vision-based autopilot for mini flying machines guidance，navigation and control［J］.Autonomous Robots，2009，27(3):165-188.

［5］HRABAR S，SUKHATME G S，CORKE P，et al. Combined optic-flow and stereo-based navigation of urban canyons for a UAV［C］//IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS). Edmonton，Alberta:［s.n.］，2005:3309-3316.

［6］LATEGAHN H，DERENDARZ W，GRAF T，et al. Occupancy grid computation from dense stereo and sparse structure and motion points forautomotive applications［C］//Intelligent Vehicles Symposium (IV).Piscataway:IEEE，2010:819-824.

［7］KITT B，GEIGER A，LATEGAHN H.Visual odometry based on stereo image sequences with RANSAC-based outlierrejection scheme［C］//IntelligentVehicles Symposium(IV).Piscataway:IEEE，2010:486-492.

［8］AGRAWAL M，KONOLIGE K.Real-time localization in outdoor environments using stereo vision and inexpensive GPS［C］//International Conference on Pattern Recognition.Piscataway:IEEE，2006，3:1603-1608.

［9］潘顺良，王晓剑，沈为群，等.视觉导引的无人直升机自主着舰系统仿真［J］.航天控制，2008，26(2): 63-67.

［10］徐贵力，倪立学，程月华.基于合作目标和视觉的无人飞行器全天候自动着陆导引关键技术［J］.航空学报，2008，29(2):437-442.

［11］李建，李小民，钱克昌，等.基于双目视觉和惯性器件的微小型无人机运动状态估计方法研究［J］.航空学报，2011，32(11):2310-2317.

［12］HARTLEY R，ZISSERMAN A，EBRARY I.Multiple view geometry in computer vision［M］.Cambridge: Cambridge Univ Press，2003:151-361.

［13］FUSIELLO A，TRUCCO E，VERRI A.A compact algorithm for rectification of stereo pairs［J］.Machine Vision and Applications，2000，12(1):16-22.

［14］GONZALEZ R C，WOODS R E.Digital image processing［M］.San Antonio，TX:Pearson Education，2002:399-550.

［15］HARRIS C，STEPHENS M.A combined corner and edge detector［C］//Procedings of Fourth Alvey Vision Conference.Manchester，UK:［s.n.］，1988:147-151.

［16］TSAI D M，LIN C T.Fast normalized cross correlation for defect detection［J］.Pattern Recognition Letters，2003，24(15):2625-2631.

［17］马颂德，张正友.计算机视觉:计算理论与算法基础［M］.北京:科学出版社，1998:282.