基于联合对角化的近场源三维参数估计∗
王 超,魏玺章
(国防科技大学电子科学与工程学院,湖南长沙410073)
0 引言
空间信源定位是阵列信号处理中的一项重要研究内容,一直受到国内外学者的密切关注。早期的空间信源定位研究主要集中在远场源的DOA估计上面,然而当信源靠近阵列而处于阵列的Fresnel区(近场区)[1]时,波前的固有弯曲将不能忽略,即远场平面波前的假设将不再成立,需要用球面波来精确描述,其形状随阵元位置具有非线性变化特性,可以通过信源的距离及其DOA来联合确定,当信源的频率未知时,近场源参数估计就成了频率、距离和DOA的联合估计问题。近场源定位在语音增强、声源定位、雷达[2]、声纳、电子监测和地震监测等领域中具有广泛的应用。
近年来,人们提出了许多近场源距离和DOA等多参数联合估计问题[3-12],文献[3]最早提出了最大似然估计方法,该方法具有最优的估计性能,但需要多维搜索并且是高度非线性的。Huang等人[4]和Russell等人[5]把传统的一维MUSIC算法推广到二维MUSIC算法,实现距离和DOA的联合估计,但是二维MUSIC算法仍然要作复杂度很大的二维搜索。Starer等人[6]提出的路径跟踪(path-following)进一步降低了二维MUSIC的运算量。为避免多维搜索,Challa和Shamsunder[7]提出了一种基于四阶累积量矩阵的类ESPRIT方法,该方法理论上不需谱峰搜索且各参数自动配对,但由于二维参数分别由独立的特征分解得到,所以实际上仍需要参数配对,而且阵元利用率较低。基于四阶累积量的改进的MUSIC算法[8]也被提出,利用高阶累积量带来的虚拟阵元扩展和抑制色噪声的作用,提高了传统MUSIC算法的效率,但仍然需要非线性的多维搜索。Emmanuele和Karim[9]提出了一种加权线性预测方法,需要解多个约束最优化方程和参数配对问题。陈建峰[10]、黄家才[11]和梁军利[12]等人提出了基于高阶累积量的频率、距离和DOA联合估计方法,通过选择特定序号阵元输出来构造多个特定结构的高阶累积量,并利用不同累积量矩阵的结构关系来获得待估计的参数,算法由于进行了多次特征分解导致需要进行参数匹配,或者是利用了线性阵列的对称性而造成了孔径损失。周祎[13]和胡增辉[14]利用联合对角化在假设信源频率已知时估计近场源距离和DOA时取得了一定的效果。
上述分析显示在近场源定位场景中存在的问题主要集中在以下三个方面:(1)阵列孔径的损失;(2)估计参数的配对;(3)需要计算量较大的搜索或者迭代运算;(4)信号源频率、DOA、距离等多参数的联合估计。为了克服上述缺点,本文提出了一种近场源信号频率、到达角和距离的联合估计算法,将联合对角化方法用于近场源频率、距离和DOA估计,首先基于阵列接收数据的协方差矩阵构造白化矩阵,再利用一组累积量矩阵的对角结构信息和联合对角化矩阵得到阵列流形和信号源频率的估计,进而由阵列导向矢量联合对应的信号源频率估计信号源的到达方向和距离。与基于四阶累积量的类ESPRIT方法相比,本文所提算法能够联合估计频率、到达角和距离,并且提高了阵元利用率,避免了参数匹配操作。
1 信号模型
假定有M个近场窄带信号源入射到间距为d的均匀线阵(如图1)上,且均匀线阵由2N+1个阵元构成,从左至右阵元编号为-N,-N+1,…,0,…,N-1,N,中心阵元为编号为0的参考阵元,源信号经过解调到中频并抽样后,第m个源信号可表示为S m(t)=s m(t)ejωmt,s m(t)表示信号的复
包络,ωm为信号频率。故第l个阵元上的接收信号可表示为
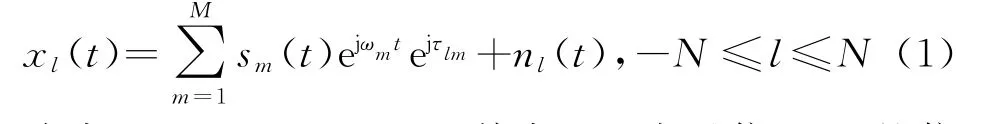
式中,s m(t)=A mejφm,其中A m表示信源m的信号幅度,φm表示信源m的初始相位,n l(t)是阵元l接收到的加性复高斯白噪声,用τlm表示第m个信源在阵元l和参考阵元0之间的相位差,可以表示为
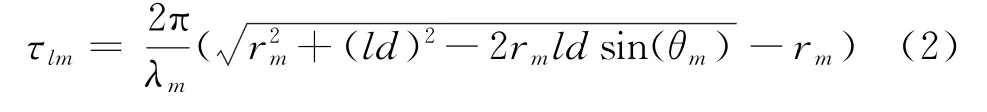
式中,λm,θm,r m分别为信源m的波长、DOA和距离;d为均匀阵列阵元间距;f m=c/λm为信源m的中心频率。如图1所示,为避免模糊假设信源DOA满足-π≤θm≤π/2。
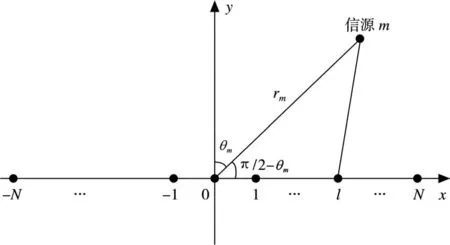
图1 均匀线阵近场源结构示意图
利用近场源近似即Fresnel近似(本质为Taylor二阶展开),可将式(2)近似为
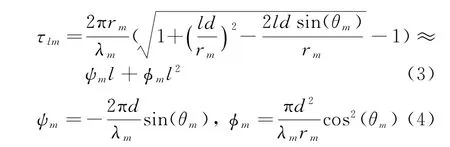
假定M个信源可分别表示为s1(t)ejω1t,s2(t)ejω2t,…,s M(t)ejωMt。 式(1)可用矩阵形式 表示为
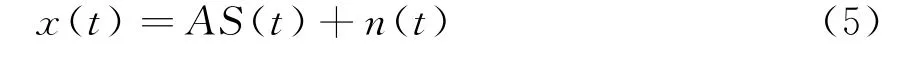
式中,
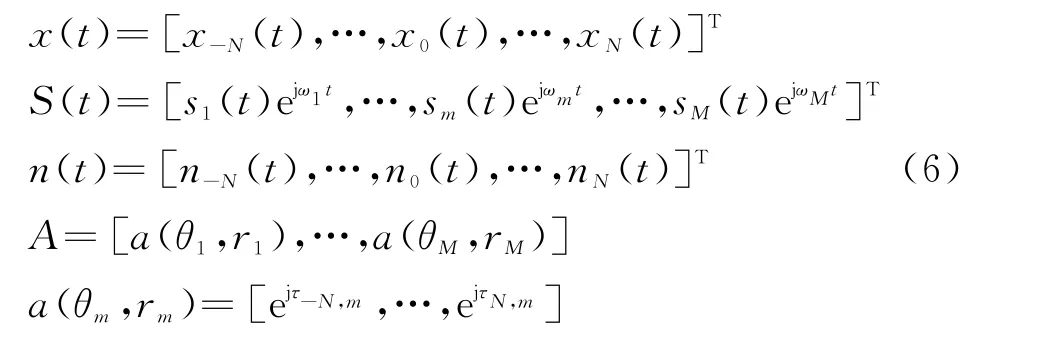
对信号模型作如下假设:
(1)源信号是相互统计独立并且具有非零峰度的非高斯过程。
(2)每个阵元上的加性噪声均是零均值的复高斯白噪声,且噪声与源信号以及各阵元噪声之间是不相关的。
(3)阵元间距d≤λm/2;线阵阵元个数N S满足N S>max[M,2]。
(4)基于具有2N+1个阵元的均匀对称线阵的情况下,与文献[7]中要求最大可容纳信源数M<N不同,本文只要求M<2N+1即可。
(5)每个源信号距离和波达角不完全相同。即(θi,r i)≠(θj,r j),对任意1≤i≠j≤M成立。
除上述假设外,源信号数目M的确定属于信号检测问题,已有文献详细研究该问题[15],因此,文中假设M是已知的。
2 三维参数的联合估计
矩阵A与远场情形一样称为近场信号的阵列流形矩阵,是DOA、距离以及频率的函数。S是以各个源信号经过采样得到的离散序列构成的行向量组成的矩阵,x是阵列接收数据矩阵。算法首先对白化后的阵列接收数据构造一组四阶累积量,再由联合对角化方法估计出阵列流形A和窄带信号源频率,最后根据阵列导向矢量a m和对应的源信号频率f m的结构特点,利用最小二乘估计出DOA和距离。
2.1 阵列流形A和信源频率的估计
(1)对混合观测数据x进行白化处理,构造白化矩阵Q使得QA为酉矩阵,R x表示阵列接收信号的协方差矩阵,由假设中噪声与信号不相关,协方差矩阵R x可表示为

对R x进行特征分解可得R x=VΣVH,其中Σ=diag(λ1,…,λM,σ2,…,σ2),且λ1≥…≥λM≥σ2=…=σ2,则根据文献[16]白化矩阵Q可以取为
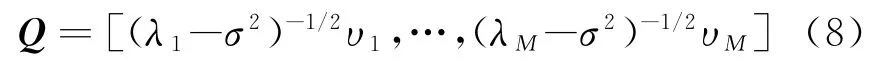
根据白化矩阵Q,进而得到白化数据(t)。
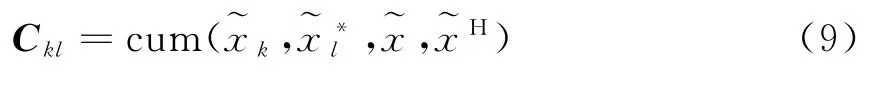
由上式,可以构造出M×(M+1)/2个四阶累积量矩阵C kl。
(3)令W=QA,白化后的接收数据,由高阶累积量的可加性以及高斯分布高阶累积量为零的性质,根据四阶累积量的定义,C kl可以写成如下形式:
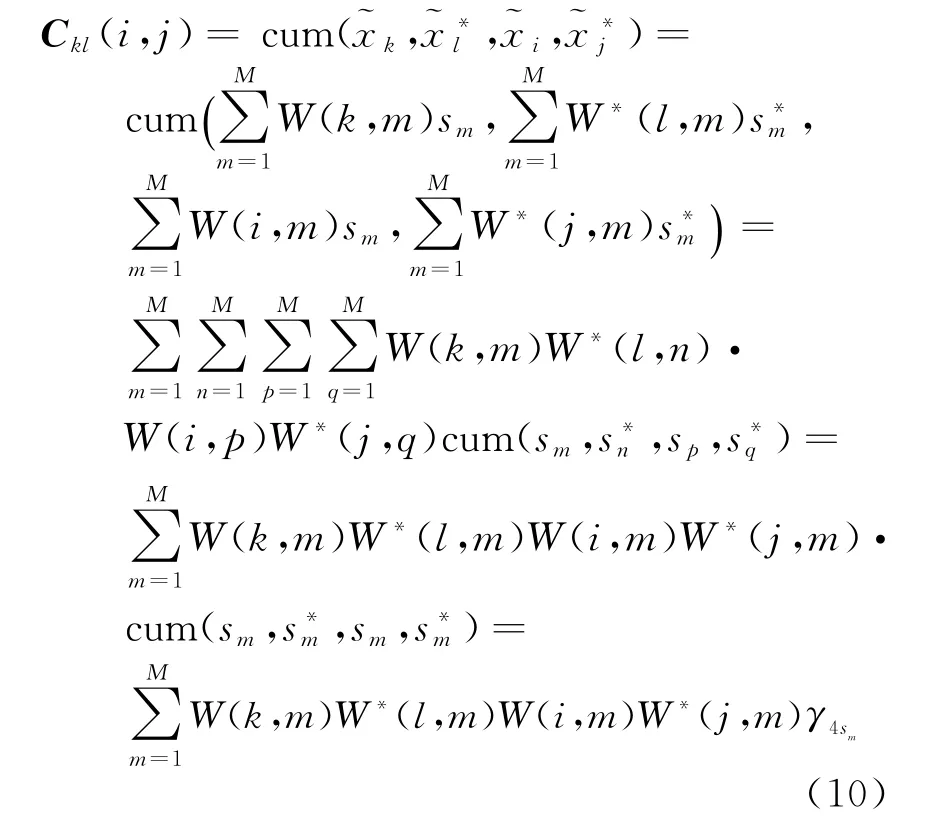
式中,W(i,k)表示矩阵W第i行第k列对应的元素;γ4sm为源信号s m对应的四阶累积量,且
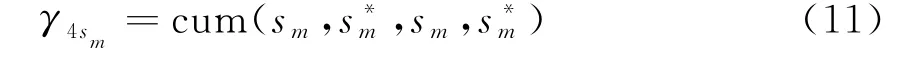
根据文献[15]可知存在一个酉矩阵W使得C kl可以被同时对角化,用矩阵形式具体可表示如下:

式中,对角矩阵Γkl=diag{W(k,l)W∗(l,1)γ4s1,…,W(k,M)W∗(l,M)γ4sM}。
(4)得到酉矩阵W,利用近似对角化方法,把所有M×(M+1)/2个矩阵{C kl}联合对角化,即可得到源信号的估计(t)WH以及混合矩阵的估计为,Q+为Q的伪逆。
由于联合近似对角化算法理论可知,≃AΛP,其中,Λ为一对角线元素非零的对角矩阵,P为一置换矩阵,它们分别对应于联合正交化算法的幅度和顺序不确定性,假设对角矩阵Λ=dia g{z1,…,z M},即令,则存在复常数z m(m=1,…,M),使得
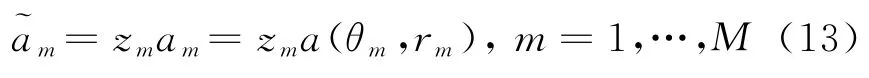
但是这并不影响由阵列导向矢量即阵列流形的列矢量来确定相应信号源的二维参数,并且对角化酉矩阵W与对角矩阵Γkl是在一次特征值分解中得到,因此源信号与得到的阵列流形是行列相互对应的,即每个信号源的采样离散序列在中的行位置与其对应的阵列导向矢量在中的列位置是顺序对应的。对估计出的源信号每一行进行频谱分析(文中采用离散傅里叶变换)得到M个信号源的频率{f1,…,f m,…,f M}。
2.2 距离和DOA的估计
利用已经估计出来的信源频率{f1,…,f m,…,f M},再用最小二乘方法得到阵列导向矢量中包含的距离和DOA参数,每个信源对应的频率、距离和DOA都估计出来以后,可以将频率、距离或DOA按升序或者降序排列,因此实际估计时可以忽略P带来的影响。
由式(3)、(4)和(6)可以看出,导向矢量a m的相位是阵元位置的二次函数,已假定对角矩阵则
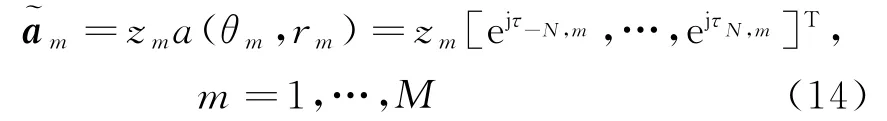
令

式中,~a m(i)表示~a m的第i个元素,所以c m是个2N×1维的矢量。
将式(9)代入式(10)可得
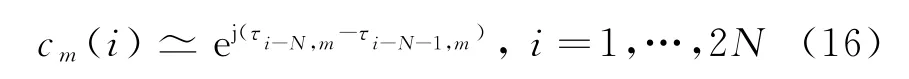
根据第m个源信号到阵元i-N和阵元i-N-1的距离r m,i-N和r m,i-N-1的距离差小于阵元间距(三角形两边之差小于第三边)可以得到|τi-N,m-τi-N-1,m|=2π|r i-N,m-r|/λm<2πd/λm,由假设可知d≤min(λm/2),1<m<M,所以|τi-N,m-τi-N-1,m|<π。
若用φm(i)表示c m(i)的相位,将式(4)代入上式可得
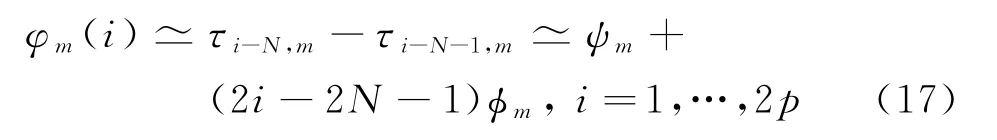
用矩阵可表示为

对上式利用线性最小二乘即可得到ψm,ϕm的估计。
近场源的到达方向和距离的估计公式如下:
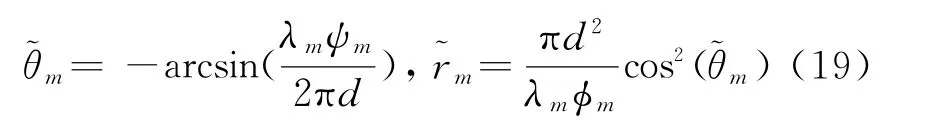
已知源信号频率,再结合对应的阵列导向矢量即矩阵的列向量可以得到对应信号源的到达角和距离参数。
3 仿真实验
假定源信号是两个等功率统计独立的空间信号可以分别表示为ej2πf1t+jα1和ej2πf2t+jα2,其中α1和α2均为[0,2π]上的均匀分布。入射到九元均匀线阵上,且阵元间距d=min(λ1,λ2)/4。试验中使用根均方误差(RMSE)作为性能评价标准:
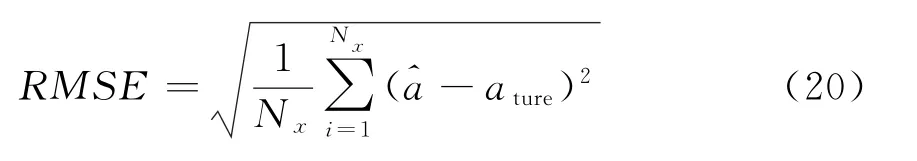
式中,为参数估计值,a为参数真值,N x为蒙特卡洛实验次数。
实验1 频率、DOA和距离分别为(3 M Hz,30°,2λ1)和(4 M Hz,20°,λ2),控制信噪比(SNR)从10 dB到20 d B,数据长度为4096个快拍。蒙特卡洛仿真次数为300次。两个信源频率、DOA及距离的估计结果如表1所示。
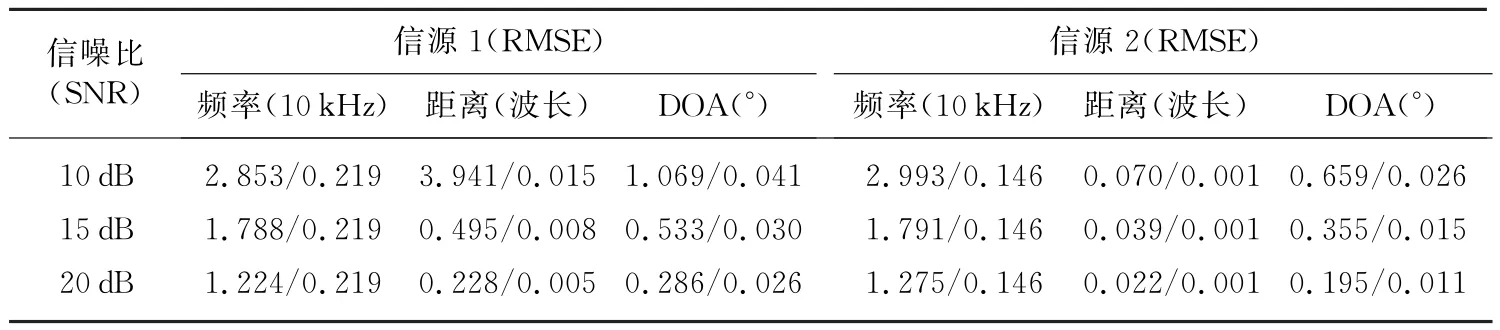
表1 不同信噪比下本文所提方法与基于高阶累积量的类ESPRIT方法的比较
表1中显示的是信源各个参数的均方根误差(RMSE),位于前面的数据是由基于高阶累积量的类ESPRIT方法所得,后面的数据则是本文所提算法所得。从仿真结果中可以看出在快拍数固定不变,随着信噪比的增加,各个参数估计的均方根误差呈减小趋势。而且从仿真结果中可以看出本文所提方法的估计效果明显比基于高阶累积量的类ESPRIT方法要好。
从图2可以看出,在信噪比小于-10 dB时,频率估计均方根误差明显减小;当信噪比大于-10 dB时,均方根误差变化不再明显,并逐渐趋于零。在SNR大于-10 dB时,频率估计精度已经较高且比较稳定。这恰好解释了表1中本文所提算法的频率估计RMSE基本不随信噪比变化的原因。
实验2 频率、DOA和距离仍分别为(3 MHz,30°,2λ1)和(4 MHz,20°,λ2),固定信噪比为15 dB,快拍数从500个变化到2 500个后,300次蒙特卡洛仿真后两个信源频率、DOA及距离三维参数的估计结果如表2所示。
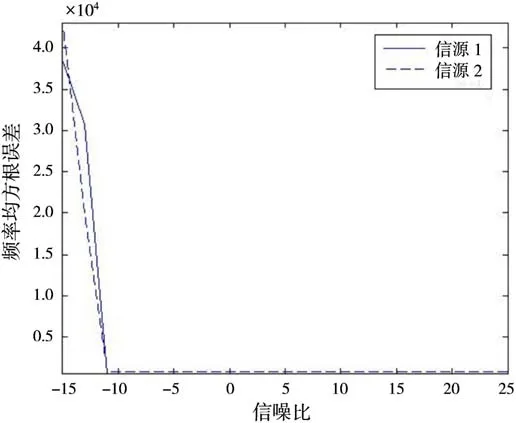
图2 本文所提方法下频率的估计结果
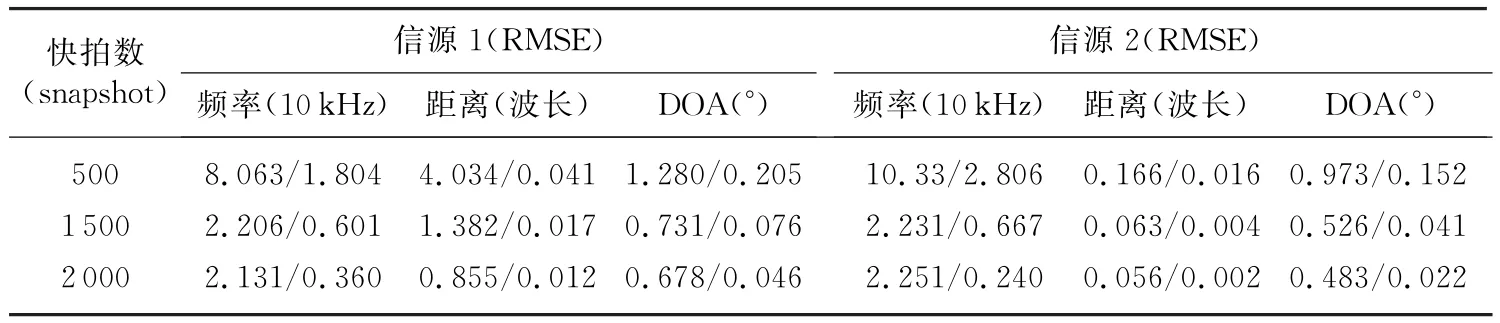
表2 不同快拍数下本文所提方法与基于高阶累积量的类ESPRIT方法的比较
从图3可以看出,频率的估计精度和采样点数成正比,采样点数越多,频率估计精度越好。这是因为频率是根据估计得到的源信号离散序列经过FFT提取频谱之后得到的,所以频率的估计精度和采样点数成正比。
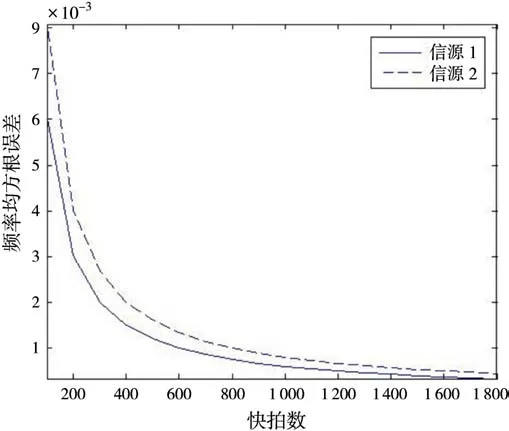
图3 频率估计随快拍数变化
表2中显示的是信源各个参数的估计均方根误差(RMSE),位于前面的数据是由基于高阶累积量的类ESPRIT方法所得,后面的数据则是本文所提算法所得。可以看出,频率、DOA和距离的估计精度随采样点数变化的趋势一致,都是随着采样数目的增大而变好,并且在信噪比相同的情况下,同样快拍数下本文所提算法表现更好。
实验3 为了直观表现本文方法的优越性,将本文方法与文献[17]中的基于高阶累积量的类ESPRIT方法进行比较,试验中信源为2个等功率的调幅信号,载波频率分别为f1=3 M Hz,f2=4 M Hz,带宽为25 k Hz,采样频率fs=12 MHz。两个信源的到达角分别为30°和20°,距离分别为2λ1和λ2。波速为光速,阵元间距为最小波长的0.25倍。信噪比固定为15 dB,快拍数固定为2 048,做300次Monte-Carlo实验,两个信号的频率、DOA和距离分布如图4和图5所示。
由上图中可以直观地看出,本文所提方法参数估计统计性能更好。
4 结束语
本文提出了一种基于高阶累积量矩阵的联合对角化的近场源频率、DOA和距离三维参数的联合估计方法。首先利用联合对角化方法得到高阶累积量矩阵的对角信息和对角化矩阵来估计阵列流形和各个源信号的离散序列构成的信号矩阵,对信号矩阵进行谱分析得到各独立信号源的频率,进而通过总体最小二乘方法估计出DOA和距离,所提算法在基于阵元数为2N+1的均匀对称线阵时可估计的最大信源数目为2N,与基于高阶累积量的类ESPRIT方法的仿真结果比较可以看出,本文所提方法在相同的信噪比和快拍数下表现更好,且从多次蒙特卡洛仿真的结果可以看出所提方法更稳健,并且参数自动配对,不需要搜索或者迭代等过程。
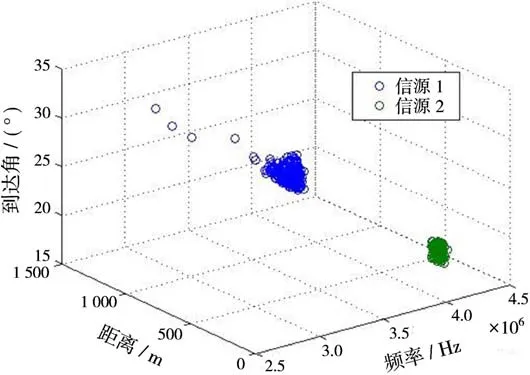
图4 基于四阶累积量的类ESPRIT方法
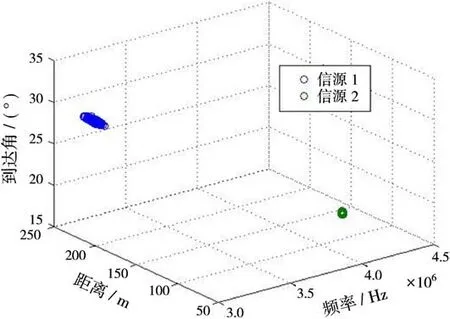
图5 本文所提方法
[1]Hoole P R P.Smart Antennas and Signal Processing for Communication,Biomedical and Radar Systems[M].Southampton:WIT Press,2001.
[2]郭艺夺,张永顺,童宁宁,等.基于L型MIMO雷达二维DOA估计新算法[J].雷达科学与技术,2010,8(5):412-416.GUO Yi-duo,ZHANG Yong-shun,TONG Ningning,et al.New Algorithm for 2-D DOA Estimation Based on L Shaped MIMO Radar[J].Radar Science and Technology,2010,8(5):412-416.(in Chinese)
[3]Swindlehurst A L,Kailath T.Passive Direction of Arrival and Range Estimation for Near-Field Sources[C]∥4th Annual ASSP Workshop on Spectrum Estimation and Modeling,Minneapolis,Minnesota,USA:[s.n.],1988:123-128.
[4]Huang Y D,Barkat M.Near-Field Multiple Sources Localization by Passive Sensor Array[J].IEEE Trans on Antennas and Propagation,1991,39(7):968-975.
[5]Russell J,Bell K L,Van Trees H L.Broadband Passive Range Estimation Using MUSIC[C]∥2002 IEEE International Conference on Acoustics,Speech,and Signal Processing,Orlando,Florida,USA:[s.n.],2002:2920-2922.
[6]Starer D,Nehoraj A.Path-Following Algorithm for Passive Localization of Near-Field Sources[C]∥5th Annual ASSP Workshop on Spectrum Estimation and Modeling,Rochester,NY,USA:[s.n.],1990:322-326.
[7]Challa R N,Shamsunder S.Higher-Order Subspace Based Algorithm for Passive Localization of Near-Field Sources[C]∥29th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA:[s.n.],1995:777-781.
[8]刁鸣,吴小强,李晓刚.基于四阶累积量的测向方法研究[J].系统工程与电子技术,2008,30(2):226-228.
[9]Grosicki E,Abed-Meraim K,Hua Y.A Weighted Linear Prediction Method for Near-Field Source Localization[J].IEEE Trans on Signal Processing,2005,53(10):3651-3660.
[10]陈建峰,张贤达,吴云韬.近场源距离、频率及到达角联合估计算法[J].电子学报,2004,32(5):803-806.
[11]黄家才,石要武,陶建武.近场源DOA、距离、极化参数及频率联合估计算法[J].计算机工程与应用,2006(19):17-19.
[12]Liang Junli,Zeng Xianju,Ji Bangjie.A Computationally Efficient Algorithm for Joint Range-DOAFrequency Estimation of Near-Field Sources[J].Digital Signal Processing,2009,19(4):596-611.
[13]周祎,冯大政,刘建强.基于联合对角化的近场源参数估计[J].电子与信息学报,2006,28(10):1766-1769.
[14]胡增辉,朱炬波,梁甸农.基于盲源分离的近场源参数估计[J].信号处理,2010,26(6):951-955.
[15]Shapo B,Bethel R.A Novel Passive Broadband Bayesian Detector/Tracker[C]∥Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop,Cambridge,MA,USA:[s.n.],2000:92-96.
[16]Belouchrani A,Abed-Meraim K,Cardoso J F,et al.A Blind Source Separation Technique Using Second-Order Statistics[J].IEEE Trans on Signal Processing,1997,45(2):434-444.
[17]吴建岚,胡光波,季锋.基于高阶累积量的近场源三维参数估计算法[J].舰船电子工程,2010,30(11):50-53.

