LDPC 码的级联译码算法的改进与实现

陈 猛

(中航雷达与电子设备研究院 1 部，江苏 无锡 214063)

LDPC(LDPC:Low Density Parity－Check)码是一类具有逼近香农限的译码性能纠错码，近年来受到了广泛的关注和研究。文献［1］中给出了LDPC 码在基于置信传播(Belief Propagation，BP)译码算法下的性能限，其推导建立在由Tanner 图中环所带来的错误传播可忽略的假设上，这就要求LDPC 码的码长达到一定长度。然而在实际应用中，由于对系统时延的要求，使得LDPC 码的码长不能过长，这就可能造成较大的译码性能损失。而级联译码算法被广泛应用于中短码长LDPC 码的译码中，已达到性能与复杂度的折中。

LDPC 码的级联译码是指将BP 译码所输出的软信息传送给基于可靠性的软判决译码器进行译码。文献［2］将排序统计译码(Ordered Statistic Decoding，OSD)算法嵌入BP 译码迭代之中，即在每次BP 迭代后均进行一次OSD 译码，从而有效提高了译码性能并减少了迭代的次数。更加实用的级联译码方案是指在最后一次迭代后进行可靠性译码，即将BP 译码与可靠性译码串行级联。文献［4］给出了一种串行级联译码方案，该方案通过对对数似然比进行累积(LLRA:Log－Likelihood Ratio Accumulation)以消除BP 算法输出软信息的震荡，从而改善送给可靠性译码的软信息的准确性。文献［5］对对数似然比累积算法进行了推广，得到了一种基于概率域的累积算法。

目前，多种最佳或次最佳的基于可靠性的译码算法被应用于LDPC 码的级联译码算法中，包括盒匹配(Box and Match Algorithm，BMA)算法［6］、缩减伴随式集译码(Reduced List Syndrome Decoding，RLSD)算法［7］、基于伴随式的OSD 算法［8］以及Chase－2 算法［9］等。文献［10］则将OSD 算法与一种基于最不可靠位置的最大似然译码算法并行执行。

到目前为止，大多数与级联译码相关的文献主要是对算法的研究与改进，而对于算法的实现，大多数文献仅给出了算法复杂度方面的分析，而并未给出具体的方案。多数基于可靠性译码算法在实现时的关键问题均在于其中高斯消元算法的实现。文献［10 ～11］分别给出了GF(2)和实数域上的高斯消元算法的硬件并行实现方案，然而这两种方案中均未考虑对待消元矩阵的存储所占用的资源优化，因此其在FPGA 实现时仅适用于规模较小的矩阵。对于码长达到几百甚至上千bit 的LDPC 码，使用文献［11］中的方案显然不可行。此外，考虑到高斯消元仅是整个译码器中的一部分，因此其实现方案需与BP 译码和OSD 译码的其他逻辑综合进行。

本文基于和积译码算法与OSD 算法的串行级联，给出了一种基于RAM 的FPGA 实现方案。

1 OSD 串行级联译码算法

OSD 串行级联译码算法的流程如图1 所示。首先对输入的软信息进行对数似然比累积的和积译码，然后判断译码校验和是否为零。若校验和为零，则直接输出和积译码的结果，即码字1。反之，则执行OSD 译码，并得到码字2 作为最终的译码输出。

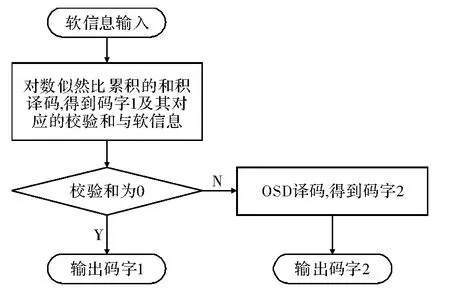
图1 具有门限的串行级联译码算法流程

对数似然比累积(Log－likelihood Accumulation，LA)算法通过将每次译码迭代所得到的软信息进行加权和以消除震荡，并将累积后的软信息记为，有

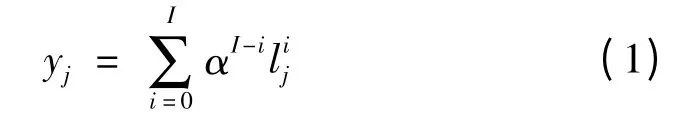
2 LDPC 码级联译码器的FPGA 实现

对于FPGA 实现，各种级联译码算法均需解决以下3 个主要问题:(1)如何实现对生成矩阵的存储。(2)如何高效地实现由输入软信息对生成矩阵的置换。(3)如何在有限的资源下实现维数高达数百的GF(2)上的高斯消元。

OSD 算法中需要存储LDPC 码的生成矩阵G，对于(n，k)LDPC 码，其生成矩阵为k×n 的矩阵。生成矩阵在FPGA 中的存储有两种方式:一种基于块RAM;另一种基于逻辑资源。文献［10 ～11］均是基于后一种方案，该方案可对每个bit 分别进行操作，具有灵活性高的优点，而前一种方案则只能对一行或一列统一操作。然而，对于码长在100 bit 以上的LDPC 码，采用后一种方案则并不划算，甚至在大多数中低端FPGA 中是不可能实现的。因此，实用的OSD 译码器中对G 的存储只能采用基于块RAM 的方案，此时就需要确定对G 的存储方式，即基于行进行存储或基于列进行存储。

构建MRB 时需根据可靠性度量r 的降序对生成矩阵G 的列进行排序，对于列排序，若将G 基于列进行存储，便可对每一列整体进行操作，从而降低排序运算的复杂度。OSD 译码中的GF(2)上高斯消元是由各种初等行变换操作实现的，因此若将矩阵G 按照行进行存储就可将每一行的操作并行进行，这样就可将高斯消元算法的时间复杂度降为O(k2)。

综上所述，OSD 算法在FPGA 实现时需解决的3个问题最终归可结为一个问题，即如何存储生成矩阵G。本文采用以下方案:

(1)对G 基于行进行存储以降低高斯消元的运算复杂度。

(2)对G 的列置换，通过操作和存储一个列映射函数来实现，其函数中存储的是置换后的列号。此时文中实际上并未对G 进行列置换，而只是对其列号进行了置换，这样便降低了列置换时的复杂度。

(3)为了简化行置换时对存储器的操作，对行置换也采用了与列置换类似的方法，即通过对行号的置换间接实现对G 的行置换，置换后的行号存储在行映射函数中。

图2 给出了一个采用上述基于行列映射函数对一个4×8 的矩阵从左至右进行高斯消元的结果，其中包含了对线性相关列的置换。

图2 基于行列置换函数的GF(2)上的高斯消元

最终，由上述方案，得到了如图3 所示的OSD 译码器。

图3 中，软信息分离模块实现对软信息的硬判决和求绝对值，得到硬判决码字cI和可靠性度量r。排序模块根据可靠性度量生成初步的列映射关系，只对列映射函数进行操作。高斯消元模块在排序之后对生成矩阵进行基于行列置换函数的高斯消元。码字置换模块根据列映射关系对硬判决的码字进行置换得到u。重编码模块基于行置换后的生成矩阵对u 进行编码得到候选码字cX。度量值计算模块对候选码字计算其译码度量值wX。最后由码字选择模块选择具有最小度量值的码字作为译码输出。

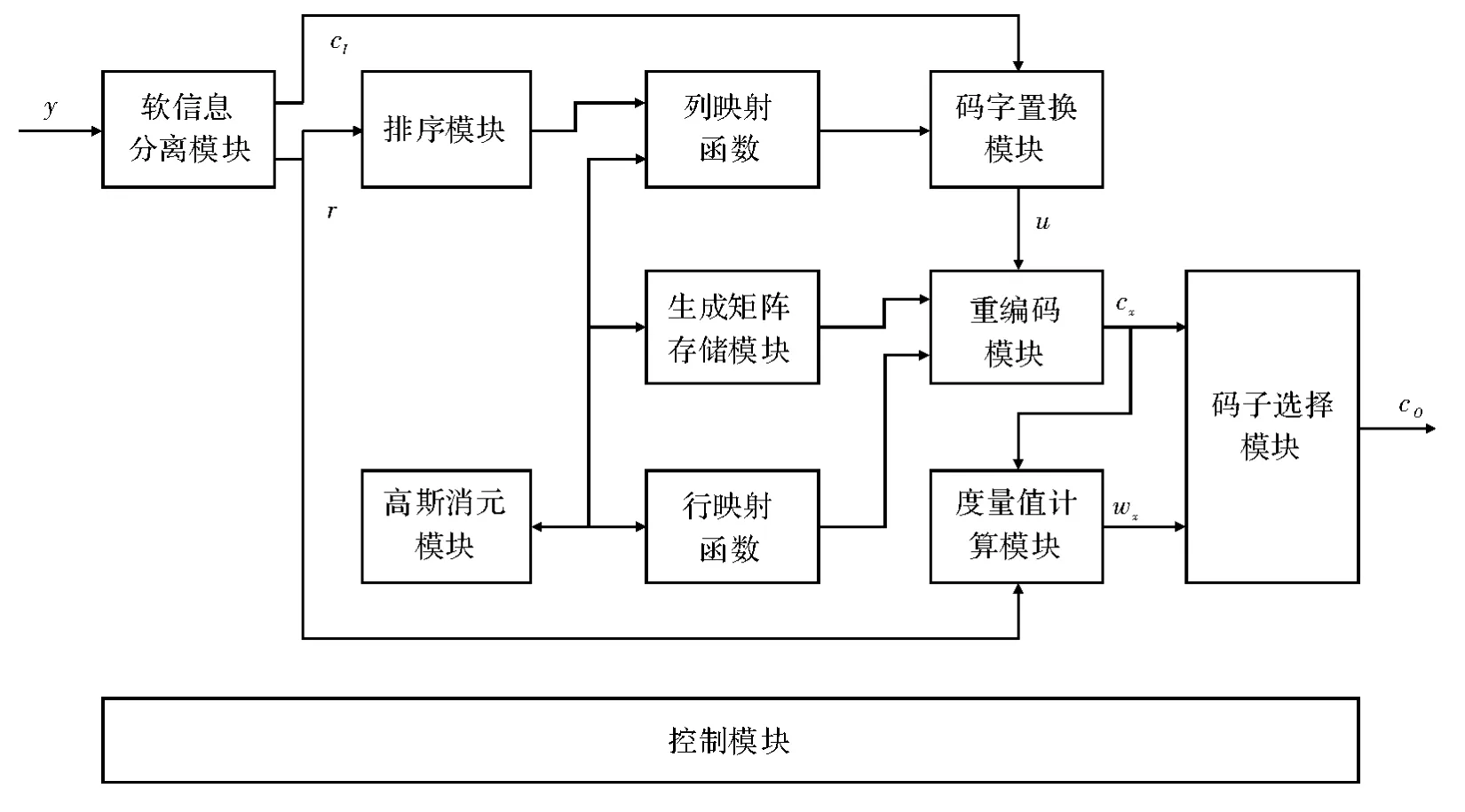
图3 OSD 译码器

上述方案中的重编码模块可利用LDPC 码的线性特性，对编码方案进行简化。若c=uG 为由生成矩阵G 定义的一个码字，其中u 为信息序列。对阶数为1的OSD 算法，需对u'=u+ei进行编码，其中ei表示第i 个位置为1，其他位置为0 的错误图样。编码过程可表示为

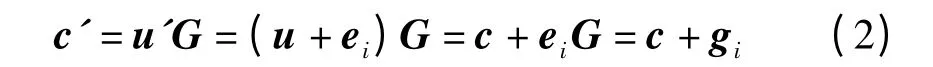
即重编码模块只需执行一次编码，对于不同错误图样，只需在第一次编码的结果上再加入生成矩阵的对应行即可。

3 实现结果

采用文献［13］中给出的一个码率R=1/3 的准循环(QC:Quasi－Cyclic)LDPC 码在FPGA 上实现了串行级联译码器。设定扩张因子z=24，对应的码长为576，使用的FPGA 为Altera 公司的EP3C80F484C8。其中OSD 译码部分的综合结果如表1 所示。

表1 综合结果

该OSD 译码器中各个模块所需的时钟数为:排序操作需消耗n 个时钟;高斯消元所需的时钟数与生成矩阵G 的前k 列中线性相关的列数有关，设线性相关的列数为x，则高斯消元所需的时钟数为k2+x。重编码操作消耗的时钟为2k，度量值计算操作以及最后的码字选择操作均只需1 个时钟。最终，OSD 译码器对一个接收码字进行译码所需的时钟约为k2+2k+n+x+2+p，其中p 为各级运算流水时延之和，其取值约为30。假设x=50，采用100 MHz 的时钟，则该OSD译码器的吞吐率为192×100 000/(1922+2×192+576+50+2+30)≈500 kbit·s－1。

4 结束语

本文针对基于FPGA 实现对中短码长LDPC 码的OSD 串行级联译码算法进行了优化，给出了一种基于行列映射的级联译码器实现方案。该方案使在具有时延要求的通信业务中，使用OSD 算法提高译码性能成为可能。另外，文中实现方案的核心是GF(2)上之中高斯消元算法的实现，因此该方案可应用于其他所有需要执行GF(2)上高斯消元的算法与系统之中。

［1］ RICHARDSON T J，URBANKE R L.The capacity of lowdensity parity－check codes under message－passing decoding［J］.IEEE Transactions on Information Theory，2001，47(2):599－618.

［2］ FOSSORIER M.Iterative reliability－based decoding of low－density parity check codes［J］.IEEE Journal on Selected Areas in Communications，2001，19(5):908－917.

［3］ GOUNAI S，OHTSUKI T.Lowering error floor of irregular LDPC codes by CRC and OSD algorithm［J］.Ieice Transactions on Communications，2006，E89B(1):1－10.

［4］ JIANG M，ZHAO C M，XU E Y，et al.Reliability－based iterative decoding of LDPC codes using likelihood accumulation［J］.IEEE Communications Letters，2007，11(8):677－679.

［5］ LI G W，FENG G Z.Generalised reliability－based syndrome decoding of LDPC codes［J］.European Transactions on Telecommunications，2008，19(8):873－877.

［6］ BIAN Y B，FENG G Z.A novel concatenation decoding algorithm for short LDPC codes with lower complexities［C］.Proceedings of 2009 Conference on Communication Faculty，2009:550－554.

［7］ 董自健，酆广增.一种基于缩减伴随式集的QC－LDPC 码级联译码算法［J］.电子与信息学报，2010，32(4):825－829.

［8］ 董自健，酆广增.基于伴随式的OSD 改进算法［J］.南京邮电大学学报:自然科学版，2011(1):35－38.

［9］ TONG S，ZHENG H J.On combining chase－2 and sumproduct algorithms for LDPC codes［J］.Etri Journal，2012，34(4):629－632.

［10］QIAO G L.Parallel decoding scheme based on OSD and KNIH algorithms［J］.Materials Science and Information Technology，2012(43):4813－4816.

［11］BOGDANOV A，MERTENS M C，PAAR C，et al.A parallel hardware architecture for fast gaussian elimination over GF(2)［C］.14th Annual IEEE Symposium on Field－Programmable Custom Computing Machines，Proceedings，2006:237－246.

［12］ZHANG B W，GU G C，SUN L，et al.Floating－point FPGA gaussian elimination in reconfigurable computing system［J］.Chinese Journal of Electronics，2011，20(1):51－54.

［13］ZTE，CATT，RITT，Huawei.R1－051070－comparison of structured LDPC codes and 3GPP turbo codes［S］.Sandiego USA:3GPP TSG RAN WG1#42bis，2005.