基于调度优先权的海上多物资应急调度方法

陈金晶

（浙江海洋学院海运与港航建筑工程学院，浙江舟山 316022）

基于调度优先权的海上多物资应急调度方法

陈金晶

（浙江海洋学院海运与港航建筑工程学院，浙江舟山 316022）

针对海上突发事件多物资应急调度存在优先权的问题，考虑到应急反应基地的运力无法满足将应急物资一次性运往事故点的要求，构建了有限运力下，满足各种应急物资应急限制期的前提下，使应急物资运输总时间最短的多物资调度模型，并给出了求解方法，最后通过算例仿真验证模型的有效性。

多物资调度；有限运力；调度优先权；多次运输

海上突发事件具有多物资需求特性，需要考虑物资的数量需求、质量需求和结构需求[1]。质量需求主要包括对物资重要性、时效性等方面的要求。不同的应急物资，对救援作业顺序，对事故救援所起的作用，对应急响应最长允许时间等方面的要求不同，因而在事故救援的过程中具有不同的调度优先权[2]。结构需求是指不同应急物资需求量之间的比例关系，通过数量需求和结构需求确定应急物资的总需求量。当所需调运的应急物资超过应急反应基地的运力，无法一次性将其物资全部运往事故点，而且应急物资调运又存在优先权时，要使应急救援工作及时有效地开展，必须在第一时间先将最紧要的物资送达事故点。因此，在运输能力相对紧张的情况下，应该根据应急物资的需求特性制定出相应的调度方法，保证应急物资在其各自的应急限制期内及时可靠地到达事故点。

目前，针对多物资应急调度的研究已有一定进展。戴更新等[3]根据多物资多出救点问题的特征，参考单种物资调度问题取得的成果，引入连续可行方案的概念，构建了多物资应急调度的数学模型。程序芳[4]在将物资需求分为重要需求和次要需求的基础上，设计了两次运输模式，建立以首次运输时间最小和两次运输总时间最小为目标的双目标运输分配模型，并应用多目标遗传算法设计算法求解。柴秀荣等[5]研究了多出救点多物资的应急调度问题，给出了在保证物资连续消耗，满足时间最短和出救点数目最少的调度算法，同时解决了物资储备中心到事故点的最短路径问题。高本河等[6]将n种物资的运输需求作为n个阶段，将m个应急中心提供的运输量作为决策标量，将应急中心的剩余运输能力作为状态变量，进而在上述转化下建立时间最短、出救点数目最少的模型，并给出贪心算法。但上述文献均认为，出救点到事故点的运输时间为一定值，没有考虑运输路网的不确定情况。其中文献[3,5]没有考虑应急物资具有调度优先权的问题。文献[4]未考虑出救点运力限制的问题。

笔者研究应急反应基地存在运力限制的条件下，考虑到海上运输的各种不确定性因素，将海上运输时间表示为区间数，然后根据应急物资的需求特性，确定各种应急物资的调度优先权，提出在满足各类物资的应急限制期的前提下，使应急物资调运时间最短的多物资调度方法。

1 问题描述

海上突发事件爆发后，受应急反应基地的物资储备量的限制，往往需要多个反应基地共同参与。同时，各个应急反应基地所有的救助船舶的载重能力也是有限的。当事故救援所需的物资种类和数量较多的情况下，救助船舶无法将应急物资一次性全部运往事故点，就需要考虑多次运输的问题。多次运输需要考虑往返运输时间。区别于陆上运输，海上救援环境复杂，受到风、浪、潮等气象水文条件的影响，救援船舶在反应基地和事故点之间的往返运输环境往往不同，应急物资的运输时间呈现很大的不确定性。因此，多次运输影响物资运输的总体可靠性和完成运输任务的时间。如何在应急反应基地运力受限的约束下，考虑海上事故类型对应急物资的不同需求特点，根据不同物资的调度优先权实现多物资的应急调度是本文研究的关键问题。

设A1，A2，…，An为n个应急反应基地，Ai表示第i个应急反应基地，i=1,2，……n。B为事故点，B共需要m（m>1）种应急物资。设X=(x1，x2……xm)，其中xj表示B对第j种物资的需求，j=1，2，……m，且假设各类物资的调度优先权的关系为w1＞＞w2＞＞…wm。Ai的第j种物资可用量为xij，i=1,2，……n，且满足从应急反应基地Ai调运到B的实际物资数量为设Ai的运输能力为Gi，i=1,2，……n，且至少存在某个i使第j种应急物资的应急限制期为TJ，Ai到事故点B的时间为事故点B到的时间为现需要给出一个调度方案，根据不同物资的调度优先权依次调运物资，要求满足各种物资的应急限制期，同时使物资调运时间最短，即确定参与的应急反应基地及相应的物资种类和数量。

2 运力限制下的多物资应急调度模型

2.1 模型构建

这里将m种物资的调运转化为m个阶段的决策过程[6]，每个阶段考虑一种物资的调运，优先权高的物资优先调运。如前所述，各类物资调度优先权的关系为w1＞＞w2＞＞…wm，所以，序号为1的应急物资优先调运，以此类推，直至事故点需要的各类物资调运完毕。每个阶段需要确定参与物资调运的Ai及其当然，为了提高救助船舶的装载率，节约调度成本，如果船舶装运一种物资后运力有剩余，可以装载后一种物资。

设 φ为任意选择的调运方案，φ=（φ1，φ2，…，φj，…，φm）。第 j个阶段对应的调运方案 φj，φj=其中第j种物资的应急限制期为Tj，T1＜T2＜…＜Tj＜…Tm。假定起始时间为调运完毕前j种物资的时间，考虑到应急物资调运时间具有连续性，因此完成第j种物资的调运时间为由此构建运力限制下的多物资应急调运模型：

式3.1：目标为应急物资调运时间最短；

式3.2：约束条件为分别满足每种应急物资的需求和时间限制要求。

本文假定应急反应基地的物资储备量满足事故点的物资需求，这里不需要考虑应急物资的集结时间及港口装卸时间，只考虑海上运输时间。由于海上运输的特殊性，受到事发时海上风、浪、潮等水文气象条件的影响，救援船舶的运输时间具有很大的不确定性，只能根据经验确定运输时间范围，即运输时间是一个区间数。通过区间数的相关理论可以将区间数映射到实数集上，从而将不确定问题转化为确定性问题来处理。本文采用文献[7]中的方法，通过定义加入决策者偏好参数的算子，把区间数序关系映射为实数序关系。设区间数A=[a,b]，w(A)=b-a为区间数A的区间宽度为区间中点，则通过定义一个算子λ，把区间数映射到实数集上[7]：

λ为决策者风险偏好算子，对于冒险型的决策者，取-0.5≤λ≤0；对于中立型决策者，取λ=0；对于保守型决策者，取0≤λ≤0.5。这样就可以用来比较不同区间数的序关系。

2.2 模型求解

记wij=min{wij，Gi}（j=1,2,…,m,i=1,2,……n），设nij为Ai的第j种物资可用量xij运送到事故点的往返次数，记Ai第一次将应急物资运往事故点的往返运输次数为零n），其中表示不大于的最大整数。设为Ai开始调运第j种应急物资时已经多次运输的次数。在实际的物资调运中，由于运输时间和运力的限制，反应基地Ai的物资可用量xij一般不可能全部运送到事故点B。设参与第j种物资调运的实际可能往返的次数范围那么Ai完成前j种物资调运的时间

设yj为事故点所需第j种物资是否完全调运的标志，为1表示已调运完毕。对于第j种物资来说，当承担最后一批物资运输的船舶运力有剩余时，可以顺带装运第j+1种物资，甚至第j+2,j+3…种物资。因此，设zj为承担第j种物资最后一批物资运输的救援船舶是否有剩余运力的标志，为1表示船舶有剩余运力。

步骤1：初始化，所有yj，zj初值置零。根据物资调度优先权排序，w1＞＞w2＞＞…wm，明确各种物资所处的调运阶段；

步骤3：根据每个反应基地Ai的xij和wij，算出nij，i=1,2,…,n。然后，对实际可能的运输时间从小到大排序，根据应急调运时间限制的要求，排除不满足时间限制期的运输时间。然后按照时间由小到大排序，依次选择反应基地调运物资量。若yj为1，计算出实际参与调度的反应基地的运输时间，并取其中最长的运输时间作为完成该物资调运的时间，然后转到步骤4；不为1，则继续调运物资，直至yj为1；

步骤4：判断zj的取值，若为1，则进入第j+1种物资的调运，然后判断yj+1的取值。若yj+1为1，则转到步骤4，继续判断zj+1的取值；若yj+1为0，则把第j+1种物资已经调运的数量从xj+1中扣除，然后转到步骤2；

步骤5：当所有yj(j=1,2……m)均为1，则调度完成，否则转到步骤2，继续调运。

本文根据上述求解思路，借助计算机编程，快速准确地得到模型的解。

3 算例分析

本文的仿真算例有5个备选应急反应基地，事故点共需要5种应急物资，且事先按照需求紧要程度对应急物资做了排序，即w1＞＞w2＞＞w3＞＞w4＞＞w5。表1为这5种物资的需求量、应急限制期、反应基地Ai到事故点B的往返运输时间范围物资可用量xij和运输能力Gi，这里λ取0.2。

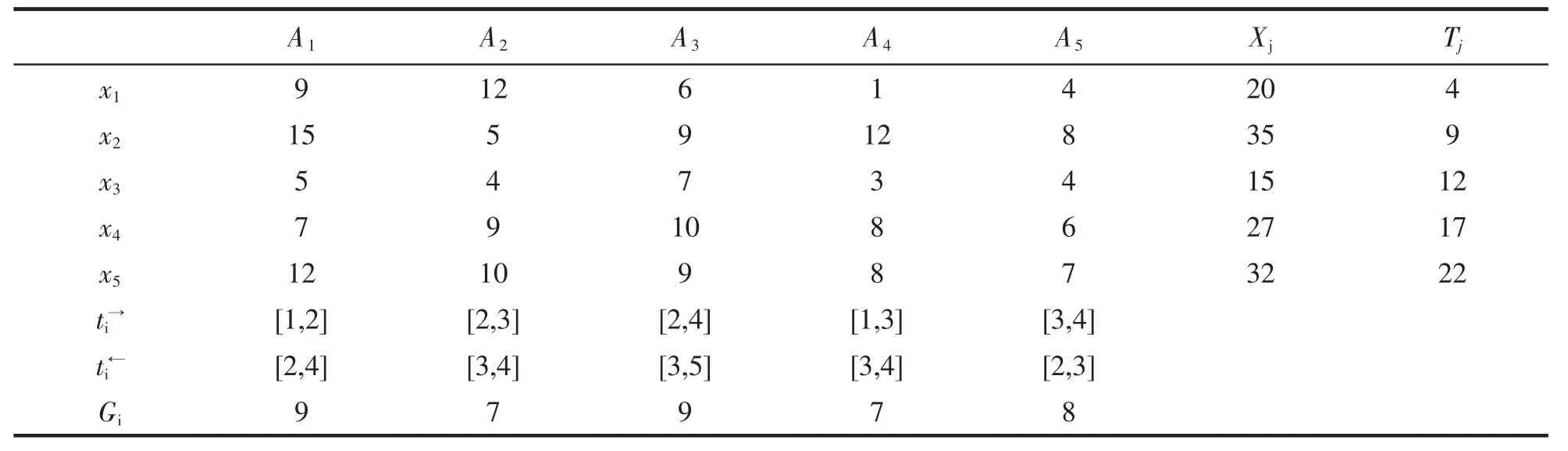
表1 算例数据Tab.1 Data of simulation example

将上述数据输入多物资应急调度程序中，得到如下结果，见表2。

表2 算例仿真结果Tab.2 Result of simulation example

由结果可知，物资1预计能在时间（2,4）内送达；物资2预计能在时间（5,10）内送达，其中通过反应基地A4顺带6个单位，A3顺带了6个单位；物资3预计能在时间（8,13）内送达，其中通过反应基地A4顺带1个单位；物资4预计能在时间（12,17）内送达，其中通过反应基地A2顺带3个单位，A5顺带了4个单位，A3顺带了3个单位；物资5预计能在时间（13,24）内送达，其中通过反应基地2个单位，A2顺带了4个单位。

此方案完成全部所需应急物资的时间范围为（13,24），且每种物资完成调运的时间都满足应急限制期。

4 结束语

本文以运力限制下的单物资应急调度的研究成果为基础，考虑到海上突发事件应急物资调度的实际情况，针对事故点需要调运的应急物资种类和数量较多，而应急反应基地运力受限的问题，遵循需求紧要的应急物资优先调运的原则，设计了在满足各种应急物资应急限制期的条件下使运输总时间最短的模型，并通过计算机编程求解，最后运用一个仿真算例验证了模型的有效性。但本文对海上来回程运输时间的不确定情况只是作了简单的处理，如何实现运输时间动态变化的应急物资调度是需要进一步讨论的问题。

[1]张 凡.考虑救灾物资需求等级的应急救援车辆调度[D].哈尔滨：哈尔滨工业大学,2007.

[2]王 军,陈金晶,陆永样.基于贪婪算法的水上应急物资调度优化方法[J].安全与环境学报,2013,13(5):254-258.

[3]戴更新,达庆利.多资源组合应急调度问题的研究[J].系统工程理论与实践,2000(9):P52-55.

[4]程序芳.基于需求分级的两次应急资源运输研究[J].哈尔滨商业大学学报:自然科学版,2010.27(1):121-124.

[5]柴秀荣,王儒敬.多出救点、多物资应急调度算法研究[J].计算机工程与应用,2010.46(6):224-226.

[6]高本河,伍慧飞.多资源调度中应急物流出救点最少问题的优化[J].物流技术2009,28(1):68-69.

[7]郭瑞鹏.物资调运时间为区间数的最短路问题研究[J].北京理工大学学报:社会科学版,2006.8(6):29-30.

[8]郑阿奇.C#教程[M].北京:BEIJINH电子工业出版社,2010.

Scheduling Model of Multiple Materials for Marine Casualties based on Priority of Scheduling

CHEN Jin-jing
（School of Shipping and Ports Architecture Engineering of Zhejiang Ocean University,Zhoushan 316022,China）

For there are priorities in the scheduling of multiple rescuing materials for marine casualties, taking into account that the transport capacity of the emergency response base cannot meet the demand of rescuing materials transported to where the accident occurred for one time,a scheduling model for multiple materials is established to minimize the transportation time on the basis of meeting the demand of the emergency response time.A simulation example is demonstrated to show how to apply this model.

scheduling of multiple materials;transport capacity;priority of scheduling;repeated transportation

TP301.6

A

1008－830X(2014)04－0377－05

2014-03-11

陈金晶（1987-），女，浙江舟山人，助理实验师，硕士，研究方向：应急管理、港航物流.Email:chenjinjingdlmu@126.com