油页岩原位加热电加热器温度分布模拟及优化设计

曾桂元王存新杨 浩

（1.中国石化西南石油工程有限公司钻井工程研究院，四川德阳 618000；2.中国地质大学，北京 100083）

油页岩原位加热电加热器温度分布模拟及优化设计

曾桂元1王存新1杨 浩2

（1.中国石化西南石油工程有限公司钻井工程研究院，四川德阳 618000；2.中国地质大学，北京 100083）

电加热是原位开采油页岩的方法之一，电加热器是其关键的加热元件。通过MATLAB的PDE工具模拟电加热器的温度分布，探讨了加热器导热系数、热源密度、密度、比热容、加热器尺寸等参数对加热效果的影响，以此作为电加热器优化设计的依据。研究指出，密度小的材料有利于提高加热器的加热效率；导热系数对温度影响不大；比热容越高，加热器的整体温度越低；随热源密度的增加，加热器的温度显著增加；正交实验分析指出，热源密度、密度、比热容对加热器温度分布影响较大，导热系数影响很小；加热器半径增加，温度增加。优化设计的加热器的形状为轴对称U型管和真空加热管，加热元件的材料为铜和不锈钢等。井下原位电加热不仅可以应用在油页岩的开采中，未来也可以作为稠油的开采技术。

油页岩；原位开采；电加热器；温度分布；数值模拟；优化设计

油页岩是一种含有固体可燃有机质的沉积岩，在所有的化石燃料中，若把储量折算为发热量，油页岩仅次于煤而列第二位，相当于目前世界探明原油可采储量的5倍多，是国际公认的传统石油资源的重要替代品之一［1-2］。

油页岩的常规开采方式［3］可分为露天开采和地下巷道开采两种。露天开采是露天剥土，直接采油页岩矿石，占用了大量土地，同时也对周围环境造成极大污染；地下巷道开采是在地下打巷道，用凿岩机采油页岩矿石，采出的油页岩矿石堆积在地面，同样占用了大量土地。而且这两种开采方式都需要把地下水位降低到含油页岩层的层位下，这样做会危害到矿山附近的耕地和森林。

地下热传导就地转化处理工艺技术［4-6］是在含油页岩地层中钻加热井，对油页岩层进行加热，稠油和气从干酪根中排出。根据加热源分为E-ICP（Electric Heating Technology of Insitu Conversion Process）工艺（电加热原位开采技术）和IVE（Technology-Insitu Vapor Exploring）工艺（原位热气（天然气、蒸汽）开采）。IVE工艺浪费大量宝贵的天然气资源，同时需要建设输气管道，成本高昂；如果注入热蒸汽，注入设备庞大，日常耗费高，设备占地面积大，经济效益差，更重要的是油页岩热裂解温度在350~560℃之间，注入的蒸汽考虑到热损失，无法达到该温度。而ICP工艺加热方式简单，施工方便，热效率高，占地面积小，加热器温度可以达到1 000 ℃以上，而且加热温度可以调控，因此电加热是油页岩开发的最优方法。但是，目前发表的文献［7-15］中未发现加热器研究的论文。本文以油页岩原位电加热器作为研究对象，模拟电加热器加热时的温度分布，研究加热器温度分布影响因素，优化设计加热器形状，优选加热器材料，为加热器优化设计提供参考。

1 电加热器温度分布模拟

1.1 电加热器物理模型

电加热井结构见图1a［16］。电加热器有限温部分，可以控制热量输出，以一种或多种加热速率来加热岩层。电加热井主要由以下部分组成：（1）引入线：主要用于进入电能，工作温度范围为40~90 ℃；（2）冷引线：用于充分降低导线加热器的温度；（3）接合部分：把冷引线连接到导线加热器，工作温度范围为260~370 ℃；（4）加热器：用于产生热量，温度在530~760 ℃；（5） 支撑部件：用于与导线加热器形成回路，避免短路；（6） 对中器（扶正块）：起扶正器作用，使支撑部件居中。为了数值模拟的方便，简化为图1b。

1.2 电加热器数学模型

考虑到井的轴对称性，电加热器考虑成单根圆柱体：内部均匀生热，上端绝热，底面和侧面与井底流体对流换热。热量均匀地产生，初始温度为相应深度的地层温度。为了充分体现加热器在径向和轴向的温度分布，采用柱坐标（r，θ，z），同时考虑到电加热器的轴向对称性，即与θ无关，因此可以用抛物型方程求解柱状物体的导热温度场，基本方程为：

图1 电加热井示意图

式中，u为温度，K；t为时间，s；ρ为密度，kg/m3；cp为比热容，J/（kg·K）；k为导热系数，W/（m·K）；qv为热源密度，kW/m3；r为径向半径，m；z为加热器长度，m。

边界条件：

式中，n为垂直于边界的单位矢量；h，r，q和g为常量或与u有关的变量。

方程（2）中的第1个方程称为狄利克雷（Dirichlet）边界条件，第2个方程称为纽曼（Neumann）边界条件。导热问题中的第一类边界与狄利克雷边界条件对应，第二类和第三类边界条件与纽曼边界条件对应。这些对应关系可以使用MATLAB中的PDE工具箱。

2 加热器温度场MATLAB数值模拟

2.1 假设条件

（1）电加热器位于井中心；

（2）井周物性条件一致；

（3）电加热器热物性参数恒定，不随温度变化。

2.2 计算参数

利用MATLAB的PDE Toolbox GUI 模拟图1b中加热器的温度分布。加热器为一裸电极金属杆，具体长度根据井下需要加热的油页岩层厚度及井下温度分布的数值模拟确定。密度ρ取7 800 kg/m3，比热容cp取500 J/（kg·℃），导热系数k取40 W/（m·℃），热源密度qv取750 kW/m3，加热器侧表面和底面与水的对流换热系数λ为50 W/（m2·℃），上端绝热，加热器长度z取1 m。

图2、图3是模拟的加热器温度分布云图，可以看出，由于上部绝热，温度比较高；下部及侧面由于热对流，温度稍有降低；由于加热器的轴对称性，温度也对称分布。可见，数值模拟真实地反映了电加热器的温度分布特性。

图2 10 000 s时二维温度场

图3 10 000 s时三维温度场视图

3 电加热器优化设计

3.1 电加热器影响因素研究

使用MATLAB对加热器进行温度场模拟时，加热器本身的参数包括：导热系数、热源密度、密度、比热容、加热器尺寸等。分析这些参数的变化对加热器温度场分布的影响，为优化设计加热器提供参考。采用2.2节计算参数，把密度、导热系数、比热容、热源密度、加热器半径分别作为单一变量，导出模拟数据，读出10 000 s时加热器的温度值。Ta是最高温度与最低温度平均值，Td是最高温度与最低温度差值。

3.1.1 密度 从表1可看出，密度越低加热器的整体温度越高，即密度小的材料有利于提高加热器的加热效率，但是密度小的材料不利于温度的均衡分布。

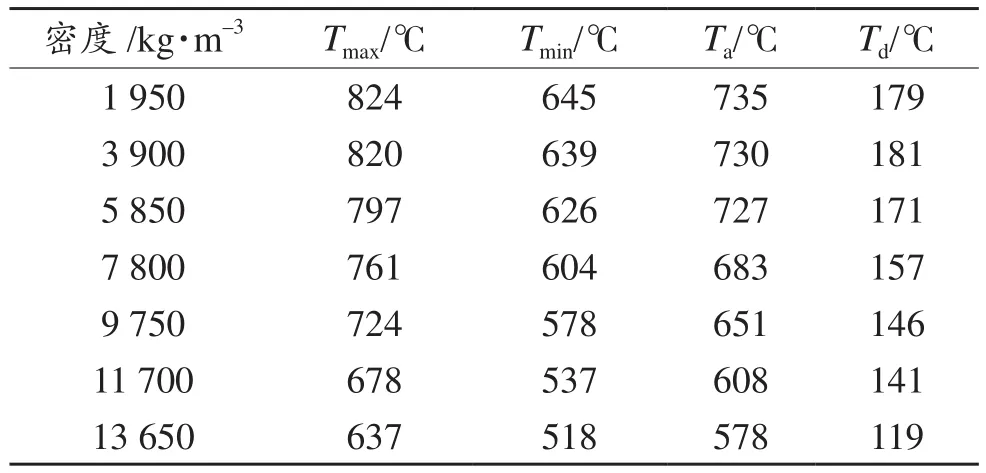
表1 不同密度下温度分布

3.1.2 导热系数 从表2可看出，导热系数越高，温度变化越小，但导热系数高有利于加热器温度的均衡分布。

表2 不同导热系数下温度分布

3.1.3 比热容 从表3可看出，材料的比热容越高，加热器的整体温度越低，但比热容高有利于加热器温度的均衡分布。

表3 不同比热容下温度分布

3.1.4 热源密度 从表4可看出，随热源密度的增加，加热器的温度显著增加。这是因为热源密度是功率与体积的比值，热源密度增加意味着功率的增加，所以温度会显著上升，但同时也引起加热器温度分布不均衡增加。热源密度的大小可以作为加热器设计的参考。

表4 不同热源密度下温度分布

3.2 物性参数影响分析

利用正交实验方法分析物性参数对温度分布的影响。通过对加热器温度分布的模型推导及数值模拟，确定了对加热器温度分布有明显影响的4个因素（表5）：密度（因素A）、导热系数（因素B）、比热容（因素C）和热源密度（因素D）。以加热器的最高温度作为考察指标，对加热器温度分布进行了4个因素3个水平L9（34）正交试验，结果见表6。

表5 因素和水平

表6 正交试验结果统计

根据极差Rj的数据可知，极差：D＞A＞C＞B，即当因素D、A、C水平变动时，指标波动较大，其中因素D指标波动最大，因素B指标波动最小。因此在设计加热器时要重点考虑调整热源密度、密度、比热容。

3.3 加热器的形状优化设计

3.3.1 理论分析 在电压一定的条件下，研究加热器尺寸对温度分布的影响。根据功率和电阻率公式导出加热器热源密度qv和热流密度qA

式中，e为电阻率，Ω·m；U为电压，V；z为加热器长度，m；r为加热器半径，m。

可以看出，随着加热器半径的增加，热流密度增加；热源密度大小与加热器长度有关。

3.3.2 数值模拟 参数设置同2.2，模拟不同半径加热器下的温度分布，结果见表7， 可以看出，数值模拟结果与理论分析吻合：加热器半径增加，热流密度增加，温度增加；加热器由于体积增大，不同位置温差也增加。

表7 不同半径下温度分布

3.3.3 形状优化设计 根据理论分析，在加热器材料和外载电压相同的情况下，热源密度是加热器长度平方的倒数，即降低加热器的长度有利于提高加热器的温度，因此最小的长度是需要加热的油页岩层的长度；同时考虑到形成回路，可以采用U型管，再根据井的对称性，因此考虑相互垂直的U型管。又根据加热器半径越大，温度越高，同时考虑到“趋肤效应”，可以把加热器中心部分除去，同时可以节约材料；加热器通过底部接触器与加热器中心部分形成回路，中心部分连接电缆；为了保护电缆在高温下正常工作，回路和加热器的环空抽成真空，隔绝加热器的高温。设计的加热器示意图见图4。加热器可以和注入管柱、抽油泵等配合，在加热的同时注入和抽出井底流体。

图4 加热管结构示意图

3.4 加热材料的优选

选取铁、铜、铝、不锈钢、镍铬合金、钨、石墨，进行加热器材料的优选。材料参数见表8。

表8 各种材料特性参数

分别选取半径0.1 m、长度1 m的圆柱形铁、铜、铝、不锈钢、镍铬合金、钨、石墨作为加热器的发热元件。其侧表面和底面与表面流体的对流换热系数λ均为50 W/（m2·℃）。设铁的热源密度qv=750 kW/ m3为相对值1，根据式（3）计算出对应的热源密度。初始温度设为35 ℃。各材料的传热系数、比热容、密度从表8中读取。分别模拟10 000 s时的温度分布情况，结果见表9。

表9 各种材料的相对热源密度和模拟结果

由于油页岩的集中热解温度为350~560 ℃，加热元件的温度一般控制在760 ℃左右，过高会使加热井附近产生过热现象，导致油页岩提前发生炭化结焦现象，损坏井眼内部设备。

模拟结果显示铜、铝的温度最高。铝的熔点在660 ℃，不符合要求。纯铜的熔点1 083 ℃，非纯铜的熔点低于这个值；铜的电阻率很小，即相对于其他材料，加热元件会做的较细，结构强度相对较低；另外，铜价格较高，也不符合要求。

钨金属是常用的灯丝材料，白炽灯灯丝的温度超过2 000 ℃，钨是熔点最高的金属，达3 410 ℃，导热性和导电性良好。模拟结果也显示钨材料的加热器表现十分优异，温度分布较均匀，整体温度相对较高。但是钨灯丝用来发光都是在隔绝氧气的情况下，原因是钨在高温时性质不稳定，易于与其他多种物质发生化学反应。然而原位开采油页岩的周期3~5年以上，其所需的加热器必须满足耐久性，钨金属的高温不稳定性是其致命的缺点。此外，钨在以上六种金属中价格最高。所以，钨不适合作为井下加热器的发热元件。

石墨材料的模拟温度最低，是上述材料中惟一的非金属材料，然而石墨具有很多类金属性质，比如良好传热、导电能力。此外，石墨的的熔点很高，在3 000 ℃以上，性质稳定。1 200 ℃以下其电阻温度系数为负值为另一个显著特点，说明温度越高电阻率反而越小。石墨的密度约为钢铁的1/4，即便是电热器制作较粗的情况下，仍具有体积价格（单位体积的价格）优势。但是由于其电阻率较高，发热功率低；此外，与金属材料相比，石墨的强度与机械性能较差，很难满足井下的施工要求。

镍铬合金耐蚀性强，高温强度高，成型加工和焊接性能好。缺点是价格高，并且不宜在含硫环境中使用。温度场模拟与表9可以看出相对于铁和不锈钢，镍铬合金的温度分布较低。作为一种常用的电阻丝，镍铬合金电阻率较高，即功率相同时所需的电压较高。

铁的各项物性参数略优于不锈钢，温度高于不锈钢，较不锈钢价格上也要低。但不锈钢在高温下（1 200 ℃）仍有较好的机械性能，高温蠕变性和电阻温度系数较低。最重要的是不锈钢在耐腐蚀性、高强度、硬度较高、焊接性能优越等方面明显优于金属铁。

壳牌公司E-ICP工程的加热材料为1Cr13不锈钢和铜，具有较高的居里温度，有耐高温硫化和耐低电偶腐蚀及较高蠕变温度的性能［16］；德国斯尼文特公司（Schniewindt）采用铜作为法兰加热器的加热材料；王爱民［17］采用电缆铜导线产生热量。可见，铜和不锈钢是主要的加热元件。镍铬等合金通过调整性能，也能作为加热器元件使用。

综上，铜、不锈钢、镍铬合金可以作为井下加热器的加热材料。

4 结论

（1）通过MATLAB的PDE方程得出了井下电加热器的温度分布及密度、导热系数、比热容、热源密度、加热器半径等物性参数对温度分布的影响：密度小的材料有利于提高加热器的加热效率；导热系数对温度影响不大；比热容越高，加热器的整体温度越低；热源密度增加，加热器温度显著增加；热源密度、密度、比热容对加热器温度分布影响较大，导热系数的影响很小；加热器半径增加，温度增加。优选了加热元件材料为铜、不锈钢和镍铬合金。优化的加热器形状为轴对称U型管和真空加热管。

（2）井下原位电加热不仅可以应用在油页岩的开采中，未来也可以作为稠油的开采技术。

［1］刘招君，董清水，叶松青，等.中国油页岩资源现状［J］.吉林大学学报：地球科学版，2006，36（6）：870-876.

［2］李术元，马跃，钱家麟.世界油页岩研究开发利用现状——并记2011年国内外三次油页岩会议［J］.中外能源，2012，17（2）：8-14.

［3］刘德勋，王红岩，郑德温，等.世界油页岩原位开采技术进展［J］.天然气工业，2009，29（5）：128-132.

［4］康志勤.油页岩热解特性及原位注热开采油气的模拟研究［D］.太原：太原理工大学，2008.

［5］汪友平，王益维，孟祥龙，等.美国油页岩原位开采技术与启示［J］.石油钻采工艺，2013，35（6）：55-59.

［6］汪友平，王益维，孟祥龙，等.流体加热方式原位开采油页岩新思路［J］.石油钻采工艺，2014,36（4）：71-74.

［7］RANGEL-GERMAN E R,SCHEMBRE J,SANDBERG C,et al.Electrical-heating-assisted recovery for heavy oil［J］.Journal of Petroleum Science and Engineering,2004,45（3-4）:213-231.

［8］ESPINOSA-PAREDES G,GARCIA-GUTIERREZ A.Estimation of static formation temperatures in geothermal wells［J］.Energy Conversion and Management,2003,44（8）:1343-1355.

［9］ESPINOSA-PAREDES G,MORALES-DÍAZ A,OLEAGONZÁLEZ U,et al.Application of a proportionalintegral control for the estimation of static formation temperatures in oil wells［J］.Marine and Petroleum Geology,2009,26（2）:259-268.

［10］ESPINOSA-PAREDES G,ESPINOSA-MARTÍNEZ E G.A feedback-based inverse heat transfer method to estimate unperturbed temperatures in wellbores ［J］.Energy Conversion and Management,2009,50（1）:140-148.

［11］AOUIZERATE G,DURLOFSKY L J,SAMIER P.New models for heater wells in subsurface simulations,with application to the in situ upgrading of oil shale［J］.Computational Geosciences,2012,16（2）,519-533.

［12］BURNHAM A K,DAY R L,HARDY M P,et al.AMSO's novel approach to in-situ oil shale recovery［C］.Oil Shale:A Solution To The Liquid Fuel Dilemma,ACS Symposium Series 1032,American Chemical Society 2010.

［13］RODRIGUEZ R F,BASHBUSH J L,RINCON A C.Feasibility of using electrical downhole heaters in Faja heavy oil reservoirs［R］.SPE 117682,2008.

［14］GASBARRI S,DIAZ A,GUZMAN M.Evaluation of electric heating on recovery factors in extra heavy oil reservoirs［R］.SPE 149779,2011.

［15］McQUEEN G,PARMAN D,WILLIAMS H.Enhanced oil recovery of shallow wells with heavy oil:a case study in electro thermal heating of california oil wells［C］.56th Annual Petroleum and Chemical Industry Conference,Anaheim,2009.

［16］王盛鹏，刘德勋，王红岩，等.原位开采油页岩电加热技术现状及发展方向［J］.天然气工业，2011，31（2）：114-118.

［17］方朝合，郑德温，葛稚新.壳牌ICP技术现场试验［J］.科技创新导报，2010（36）：110-111.

［18］王爱民，王志明.电加热空心抽油杆驱动螺杆泵装置［J］.石油机械，1998，26（3）：36-38.

（修改稿收到日期 2014-08-17）

〔编辑 朱 伟〕

Simulation and design optimization of temperature distribution of in-situ heating electric heater for oil shale

ZENG Guiyuan1,WANG Cunxin1,YANG Hao2
（1.Research Institute of Drilling Engineering,SINOPEC Southwest Petroleum Engineering Co.,Ltd.,Deyang618000,China;2.China University of Geosciences,Beijing100083,China）

Electric heating is one of the ways to in-situ retorting oil shale,and electric heater is the key heating component.Through simulating temperature distribution of electric heater by PDE tool in MATLAB,this paper discusses the effect of heat conductivity coefficient of the heater,heat source density,density,specific heat capacity,heater size,etc.on heater effectiveness and uses these parameters as the basis for design optimization of electric heaters.The research findings show that the materials with low density is helpful in improving heating efficiency of the heater;the heat conductivity coefficient poses small effect on the temperature;the higher the specific heat capacity is,the lower the overall temperature of the heater is;with the increase of heat source density,the temperature of the heater is increased remarkably.Orthogonal experiment shows that heat source density,density and specific heat capacity have great effect on heater temperature distribution,while heat conductivity coefficient has little effect;with the increase of heater radius,the temperature increases accordingly.The heater of design optimization takes the shape of U-tube and vacuum heating tube with axial symmetry,and the materials of heating components are copper and stainless steel,etc.Downhole in-situ electric heating can not only be used for development of oil shale,but be used as a technique for developing heavy oil.

oil shale;in-situ retorting;electric heater;temperature distribution;numerical simulation;design optimization

曾桂元，王存新，杨浩.油页岩原位加热电加热器温度分布模拟及优化设计［J］.石油钻采工艺，2014，36（5）：84-89.

TE357

：A

1000–7393（2014） 05–0084–06

10.13639/j.odpt.2014.05.020

国家潜在油气资源（油页岩勘探开发利用）产学研用合作创新研究项目（编号：OSR-04-07）。

曾桂元，1965年生。2004年毕业于中国石油大学（华东）油气田开发专业，获工学硕士学位，主要从事钻井现场作业管理和相关理论研究工作，高级工程师。电话：0838-2300316。E-mail： jameszeng65@163.com。