连续油管管内摩擦压降计算模型与敏感性分析

陈 勋闫 铁毕雪亮栾石柱李 洋杜婕妤

（1.东北石油大学石油工程学院，黑龙江大庆 163318；2大庆油田采油五厂，黑龙江大庆 163453；3.华北油田公司采油工程研究院，河北任丘 062552）

连续油管管内摩擦压降计算模型与敏感性分析

陈 勋1闫 铁1毕雪亮1栾石柱1李 洋2杜婕妤3

（1.东北石油大学石油工程学院，黑龙江大庆 163318；2大庆油田采油五厂，黑龙江大庆 163453；3.华北油田公司采油工程研究院，河北任丘 062552）

连续油管压裂作业过程中，压裂液除了在连续油管井下直管段流动，同时也会流入缠绕在滚筒上的那部分连续管，螺旋段的流动非常复杂，现有模型的计算结果与工程实际有一定的差距，基于流体力学基本原理，结合直管段摩擦因数公式和螺旋段几何特征，给出了连续油管螺旋段摩擦因数的一般关系式，最后经理论推导建立了完整的连续油管压裂作业管内压降的计算模型。分析了连续油管管径、滚筒直径、排量、黏度和流性指数等参数对管内压降的影响规律。结果表明：该模型的计算结果精度较高；相同条件下，螺旋段的压降总是大于直管段的压降；连续油管管径对压降的影响最大，管径增大近1倍，压降却减小了13倍，而滚筒直径对压降的影响最小，选择不同的滚筒直径，压降几乎未发生变化。

连续油管；摩擦压降；计算模型；螺旋段；敏感性分析

连续油管压裂作业时间不及常规作业时间的一半，尤其是在多层压裂和漏、掉产层的压裂中，连续油管压裂的费用仅为常规压裂的60%~70%。该技术已经在国外成功应用［1］，在国内特别是低渗油藏应用潜力巨大［2］。与常规压裂作业不同的是，压裂液必须流入缠绕在滚筒上的连续管中［3］，由于二次流现象的影响，这一部分油管内流体的摩擦压力损失较大，同时其流动也较复杂，作为整个油管压力损失的一部分，正确估算缠绕在滚筒上的连续管内的压力损失是很重要的。

国外学者Srinivasan［4］、White［5］、Ahmed［6］、Ogugbue等［7-10］对不同流体（清水、聚合物、表面活性剂等）在连续油管中的流动进行了大量的物理实验，并从实验结果回归推导摩擦因数计算公式，但是这些公式的计算结果与工程实际还存在一定的差距；国内学者张晋凯［11］、张小宁等［12-13］通过对连续油管进行数值模拟，研究流体在螺旋管中的流动规律以及压降变化规律，但是没有提出确切的计算公式。因此在前人的研究基础上，结合流体力学基本原理和连续管几何特征，通过理论推导，建立了连续油管压力损失的计算模型，并利用管径、滚筒直径、排量和流体特性等参数计算了螺旋段和直管段的压降，为连续油管压裂技术现场配套设备和施工参数的选择提供了理论基础。

1 压降模型的建立

连续油管压裂作业过程中压裂液在管内流动时压力损耗主要分为螺旋段压降和直管段压降2个部分（见图1）。这2部分流道形状差异较大，应采取分段单独计算的方法来计算压降，求解步骤为：（1）根据压裂液的流体特征，判断流体属于牛顿流体还是非牛顿流体（幂律流体）；（2）根据密度、流量或流速、管内径、流体特征参数（黏度、流性指数、稠度系数）等基本参数，求出管内压裂液的雷诺数，并判断流态（层流、紊流）；（3）选取相应的数学模型求出水力摩擦因数；（4）最后根据圆管压降计算方程求出两段压降。

图1 连续油管压裂作业示意图

根据连续油管压裂作业的特点，在实际工程计算中，做以下假设：（1）压裂液在整个管路的流动均为等温流动；（2）压裂液为不可压缩流体；（3）压裂液的流体特征参数在整个管路中的变化可以忽略。

1.1 雷诺数的计算及流态判别

对于牛顿流体，雷诺数的计算公式

式中，Re为雷诺数，无因次；ρ为流体密度，kg/m3；v为流速，m/s；di为连续油管内径，m；μ为黏度，Pa·s。

当Re＜2 100时为层流，反之则为紊流。

对于幂律非牛顿流体，可根据式（2）求出管内流体的雷诺数

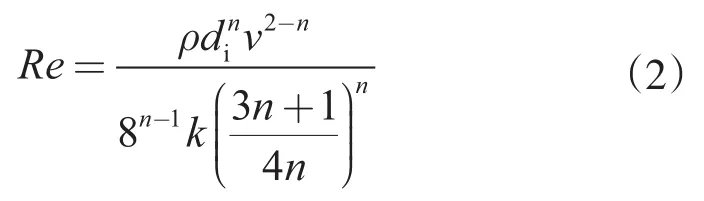
式中，k为稠度系数，Pa·sn；n为流性指数，无因次。连续油管直管段判断流态临界雷诺数为

连续油管螺旋段判断流态临界雷诺数为

其中参数C1和C2确定方法见公式（5）、（6）

若Re＜Rec则为层流，反之则为紊流。

1.2 摩擦因数的确定

1.2.1 直管段 无论连续管内流动的是牛顿流体还是非牛顿流体，其摩擦因数可以用下面的关系式［14］进行求解，即

式中，f为摩擦因数，无因次；a和b为计算参数，且层流和紊流时a、b值不同。对于层流，a=16，b=1；对于紊流，a、b的值由流性指数 （牛顿流体n=1）确定，具体见公式（8）、（9）

1.2.2 螺旋段 Srinivasan、White等人针对几种特定的流体在连续油管内的摩擦压降进行实验，由此得到的理论公式预测结果与工程实际差距较大，在现场应用中就不太适用了。因此，借鉴直管段的摩擦因数计算公式，假设螺旋段摩擦因数与计算参数a、b、雷诺数有关，此外由于连续油管还缠绕在滚筒上，所以螺旋段摩擦因数还与滚筒直径和连续油管直径有关，则螺旋段摩擦因数f与参数a、b、Re、di、D一般关系式为

通过实测获得螺旋段压降（见表1），据此对式（11）的系数（A1、A2、A3、A4、A5）进行回归得到非牛顿流体在连续油管螺旋段紊流流动摩擦因数

牛顿流体在连续油管螺旋段中处于紊流时的摩擦因数的计算公式为

层流时采用Srinivasan建议的公式计算摩擦因数，此公式适用于牛顿和非牛顿流体

1.3 压降计算

由流体力学基本原理可知，圆管内压降计算方程为

式中，Δp为压降，Pa；L为管长，m。

流量Q=vπdi2/4，如果以流量Q代替速度v，则式（15）可转化为

式中，Q为体积流量，m3/s。

把式（7）、式（12）、式（13）和式（14）分别代入式（16）中，可推导出连续油管各部分的压降计算公式。

（1）螺旋段压降。

牛顿流体紊流流动

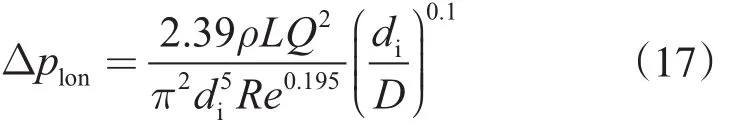
非牛顿流体紊流流动

牛顿流体、非牛顿流体层流流动

（2）直管段压降。

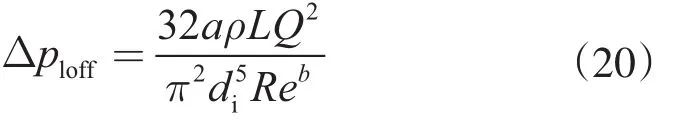
流体在连续油管内总的压降应为螺旋段和直管段两部分之和。

2 压降算例及敏感性分析

2.1 实例计算

基本参数：滚筒直径为2 080 mm，连续油管外径为63 mm，连续油管壁厚为4.44 mm，连续油管总长为3 500 m；压裂液密度为1.2 g/cm3，流性指数为0.6，稠度系数为6×10–5Pa·sn。结果如表1所示。

表1 连续油管压降测试试验数据与计算数据

2.2 敏感性分析

假设连续油管总长3 200 m，为了便于对比，又假设螺旋段和直管段长度一致，都为1 600 m，滚筒直径为1 778 mm，连续油管外径为60.3 mm，壁厚4.44 mm，排量1.2 m3/min，压裂液密度1.3 g/cm3，流性指数0.5，稠度系数0.001 Pa·sn。

2.2.1 连续油管管径 在不改变其他条件的情况下，根据《连续油管技术手册》［15］选取不同管径的连续油管，对总压降，螺旋段压降和直管段压降进行计算比较，对比结果如图2所示。对于同一管径，螺旋段压降总是大于直管段压降，如Ø31.75 mm螺旋段压降为111.7 MPa，直管段压降为53.7 MPa。由于离心力的作用，在螺旋管内流动时流体在垂直轴向方向沿管截面产生了二次流，使压降增大。对于不同直径的连续油管，小管径的压降明显大于大管径的压降，Ø31.75 mm的连续油管总压降为165.4 MPa，而Ø60.3 mm的连续油管总压降大幅降低到11.6 MPa，随着管径的增大，总压降、螺旋段压降和直管段压降都减小了，起初压降显著减小，然后逐渐趋于平缓，这是因为管径增大，雷诺数减小，摩擦因数变小，摩擦压降也随之减小。连续油管管径只增大了近1倍，但是压降却减小了13倍，因此在现场应用时，建议选用大管径的连续油管作为施工管柱。

2.2.2 滚筒直径 在不改变其他参数的情况下，根据《连续油管技术手册》选取不同滚筒直径（1 524 mm、1 778 mm、2 083 mm）的连续油管，对总压降进行计算比较，对比结果如图3所示。相同条件下，滚筒直径增大，总压降、螺旋段压降、直管段压降都减小，但是减小的程度不明显，例如滚筒直径为2 083 mm时总压降11.4 MPa，滚筒直径为1 524 mm时总压降11.7 MPa。因此，滚筒直径对连续油管总压降的影响很小，现场应用时几乎可以不考虑。

图2 连续油管压降随管径变化规律

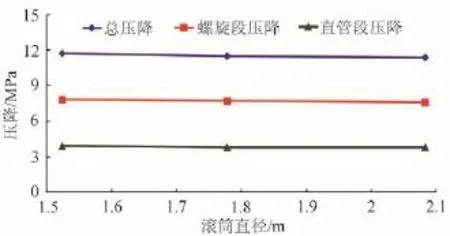
图3 连续油管总压降随滚筒直径变化规律

2.2.3 排量 在不改变其他参数的情况下，选择排量的变化范围为0~3 m3/min，连续油管总压降、螺旋段压降和直管段压降对比结果如图4所示。随着排量的增大，总压降、螺旋段压降和直管段压降都增大，流量为1 m3/min时总压降为8.6 MPa，当流量增加了1倍达到2 m3/min时，总压降增加了2倍升高至26.4 MPa。这是因为排量增大，雷诺数Re增大，摩擦压降也随之增大。

图4 连续油管压降随排量变化规律

2.2.4 黏度 假设压裂液流变特性与牛顿流体类似时，黏度是牛顿流体的重要流体参数，考察不同黏度下压降的变化规律，结果如图5。随着黏度的减小，总压降、螺旋段压降和直管段压降都逐渐减小。这主要是因为压裂液在连续管内流动多为紊流，流体质点的运动随机变化，形成大小不等的旋涡；黏度降低后，大尺度旋涡可以从流体中吸收能量发生变形、破碎进而向小尺度旋涡转化。小尺度旋涡在黏滞力作用下被减弱、平息，其所携带的部分能量转化为热能而耗散。在近管壁的边界层内，由于管壁剪切应力和黏滞力的作用，这种转化更为明显。

图5 连续油管压降随黏度变化规律

2.2.5 流性指数 假设使用的压裂液流变特性与幂律流体接近，则流性指数n是一个重要的流体参数，不同n下压降变化规律见图6，由图可知，在其他条件不变的情况下，n值越大，压降越大，例如当n=0.8时，总压降为30.6 MPa，当n=0.4时，总压降减小到7.6 MPa，即n减小1倍时总压降减小了3倍多。这是由于n值越大，流体表观黏度随剪切速率增加而降低的幅度不断减小，导致压降减小。

图6 连续油管压降随流性指数变化规律

3 结论

（1）基于流体力学基本原理，结合直管段摩擦因数公式和螺旋段几何特征，给出了连续油管螺旋段摩擦因数的一般关系式，最后经理论推导建立了完整的连续油管压裂作业管内压降的计算模型。

（2）相同条件下，由于二次流的影响，螺旋段的压降总是大于直管段的压降。

（3）对影响连续油管摩擦压降的因素进行了分析，压降与连续油管管径和滚筒直径成反比，与排量、黏度、流性指数成正比变化，影响连续油管压降因素的敏感性由大到小为连续油管管径、流性指数、排量、黏度、滚筒直径。

（4）现场应用中可通过选用大尺寸连续油管、减小排量的方法降低连续油管压降。

［1］CONNELL M L,HOWARD R G.Coiled-tubing fracturing operations ［J］.Offshore,2003,63（4）： 70-72.

［2］王海涛，李相方.连续油管技术在井下作业中的应用现状及思考［J］.石油钻采工艺，2008，30（6）：120-123.

［3］林英松，蒋金宝，刘兆年.连续油管压裂新技术［J］.断块油气田，2008，15（2）：118-121.

［4］SRINIVASAN P S,NANDAPURKAR S S,HOLLAND F A.Friction factors for coils ［J］.Transactions of the Institution of Chemical Engineers,1970,48： 156-161.

［5］VASHISTH S,NIGAM K D P.Experimental investigation of pressure drop during two-phase flow in a coiled flow inverter ［J］.Industrial and Engineering Chemistry Research,2007,46（16）： 5043-5050.

［6］AHMED H,AHMED K.Friction pressure losses of fluids flowing in circular conduits［C］.Offshore Technology Conference,Houston,Texas,USA,2012-4-30.

［7］OGUGBUE C C.Laminar and turbulent friction factors for annular flow of drag-reducing polymer solutions in coiled-tubing operations［J］.SPE Drilling &Completion,2011,26（4）： 506-518.

［8］BHARATH N R.Friction pressures of newtonian and nonnewtonian fluids in straight and reeled coiled tubing ［R］.SPE74847,2002.

［9］ZHOU Y,SHAH S N.New friction-factor correlations for non-newtonian fluid flow in coiled tubing ［J］.SPE Drilling &Completion,2006,21（1）： 68-76.

［10］WILLINGHAM J D,SHAH S N.Friction pressures of newtonian and non-newtonian fluids in straight and reeled coiled tubing ［R］.SPE 60719,2000.

［11］张晋凯，李根生，黄中伟，等.连续油管螺旋段摩阻压耗数值模拟［J］.中国石油大学学报：自然科学版，2012，36（2）：115-119.

［12］张小宁，姜凤光，李根生，等.泡沫在连续管螺旋管段内流动的压降数值模拟［J］.石油钻采工艺，2011，33（6）：5-9.

［13］蔡子龙.连续油管钻井内部流动分析［D］.湖北荆州：长江大学，2012.

［14］GALLEGO F,SHAH S N.Friction pressure correlations for turbulent flow of drag reducing polymer solutions in straight and coiled tubing ［J］.Journal of Petroleum Science and Engineering,2009,65（3-4）：147-161.

［15］李宗田.连续油管技术手册［M］.北京：石油工业出版社，2003：109-120.

（修改稿收到日期 2014-08-20）

〔编辑 薛改珍〕

Calculation model for internal frictional pressure drop in coiled tubing and analysis of sensitivity

CHEN Xun1,YAN Tie1,BI Xueliang1,LUAN Shizhu1,LI Yang2,DU Jieyu3
（1.Petroleum Engineering College,Northeast Petroleum University,Daqing163318,China; 2.No.5Oil Production Plant,Daqing Oilfield Limited
Company,Daqing163453,China; 3.Petroleum Production Engineering Research Institute,Huabei Oilfield Company,Renqiu062552,China）

Unlike the conventional fracturing operation,the fracturing fluid not only flows in straight section of downhole coiled tubing,but also flows into the part of coiled tubing which is wound on the reel.The flow in spiral section is very complex,and the calculation results from existing model is somewhat different from the actual engineering practice,so a general relation was given to the friction factor in the spiral section of the coiled tubing based on principle of flow mechanics and in combination with friction factor equation of the straight section and the geometric characteristics of the spiral section;finally a complete calculation model for internal pressure drop during fracturing operation in coiled tubing was built with theoretical derivation.Analysis was conducted of the effect law of parameters like coiled tubing diameter,drum diameter,displacement,viscosity and flow index on internal pressure drop.The result shows that the accuracy of the calculations by this model is high;under the same conditions,the pressure drop in spiral section is always greater than that in straight section;the diameter of coiled tubing poses the greatest impact on pressure drop;when the diameter is increased by 1 time,the pressure drop reduces by 13 times,while the drum’s diameter has the smallest impact on pressure drop,so no matter what size of the drum is,the pressure drop almost remains the same.

coiled tubing;frictional pressure drop;calculation model;spiral section;sensitivity analysis

陈勋，闫铁，毕雪亮，等.连续油管管内摩擦压降计算模型与敏感性分析［J］.石油钻采工艺，2014，36（5）：13-17.

TE22

：A

1000–7393（2014） 05–0013–05

10.13639/j.odpt.2014.05.004

国家自然科学基金资助项目“基于热质流耦合的深层欠平衡钻井井筒温度场和压力场分布规律研究”（编号：51374077）。

陈勋，1984年生。2012年获东北石油大学油气井工程硕士学位，现为博士研究生，主要从事油气井工艺与流体力学方面的研究工作。电话：0459-6500886。E-mail：chenxunsun@126.com。