定向钻井PDC钻头切削参数计算方法

邹德永王家骏于金平郭玉龙赵 健卢 威

（1.中国石油大学（华东）石油工程学院， 山东青岛 266580；2.华北油田公司，河北任丘 062552）

定向钻井PDC钻头切削参数计算方法

邹德永1王家骏1于金平1郭玉龙1赵 健1卢 威2

（1.中国石油大学（华东）石油工程学院， 山东青岛 266580；2.华北油田公司，河北任丘 062552）

定向钻井PDC钻头的优化设计和导向性能分析需要准确计算PDC切削齿的切削面积、切削体积和切削弧弧长等切削参数。针对弯外壳螺杆马达或推靠式旋转导向系统，运用空间解析几何理论和数值计算方法，分析了PDC钻头在井底的运动状态，建立了切削齿的运动轨迹方程和切痕曲线方程。综合考虑了钻头偏转角、钻头的复杂运动、钻头结构参数及切削齿切削的先后次序等因素的影响，建立了切削齿的切削面积、切削体积和切削弧弧长等切削参数的数值计算方法，为PDC钻头的计算机优化设计和定向钻井PDC钻头的导向性能分析提供了一种分析手段。实例计算表明，模型和方法具有实用性，可进一步推广应用。

PDC钻头；切削齿；切削参数；运动轨迹；定向钻井

在定向钻井PDC钻头的优化设计和导向性能分析中，需要准确计算出每个切削参数。文献［1］假设钻头轴线始终与井眼轴线重合，并且沿着井眼轴线（铅垂线）方向运动，建立了垂直钻井时PDC钻头的切削参数计算方法。而在定向钻井过程中，钻头轴线与初始井眼轴线之间有钻头偏转角，并且钻头在钻压和侧向力作用下有沿着井眼轴线向前运动和垂直于井眼轴线的侧向运动，因此直井中的切削参数计算方法并不适用于定向井。笔者在综合考虑了钻头偏转角、钻头的复杂运动、钻头结构参数及切削齿切削的先后次序等因素的基础上，运用空间解析几何理论和数值计算方法，建立了PDC切削齿的运动轨迹方程和切痕曲线方程，给出了切削参数的数值计算方法。

1 钻头在井底的运动状态分析

定向钻井时，使用的钻具通常有：单弯外壳螺杆马达双稳定器钻具组合（见图1a）和推靠式旋转导向系统（见图1b）。用纵横弯曲梁法对上述2种钻具组合受力分析，求出钻头上的钻压W、侧向力Fl和钻头偏转角λ（侧向力Fl是变井斜力Fα和变方位力FΦ的合力，λ可以分解为变井斜平面内的偏转角λ1和变方位平面内的偏转角λ2），分析钻头在钻进前后与井眼的几何关系。在图1中，初始时钻具组合用蓝色线画出，钻进后的钻具组合用红线画出。设钻头在钻压W和侧向力Fl作用下分别向下钻进了ha，向侧向钻进了hl。

图1 底部钻具组合的简化模型

当使用弯外壳螺杆马达滑动导向钻井时，初始时钻头轴线O3X3与井眼轴线O2X2之间的夹角为钻头偏转角λ。设近钻头扶正器与井壁接触点从A点到B点是一段圆弧，其曲率半径为R，则钻进后的钻头轴线O4H与初始钻头轴线O3X3夹角为δ。δ可以分解为变井斜平面内的偏转角δ1和变方位平面内的偏转角δ2。

当使用推靠式旋转导向系统导向钻井时，初始时钻头轴线O3X3与井眼轴线O3X3之间的夹角为钻头偏转角λ。钻进过程中钻头轴线O4H与初始时钻头轴线O3X3平行。

由于使用不同种类的钻具，钻头在井底的运动不同，所以需要针对这2种情况分别建立的切削齿运动轨迹方程。

2 PDC切削齿的运动轨迹方程

设某钻头共有N个切削齿，其切削齿号码记为i∈（1，N）。如图2所示，建立6套坐标系来描述切削齿与钻头和井眼的坐标关系。

图2 PDC钻头的复合坐标系统

（1）直角坐标系O1-X1Y1Z1为大地坐标系。

（2）直角坐标系O2-X2Y2Z2为初始井眼坐标系。原点O2为初始井底中心，Z2轴为井眼轨迹在O2的切线方向。平面O2-X2Y2为变井斜平面，平面O2-Y2Z2为变方位平面。

（3）直角坐标系O3-X3Y3Z3为当前井眼坐标系。在定向钻进过程中，原点O3随着钻头中心一起移动，Z3轴与钻头轴线O4H始终重合，而X3和Y3轴不随钻头旋转而改变方向。当使用弯外壳螺杆马达滑动导向钻井时，初始时，Z3轴与Z2轴的夹角为钻头偏转角λ，钻进过程中Z3轴与Z2轴的夹角为 。当使用推靠式旋转导向系统导向钻井时，初始时钻头轴线O3X3与Z2轴的夹角为λ+δ，钻进过程中Z3轴与Z2轴的夹角始终为λ。

（4）圆柱坐标系O4-RHθ为钻头坐标系。原点O4为钻头中心，初始时与原点O2重合，钻进过程中与原点O3重合。H轴为钻头轴线，始终与Z3轴重合。R轴与钻头基准线夹角为周向角θ，设钻头在X2、Y2、Z2方向上每转进尺分别为hx、hy、hz，钻头基准线与X3轴的夹角为钻头旋转角ω。初始时钻头基准线与X2轴重合，钻进中的t时刻的钻头旋转角为ωt。此刻原点O4在O2坐标系中的坐标为（x0，y0，z0）

（5）平面直角坐标系O5-X5Y5为切削齿工作面坐标系。该坐标系在切削齿切削面上，原点O5为切削齿中心。令第i号切削齿的半径为ri，将切削齿工作面边缘称为切削刃，设切削刃上任意一点P的坐标为（xc，yc）

（6）平面直角坐标系O5-X6Y6为切削齿剖面坐标系。过第i号切削齿中心O5和钻头轴线建立切削齿的剖面。X6轴与X5轴夹角为切削齿的侧转角βi，Y6轴与Y6轴夹角为切削齿的后倾角αi，Y6轴与Z3轴的夹角为切削齿的法向角γi。设点P在O5-X6Y6中的坐标为（xd，yd）

由式（1）~式（4）可得，使用螺杆马达滑动导向钻井时，切削刃上任意一点P的运动轨迹方程

由式（2）~式（4）可得，使用推靠式旋转导向系统时，切削刃上任意一点P的运动轨迹方程

当R=Ri，H=Hi时，为第i号切削齿中心的运动轨迹方程。

3 PDC切削齿的切痕曲线方程

在初始井眼坐标系O2-X2Y2Z2中，当t=t1时刻，钻头基准线与X3轴夹角为ω1，将第i号切削齿中心坐标（Ri、Hi、Qi、）代入式（5、6）中得该齿中心为Xg1，Yg

1，Zg

1，将此时刻的第i号切削齿剖面O5-X5Y5称为Ⅰ平面（下文简称为Ⅰ平面）。在初始井眼坐标系中Ⅰ平面的方程为

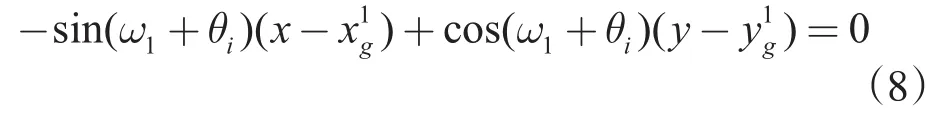
将第i号齿和其邻齿的齿中心坐标代入式（5）或式（6）中，可得切削刃上任意一点P的运动轨迹方程。用迭代法求点P的运动轨迹到Ⅰ平面的距离为0的数值解，即与Ⅰ平面的交点，将交点连成线就是切削刃的切痕曲线。使用最小二乘法，将切痕曲线拟合成非标准椭圆方程，方程形式为

式中，a、b、c、d、e、f为系数，称式（9）为切削齿的切痕曲线方程。

4 切削参数计算

当钻头中心O4在初始井底O2时，各切削齿在Ⅰ平面上的切痕曲线称为该齿的初始切痕曲线。当钻头中心O4在当前井底O3时，各切削齿在Ⅰ平面上的切痕曲线称为该齿的当前切痕曲线。第i号切削齿的切削面积是初始切痕曲线与当前切痕曲线所围成图形的面积。设在某布齿密度下，第i号切削齿的切削面积只与左边2个邻齿和右边两个邻齿有关。

如图3，红色区域为第i号切削齿的切削面积，其不仅与该切削齿的尺寸、吃入深度、位置及空间方向有关，还取决于相邻切削齿的重叠切削作用。采用数值积分的方法求各个切削齿的切削面积。

第i号切削齿切痕曲线在X6轴上覆盖的范围为（ni，mi），切削面积的计算方法如下。

（1）将（ni，mi）划分为j个等长的小区间，取每个小区间的中点坐标 作为计算点，小区间的宽度为w。

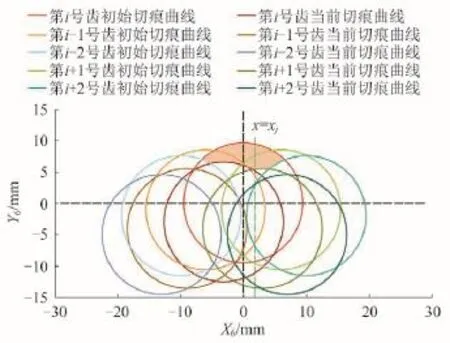
图3 切削齿初始切痕曲线和当前切痕曲线

（2）按式（9）计算每个小区间内与中点坐标xj对应的有效y坐标。当且仅当xj∈（ni，mi）时，直线x=xj必然与该切痕曲线相交于上、下2个交点，由于切削齿的切削面积总是位于Ⅰ平面坐标系O5-X6Y6的Y6轴正半轴，所以y值取正值。将射线x=x与各齿初始切痕曲线的交点记为yd（xj），将射线x=xj与各齿当前切痕曲线的交点记为yu（xj），比较这些值的大小和各切削齿的切削次序，得到最大值，则有

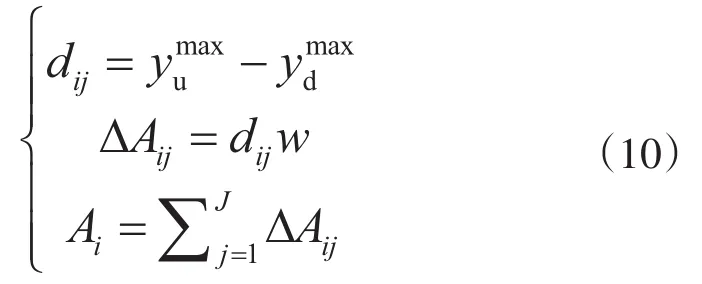
其中第i号切削齿的第j个小区间的切削深度为dij，小区间的面积为ΔAij，第i号切削齿的切削面积为Ai。接触弧长的计算方法同文献［1］。

根据文献［2］中的PDC切削齿力学模型，输入切削参数、岩石可钻性和后倾角求出小区间的正压力Fn

j和切削力Fcj。所有小区间的合力是整个切削齿的正压力Fn和切削力F。根据文献［2］中钻头合力计算方法，由各切削齿的受力和布齿参数可以求出钻头的钻压和侧向力。这就建立了钻头钻速与受力之间的关系模型。

计算流程首先假设钻速，求出切削参数，进而求出钻头受力，如果计算出的钻头受力与实际钻头受力相等，则假设钻速就是该力作用下的钻速，否则重新假设钻速，这样就可以根据受力预测钻速。根据上述模型和计算方法，编写了定向钻井PDC钻头的切削参数计算及钻速预测软件。

5 验证实例

5.1 设备和方法

为了验证上述切削参数计算方法的准确性，在中国石油大学（华东）XY-2B型定向钻井平台上进行了定向钻进实验（见图4）。用轴向加压装置给钻头提供钻压，用侧向加压装置给钻头提供侧向力。用压力传感器、扭矩传感器测定钻头的钻压、侧向力和扭矩，用位移传感器测定钻头的钻速。

图4 定向钻井实验装置

5.2 计算实例

在定向钻井平台上使用不同布齿的3种钻头，当钻压为30 kN，侧向力为3 kN时，实验测得的轴向和侧向钻速见表1。

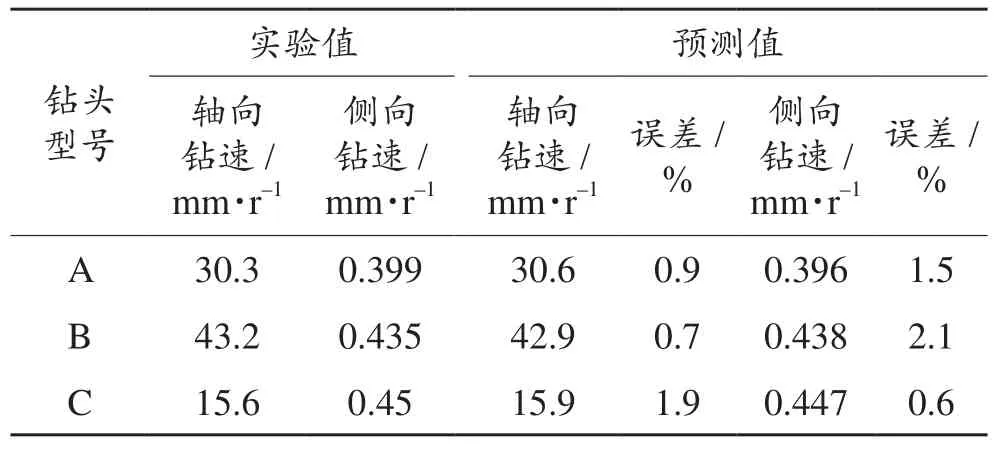
表1 实验值与预测值的比较

表2是当轴向钻速为1 mm/r，侧向钻速为0.1 mm/r时，计算出A钻头1号刀翼上各切削齿的切削参数。由图5可知，内锥上的1、3、5号切削齿的切削面积随钻头旋转角度Ω的变化趋势呈余弦函数形式，切削面积在Ω=180°时达到最大值，在Ω=0°或360°时达到最小值。同一刀翼上外锥上的10、15、20号切削齿的切削面积变化规律正好相反。这与实验观察到的情况吻合。

图5 1号刀翼各齿切削面积随旋转角度的变化关系

表2 试验钻头1号刀翼各切削齿的参数

6 结论

（1）运用空间解析几何理论和数值计算方法，分析了定向钻井PDC钻头在井底的运动状态，给出了切削齿的运动轨迹方程和切痕曲线方程。

（2）综合考虑了钻头的剖面形状、切削齿的布置、切削齿的工作角、切削齿的尺寸及切削齿切削的先后次序等因素的影响，提出了切削参数的数值计算方法。实例计算表明，模型和方法具有实用性。

［1］邹德永，王瑞和.PDC钻头的轨迹方程及切削参数计算方法［J］.石油钻采工艺，2003，25（5）：34-38.

［2］邹德永，张将海，王瑞和.PDC钻头力学模型试验研究［J］.石油钻探技术，2005，33（2）：41-43.

［3］MENAND S,SELLAMI H,SIMON C.How the bit profile and gages affect the well trajectory［R］.SPE 74459,2002.

［4］MENAND S,SELLAMI H.PDC bit classification according to anisotropic［R］.SPE 87837,2004.

［5］GERBAUD L,MENAND S,SELLAMI H.PDC bits： all comes from the cutter rock interaction［R］.SPE 98988,2006.

［6］DAGRAIN F,TSHIBANGU J P.Use of the D3 model for the estimation of forces acting on a cutter in rock cutting and drilling［R］.SPE 78242,2002.

（修改稿收到日期 2014-09-03）

〔编辑 薛改珍〕

Computing method for cutting parameters of PDC bit in directional drilling

ZOU Deyong1,WANG Jiajun1,YU Jinping1,GUO Yulong1,ZHAO Jian1,LU Wei2
（1.Petroleum Engineering College,China University of Petroleum（East China）,Qingdao266580,China;2.Huabei Oilfield Company,CNPC,Renqiu062552,China）

The optimized design of PDC bit for directional drilling and steering performance analysis need accurate calculation of cutting parameters like cutting area,cutting volume and cutting arc length of PDC cutting teeth.In line with different drilling tools-bent housing screw motor or pushing rotational steering system,this paper analyzed the motion status of PDC bit at bottom hole,established the trajectory of cutting teeth and cutting curvilinear equation.Also the numerical computing method was established for cutting area,cutting volume and cutting arc length of the cutting teeth according to bit deflection angle,complex bit motion,bit structure parameters and the sequence of cutting teeth,providing a analysis method for computerized optimal design of PDC bit and the analysis of steering performance of PDC bit.Practical calculation shows that the model and method are practical and can be further promoted.

PDC bit;cutting teeth;cutting parameters;trajectory;directional drilling

邹德永，王家骏，于金平，等.定向钻井PDC钻头切削参数计算方法［J］.石油钻采工艺，2014，36（5）：5-9.

TE249

：A

1000–7393（2014） 05–0005–05

10.13639/j.odpt.2014.05.002

国家“十二五”科技重大专项“薄互层低渗透油藏水平井优快钻井技术”的子课题“薄互层水平井导向PDC钻头优化设计及导向特性研究”（编号：05Z12020300）；中国石油大学（华东）校自主创新基金（编号：12CX06025A）。

邹德永，1962年生。2004年获得中国石油大学（华东）油气井工程专业博士学位，现从事油气井工程方面的教学与科研工作，教授、博士生导师。电话：18561409382。E-mail：upc-zoudy@163.com。