4点弯曲载荷作用下残余应力与弹性模量比对涂层/基体材料界面能量释放率的影响

杨班权，董 钊，陈学军，孙炜海

(1．装甲兵工程学院机械工程系，北京100072;2．北京科技大学数理学院应用力学系，北京100083)

基体表面的涂层(薄膜)材料发挥着重要的作用，如耐热、耐高温、耐腐蚀和耐磨损等［1］。工程应用中的多数涂层/基体材料，其涂层的寿命很大程度上决定了整个零部件或设备的寿命;而涂层/基体材料的典型失效模式是涂层与基体的界面开裂(或脱层)［2-3］，因此，涂层与基体的界面开裂行为研究具有重要的理论价值与实践意义。

若不考虑导致涂层与基体材料界面开裂的外界因素，如载荷条件和环境因素(高温、腐蚀、疲劳、摩擦磨损等)，抵抗涂层与基体间界面开裂的关键本征参数(或内因)是涂层与基体间的界面结合性能［2-3］，而涂层/基体材料的界面断裂行为分析是研究涂层/基体界面结合性能的基础。涂层与基体材料的界面结合性能研究中，4点弯曲方法仍然是目前最常用的方法之一［2］。关于涂层/基体材料的界面断裂行为研究目前已取得了不少成果［4-7］，但是这些研究成果多数情况下都没有考虑残余应力对界面断裂行为的影响。

由于在涂层材料的制备、前后热处理工艺或服役过程中，涂层与基体材料之间存在的晶格失配或热膨胀系数差异等问题导致界面不稳定，其表现形式为由于温度变化或外界载荷的作用导致涂层与基体之间的应变失配，这种失配会引起涂层内高达几十至几百兆帕的残余应力［8-10］，有时甚至会达到吉帕的量级［8-10］。这种量级的残余应力会导致薄膜产生严重的弯曲变形以致脆断失效，对涂层材料界面断裂行为的影响也十分明显［5］。

本文在考虑残余应力作用效应的基础上，采用ANSYS有限元计算方法，研究了在4点弯曲载荷作用下，残余应力与弹性模量比对涂层/基体材料界面能量释放率(裂纹扩展驱动力)及其相角的影响。

1 有限元力学建模及计算过程

在残余应力与4点弯曲载荷作用下，涂层与基体的界面断裂行为的力学模型如图1所示。

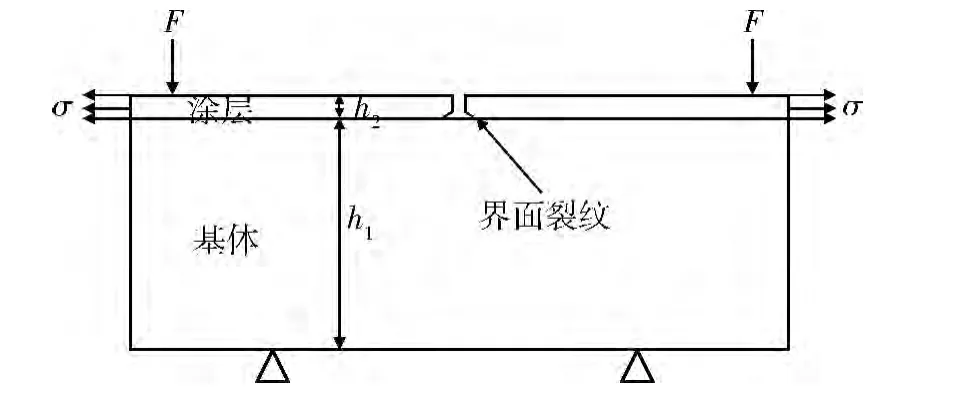
图1 残余应力与4点弯曲载荷作用下涂层/基体材料的界面断裂行为示意图

图1中:F为4点弯曲载荷;σ为残余拉应力，施加在涂层的横截面;h1为基体的厚度;h2为涂层的厚度。根据线弹性断裂力学理论，平面应变下的裂纹尖端能量释放率的计算公式为［11］

式中:ν1、ν2分别为基体和涂层的泊松比;G1、G2分别为基体和涂层的剪切模量;ε为参数，

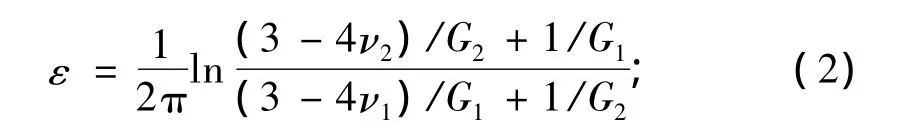
式(3)中，ψ为相角(与材料界面结合性能有关的参数)，

ω=φ-εln r，为幅角，φ为用复数表示的位移幅角，r为节点到裂纹尖端的距离，β=arctan(2ε)，为角度，

其中

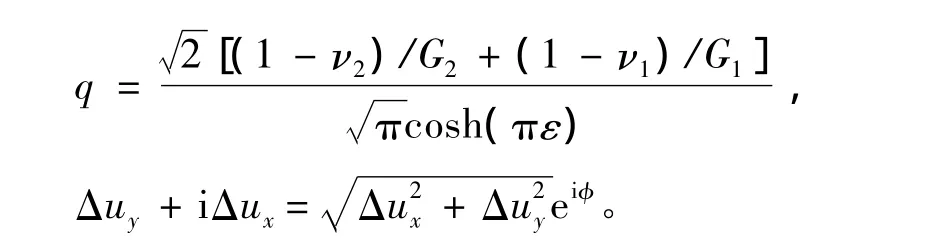
建模过程中，选取电镀铬涂层/钢基体材料为研究对象。电镀铬涂层广泛应用于枪、炮身管的内壁中，具有耐热、耐磨损和耐腐蚀的特点。这里，铬涂层的厚度 h2=150μm，涂层的弹性模量为 E2=280 GPa，ν2=0．22;基体的弹性模量为E1=210 GPa，ν1=0．28，厚度 h1=2 mm;残余应力 σ =250 MPa。

在有限元建模计算过程中，采用PLANE182单元。根据图1的力学模型，采用ANSYS建立有限元计算模型，如图2所示。

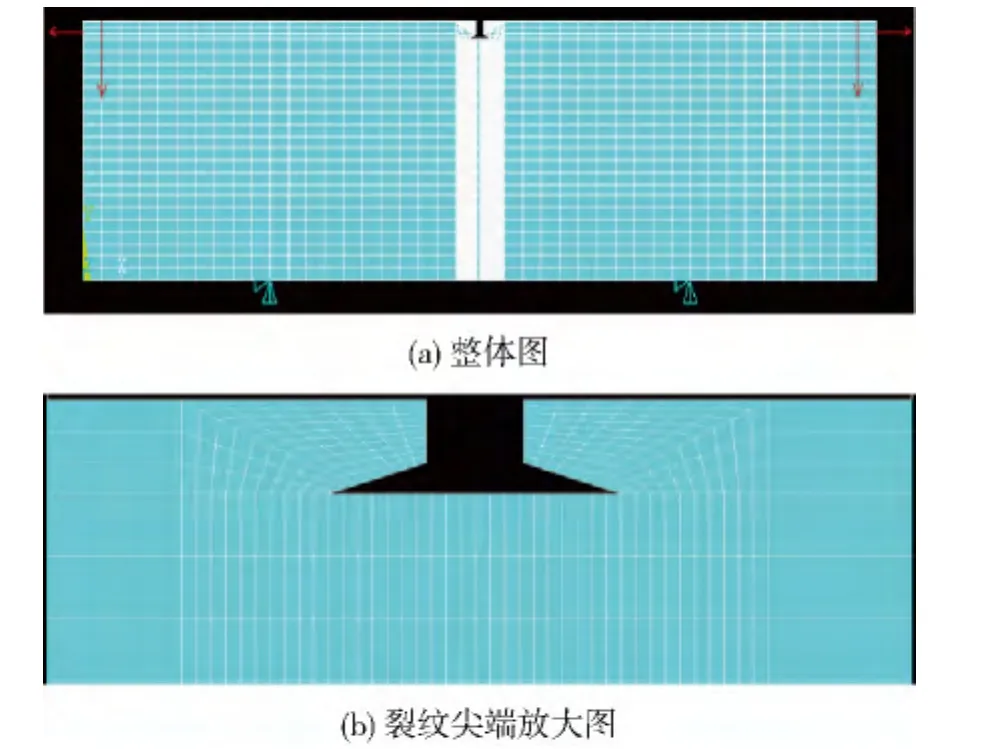
图2 有限元计算模型

2 计算结果及其分析

应用ANSYS10．0建模分析，首先得出裂纹尖端附近节点位移;然后计算裂纹尖端的能量释放率。计算过程中，分析了网格划分密度对计算结果的影响，划分的网格密度有足够的精度以保证计算结果的正确性。加载后的变形、应力云图如图3所示。

图3 加载后的变形、应力云图

由图3可见:在对称载荷作用下，结构变形、应力分布表现出对称特征，在裂纹的尖端附近出现了明显的应力集中现象。由于结构变形及应力分布特征的对称性，选取裂纹尖端的一半为例进行研究。

依次改变涂层厚度、弹性模量、残余应力的大小，分别建立不同弹性模量比E2/E1、不同残余应力的ANSYS模型，记录每次计算的节点位移和应力，研究残余应力与弹性模量比对涂层/基体材料界面能量释放率及其相角的影响，如图4-7所示。

由图4可见:残余应力对能量释放率的影响十分明显，随着残余拉应力的增大，能量释放率将增大，因此残余拉应力将促使裂纹扩展;反之，可通过减小残余压应力来降低能量释放率，抑制裂纹的扩展。

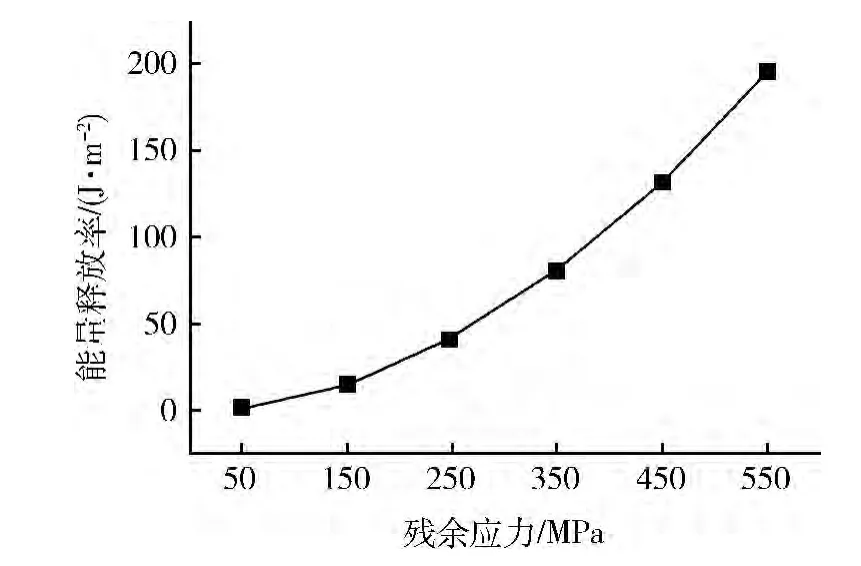
图4 残余应力对能量释放率的影响

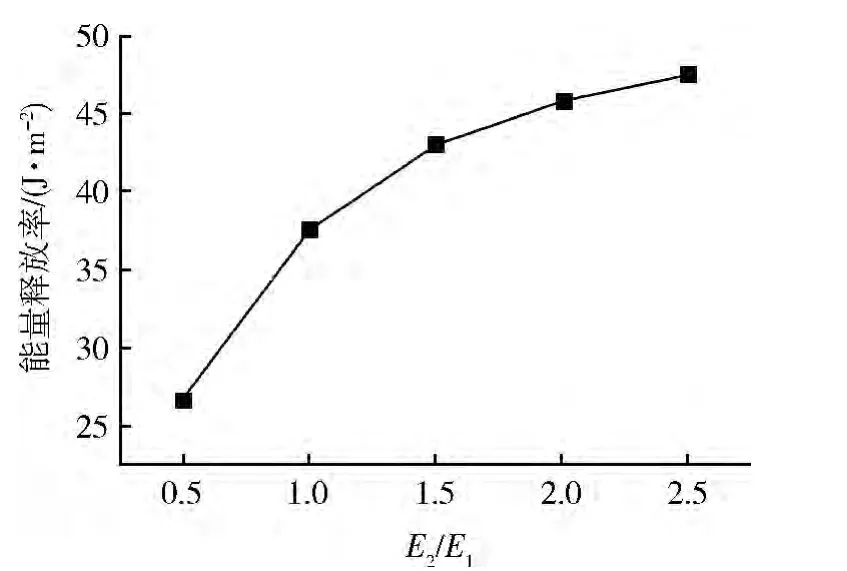
图5 弹性模量比对能量释放率的影响

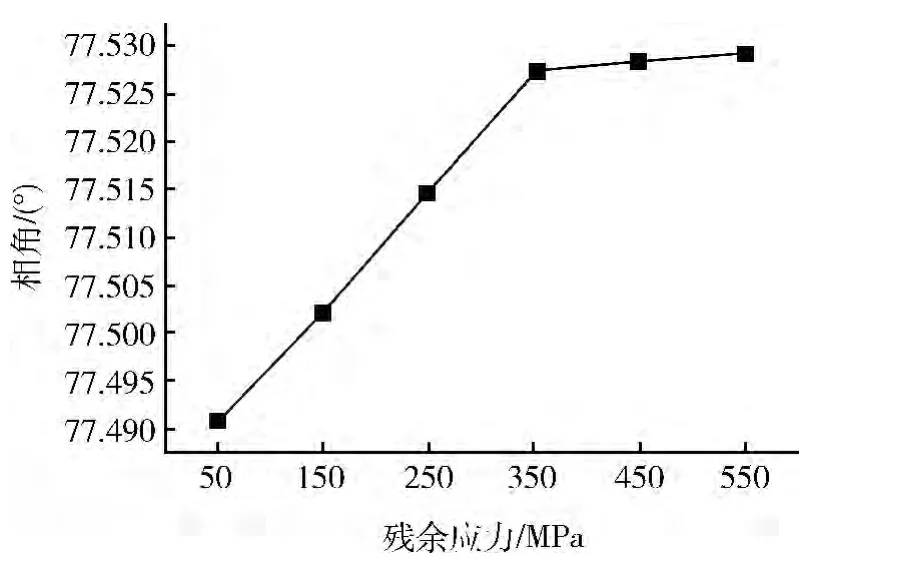
图6 残余应力对相角的影响

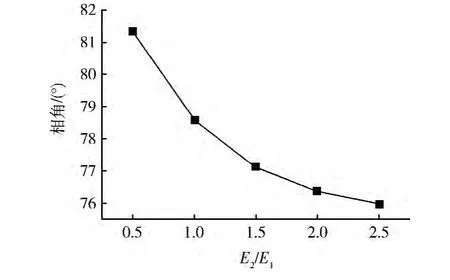
图7 弹性模量比对相角的影响

由图5可见:弹性模量比对能量释放率也有影响，能量释放率随着弹性模量比的增大而增大。

由图6可见:能量释放率中的相角随着残余拉应力的增大而增大，但是影响不是十分显著。

由图7可见:能量释放率中的相角随弹性模量比的增大而减小，但与残余应力对相角的影响程度相比，弹性模量比对相角的影响比较显著。

3 结论

本文在考虑残余应力效应的基础上，研究了4点弯曲载荷作用下残余应力和弹性模量比对涂层/基体材料界面能量释放率及其相角的影响。本文的计算结果适用于厚涂层/基体材料体系，且假定残余应力沿着横截面均匀分布。下一步将对微/纳米尺度下，考虑梯度残余应力效应的单层膜/基体材料或多层膜结构材料的界面断裂行为与界面结合性能进行深入研究。

［1］ Freund L B，Suresh S．Thin Film Materials，Stress，Defect Formation and Surface Evolution［M］．Cambridge:Cambridge University Press，2003:1-6．

［2］ Volinsky A A，Moody N R，Gerberich W W．Interfacial Toughness Measurements for Thin Films on Substrates［J］．Acta Materialia，2002，50(3):441-466．

［3］ Chou T L，Yang SY，Wu CJ，et al．Measurement and Simulation of Interfacial Adhesion Strength Between SiO2Thin Film and III-V Material［J］．Microelectronics Reliability，2011，51(9/11):1757-1761．

［4］ Lin M J，Chen R S．Effect of Gradient Residual Stress on Adhesion for a Center-anchored Circular Plate and Its Underlying Substrate［J］．Sensors and Actuators A，2004，115:109-117．

［5］ Matin M A，Ozaki K，Akai D，et al．Correlation Between Residual Stresses and Bending in Functional Electroceramic-based MEMS Actuator［J］．Computational Materials Science，2014，85:253-258．

［6］ Fu Y Q，Du H J，Sun C Q．Interfacial Structure，Residual Stress and Adhesion of Diamond Coatings Deposited on Titanium［J］．Thin Solid Films，2003，424(1):107-114．

［7］ Nie P L，Shen Y，Chen Q L，et al．Effects of Residual Stresses on Interfacial Adhesion Measurement［J］．Mechanics of Materials，2009，41(5):545-552．

［8］ Zheng X J，Li JY，Zhou Y C．X-ray Diffraction Measurement of Residual Stress in PZT Thin Films Prepared by Pulsed Laser Deposition［J］．Acta Materialia，2004，52:3313-3322．

［9］ Ohno T，Fu D，Suzuki H，et al．Residual Stress in Lead Titanate Thin Film on Different Substrates［J］．Journal of the European Ceramic Society，2004，24:1669-1672．

［10］ Benegra M，Lamas D G，Fernández M E．et al．Residual Stresses in Titanium Nitride Thin Films Deposited by Direct Current and Pulsed Direct Current Unbalanced Magnetron Sputtering［J］．Thin Solid Films，2006，494:146-150．

［11］ Hutchinson J W，Suo Z．Mixed Mode Cracking in Layered Materials［J］．Advances in Applied Mechanics-transactions of the ASME，1992，29:63-191．