空投设备气囊缓冲系统的缓冲特性分析与匹配方法

吕哲源，王红岩，洪煌杰，李建阳，芮 强

(1．63901部队，北京100072;2．装甲兵工程学院机械工程系，北京100072)

气囊缓冲系统被广泛应用于货物或装备的空投着陆、航天器回收、无人机及导弹回收等存在较大冲击过载的领域。通过气囊压缩排气，可进一步降低空投设备的着陆速度，使冲击过载控制在允许范围内，同时不出现反弹和倾覆现象，保护空投设备及仪器［1］。目前，国内外研究人员建立了很多缓冲气囊模型，分析手段基本上可以分为2类，即解析分析方法和有限元方法。Escar等［2］从热力学方程出发，建立了缓冲气囊的解析分析模型，并讨论了主要气囊参数之间的相互影响关系;温金鹏等［3］考虑气囊织布弹性的影响，建立了缓冲气囊的物理解析分析模型，并对气囊缓冲特性进行了研究;牛四波等［4］建立了双气室气囊的解析分析模型，并对气囊参数进行了优化。A．P．Taylor［5］采用显式有限元方法对重装空投的气囊缓冲技术进行了仿真分析;洪煌杰［6］和李建阳［7］利用有限元方法对空降车气囊缓冲特性及着陆过程中车体结构冲击响应进行了研究。

然而，以上研究所建立的气囊缓冲过程数学模型主要是基于物理方程建立的，计算过程较复杂。为了使气囊缓冲过程的计算更简便，笔者将气囊缓冲系统各参量无量纲化，从而建立气囊缓冲系统的无量纲动力学模型，并基于此模型对气囊缓冲系统参数匹配设计方法进行研究。

1 气囊缓冲系统的无量纲动力学建模

1．1 气囊缓冲系统模型简化

气囊缓冲过程的建模基于如下假设:1)气囊织布是柔性的，但不可拉伸，在气囊压缩过程中，只有气囊高度发生变化，而忽略其横截面形状和触地面积的变化;2)缓冲过程中忽略降落伞阻力的影响;3)整个缓冲着陆过程，气囊内空气压缩为等熵压缩;4)整个载荷-气囊系统垂直下落;5)囊内气体为理想气体;6)若无特别说明，排气口的开启压力为1个大气压;7)受气囊织布厚度和下落时空气阻力的影响，气囊实际压缩高度为其初始高度的85%。

气囊缓冲的机理是:气囊内部气体压缩并吸收载荷的冲击能量，压缩气体经气囊排出释放能量，从而达到减小冲击过载、使载荷安全着陆的目的。基于以上分析和假设，笔者根据排气口流量方程和载荷运动方程来建立气囊的着陆缓冲过程数学模型。

1．2 排气口气体流量方程

气囊缓冲过程如图1所示，以竖直向下方向为坐标轴的正方向。在不考虑气囊织物泄漏的情况下，单位时间内气囊由排气口对外排出的气体应该与囊内气体减少的质量相等，可写为

式中:ρt为气囊排气口处的气体密度;An为排气口面积;K为流量系数;ct为气体流速;ρ为囊内气体密度;h为气囊高度;A为气囊底面积;t为时间。

图1 气囊缓冲过程

根据理想气体状态方程，有

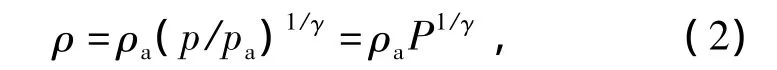
式中:ρa为外界的空气密度;p为囊内气体压强;pa为外界大气压强;P为气囊内外压力比;γ为绝热系数，对于空气，γ =1．4。

1．3 载荷运动方程

垂直下落的载荷-气囊系统根据受力平衡可得

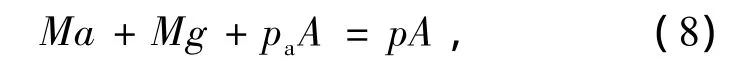
式中:M为载荷质量;a为缓冲过程载荷的加速度;g为重力加速度。

在气囊缓冲过程中，任意时刻载荷的速度和加速度方程可分别表示为

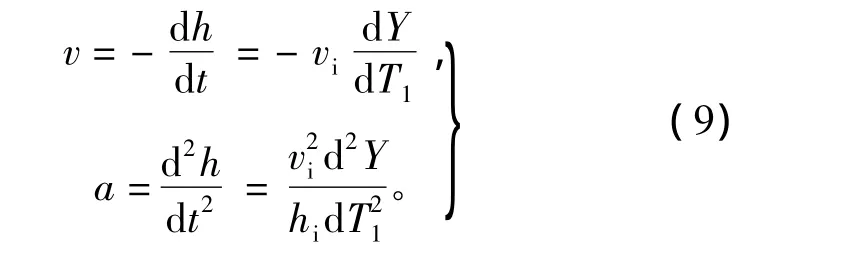
引入2个无量纲参量:无量纲气囊高度参量H和无量纲气囊载荷参量Z。

将式(9)、(10)代入式(8)，化简整理后可得无量纲形式的载荷运动方程为

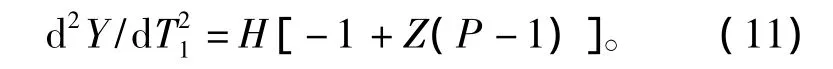
1．4 无量纲数学模型

由以上分析可知，气囊的着陆缓冲过程无量纲动力学数学模型为

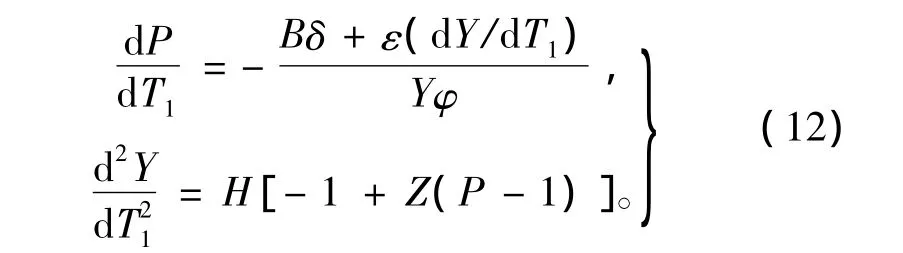
为便于处理仿真计算结果，得到更具实用性的气囊，定义反映气囊缓冲性能的3个重要指标［8］:

1)最大加速度的值用Ng表示，N为任意数字，通常满足空投系统性能要求的系统最大加速度为5g～16g，即5≤N≤16;

2)着陆冲击末速度与着陆初速度之比用σ表示，称为无量纲速度参量，通常要求气囊着陆冲击末速度不超过着陆初速度的1/2，即σ≤0．5;

3)通常要求气囊缓冲系统着陆缓冲过程所需的无量纲时间T1≤3。

2 匹配设计图的构造与应用

2．1 匹配设计图的构造

由无量纲数学模型可知:只需已知H、Z、B这3个变量，就可以通过仿真计算得到N、σ和T1这3个反映气囊缓冲性能的缓冲特性参数。

气囊缓冲系统匹配设计图的构造流程如图2所示，下面通过一个例子来进行详细说明。

设 Z=10，H 的范围为(0，0．5)，B 的范围为(0，2．4)。令 H=0．130，按照0．01 的比例依次增加B的值，得到(0，2．4)范围内每个B值所对应的一组(N，σ，T1)，最终得到气囊缓冲性能参数(N，σ，T1)随排气口参量B的变化曲线，如图3所示。

根据有效气囊的限定条件，在图3中标出了N=5，16，σ =0．5以及 T1=3的位置，从而得到了有效气囊排气口参量B的范围。从图3中还可得出N=5，6，8，10，12，14，16，T1=2，3，σ =0．2，0．3，0．4，0．5时，这些特征点所对应的B值。

同样地，对于不同的气囊高度参量H，可以得到气囊缓冲性能参数随H的变化曲线，进而也可以得到这些特征点所对应的H值。

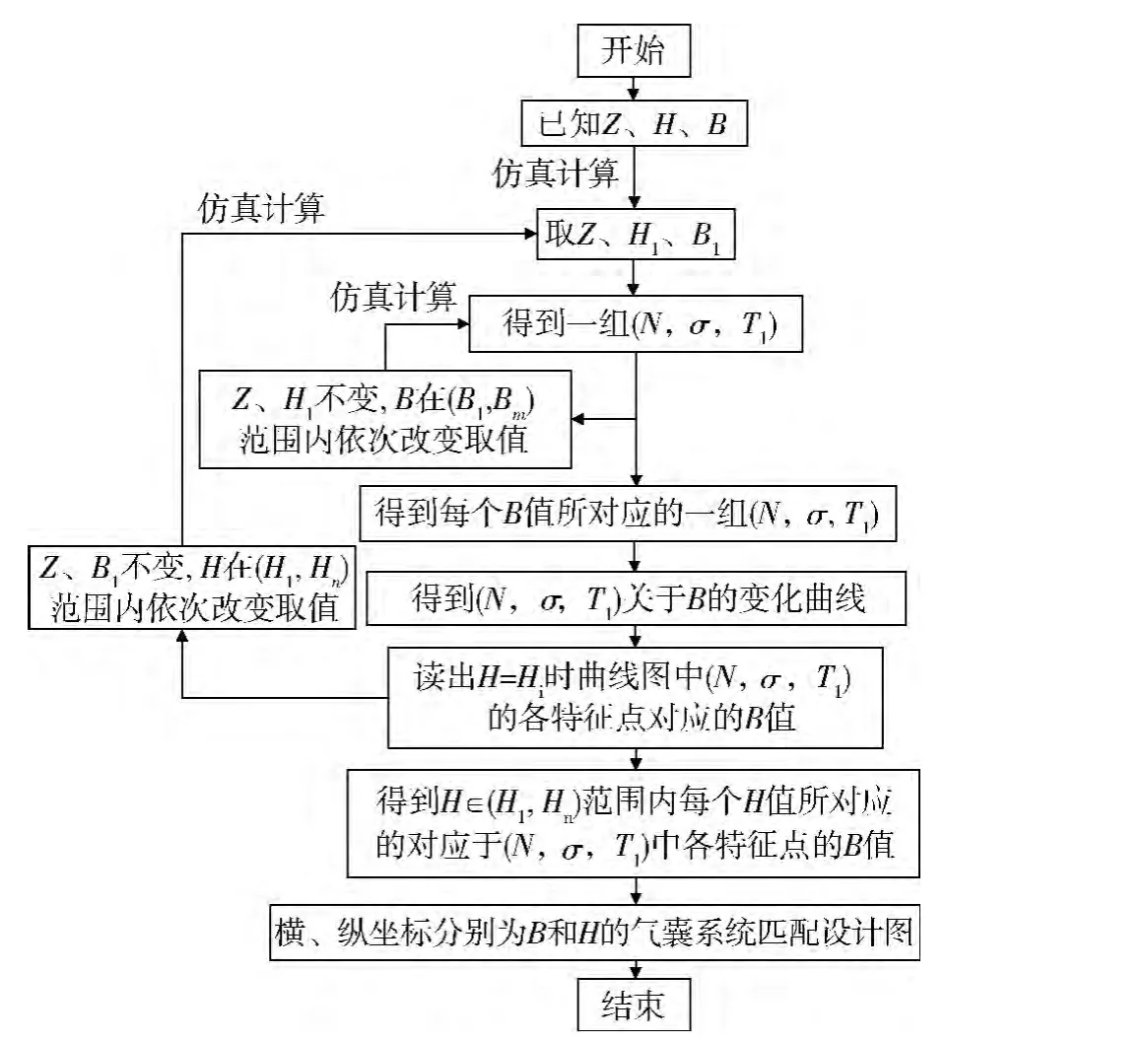
图2 匹配设计图的构造流程

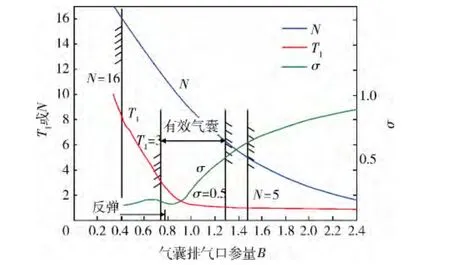
图3 缓冲性能参数随排气口参量B的变化曲线

以B为横坐标，H为纵坐标，将每个H值所对应的对应于(N，σ，T1)中各特征点的B值在坐标图中进行标记，最终得到Z=10，限定范围为5≤N≤16、σ≤0．5和T1≤3的气囊匹配设计图如图4所示。

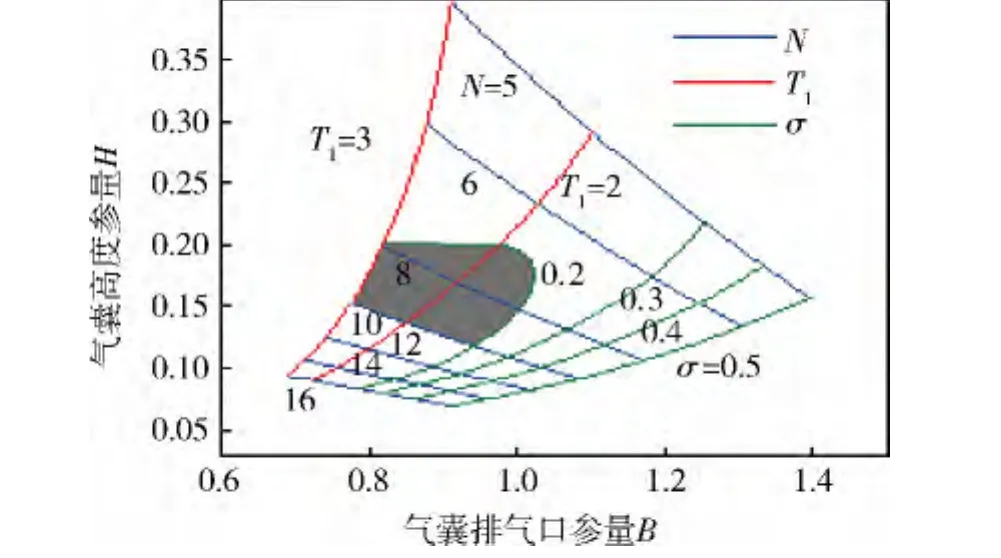
图4 气囊匹配设计图(Z=10)

2．2 匹配设计图的应用

根据载荷参量Z的不同，可以得到不同的气囊匹配设计图，图中的曲线包含了N、T1和σ这3个主要体现气囊缓冲特性参数的信息。下面通过一个例子来具体说明匹配设计图的应用。

已知载荷质量为672 kg，气囊底面积为0．65 m2，着陆初速度为7．5 m/s，载荷所能承受的最大加速度和最大着陆冲击末速度分别为10g和1．5 m/s。

首先计算出无量纲的载荷质量参量Z=10，因此，对应的气囊匹配设计图为图4。

根据载荷的性能要求，即N≤10，σ≤0．2，可知图中阴影部分区域中的点均能满足该性能要求。从中任意取一点，如N=10和σ=0．2这2条曲线的交点(0．942，0．118)，即 B=0．942，H=0．118，将 B、H 分别代入式(6)、(10)中可得:An=0．016 m2，hi=0．677 m，即排气口面积为 0．016 m2、高度为0．677 m的气囊能满足此性能要求。

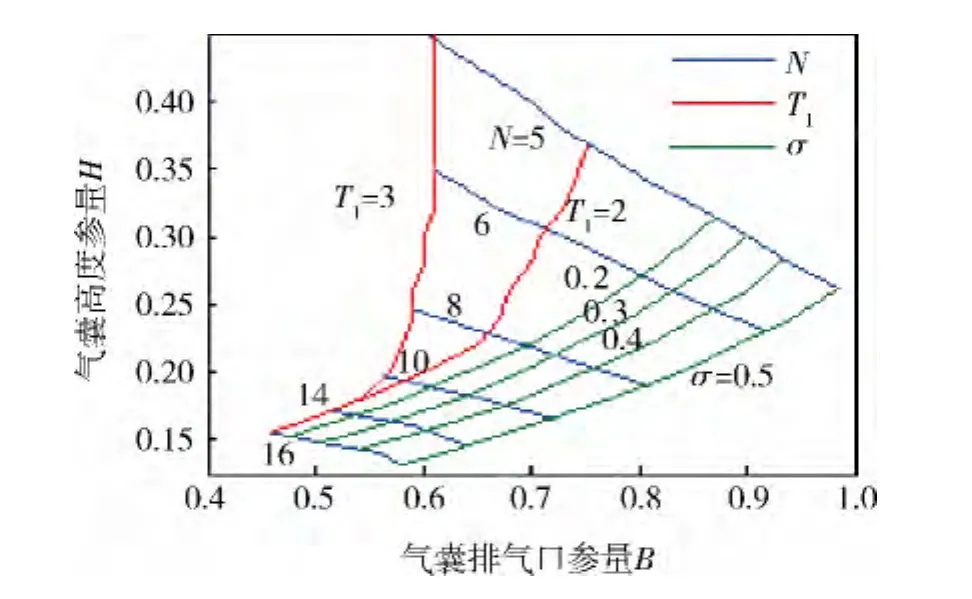
图5 气囊匹配设计图(Z=3．75)

3 相关影响因素的分析

3．1 排气口面积的影响

由式(6)可知:An与B成正比。从图4中可以看出:随着B的减小，N和T1都逐渐变大，而σ逐渐减小。即随着气囊排气口面积的减小，缓冲过程的最大加速度和压缩时间都逐渐增大，而着陆末速度逐渐减小。

3．2 气囊高度的影响

由图4可知:H的变化对N和σ的影响较大，而对T1的影响较小。由式(6)可知:hi与H成正比;hi及T1均与缓冲过程实际压缩时间t成正比。因此，hi越高，最大加速度和着陆末速度都越小，而实际压缩时间会有所增加。

3．3 着陆初速度与载荷的影响

一个理想的气囊应该能用在不同的载荷-气囊系统中，且能使气囊的缓冲特性满足在一定范围内变化，即当着陆初速度或载荷大小发生一定变化时，缓冲过程的最大加速度和着陆末速度不应发生太大的变化。

为了分析载荷对缓冲性能的影响，分别给出Z=3．75和Z=30时气囊的匹配设计图，如图5、6所示。

将图4-6边界区域组成的近似菱形画在同一幅图上，如图7所示。可以看出:随着Z的增大，有效气囊的参数范围变得更宽，任取一点P，从图中可以近似得出 Z=3．75，10，30 时的(N，σ，T1)，分别为(5，0．5，＜2)、(6，0．25，2．5)和(8，0．2，＞3)。说明若载荷过小，则最大加速度较大，压缩时间较长;若载荷过大，则着陆冲击末速度较大。

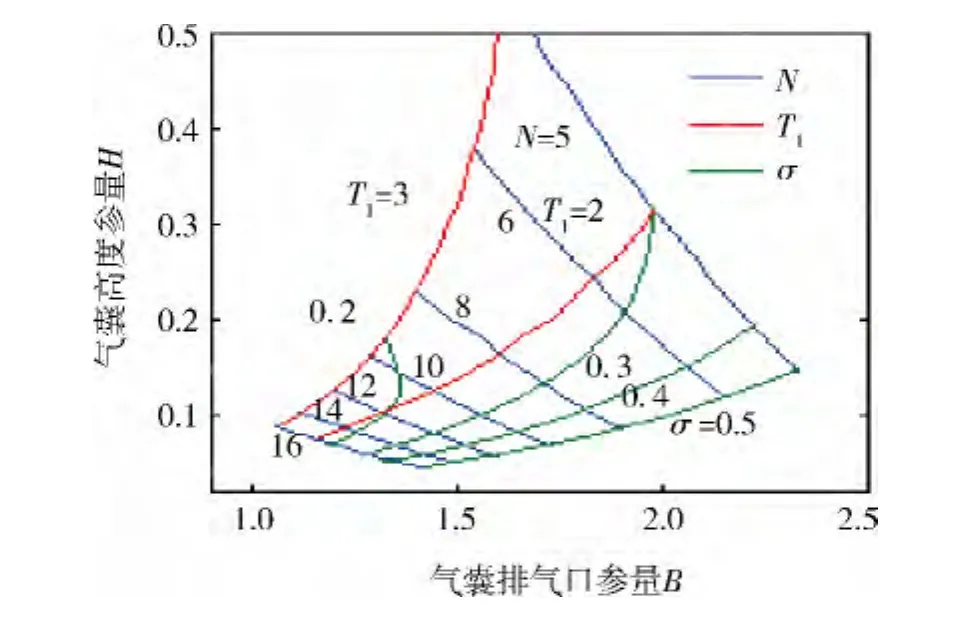
图6 气囊匹配设计图(Z=30)

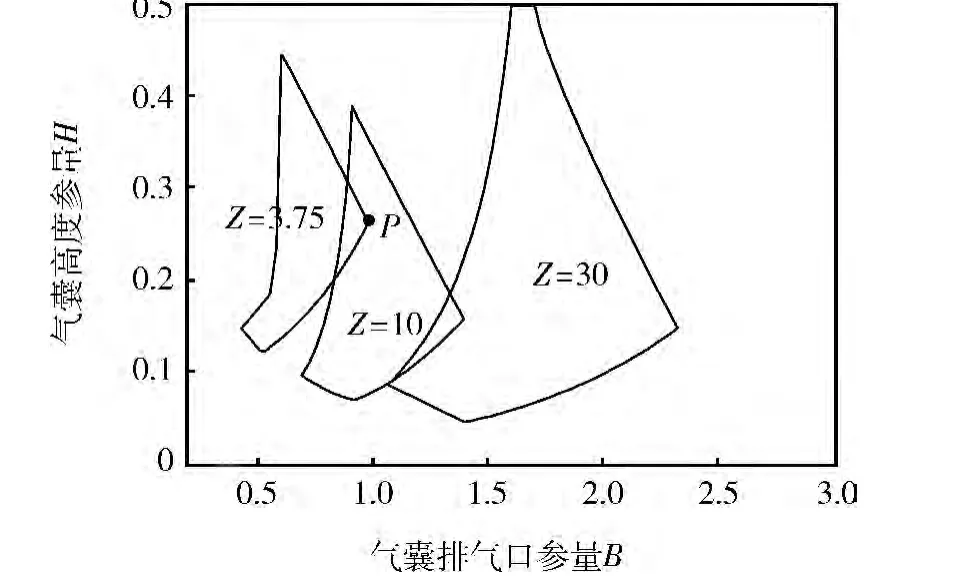
图7 不同载荷参量的匹配设计图

将一载荷-气囊系统的各已知参量无量纲化，可得 Z=10，H=0．13，B=0．887。将载荷质量和着陆初速度同时改变±20%，得到着陆初速度和载荷质量变化的气囊缓冲特性曲线，如图8所示。

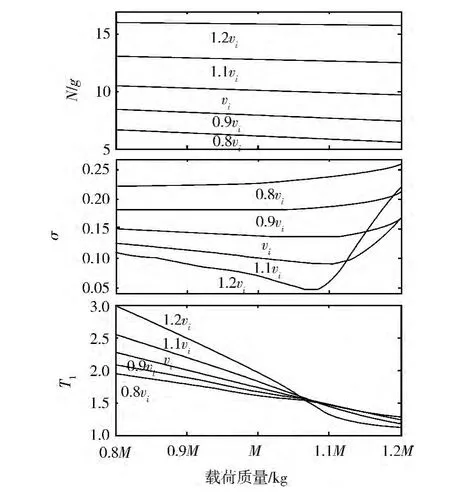
图8 载荷质量和着陆初速度对缓冲性能的影响

由图8可知:载荷质量的变化对最大加速度影响很小，而着陆初速度对最大加速度的影响较大，因此，在空投过程中应尽量控制载荷-气囊系统的着陆初速度;载荷质量增加10% ～20%，同时着陆初速度增加10% ～20%，着陆末速度比预期的更大;对于着陆初速度大、载荷质量小的气囊，气囊缓冲过程的时间很长，且载荷很容易反弹;压缩时间随着载荷质量的增大而减小，且载荷质量越大，着陆初速度对压缩时间的影响越小。

3．4 气囊底面积的影响

由式(6)、(10)可知:气囊底面积A与B成反比，与Z成正比。由3．3的分析可知:最大加速度随着B的增大而减小，随着Z的增大而增大。因此，随着A的增大，最大加速度也逐渐增大。

3．5 气囊排气口开启压力的影响

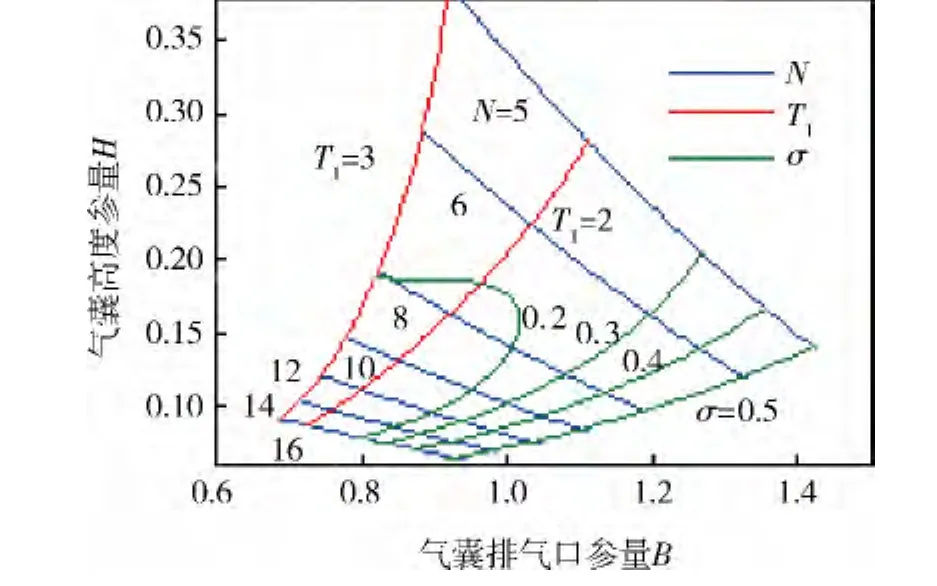
图9 排气口开启压力为1．3个大气压的匹配设计图(Z=10)

图9为Z=10，排气口开启压力为1．3个大气压时的气囊匹配设计图，与图4对比，可知两者几乎没有区别，说明增大排气口开启压力对气囊缓冲性能几乎没有影响，因此，通常采用气囊排气口没有用遮盖片盖住(开启压力为1个大气压)的气囊。

3．6 气囊高和直径之比的影响

由3．2和3．4的分析可知:最大加速度随气囊初始高度的增大而减小，随气囊底面积的增大而增大。因此，气囊高和直径之比越大，则整个载荷-气囊系统在着陆缓冲过程中受到的最大加速度越小。但这个比值也不是越大越好，若比值过大，则气囊在压缩过程中容易因弯曲而导致翻覆，从而对载荷造成更大的损害。因此，应该对气囊高和直径之比做一个限定。通过查阅试验资料［9］可知，在实际应用中这个比值很少超过1．5。

3．7 能量效率分析

气囊缓冲系统作为着陆缓冲设备，其作用是在着陆缓冲过程中吸收空投系统的能量。因此，其能量效率可定义为载荷-气囊系统在缓冲过程中损失的能量与系统着陆过程的初始能量的比值，可写为

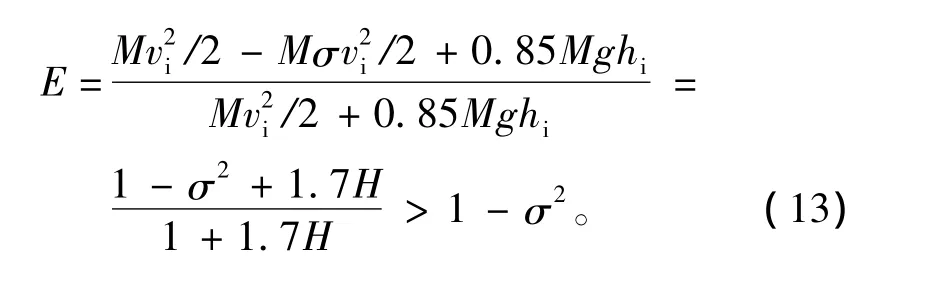
4 气囊匹配设计方法和实例验证

4．1 气囊匹配设计方法

在设计气囊前，应已知载荷-气囊系统的以下信息:1)载荷质量;2)气囊所能设计的最大底面积;3)着陆初速度;4)缓冲过程系统所能承受的最大加速度;5)系统能承受的最大着陆末速度。

关于气囊缓冲系统的设计，需考虑以下方面。

1)根据载荷的质量和最大底面积，能算出单位面积气囊所承受的最小载荷质量，通常，能满足实际应用的气囊单位面积所承受的载荷范围为500～1 700 kg/m2。

2)载荷和气囊的强度必须能承受着陆末速度为3 m/s时受到的撞击。

3)若着陆初速度小于6 m/s，则可能需要多个降落伞，此时，降落伞本身的重力在设计时也应该予以考虑;若系统的着陆初速度大于9 m/s也是不合理的，除非载荷和气囊都能承受此着陆初速度下的着陆末速度。

4)气囊缓冲系统根据气囊个数和直径的不同会有很多种组合方式，假设一个气囊缓冲系统中所有气囊都相同，则系统中的每个气囊承受的载荷也是相同的。因此，可以计算出系统中单个气囊单位面积所承受的载荷，并以此来判断该气囊缓冲系统是否符合设计要求。

5)根据之前设定的气囊单位面积所承受的载荷范围和避免气囊翻覆所要求的气囊高与直径之比的范围来选择气囊，这就确定了所设计的气囊不会翻覆或者产生剧烈的撞击反弹。

6)经过以上步骤后，如果还有气囊缓冲系统方案可供选择，应该选择气囊数量多的气囊缓冲系统，因为此时气囊织布所受的张力更低。

7)通过相应的数学模型计算得到气囊的匹配设计图，在图中选择合适的参量B和H的值，从而可以计算出气囊的排气口面积和高度。此时还应检查计算得到的气囊高度是否满足小于1．5倍气囊直径的设计要求。

8)气囊织布不能太厚，否则气囊不容易压缩折叠，气囊上应该附有几条加强带来增加气囊的强度，同时，排气口应均匀分布在气囊的四周。

4．2 实例验证

已知某空投设备重1 150 kg，底面长、宽分别为1．2 m 和 1．1 m，着陆初速度约为 8．4 m/s，能承受的最大着陆冲击末速度和最大加速度分别为2．4 m/s和13g。气囊匹配设计方法如下。

1)单位面积气囊承受的最小载荷为1 150/(1．2 ×1．1)=872．1 kg/m2，在所承受的载荷范围内。

2)气囊缓冲系统可能由1～12个气囊组成，根据4．1中气囊缓冲系统设计需考虑的方面5)，排除了很多的可能性。气囊选择明细如表1所示。

3)由表1可知:只有单个气囊和由4个气囊组成的气囊缓冲系统满足5)的要求。

4)为了使气囊承受的织布张力更低，选择由4个气囊组成的气囊缓冲系统。

5)该气囊缓冲系统单个气囊所承受的载荷为287．5 kg，气囊直径为 0．55 m，因此 Z=8．54，通过计算可以得到气囊高度hi=0．73 m，排气口面积An=0．005 84 m2。此时，气囊高和直径之比为1．33＜1．5，因此满足设计要求。

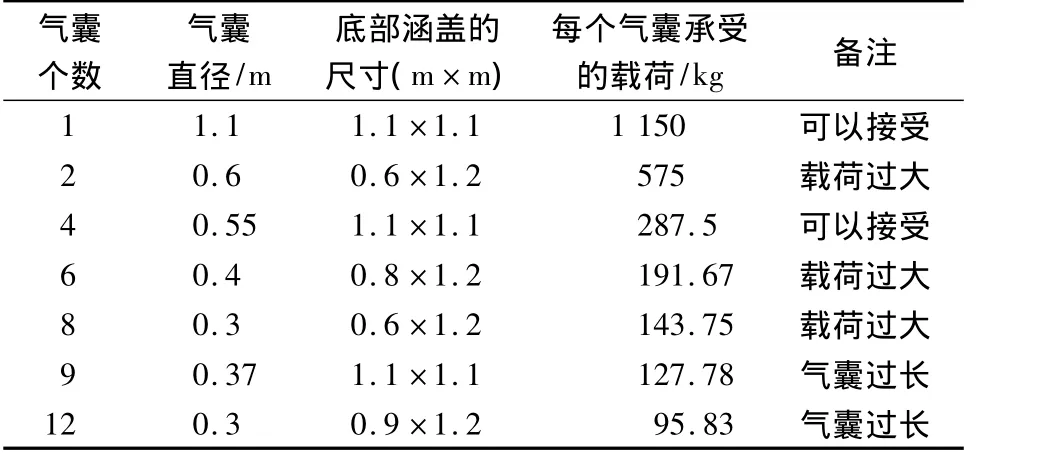
表1 气囊选择明细

5 结论

1)通过解析分析法建立了无量纲的空投设备气囊缓冲过程数学模型，并根据此模型构造了气囊的匹配设计图。

2)气囊排气口面积、气囊高度、气囊底面积、着陆初速度和载荷均对气囊的缓冲性能有一定的影响，而气囊排气口的开启压力对缓冲性能的影响几乎可以忽略不计。

3)通过一个具体例子说明了空投设备气囊缓冲系统的参数匹配设计方法，该方法可以为空投设备气囊缓冲系统的匹配设计提供技术支持。

［1］ 尤因E G，纳克T W，比克斯比H W．回收系统设计指南［M］．北京:航空工业出版社，1988:376-381．

［2］ Escar JB，Morgan W C．Technical Report R-75［R］．USA:Lewis Research Center，1961．

［3］ 温金鹏，李斌，谭德伟，等．考虑织布弹性的软着陆气囊缓冲特性研究［J］．振动与冲击，2010，29(2):79-83．

［4］ 牛四波，王红岩，迟宝山．空投设备的缓冲气囊优化设计［J］．装甲兵工程学院学报，2010，24(5):36-40．

［5］ Taylor A P．Investigation of the Application of Airbag Technology to Provide a Softlanding Capability for Military Heavy Airdrop［C］∥AIAA 2001-2046．2001:284-292．

［6］ 洪煌杰．空降车气囊缓冲系统特性分析及参数优化［D］．北京:装甲兵工程学院，2010．

［7］ 李建阳．空降车落地缓冲过程结构冲击响应研究［D］．北京:装甲兵工程学院，2010．

［8］ Browning A C．A Vertical Approach to Airbag Shock Absorber Design［R］．USA:Ministry of Aviation Aeronautical Research Council，1963．

［9］ 吕哲源，王红岩，迟宝山，等．重型装备回收系统气囊缓冲特性研究［J］．装甲兵工程学院学报，2011，25(3):39-43．