基于单变量多目标规划的装甲车辆冷却系统智能化控制
冉光政,骆清国,尹洪涛,李顺达,陈 中
(1.装甲兵工程学院机械工程系,北京100072;2.总装备部武汉军代局驻郑州地区军代室,河南郑州450047)
新一代装甲车辆推进系统具有功率密度高与机电混合传动2大主要特征,装甲车辆动力舱内热部件也形成了热部件多、散热量大与目标温度范围广等特点。然而,由于受动力舱空间布置等多因素的限制,其冷却系统只能通过调节风扇转速来调节冷却强度。由此产生了如何通过单一的变量控制,最大限度地保证多个热部件工作在合理的温度范围的控制难题。目前,针对民用车辆的冷却控制研究较多,文献[1]将载重汽车发动机冷却风扇的传统驱动方式改为电动机驱动,并采用自动控制技术进行控制,取得了很好的控制效果;文献[2]采用PID算法开发了汽车发动机冷却控制系统,提高了冷却系统温度调节精度。对于军用车辆的冷却控制研究,文献[3]提到了模糊控制算法在军用车辆发动机智能化控制冷却系统中的应用,但其研究对象较为简单,且未涉及满足多目标的情况。为解决新一代装甲车辆推进系统冷却难题,本文将冷却系统抽象为单变量多目标规划问题,提出一种基于单变量多目标数学规划与模糊智能控制算法相结合的解决办法。
1 冷却方案与数学建模
1.1 冷却系统结构及控制方案
目前,装甲车辆推进系统的冷却系统通常采用间接冷却的方式,即采用一种液体在热源处吸收热量,而后在另一位置(散热器)将热量散发给大气。因此,液体循环系统和风道是构成液冷式冷却系统的2个基本子系统[4]。图1为某机电混合传动推进系统的冷却系统结构原理图(图中数字为热部件的序号)。由于机电混合传动推进系统涉及的热源工作温度范围广,因此通常采用高、低温双循环冷却液回路的结构进行冷却散热。低温循环中冷却液被泵出后,首先进入工作温度较低的电池冷却器,而后分2路,一路经过二级中冷器、机油冷却器,另一路经过电机冷却器(集成了发电机及其控制器和电动机及其控制器的冷却)、传动油冷却器,2路汇合将吸收的热量带入低温散热器,由冷却空气带走。高温循环中冷却液在泵的驱动下,将并联的2个热源(一级中冷器与柴油机本体)的热量带入高温散热器,由冷却空气带走。风道为吸风式风道,空气进入百叶窗后先经过低温散热器,后经过高温散热器。
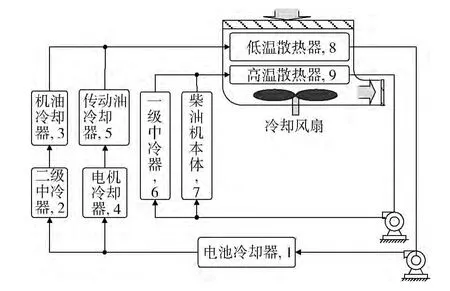
图1 冷却系统结构原理图
冷却系统工作时,传感器将采集到的各热部件工况反馈到控制单元,控制单元结合环境因素和热部件工况,按照一定的控制策略与算法调节冷却风扇转速,使冷却系统中各热部件在不同环境和不同工况下具有适宜的工作温度。图2为冷却系统控制原理图。
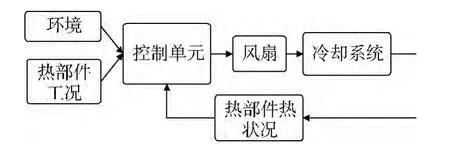
图2 冷却系统控制原理图
根据推进系统工作原理可知:冷却系统中的一级中冷器、二级中冷器与机油冷却器的散热量与柴油机本体的散热量变化趋势相同,都随柴油机的功率增大而增大;传动油和电机冷却器的散热量变化趋势相同,同时也受柴油机工况影响;电池冷却器的散热量较小,但要求较低的工作温度。因此,该冷却系统是一个热部件散热规律不同、工作温度不同、相互间有串联也有并联关系的复杂系统,而高、低温散热器串联,调节风扇转速会同时影响2个散热器。
1.2 冷却系统的数学模型
准确的冷却系统数学模型是进行多目标数学规划的前提。对于冷却系统中除低、高温散热器外的热部件i(i=1,2,…,7),定义其在 t时刻散热量为Qi(t)(kW),冷却液流量为qli(t)(kg/s),入口温度为Tlini(t),出口温度为Tlouti(t),热部件的目标温度(冷却液出口处)为 Tgi,冷却液比定压热容为cp1。则根据传热原理(忽略管道的壁面热损失),有
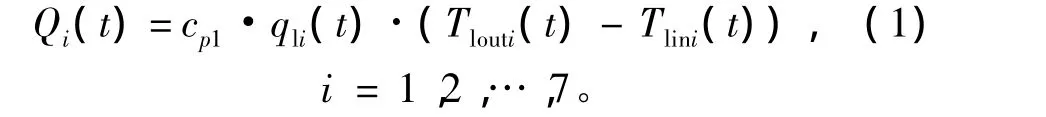


2 单变量多目标数学规划与求解
2.1 单变量多目标数学规划的提出
冷却系统的控制目标是最大限度地保证系统中各个热部件工作在其最佳工作温度范围,因此控制时需确定合适的冷却风量,由此产生了1个变量7个目标的数学规划问题[5]:

表1给出了各个热部件的允许温度范围、最佳温度范围与目标温度。
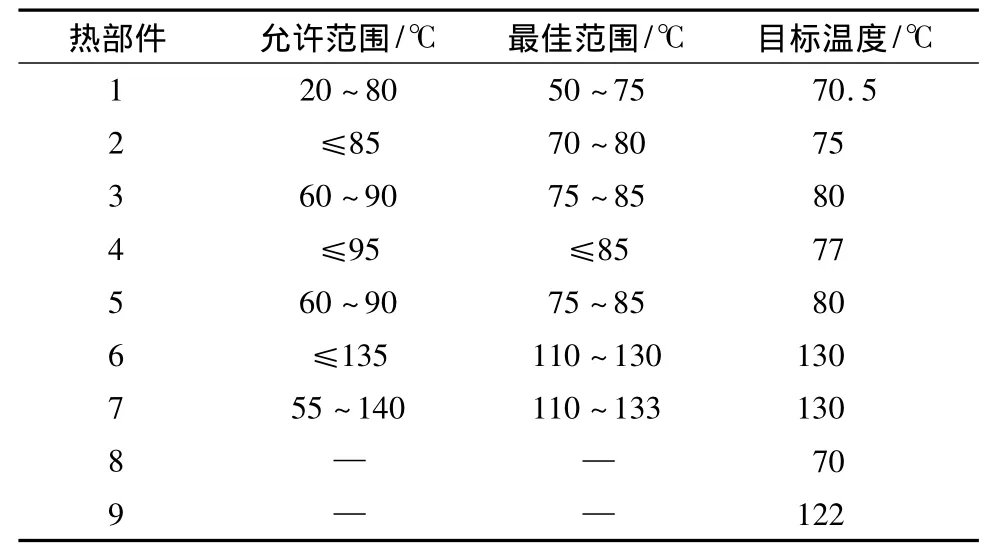
表1 热部件的工作温度范围
2.2 目标函数标准化
冷却系统能力的设计通常以额定工况点为设计点,同时以最大负荷点位设计校核点。设计时,在额定工况下,空气流量为qa0,此时冷却系统中各个热部件均在其目标温度点工作,由此可获得该数学规划问题的初始条件。对于多目标规划问题,通过事先确定目标之间的相对重要程度,然后采用加权平均等算法将多目标问题转换为单目标问题进行求解,是目前应用最广泛的方法[6]。

通过上述过程,发动机出口水温目标函数f'7(x,t)的允许范围为[-2,2],最佳范围为[-1,1]。依照此法获得其余目标函数f'i(x,t)。
2.3 加权系数
加权系数通常由决策者根据主观偏好、专家经验与数理分析等方式给出[7],并在仿真及后续试验过程中不断调整。该冷却系统中,柴油机本体出口水温为冷却系统的重要观测点,反映柴油机本体的热状况;机油及传动油温度反映了机械摩擦面的冷却润滑情况,是确定柴油机起动时机和装甲车辆行驶工况的重要参考;中冷器后冷却液温度反映柴油机进气情况(进气影响柴油机性能,但通常不影响安全性、可靠性);电机出口冷却温度反映电机热状况,其上限比下限更为重要;电池冷却器出口水温反映电池冷却情况,其散热量较小,且总路流量较大(热容大),因此进出口温差变化不大。根据冷却系统结构原理及各个热部件的重要程度、受温度影响的敏感度和温度目标范围等确定了各目标函数的加权系数,如表2所示。

表2 各目标函数的加权系数
因此,该多目标规划问题可以转化为单目标问题:
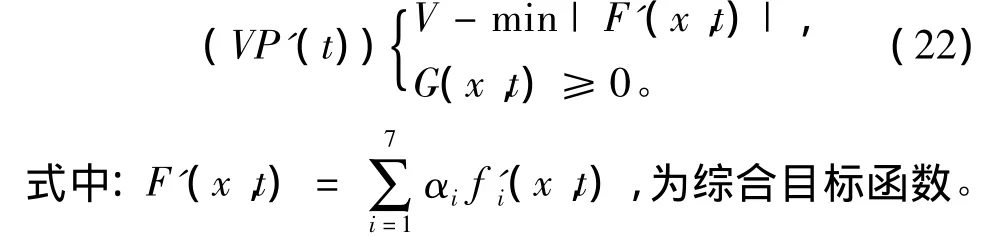
3 仿真与分析
随着计算机技术的发展,数值仿真成为单变量多目标数学规划问题求解的重要手段。笔者根据冷却系统结构原理,在一维传热仿真环境中建立冷却系统数值模型,在Simulink中建立单变量多目标数学求解模型,二者耦合仿真进行求解。
3.1 冷却系统数值模型
数值模型建立的准确性直接关系到计算结果的准确程度。冷却系统数值模型中的部件模型主要有:热源部件、换热器(包含散热器)、水泵、膨胀水箱、风扇、风道与管道等。
1)热源部件
热源部件建模主要考虑其散热量、冷却液流量、阻力及冷却水腔体积等流动与传热参数,如表3所示。
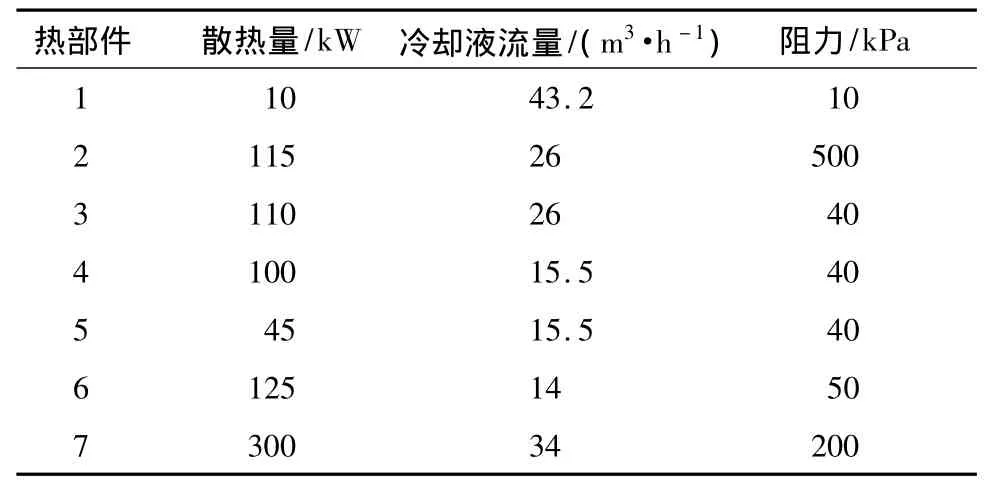
表3 额定工况下各热源部件流动与传热参数
2)换热器
换热器的模拟计算考虑了传热壁的热容量。通过散热片和两流体之间的热平衡来计算温度[8]:
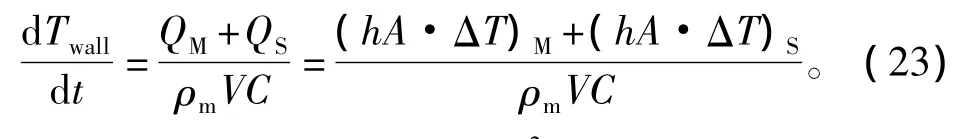
式中:h为传热系数(W/(m2·K));A为传热面积(m2);ΔT为流体和管壁的温差(K);ρm为散热片材料的密度(kg/m3);V为散热片材料的体积(m3);C为散热片的比定压热容(J/(kg·K))。
流体和散热片之间的传热率通过传热系数来表征,传热系数通过下列Nusselt关联式得到[9]:
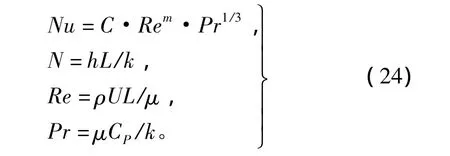
式中:L为特征长度(m);k为热传导率(W/(m·K));ρ为流体密度(kg/m3);CP为流体的比定压热容(J/(kg·K));U为流体流速(m/s);μ为流体的流动黏度(kg/(m·s))。
3)水泵与风扇
水泵与风扇的特性曲线相似,通过“扬程(压头)-流量(风量)”曲线定义[9]:
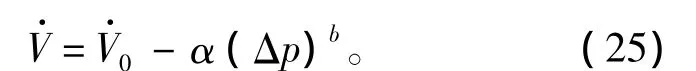
图3为所建立的冷却系统流动与传热数值模型。模型环境条件按设计要求设定温度为35℃,压强为100 kPa。
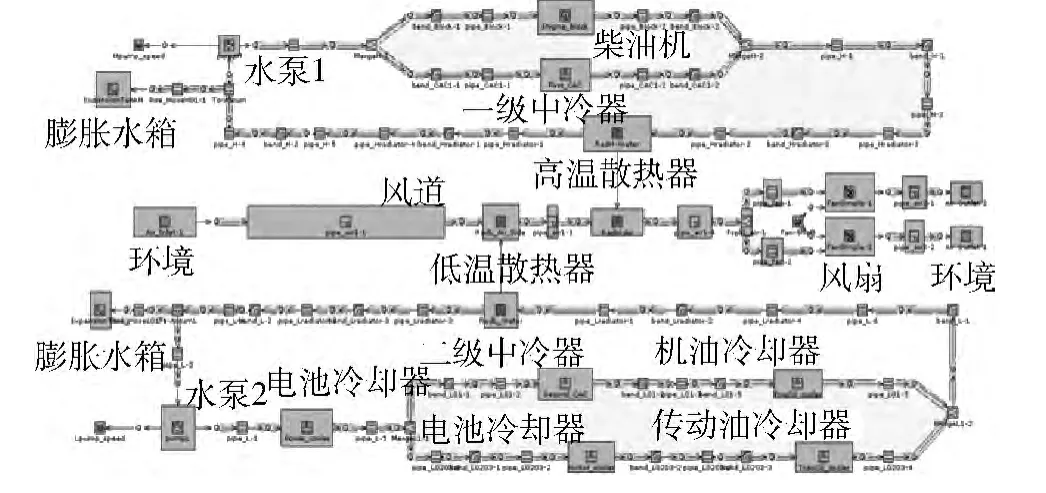
图3 冷却系统流动与传热数值模型
3.2 控制系统模型
结合冷却系统具有较大延迟、难以建立精确数学模型的特点,在控制时引入了模糊控制算法。图4为控制系统原理图,模糊控制器以单变量多目标数学规划的综合目标函数值及其差分为输入,以风量调节量(风扇转速)为输出进行控制。风量的基准量由冷却系统总传热量和环境温度等因素预先计算确定。同时,为保证风扇转速调整的稳定性,设定转速调整间隔为20 r/min。
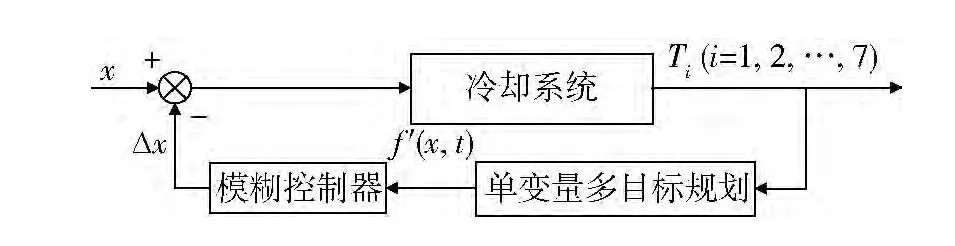
图4 控制系统原理图
基于Simulink建立了控制系统模型。图5为目标函数标准化模型,图6为控制系统模型。模糊控制器采用高斯型隶属度函数输入和三角形隶属度函数输出,其曲面观测图如图7所示(e、ec为模糊控制输入,u为输出)。
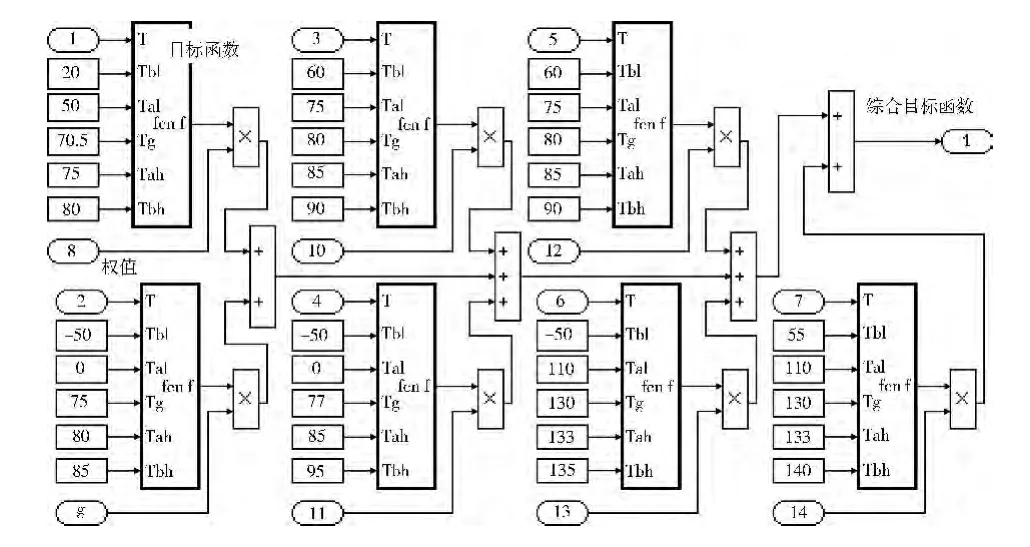
图5目标函数标准化模型
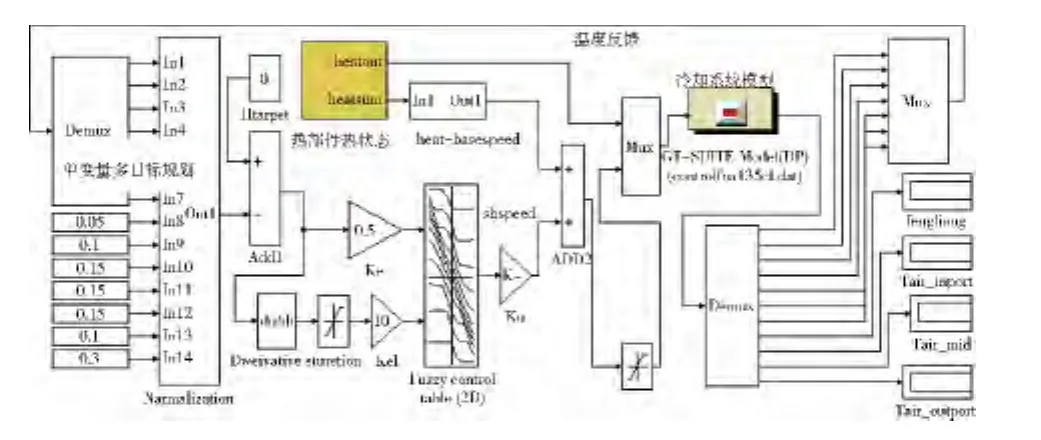
图6 控制系统模型

图7 模糊控制器曲面观测图
3.3 耦合仿真求解
3.3.1 基准转速函数
仿真前通过设置多个工况进行仿真,得到系统风扇基准转速与总散热量的关系,如图8所示。根据图8中数据拟合得到基准转速函数:
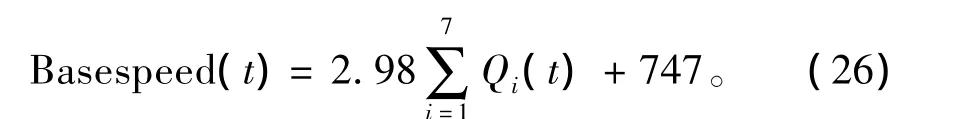
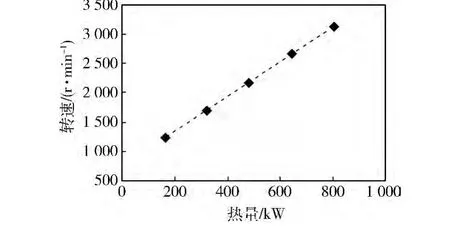
图8 总散热量与风扇基准转速关系曲线
3.3.2 工况设定
结合车辆实际运行状况,系统仿真时考虑稳定工况和过渡工况下的冷却系统运行情况。其中稳定工况设定点如表4所示,包含有快速行驶和低速大扭矩工况。稳定工况系统中各个热部件与冷却液的初始温度为环境温度,起车后以稳定工况运行。

表4 车辆稳定工况
过渡工况设定点如表5所示,包含有散热量降低和散热量升高的过渡工况。过渡时系统中各个热部件与冷却液的初始温度为前一工况下的温度,过渡后进入另一稳定工况。

表5 车辆过渡工况
3.3.3 仿真结果分析
根据设定工况进行仿真,得到冷却系统在基于单变量多目标数学规划及模糊算法控制下的运行状态参数。图9为稳定工况1中各观测点冷却液出口温度随时间变化曲线,可见:各个热部件的观测点冷却液出口温度都在目标温度范围内变化。在稳定工况1中,7个热部件观测点的综合目标函数值及风扇转速的变化曲线如图10所示,可以看出:风扇转速随着目标函数的变化而变化,其调节过程平稳、调节速度较快。图11-13给出了稳定工况2-4下的风扇转速与综合目标函数值的变化情况,可以看出其控制效果与工况1情况一致。
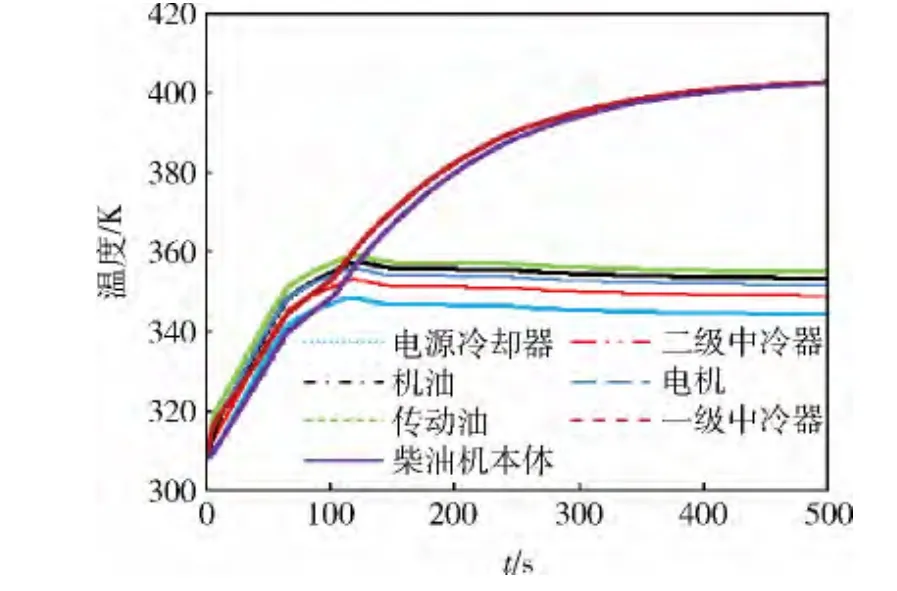
图9 稳定工况1中各观测点冷却液出口温度随时间变化曲线

图10 稳定工况1综合目标函数值与风扇转速变化曲线

图11 稳定工况2综合目标函数值与风扇转速变化曲线
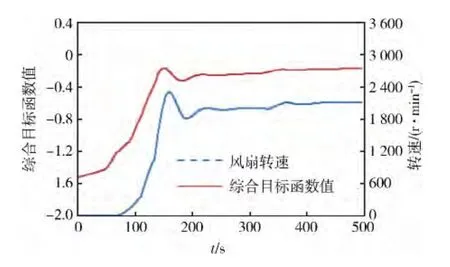
图12 稳定工况3综合目标函数值与风扇转速变化曲线
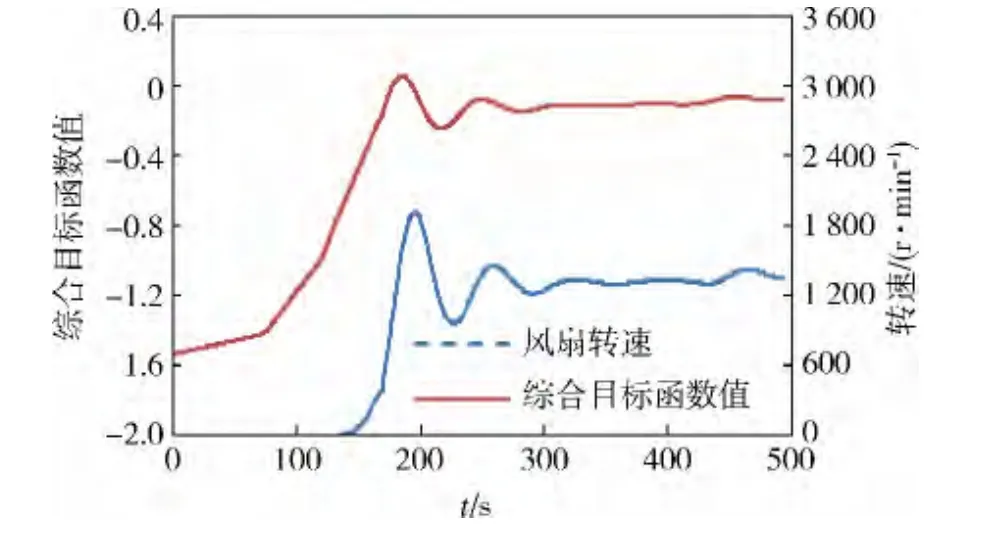
图13 稳定工况4综合目标函数值与风扇转速变化曲线
图14为过渡工况1中各观测点冷却液出口温度随时间变化曲线。可见:在车辆工况发生变化时,各观测点冷却液出口温度变化在目标温度范围内,其中加权系数最大的发动机出口水温最接近其目标温度。
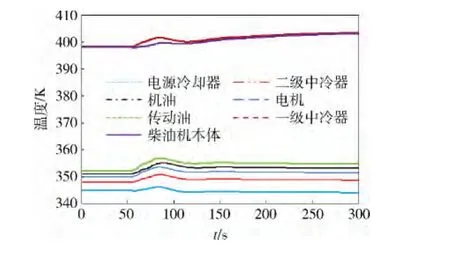
图14 过渡工况1中各观测点冷却液出口温度随时间变化曲线
图15为过渡工况1综合目标函数值与风扇转速变化曲线。可见:风扇转速随综合目标函数值的变化而变化,其调节过程响应速度较快。图16-18给出了过渡工况2-4的风扇转速随综合目标函数值的变化情况,可见:在工况变化过程中,综合目标函数值有较大幅度的变化,约1 min后恢复平稳。

图15 过渡工况1综合目标函数值与风扇转速变化曲线
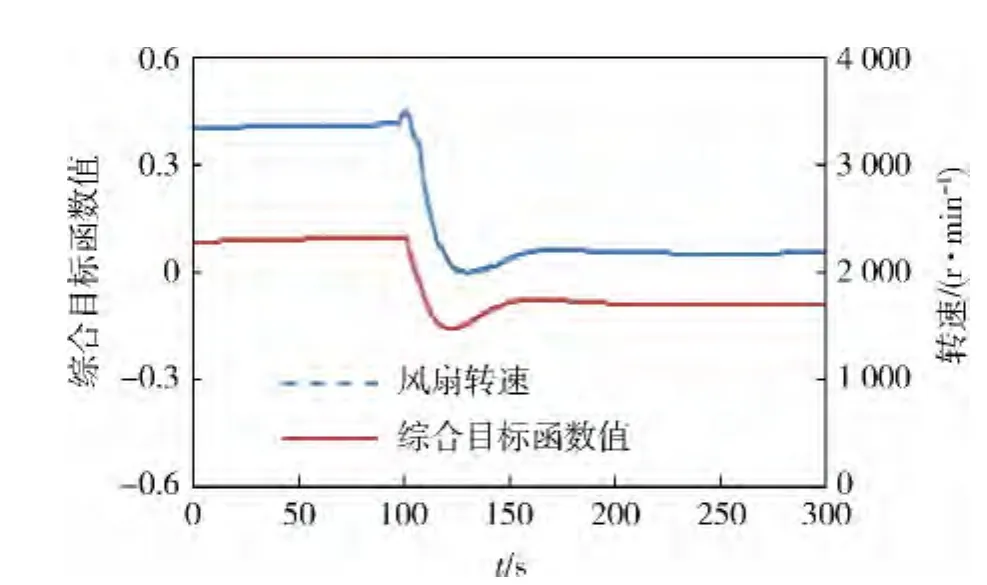
图16 过渡工况2综合目标函数值与风扇转速变化曲线
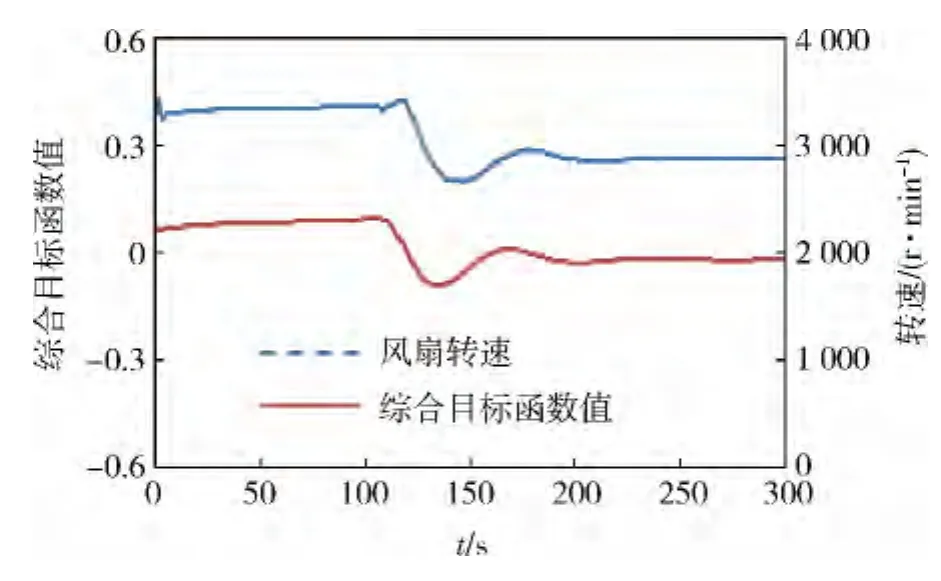
图17 过渡工况3综合目标函数值与风扇转速变化曲线
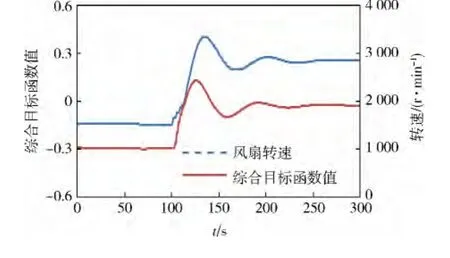
图18 过渡工况4综合目标函数值与风扇转速变化曲线
4 结论
针对新型装甲车推进系统中热部件多、散热量大、目标温度范围广而可调参数单一的问题,提出一种将单变量多目标数学规划与模糊智能控制相结合的控制算法。基于冷却系统流动与传热原理建立了冷却系统模型、单变量多目标数学规划模型及模糊控制器模型,研究了冷却系统在推进系统不同工况下的工作情况。结果表明:该控制算法具有良好的控制效果,能够有效地解决新型推进系统的单变量多目标控制问题,对新一代装甲车辆推进系统的研制有一定理论意义和参考价值。
[1] 郭新民,邢娟,高平.载重汽车发动机自控电动冷却风扇的研究[J].农机化研究,1997,2(1):31-33.
[2] 李启堂,徐继涛,丁书斌,等.基于改进PID的发动机冷却系智能控制系统的研究[J].机电一体化,2007(2):43-46.
[3] 骆清国,桂勇.装甲车辆发动机智能化控制冷却系统发展[J].装甲兵工程学院学报,2011,25(4):25-29
[4] 孙逢春,张承宁.装甲车辆混合动力电传动技术[M].北京:国防工业出版社,2008:148.
[5] 魏权龄,应玖茜.单变量多目标数学规划解的性质与解法[J].应用数学学报,1980,3(4):382-388.
[6] 乔伊科奇A,汉森D R,达科斯丁L.多目标决策分析及其在工程和经济中的应用[M].王寅初,译.北京:航空工业出版社,1987:209.
[7] 叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006:51.
[8] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,1998:106.
[9] 姚仲鹏,王新国.车辆冷却传热[M].北京:北京理工大学出版社,2007:23.

