基于NSGA－II算法的客运专线开行方案优化设计

裴金漪

（兰州交通大学 交通运输学院，甘肃 兰州730070）

1 模型建立

1.1 符号定义

设客运专线网路G＝｛S，E，C｝，其中S为车站集合，S中有N个车站。物理路网边集合E＝｛emn｜m，n∈S｝，每条物理路网边的实际通过能力C＝｛cmn｜m，n∈E｝。车站m和n之间运行线的开行方案可以表示为lmn＝｛ρmn，μmn，vmn，fmn｝，其中ρmn为该运行线的停站方案，μmn为旅客列车类型，vmn为旅客列车的开行速度，fmn∈N为开行频率。因此，关于客运专线网路G的开行方案可以表示成为L＝｛lmn｜m，n∈S｝。

设车站m，n之间的可能运行线路为εk∈ρmn，其中ρmn为m，n之间可能运行线的条数。为了便于分析讨论，假设乘客全部偏向于选择最近的道路出行。在此基础上所有的开行方案都应尽量满足任意m，n间的旅客出行需求，即没有换乘的情况。采用Dijstra算法在已知客运专线网路G上搜寻m，n之间的最短开行路线，将εmn∈ρmn作为m，n之间的开行线。因此，lmn＝｛εmn，μmn，vmn，fmn｝可以用来表示经过Dijstra算法搜索后的开行方案。

设m，n之间开行列车的动车组数和车厢的编成量数分别为K1，mn和K2，mn。Amn为车厢定员，每节车动车组或机车的固定和变动费用为U1，mn和U2，mn，每节车厢的固定和变动费用为C1，mn和C2，mn。设每条运行线所需车底数为＾nmn＝（fmn＾tmn／T），其中＾tmn为运行线lmn的估计周转时间，T为路网G的运行周期。

图1 支配解和Pareto边界

设nodesmn为运行线lmn上的停站数目，tmn为停站时间，˜tmn为等待时间，停站时间、等待时间和运价率与开行速度和旅客列车类型相关。当该运行线上的列车类型和开行速度确定后，nodesmn，tmn和˜tmn皆为常量。

1.2 目标函数

根据以上的符号定义，极小化铁路部门运营总成本可表示为

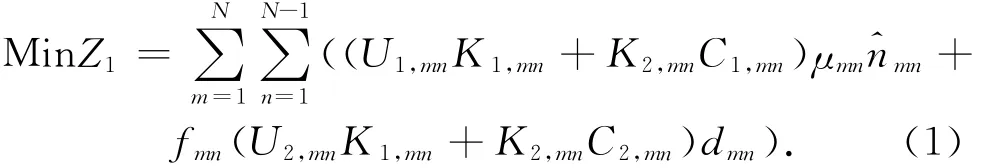
式中:dmn为m，n间的开行距离。

极小化系统的旅客票价总成本为

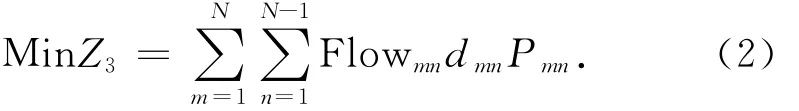
式中:Flowmn为实际客流量，Pmn为该运行线上的运价率。

极小化旅客旅行总时间为

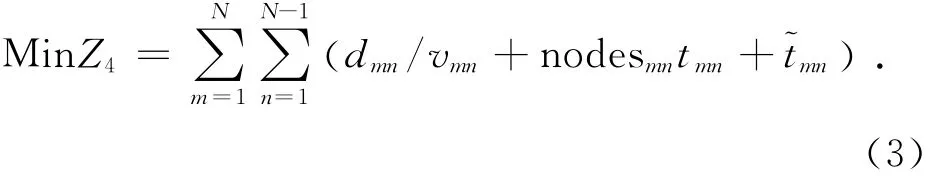
为了让算法得到更好的收敛性值，我们对目标函数进行标准化，则有公式

式中:k＝1，2，3；Scalek＝max（Zkj）N（N－1），为目标函数的标准化参数。

1.3 约束条件

物理路网边上的开行频率之和小于该路网边的实际通过能力

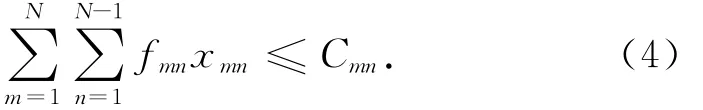
式中:xmn为决策变量，当εmn通过物理路边emn时，xmn＝1，否则为0。

车站m，n之间的开行方案满足其间的客流量要求

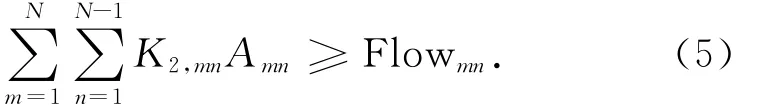
另外，在实际情况中，一条运行线只能开行一个频率的列车。该约束条件在遗传算法中会自动表达在”染色体”结构中，因此，无需额外写出。

2 NSGA－II算法的建立

2.1 Pareto边界及非支配解

在NSGA－II算法中，将所有由非支配（Nondominated）点组成的曲线称为Pareto边界。在图1中，对于点2来说，点3在两个极小化目标上均优于点2，因此，点2被点3支配。Pareto边界上的点由极小化铁道公司总成本和极小化旅客旅行总成本构成，是一种多目标函数优化问题，Pareto边界上的点代表了在某一妥协方案（通过权重系数将多目标优化转化为单目标优化）下的开行方案。也就是说如果得到了Pareto边界，便得到了所有可能的“最优解”。

2.2 Dijstra最短路径算法

在进行开行方案的设计之前，首先要确定任意两个车站间的开行路线。假设所有旅客都选择最短的路径出行，采用Dijstra算法在已知路网G上搜寻任意两车站所对应的最短路径，其具体做法为:

1）首先根据G确定车站之间的距离矩阵D，D为N×N的对称矩阵，在D中将实际相连（即emn存在）的距离记为实际距离，将实际不直接相连的车站间距离记为正无穷（Infinity）；

2）利用Dijstra算法更新D中的值直到所有的站间距离d＝Infinity，当找到了所有车站对的最短开行路径后，ρmn也就能够确定了。

2.3 遗传算法设计

染色体采用二进制编码，分为开行频率f和开行等级μ两部分，分别采用二进制编码。对于开行频率子串:每条运行线对应唯一的开行频率，假设开行频率取fi∈［0，F］，i＝1，2，3，…，N（N－1）。其中F∈N（F为自然数）表示开行频率的上限，N为车站数。因此，为了表述每条运行线开行频率所需的二进制数为Binf＝ln（F＋1）／ln（2）。开行频率子串的长度可以表述为N（N－1）·Binf。对于开行等级字串，开行等级不仅对应着开行列车类型μ，还包括开行速度v，停站时间t等信息。设一共有Nμ种列车类型，每种类型对应的开行速度一共有Nv种（由于开行速度确定后停站时间、等待时间等信息也会自动确定，所以，只需要确定开行速度即可），因此，表述每条运行线所需要的二进制数为Binv＝ln（NμNv＋1）／ln（2），开行等级子串的长度为N（N－1）·Binv，染色体的结构如图2所示。开行等级矩阵V中存储着不同类型的列车开行速度、等待时间、停站时间等信息，当染色体随机生成后，可通过二进制转换成十进制来检索矩阵V中的信息，并将其换算成需要的列车信息。

图2 染色体结构示意图

NSGA－II算法的具体流程如图3所示，当种群数量为P的染色体生成后，需要进行交叉变异来生成新的数量为P的种群。交叉和变异均在每一运行线染色体段上单独进行，交叉概率为80%，编译概率取10%。将进行过交叉变异的P个个体和原始的P个个体结合成种群数量为2P的种群Q，下一步需要确定2P个个体的非支配等级（Non－dominated level），以便于进行非支配等级划分。

非支配等级的确定可以通过下述方法确定:在种群Q中确定所有非支配个体，并将这些个体标记为level 0；在剩下的所有个体中确定非支配个体，将其标记为level 1；如此重复直到所有个体都含有level标记；如果某一个体不满足约束条件，该个体的非支配等级levelk＝levelk＋levelmax＋1，其中levelk为该个体未进行约束分析时的非支配等级。

当Q中所有个体的非支配等级确定后，为使最后的解相对均匀地分布在所需要的Pareto边界上，需要确定每一个非支配等级下个体的拥挤等级（Crowding distance）。设个体i－1，i和i＋1的非支配等级相同，为，且k＝i－1，i，i＋1为三个个体标准化后的目标函数值，则个体i的拥挤距离为

利用非支配等级和拥挤距离可进行选择操作，选择进行下一代遗传变异操作的个体。具体做法为:将Q中的所有个体按照非支配等级从低向高排列；选出非支配等级小于k的所有个体，且k应满足小于等级k的个体数都小于P，小于等级k＋1的个体数都大于P；计算非支配等级k中所有个体的拥挤距离，并按照从大到小排列；在Q中选出前P个个体作为新的亲代个体。

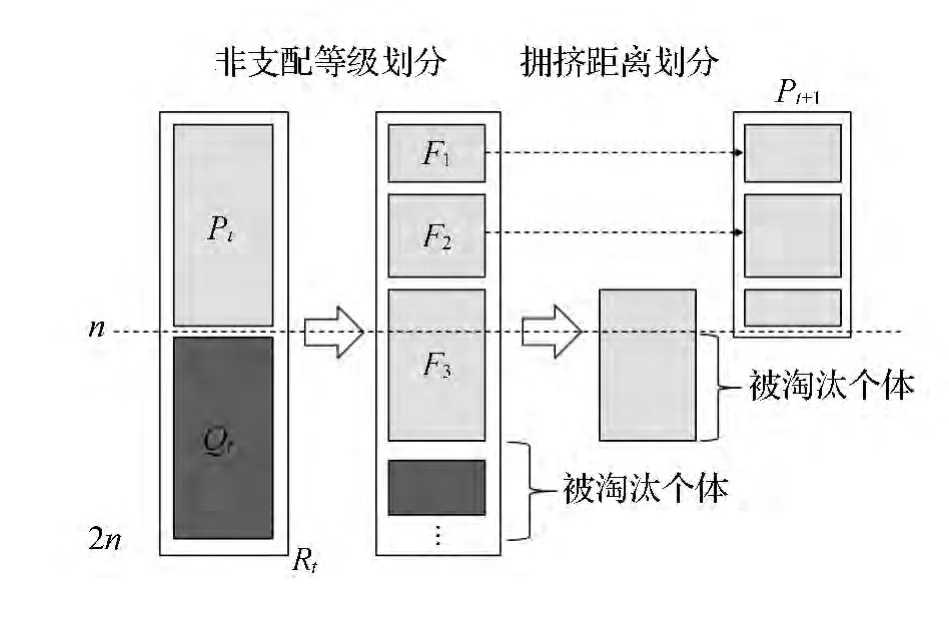
图3 NSGA－II算法流程示意图

3 算例分析

为验证以上理论的正确性，构建简单的铁路客运专线路网模型，利用MATLAB进行数值模拟、路网模型及相关数据参考。图4为客运专线路网示意图，物理路网边上的信息为站间距离和路边实际运行能力。旅客旅行总成本的加权因子β＝0.5，运行周期T＝60min。遗传算法的个体数P为300，运行代数为50代。表1为运用算法优化后得到的最优运行线。

图4 客运专线路网模型

表1 开行路线表

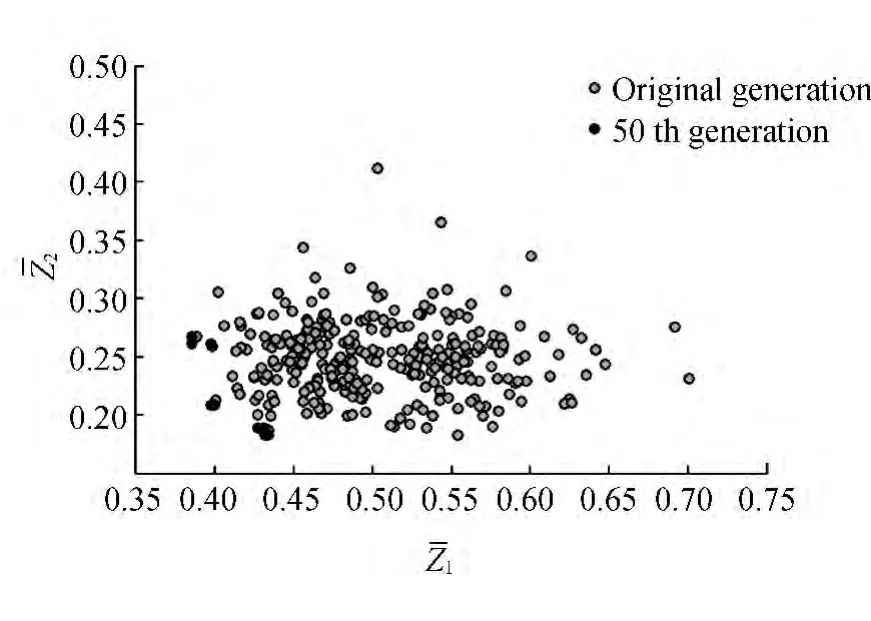
图5 第50代种群与初始种群分布

图6 为第50代个体分布示意图，从图6中可以看到大部分个体已经发生重合并且分布在大致三个区域（如虚线圆形区域所示）。暂且将这三个区域按照升序，称为类别一，类别二和类别三（见表2，表3，表4）。分别在三种类别中挑选出非支配等级最低的个体作为代表来分析三类解的特点。

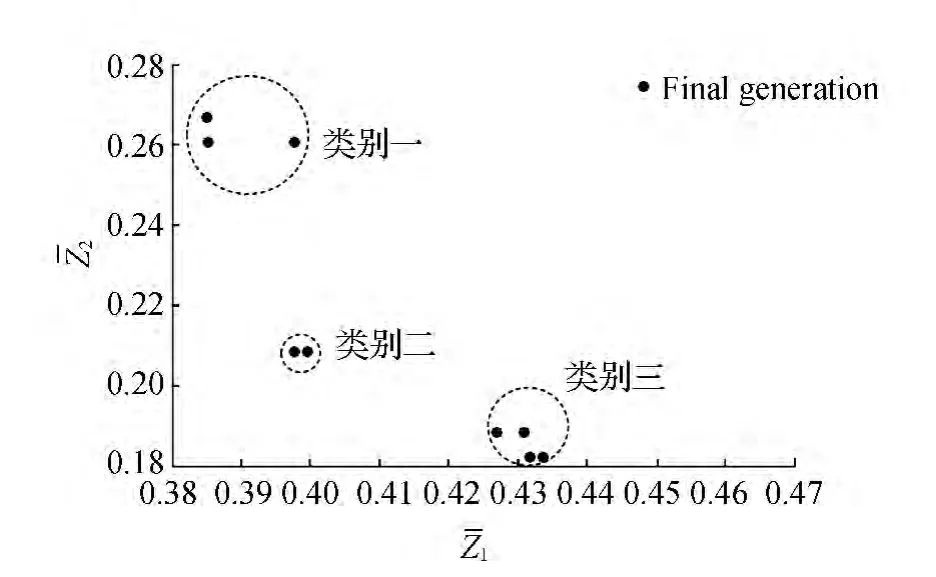
图6 第50代种群分布类别示意图

表2 类别一开行方案

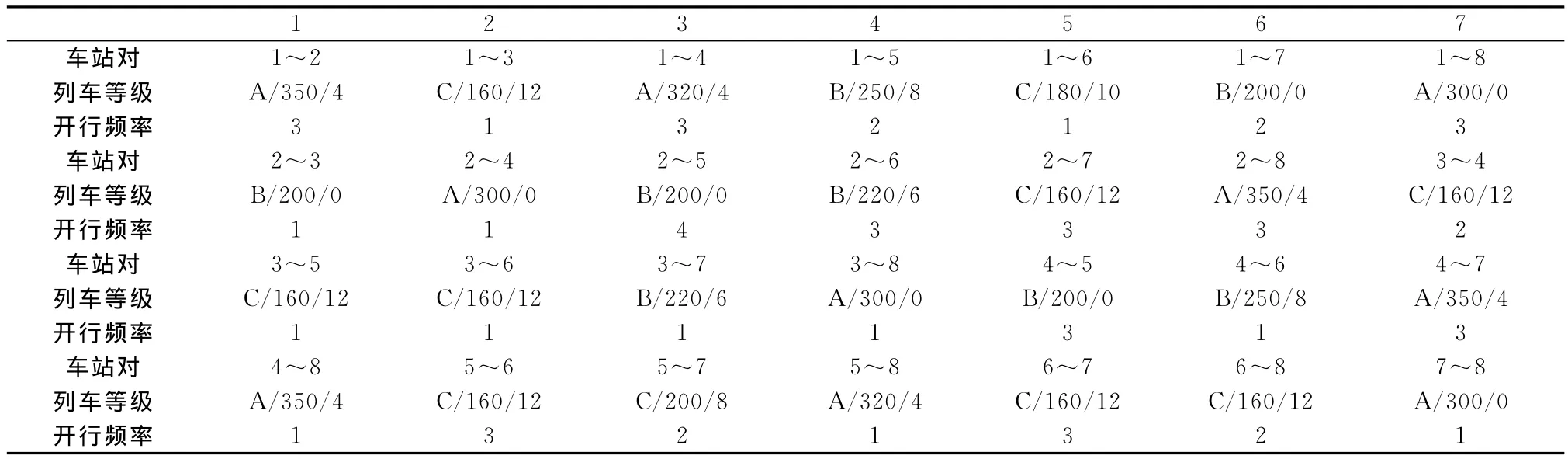
表3 类别二开行方案

表4 类别三开行方案

表2～表4分别列出了三类开行方案，表5给出了三类解情况下目标函数的对比值。通过分析所得数据可以发现一类解对应的铁路公司开行总成本最低，在一类解下B类、C类列车站的比重较大（15／28），这种情况下相应的旅客出行票价成本和时间成本也较高，对旅客的出行带来很大的不便。这类解可以运用在客流量大、客运压力大的情况下，同时，铁路公司运营欠佳时也可以采用。第三类解的情况与之相反，铁路公司收入最少，乘客的旅行成本最低，这种情况可以看作是乘客出行要求较高的情形，例如春运期间需要最大限度地降低旅客出行成本的情况。相对于类别一和类别三，类别二属于较为中和的方案，适用于一般、无特殊事件情况下的开行方案。

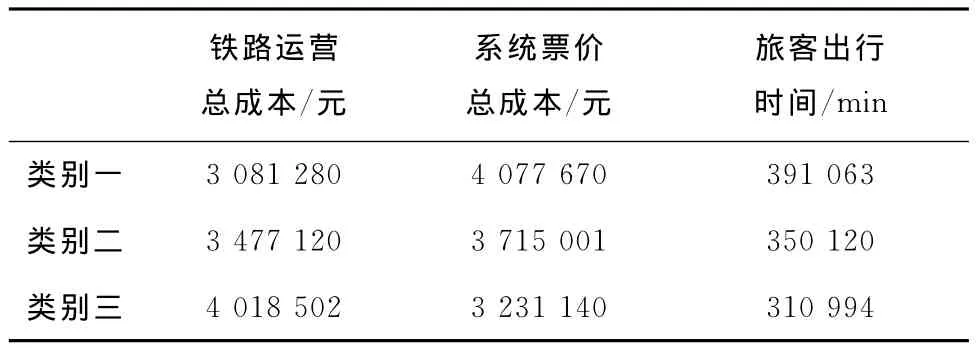
表5 三类解目标函数值对照表

4 结束语

首先利用Dijstra最短路径搜寻算法在已知客运专线路网上搜寻最短开行路径。然后在确定的开行线路上运用NSGA－II多目标优化算法进行开行方案的优化。对开行方案的“染色体”编码采用两段式，并对其分别进行了交叉操作和变易操作。最后，对得到的优化结果进行分类处理，并讨论了三类解在实际问题中的意义。该方法并不能将Dijstra算法运用在迭代循环中，实验证明这种尝试是不收敛的，所以，本文并不能根据实际的开行结果选择最短路径。下一步的研究工作就是尝试如何将选线方案与开行方案进行联合优化，将Dijstra算法整合到迭代循环中。

［1］牛惠民，陈明明，张明辉.城市轨道交通列车开行方案的优 化 理 论 及 方 法 ［J］.中 国 铁 道 科 学，2011，32（4）:128－133.

［2］邓连波，史峰.旅客列车开行方案评价指标体系［J］.中国铁道科学，2006，27（3）:106－110.

［3］Bussieck，M.R.，P.Kreuzer，and U.T.Zimmermann，Optimal lines for railway systems［J］.European Journal of Operational Research，1997，96（1）:54－63.

［4］Dijkstra，E.W.，A note on two problems in connexion with graphs［J］.Numerische mathematik，1959，1（1）:269－271.

［5］Deb，K.，et al.，A fast and elitist multiobjective genetic algorithm:NSGA－II［J］.Evolutionary Computation，IEEE Transactions on，2002，6（2）:182－197.

［6］李引珍，何瑞春，郭耀煌，等.多目标网络相异路径的Pareto解及其遗传算法［J］.系统工程学报，2008，28（3）:264－268.

［7］贾晓秋，关晓宇.客运专线网络列车开行方案模型与算法研究［J］.系统工程学报，2011，26（2）:216－221.

［8］曾玮，王佟.基于列车时刻表的城际铁路客流分配研究［J］.交通科技与经济，2014，16（2）:24－26.