出租车行业规制与放松规制分析

蒋晶尧，王利利，刘玉露

（1.玉林市城乡规划设计院，广西 玉林537000；2.西南交通大学 交通运输与物流学院，四川 成都610031；3.湖北省交通运输厅随岳高速公路管理处，湖北 武汉430050）

长期以来我国出租车行业一直处于严格的规制状态，因此，很多人将出租车行业中存在的许多问题归咎于严格的行业规制。近年来，社会各界对于出租车行业规制的争议和质疑越来越多，要求出租车行业放松规制甚至是完全解除规制的呼声也越来越高。规制是指在市场经济体制下，政府为了矫正和改善市场内在问题而对经济主体活动进行的行为。放松规制是自然垄断行业规制改革的重要趋势，是指放松或者取消众多规制政策中的一部分或者全部。出租车行业放松规制的实质是重新调整政府与行业的关系，通过引入竞争、政策调整等方式，进一步提高服务质量，降低收费水平，提高经济效益，改善社会福利。

国外的出租车规制主要涉及出租车数量、费率、服务和安全标准等方面。国外学术界较早就开始了对出租车行业的规制研究，并在不同的时代侧重于不同的方面。20世纪70年代的文献集中讨论了出租车巡游服务市场价格竞争的可行性。20世纪80年代的研究开始区分出租车服务市场的内部结构，分别讨论不同市场的特征和竞争条件。进入20世纪90年代后，放松出租车规制的实践陆续在一些发达国家出现，对出租车规制的研究，在之前的研究基础上，进一步深入和细化。Moore和Ted Balaker分析比较了28篇1980～2005年出租车放松规制方面的文献，发现其中19篇（占68%）支持放松规制，7篇（占25%）反对放松规制，2篇（占7%）持折中观点。随着众多地区对出租车行业的放松规制实践和出租车行业规制研究的深入，国外研究出租车行业规制的学者中，大部分已经认同出租车行业应该放松规制。我国的王军对十几个国家和城市的出租车行业规制变革进行了研究，对比我国出租车行业的现状和问题，对我国出租车行业规制提出放松数量管制，实行最高费率制或费率备案制，提出建立必要的、最低限度的安全和服务标准管制的建议。

近年来，随着我国的交通快速发展，伴随着该行业的不断发展，出租车规制问题也得到重视。游保德、程金亮从政府规制的角度出发对出租车经营模式进行了分析，并提出相应的对策建议。徐飞、郭爽从准入、价格、数量和服务质量规制四个角度出发对沈阳市出租车行业现状进行分析，并提出改善策略。邵燕斐、王小斌使用两方博弈模型探讨出租车提价能否有效增加司机收入与社会福利。章亮亮从经济学与行政法学分析了出租车需要竞争才能健康发展。

1 出租车行业无规制条件下的社会福利分析

在无规制的条件下，出租车行业内各出租车公司进行自由竞争。假设行业内只有两家出租车公司，分别为公司1和公司2。由于规模经济效应，两家公司会展开竞争来扩大规模提高收益。两家出租车公司的运营目标都是获得最大的经济收益。假设两家出租车公司的成本函数和利润函数都是不同的，但面对相同的市场，即需求函数相同。这是一个典型的库诺特（Cournot）竞争，可以利用博弈论中的库诺特竞争模型来进行分析。

用q1，q2分别代表两家出租车公司在市场中的服务供给量，服务供给量用出租车营运里程公里表示。用C1，C2分别表示两家出租车公司的成本，成本函数可以分别表示为C1（q1），C2（q2）。消费者对出租车服务的需求函数可以表示为Q＝Q（p，f），其中p为价格，f为服务质量。

由于出租车的服务质量受到出租车司机的服务态度、道路情况、乘车时间等多种因素影响，而且出租车服务多为巡游服务，具有一次性和随机性的特点，因而，需求对其服务质量敏感性较低。将需求函数简化改写成Q＝Q（p），市场的需求函数为Q＝q1＋q2＝Q（p），逆需求函数为P＝P（q1＋q2）。

两家出租车公司的利润函数分别表示为

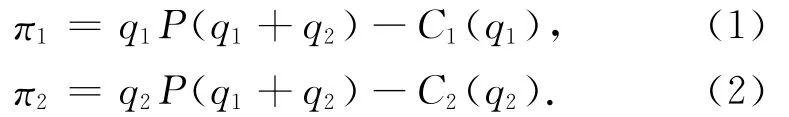
令（q＊1，q＊2）为两家公司各自经济收益最大化时均衡状态下的运营里程，则有

对每个公司的利润函数求一阶导数

这两个反应函数的交叉点即纳什均衡点q＊＝（q＊1，q＊2），如图1所示。

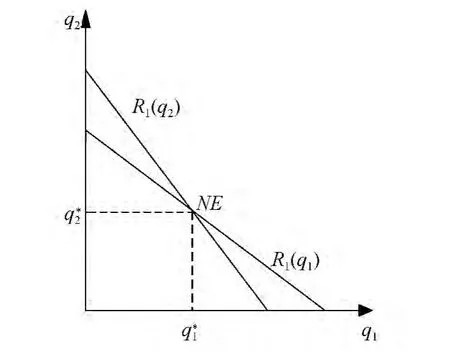
图1 库诺特模型的纳什均衡

为了进行更具体的分析，假定出租车公司的单位运营里程的平均成本分别为c1，c2，则出租车公司的成本函数可以表示为C1＝c1q1，C2＝c2q2；逆需求函数取P＝a－b（q1＋q2）的线性形式，那么，可解得最优条件下的均衡解为

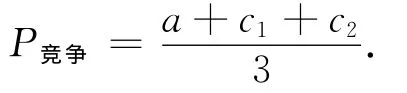
当c1＜c2时，q＊1＞q＊2。经过上面的分析，可以确定无规制条件下，出租车市场上更多的市场份额会由单位平均成本较小的一家公司获得。

如果两家公司均处于规模经济水平，由于过度竞争会致使公司自身利益受损，二者不会发生恶性竞争。但如果其中一家公司没有达到规模经济，那么它为了追求最大化的收益就需要扩大市场份额，两家公司会重新分配出租车市场的市场份额。

假定只有公司1达到规模经济水平，那么，只要c1下降水平使得均衡价格，公司2就会由于无法获得任何收益而退出市场竞争，此时c1＜2c2－a，公司1将完全占据市场，获得垄断地位。公司1成为垄断企业后，其最大收益可以表示为 maxπ＝Q（a－bQ－c1）。

显然垄断状态下的价格要高于竞争状态下的价格，这会导致一部分消费者剩余转化到公司1中，另一部分则形成损失。而且提高的垄断价格会造成市场需求的降低，一些有需求的消费者无法享受乘坐出租车的福利，整体社会福利受损。

前面的分析并没有考虑出租车行业的负外部性。出租车行业存在负外部性，包括其使用过程中占用的道路资源、消耗的能源、污染环境的尾气排放等。传统经济学认为在纯粹竞争的市场机制条件下，社会边际收益（SMR）与个人边际收益（PMR）相等，社会边际成本（SMC）与个人边际成本（PMC）相等，见图2（a）。但是当考虑到负外部性时，社会边际成本会大于个人边际成本，其差额就是外部成本（EC），见图2（b）。如图2（b），在出租车行业中由于负外部性的存在，SMC曲线必然在PMC曲线上方，出租车公司为了实现自身利益最大化，按照边际成本与边际收益相等的原则决定其市场供给量S1和价格P1，在供给量为S1，PMC为AS1，而SMC为BS1，其差额BA就是EC。由于P1没有反映供给量为S1时的负外部性，从社会角度，P1的成本价格过低必然造成供给量过大，导致资源配置的低效率和社会福利的损失。因此，以社会效率和社会福利为出发点，如果不对出租车行业进行政府规制，市场的力量会导致资源配置的低效率，造成社会福利的损失。

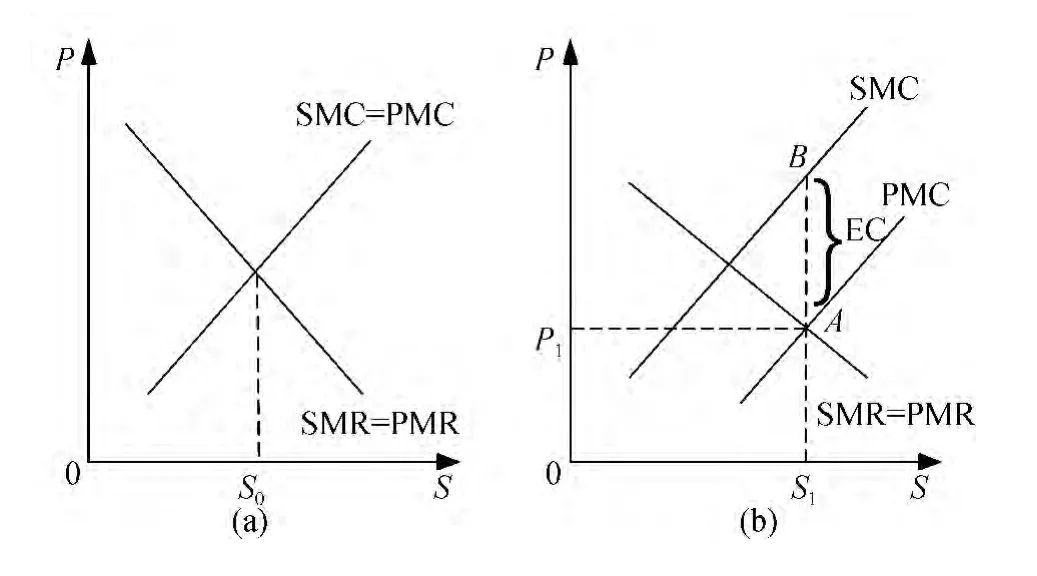
图2 社会边际效益与个人边际效益

2 出租车行业规制条件下的社会福利分析

出租车行业规制主要包括总量规制和价格规制，下面将从这两个方面来分析规制对出租车行业的社会福利影响。

2.1 总量规制下出租车行业的社会福利分析

出租车公司的利润函数为:πi＝Pqi－Ci（qi），i＝1，2，…，m。根据福利经济学相关理论，进行如下分析。出租车行业的剩余为消费者的剩

假定出租车行业规制只有总量规制来对行业内的出租车公司数量及公司规模进行限制，行业内所有出租车公司均能够达到规模经济状态，行业内出租车公司数量为m，每个出租车公司单位运营里程的平均成本为ci，i＝1，2，…，m。

出租车市场的逆需求函数为余为

社会总福利为行业剩余与消费者剩余之和，表示为

政府的总量规制条件下，要达到的目标为以下两点:

1）行业剩余最大化

2）社会总福利最大化

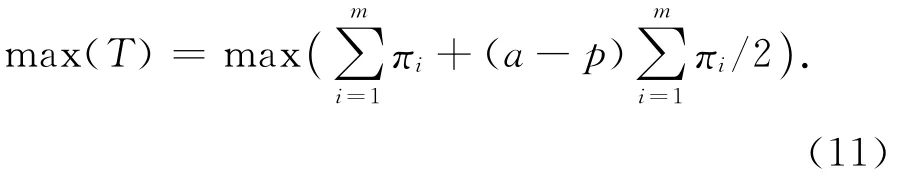
假设每个出租车公司的平均成本相等，即ci＝c，则社会总福利为

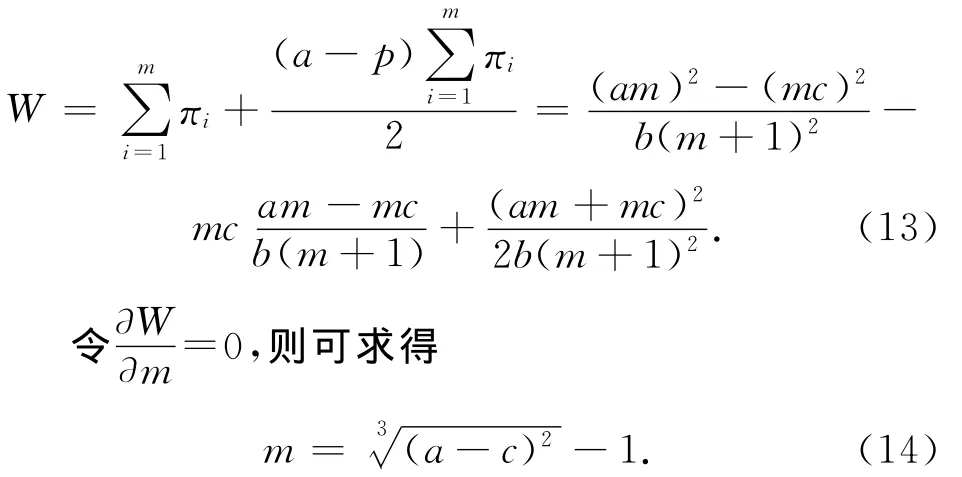
通过分析，总量规制下的行业内出租车公司数量与平均成本反相关，平均成本越小的公司在市场中的服务供给量越大，规模经济临界点决定了公司的规模。因此，可以通过总量规制实现每个公司的规模经济，而此时的社会福利能够得到改善，高于垄断竞争时社会福利。然而，如果价格仍然由市场决定，那么在获取更多垄断利润的驱动下，出租车公司的竞争行为最终仍然会走向垄断，市场的价格会重新上升到垄断水平，从而导致规制失灵，最终社会福利仍然不能得到改善。因此，单一的总量规制并不能提高社会福利，必须考虑价格规制的作用。

2.2 价格规制下出租车行业的社会福利分析

政府对出租车行业的规制中，对价格进行限定，这样市场内的出租车公司就无法把价格提高到更高，也不存在动力来获取垄断利润。假定行业内只有一家出租车公司，在政府不实施价格规制时，其利润函数为π＝PQ－cQ，逆需求的函数为P＝a－bQ。此时的社会总福利为。出量，令，则可得到社会总福利最大化的条件为租车公司会按个人利润最大化来决定其服务供给

在政府实施价格规制的条件下，假定政府的定价为P′，此时公司的利润函数为π′＝P′Q′－cQ′。社会福利为根据社会福利最大化的原则（Maxπ′，MaxW′），可以解得P′＝c，

此时社会总福利为

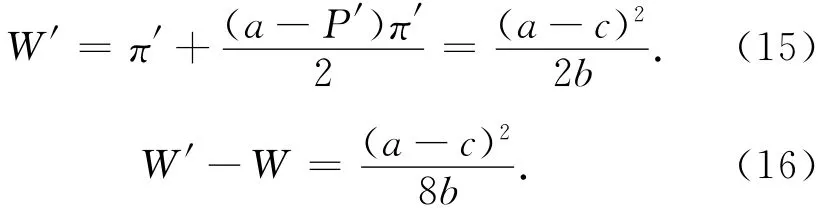
相比未实施价格规制时的社会福利，此时的社会福利明显地得到了提高，从而说明政府对出租车行业的价格规制能够实现资源的有效配置，对社会福利起到改善作用。还可以发现，进行价格规制和同时进行总量和价格规制对社会福利的影响效果是相同的，从社会福利角度来看，总量规制是没有必要的。

通过以上分析，可以发现出租车行业规制条件下的社会福利与无规制条件下的社会福利相比，明显得到了改善和提高。从社会福利角度来看，政府对出租车行业进行规制是有效的，能够规避行业发展中的垄断，解决资源配置低效率、负外部性等问题。

3 放松规制条件下的社会福利分析

前面分析了出租车行业无规制条件和规制条件下的社会福利，下面将分析出租车行业放松规制条件下的社会福利。模型假设:

1）假设出租车行业原有公司的营运里程为q0，放松规制后，由于竞争以及准入条件的改变，原有市场中有z（z＝1，2，…，z）个新公司进入行业，假设其营运里程为qi，单位营运里程的平均成本均为ci；

2）考虑出租车行业的价格规制，假设各公司只能调整自己的营运里程，出租车市场的逆需求函数为

3）政府规制的目标是社会福利最大化，出租车公司的目标是公司利润最大化；

4）政府规制决定新进入行业的公司数量z，行业内原有出租车公司先决定营运里程q0，后进入的公司可观测到q0，然后选择自己的营运里程qi。

这是一个典型的斯坦克尔伯格竞争模型，可以利用博弈论中的斯坦克尔伯格竞争模型来进行分析。

出租车公司i的利润函数为

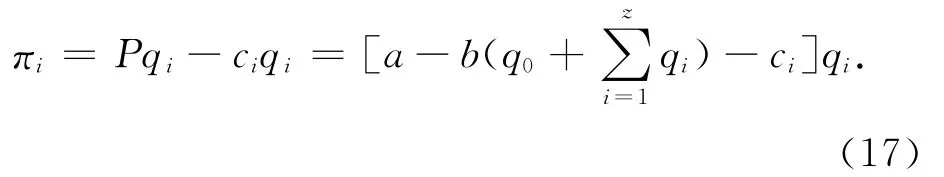
为求出租车公司i的利润最大化，令

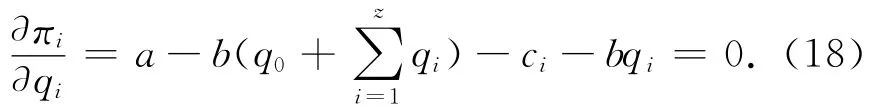
考虑到公司1，2，…，z之间的对称性，令q1＝q2＝…＝qz，c1＝c2＝…＝cz＝c，可解得可得

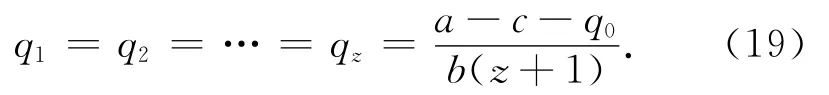
原有出租车公司的利润函数为

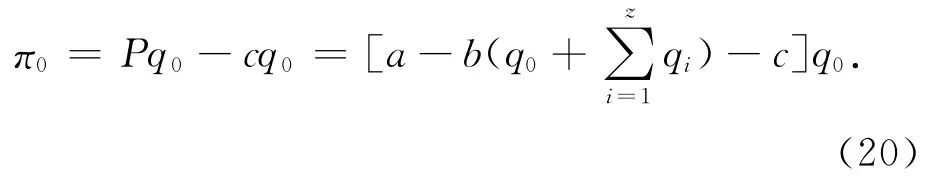
社会福利函数为

通过以上分析，可以发现放松规制后，进入出租车市场的出租车公司数量增加，社会福利会不断提高。这里我们分析的是在价格规制的条件下，出租车行业放松总量规制对社会福利的影响，显然在这一条件下，社会福利得到了改善。但如果在没有价格规制的情况下放松总量规制，出租车行业就会处于无规制状态，这时市场的过度竞争会导致资源配置的低效率，造成社会福利的损失。因此，对出租车行业放松规制，必须要考虑价格规制的作用。

4 结束语

对出租车行业不同规制条件下的社会福利和放松规制的影响进行分析，首先利用博弈论中的库诺特竞争模型对出租车行业无规制条件下和规制条件下的社会福利进行分析，分析过程中考虑了出租车行业的负外部性特征，结合了出租车行业的总量规制和价格规制。根据分析确定了出租车行业规制对社会福利的改善和提高作用，说明出租车行业规制的有效性。然后利用博弈论中的斯坦克尔伯格竞争模型分析了出租车行业放松规制后对社会福利和行业成本的影响，通过分析发现出租车行业放松规制后，社会福利会进一步得到改善和提高，而行业平均成本会有所降低，从而说明放松规制的必要性，因而，放松规制是出租车行业的规制发展方向。

［1］马云泽.规制经济学［M］.北京:经济管理出版社，2008.

［2］王春生.七台河市出租车行业政府管理对策［D］.哈尔滨:黑龙江大学，2006.

［3］陈富良.放松规制与强化规制［M］.上海:上海三联书店出版社，2001.

［4］Adriant Moore and Ted Balaker，Do Economists Reach a Conclusion on Taxi Deregulation ［J］.Econ Journal Watch，January 2006，3（1）:109－132.

［5］王军.为竞争而管制:出租车业管制改革国际比较［M］.北京:中国物资出版社，2009.

［6］游保德，程金亮.中国城市出租车市场经营模式［J］.当代经济，2014（5）:28－30.

［7］徐飞，郭爽.出租车行业规制问题研究:以沈阳市为例［J］.经济师，2013（11）:171－173.

［8］邵燕斐，王小斌.基于博弈论视角的出租车价格管制困境破解［J］.开放研究，2014（2）:139－143.

［9］章亮亮.对出租车行业特许模式的经济学和行政法学分析［J］.上海经济研究，2012（2）:70－76.

［10］张维迎.博弈论与信息经济学［M］.上海:上海人民出版社，2006.

［11］白竹，李雯.出租车公司管理效率评价分析［J］.交通科技与经济，2014，16（1）:39－42.

［12］洪江涛，陈俊芳.企业动态竞争战略选择的微分博弈分析［J］.上海交通大学学报，2007（12）:1975－1978..

［13］Francisco D Galiana，Alexis L Motto，Francois Bouffard.Reconciling social welfare，agent profit，and consumer payment in electricity pools［J］.IEEE Transaction on Power Systems，2003，18（2）:452－459.