辽宁省高速公路弯沉指标衰减趋势分析
于发袂,何 林
(长沙理工大学 交通运输工程学院,湖南 长沙410114)
随着辽宁省高速公路通车时间的增长,高速公路养护已成为辽宁省高速公路管理工作中的重要部分。截止2008年年底,辽宁省约有60%的高速公路运营时间超过了5年,高速公路的养护维修已逐渐进入高峰期。
1 衰减趋势模型的建立
路面结构的使用性能受荷载、环境等多种因素的影响,由于影响因素的复杂性及路面结构本身存在的差异,导致路面使用性能的衰减会出现多种模式。
国内外对路面衰减模型的研究开展较晚,尤其是对预防性养护体系中的裂缝率、功能性破损、摩擦系数等指标的研究尚未开展。目前,综合分析国内外已建的路面衰减模型,大致可分为三类:确定型模型,概率型模型和其他模型。其中确定型模型是指满足给定条件下,模型能给出唯一结果;概率型模型是考虑到路面性能的不确定性,采用概率方法开发的路面模型,常用的概率模型包括马尔科夫概率转移矩阵和贝叶斯概率方法;其他模型是随着人工智能技术的发展,而产生的路面模型,包括专家系统模型和人工神经网络ANN模型等。其中确定型模型是最常用的路面模型,相关的研究也最多,确定型模型的常用表达式有三类:直线,负指数曲线和S型曲线(如美国南卡拉纳州模型等)。
路面在使用过程中,随着时间的推移,在荷载和环境因素的影响作用下,路面状况不断恶化,使用性能呈逐渐下降趋势。由于影响因素的复杂性和结构本身的差异性,路面使用性能的衰变会出现多种模型。综合国内外的研究成果,我们将路面使用性能的衰变过程归纳为4种典型模式,如图1所示,并总结出适合辽宁省具体情况的衰减模型。
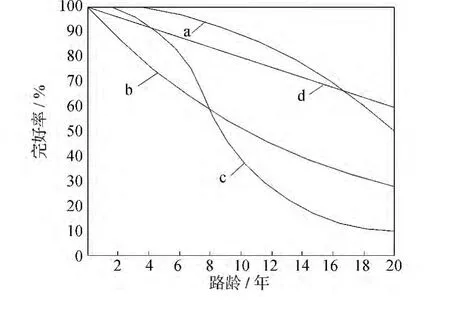
图1 路面使用性能衰减的典型模式
这4种模型曲线的使用性能随使用时间或荷载作用次数的增加呈下降趋势,路况不断恶化,曲线反应的衰变过程有快慢的差异。
1)曲线a为凸曲线,即衰减过程呈先慢后快的模式,国外路面的衰变大多呈这种模式,这在一定程度上反映出路面结构能力及其功能的相关性。路面使用初期,路面结构能力较强,能有效抵抗时间推移和行车荷载、环境因素造成的损坏,损坏速度缓慢。但随着时间的推移和行车荷载作用次数的增加,路面产生疲劳、裂缝、变形等损坏,这些损坏降低了路面的结构承载能力,在荷载和环境的综合作用下,路面使用性能的衰变越来越快。
2)曲线b为凹曲线,使用初期路面性能下降很快,而后期变慢。这种形式在我国的普通公路较为普遍,由于设计和施工的诸多原因,路面投入使用后,很快出现损坏,而损坏的出现会大大降低路面服务能力,养护部门不得不投入较多的资金进行养护,以缓解其恶化速率,使道路在较长的时间内只能以较低的水平提供服务。
3)曲线c为反S型曲线,路面使用初期,由于路面结构抵抗能力较强,路面的损坏较少,服务能力衰变缓慢,而后随着荷载作用年限的增加,损坏速度有所增加,而到了后期路面损坏又趋缓慢,这种形式可以看作是前两种形式的结合,在一定程度上反映出整体强度对路面使用性能的影响。
4)曲线d是直线形式,描述的是路面投入运营后使用性能随使用年限的增加近呈直线递减,路面早期损坏,又缺少必要的养护措施。
影响预防性养护各质量指标的衰减有很多因素,能反映各质量指标衰减规律的方程也有很多种形式,通过对省内高速公路历年检测数据的分析发现,各质量指标与上述4种曲线均存在相应的对应关系,下面我们通过选取典型路段进行举例说明,并研究各质量指标的衰减函数方程。
2 弯沉衰变方程
路面弯沉是路面使用性能的一个重要组成部分,反映了路面结构强度特性,是进行路面养护的重要参数。影响路面弯沉的因素较多,主要有路面结构、水温状况等,这些因素会导致数值的变异性较大,影响对弯沉变化规律进行分析的准确性,所以,只追求数学上的最佳拟合,很难得出合理的结论。因此,只能通过数据衰减趋势的分析确定指标的变化规律,然后选取一些简单且能满足条件的方程,通过对各方程的回归分析,选择较优模型。
为了掌握弯沉的衰减趋势,确定其发展规律,首先将重点观测路段(锦阜高速右幅K56~K76,沈四高速左幅K15~K35,锦朝高速左幅K20~K40,沈阳环城高速右幅K20~K40)2003~2008年路面结构强度指数值绘制成图2。
分析以上4条高速公路重点观测路段路面结构强度的衰减趋势,首先可以确定其衰减形式符合我们总结的4种典型曲线中的曲线a,即衰减趋势为凸曲线,衰减速率呈先慢后快的趋势。通过将检测数据进行回归分析,指数形式的函数曲线和衰减趋势相符程度较好,用指数形式的函数回归以上4条重点观测路段的检测数据,得到的相关性数值分别为:0.959 8,0.992 4,0.972 6,0.988 5。可见,相关性很好,说明指数形式的函数能较好地拟合弯沉实际变化情况,客观地反映出路面使用性能随使用时间的增加而衰减的具体规律。
路面弯沉情况能够反映路面材料的疲劳衰减程度,但是路面材料的疲劳程度难以观测。从宏观来说,路面的损坏程度在很大程度上反映了路面结构的疲劳状态,由于路面损坏状况较容易检测,所以,在建立弯沉衰减方程的时候,方程中应包含反映路面破损状况的因素。路面弯沉的衰减和初始弯沉相关,由于路面结构的不同,不仅初始弯沉不同,其后的衰减速率也会不同,因此,在建立弯沉衰减模型时,也应考虑路面结构的组成。
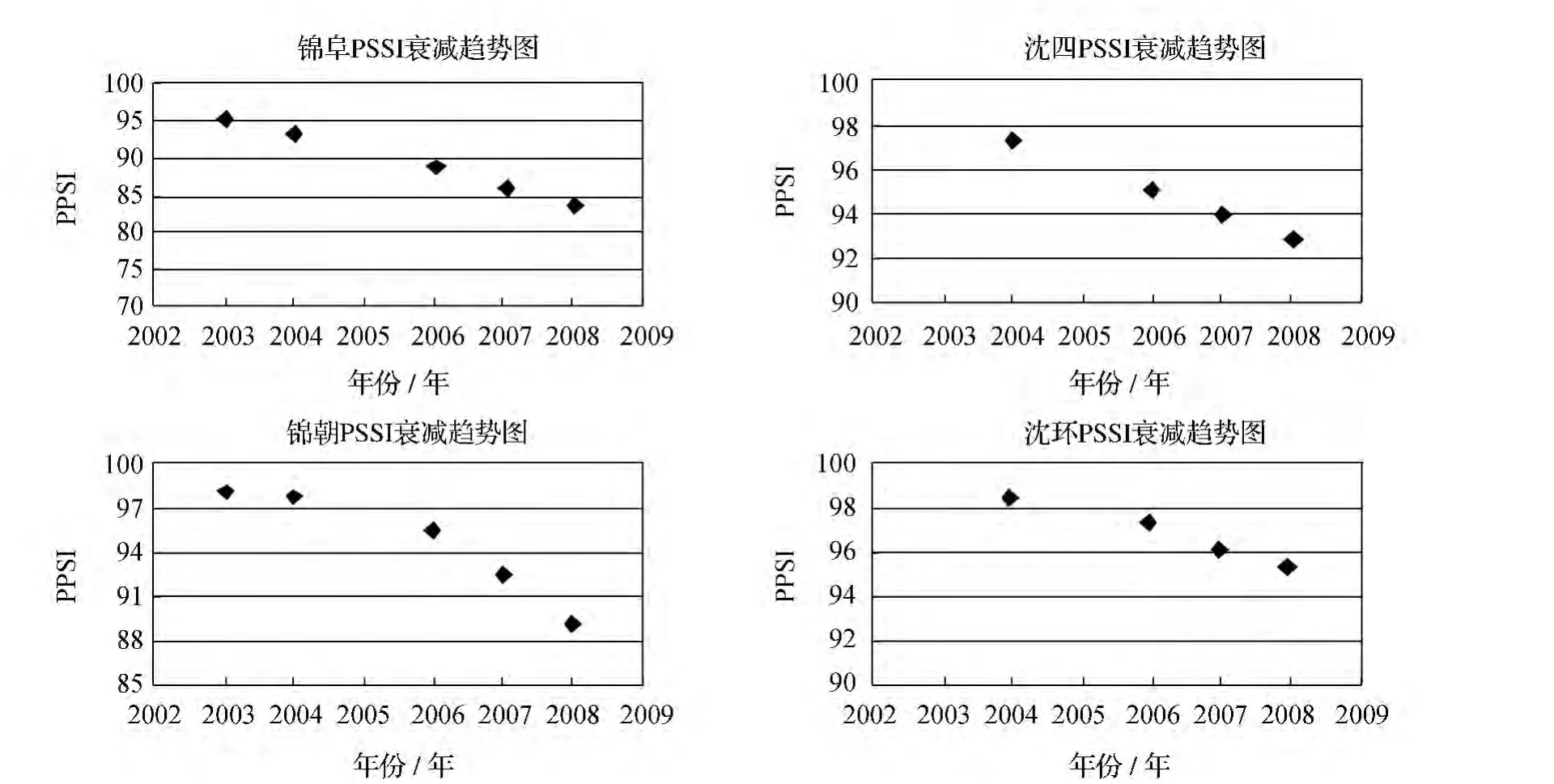
图2 重点观测路段路面弯沉增长趋势
综合以上因素,采用比较方程的形式,通过相关方程的数据回归、曲线比对,确定预防性养护体系中弯沉的衰减模型采用哪一种指数曲线,并最终确定路面弯沉衰变模型的函数形式
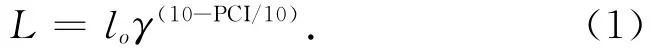
式中:L为路面检测弯沉值;l0为路面初始弯沉值;γ为待定参数,与路面结构有关;PCI为与弯沉相应的路面损坏状况指数。
式(1)中的参数γ为路面PCI每下降10%时路面弯沉增加的百分量,根据实测的PCI和弯沉检测数据可以回归得到γ的数值,再利用所得数值对未来路面弯沉进行预测。当现有检测数据不足或者没有检测数据时,对任意路面结构可以根据以下方法进行计算,首先采用多层弹性理论来计算路面结构的初始弯沉l0,再将路面结构的面层、基层模量折减15%,计算模量折减之后的路面弯沉l′,则有γ=l′/l0,再利用计算后得到的γ值进行未来路面弯沉预测。
式(1)中的PCI为与弯沉相应的路面损坏状况指数,有实际的检测数值时将实测数值代入公式进行弯沉值的计算,缺乏检测数值时使用式(2)对未来的PCI值进行预测,得到PCI预测值后代入弯沉预测模型中,对未来路面的弯沉值进行预测,其相关的计算式为
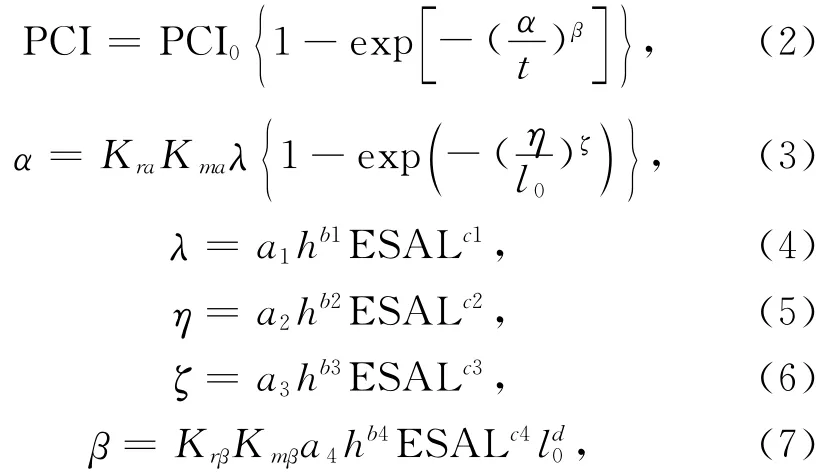
式中:PCI为路面损坏状况指数;PCI0为初始路面损坏状况指数;t为路龄;α为寿命指数;β为形状指数;h为路面沥青层厚度,cm;ESAL为分布日标准轴次;l0为初始弯沉,取0.01mm;a,b,c,d为与路面结构型式相关的经验回归系数;Krα,Krβ为与地区有关的环境影响系数;Kmα,Kmβ为与路面采用沥青类型相关的沥青影响系数。
参数α,β包含了影响路面性能的主要因素,在公式中具有明确的数学、物理意义,参数α的大小反映了路面使用性能的长短,参数β的大小决定了参数的衰减形式。在具有一定数量的检测数据之后,采用非线性回归的方法可以求得两参数值,没有检测数据时可以利用以上公式将两参数值计算得出,并对路面的未来弯沉值进行预测。
3 模型参数标定
3.1 锦阜高速公路
锦阜高速公路右幅K96~K116路段2003~2008年弯沉代表值的平均值如表1所示,PCI评定值如表2所示。

表1 锦阜高速公路观测路段弯沉代表值平均值表
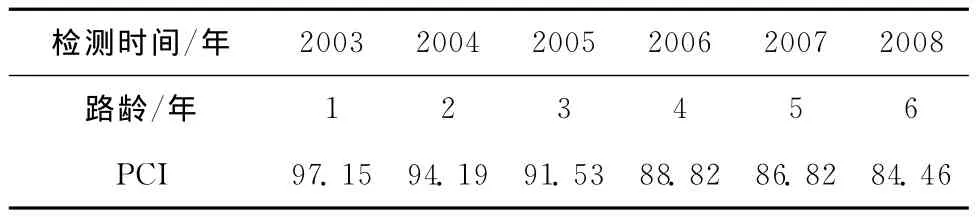
表2 锦阜高速公路观测路段PCI评定值表
通过已有的检测数据对选定函数的参数进行回归,得出选定函数的系数值γ=1.231 7,其相关性R2=0.878 4,得到锦阜高速公路弯沉预测方程的具体形式L=1.231 7l(10-PCI/10)o,运用该方程对锦阜高速公路弯沉发展趋势进行预测,并利用已经检测到的数据对其修正。将锦阜高速公路右幅K96~K116路段2003~2008年的弯沉检测数据和通过以上衰减函数预测的拟定值绘制成图3,通过图3可以清楚地预测弯沉的发展趋势。

图3 K96~K116路段2003~2008年弯沉检测值和拟合值
3.2 沈阳环城高速公路
沈阳环城高速公路2004~2008年右幅K20~K40路段弯沉代表值的平均值如表3所示,PCI评定值如表4所示。
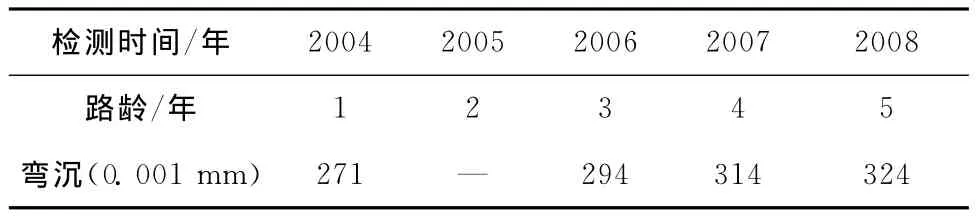
表3 沈阳环城高速公路观测路段弯沉平均值表
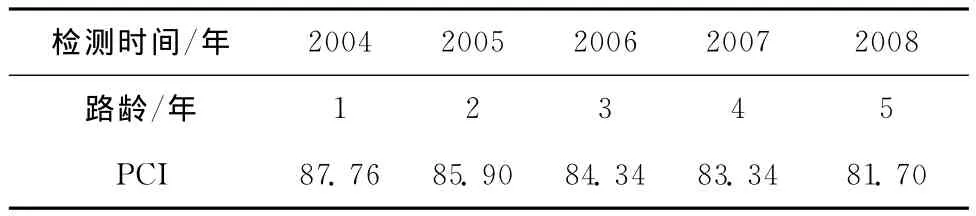
表4 沈阳环城高速公路观测路段PCI评定值表
根据对检测数据的分析结果,衰减函数的回归可得出选定函数的系数值γ=1.627 4,其相关性R2=0.802 9,其中PCI值与弯沉检测年份相应。可得到沈阳环城高速公路弯沉预测方程的具体形式L=1.627 4l(10-PCI/10)o,使用该方程对沈阳环城高速公路进行弯沉发展趋势预测,使用已经检测到的数据对其进行修正。将沈阳环城高速公路右幅K20~K40路段2004~2008年的弯沉检测数据和通过衰减函数预测的拟合值绘制成图4,通过图4可以清楚地了解到弯沉发展趋势。
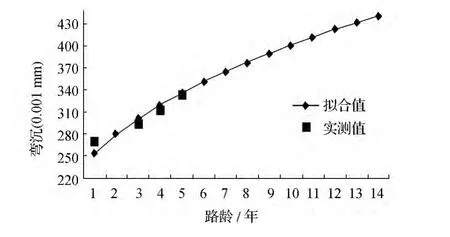
图4 K20~K40路段2004~2008年弯沉检测值和拟合值
4 结 语
通过对比已积累的大量检测数据,参考国内外理论,研究得出适合辽宁省路面实际衰减趋势的模型。通过几条重点观测路段实际检测数据与模型预测值的对比,数据相符程度较好,说明衰减函数适用性较好,形式合理。
通过预测模型绘制的衰减曲线,能清晰地了解路面各指标的情况以及未来发展趋势,体现每条高速公路的路面主要病害情况及发展趋势,能够为公路管理部门制定养护时间,提前做好养护计划。
[1]王阔.高等级公路沥青路面预防性养护评价标准的研究[J].北方交通,2011(4):7-9.
[2]赖万松,于江,李林萍,等.沥青路面微细观结构特性分析[J].交通科技与经济,2013,15(5):97-100.
[3]谭春霞.聚酯纤维改善沥青混凝土路用性能的时效性研究 [D].重庆:重庆交通大学,2009.
[4]李明月.基于全寿命周期的高速公路路面维护方案的优化[D].河北:河北农业大学,2012.
[5]戴洁.高速公路沥青路面预防性养护管理研究[D].长沙:长沙理工大学,2004.
[6]尹吉州.路面结构全寿命周期成本分析方法的研究[D].哈尔滨:哈尔滨工业大学,2005.
[7]张建伟.农村公路养护管理决策方法研究[D].长安:长安大学,2011.
[8]高晓刚.辽宁省农村公路沥青路面养护技术对策研究[D].沈阳:沈阳建筑大学,2010.

