温州市大门大桥主塔施工测量技术

周文健

（中铁大桥局集团第一工程有限公司，河南 郑州450053）

1 概 述

温州市大门大桥是一座跨越乐清湾水道的跨海大桥，工程起于乐清市翁垟镇，连接柳翁公路，向东跨越滩涂及沙头水道，在小门岛西侧南端登陆。线路全线长7.656km，其中大门大桥长6.155km，本桥主跨结构为（135＋316＋135）m双塔双索面PC梁斜拉桥，主塔为花瓶型混凝土桥塔，主塔承台以上高136 m，每塔有22对斜拉索，两塔共176根索。

2 主塔测量控制

主塔的测量控制主要包括三个部分:主桥加密控制网的测设、主塔的测量定位控制、主塔上索导管的测量定位控制。本文主要分析大门大桥主塔的测量定位控制技术、方法及精度。

温州市大门大桥的首级控制网由设计单位布设完成，其平面坐标采用1954年北京坐标系，中央子午线为120°45′00″，高程系统采用1985年高程基准系统。首级控制网的等级为二等，由9个控制点组成。主桥两主塔墩位于大海中间，施工墩位平台时，在其旁边需建设两个试桩平台以及主桥辅墩，利用这些平台及辅墩进行了加密网点的测设，并与首级控制网的三个控制点组成主跨加密控制网，按平面三等级控制网进行GPS测设，并联测跨越南、北主塔水准高程。

2.1 主桥加密网布设形式

主桥加密网形式如图1所示。

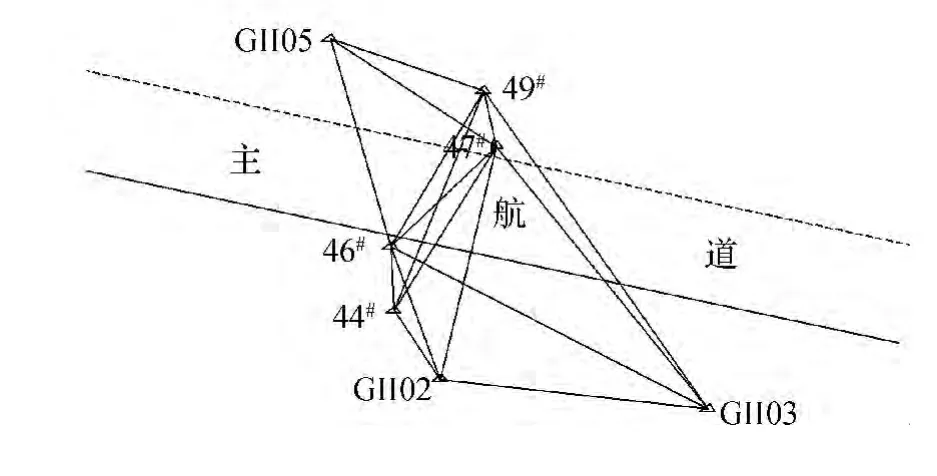
图1 主桥加密控制网

2.2 坐标系统及高程基准

1）平面采用1954年北京坐标系，中央子午线为120°45′00″。另外，在实际测量中，建立相对简明的独立坐标系。

独立坐标系是根据平面转换公式，将大门大桥测量坐标系通过坐标的平移和旋转形成的，以纵桥向轴线为X轴、横桥向为Y轴、标高递增方向为Z轴，使X坐标方向与路线行驶里程保持一致。

2）高程坐标采用1985年国家高程基准系统。

3 主塔的测量定位控制技术和方法

主塔施工测量的重点:保证塔柱、下横梁、中横梁、上横梁、索道管等各部分结构的倾斜度、外形几何尺寸、平面位置及高程满足规范及设计要求。测量难点:在有风振、温差、日照等情况下，要确保塔柱测量精度。定位控制有劲性骨架定位、塔柱模板定位、下横梁定位、中横梁及上横梁定位、索道管安装定位与校核和预埋件安装定位等。

3.1 平面和高程控制测量方法

3.1.1 平面坐标测量

主桥46#和47#墩主塔柱的平面控制测量，依据主桥加密控制网点来进行测量控制和施工放样的。在加密控制点上采用高精度的全站仪、相对基准三维极坐标法进行塔柱的施工放样，包括塔柱模板的测量定位、劲性骨架及钢筋的测量定位、索塔上索导管的安装定位和塔柱节段的竣工检测等。

3.1.2 高程控制测量

依据主桥加密控制网点，在46#及47#墩两主塔承台上精密测设高程基准点，采用TCA1201＋精密全站仪、相对基准差分三角高程精密测量法，进行主塔柱标高的传递和测量控制。

3.2 相对基准极坐标法

在塔柱节段施工过程中的节段模板、劲性骨架等测量定位、塔上索导管的安装定位等测量控制方法，均采用相对基准极坐标法。该方法主要为消除塔柱因日照、温度变化产生的变形而设计的，该法的基准点为索塔塔座及下横梁精密测设的索塔中心点，假设这些中心点已严格位于同一铅垂线上，则可采用相对基准极坐标法放样。该方法包括两步骤:

1）后视基准及距离差分改正方法。采用塔座处经过精密定位的索塔中心点，该点经过精密测量平差计算后得到的坐标，精度很高，消除部分粗差，此点后视更能保证放样点与索塔中心点的一致。

虽然塔座和岸上强制观测墩相对稳定，但索塔实测距离往往与真值存在误差，此误差是平差、气象改正不严密引起的，若将此误差按比例加到观测边长上，则相当于将观测边长改正到平差计算的基准面上，此种处理方法可以提高测量精度。

距离差分改正是在有稳定基准点的条件下，提高测量精度的一种方法，也常用在变形监测中，其计算式为

式中:Δdi为强制观测墩中心至塔座中心点的理论计算距离与实测距离之差，再按式（1）修正实测距离，即可得与平差基准更一致。

2）位于下横梁或相应高程塔柱上精密测设的中心点称为变形基准点，在经过后视基准定向后，每次实测下横梁中心点，再经过距离差分改正和高程面投影改正计算后，得到下横梁或相应高程面塔柱中心点的实测坐标，其与投影时精密测定的坐标之差，可认为是索塔在观测时的实际变形值。

然后，测量待定点与测站点间距离，进行距离差分改正和高程面投影改正，求得待定点初始坐标，再加上求得的索塔变形改正值，即可得出待定点最终考虑索塔形变时的坐标。另外，根据变形监测结果，如果索塔变形改正值很小，可不用此法改正，直接以强制观测墩后视塔座基准定向，采用一般的极坐标法放样即可。

3.3 差分三角高程法

大门大桥主塔处于海中，普通水准仪很难进行高程测量，因此主塔高程控制采用相对基准差分三角高程精密测量法。为了减少在施测中一些误差（大气折光误差等），采用差分技术，在塔座、下横梁和中横梁上布设高程控制点，精密测定控制点高程，以索塔高程控制点作三角高程后视，实时求得待测点相对于后视点的高差。由于观测视线所通过的环境与后视基本相同，大气垂直折光误差可基本消除。

三角高程单向观测高差计算式为

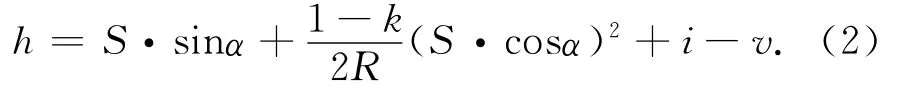
式中:S为斜距，a为垂直角，k为大气折光系数，i为仪器高，v为棱镜高，R为地球曲率半径。

从式（3）、式（4）分析，因前视点与后视点基本在一个竖面上，近似认为k值和平距基本相同，式（3）和式（4）中第二项和第三项为零，且测试前后仪器高相等，所以高差只受测距和测角误差的影响。全站仪TCA1201＋测角和测距精度高，控制点到索塔的距离约346m，利用TCA1201＋仪器的精度测量进行估算，理论上可达到优于±3mm的精度，完全能满足对索塔标高控制的规范要求。

4 塔柱高程控制测量精度分析

标高测量的传统方法是直接用检定过的钢尺配合几何水准点进行传递，但大门大桥主塔柱较高，施工中高空操作平台较小，采用常规水准测量难度非常大且效率很低。因此，通过方案的比较，塔柱标高测量放样采用高精度全站仪，利用EDM三角高程测量法施测，误差积累小，操作方便快捷，可以有效的保证测量精度和定位速度。

EDM三角高程单向观测高差的计算式:

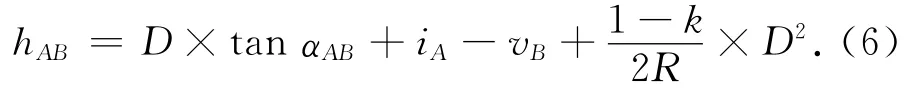
根据误差传播定律:

对EDM单向观测而言，测量过程中影响高差中误差有竖直角测量误差mα、距离测量误差mD、仪器高测量误差mi、目标棱镜测量误差mv和大气折光系数mk。

1）竖直角α和测角中误差mα的影响:

对于全站仪TCA1201＋，竖直角测角精度1″，即mα＝1″。同一测点，水平距离不同导致竖直角α不同，从而由式（8）计算的高差中误差也不同。以索塔高度最大值136m为例，水平不同距离时竖直角对高差中误差的影响数据见表1。

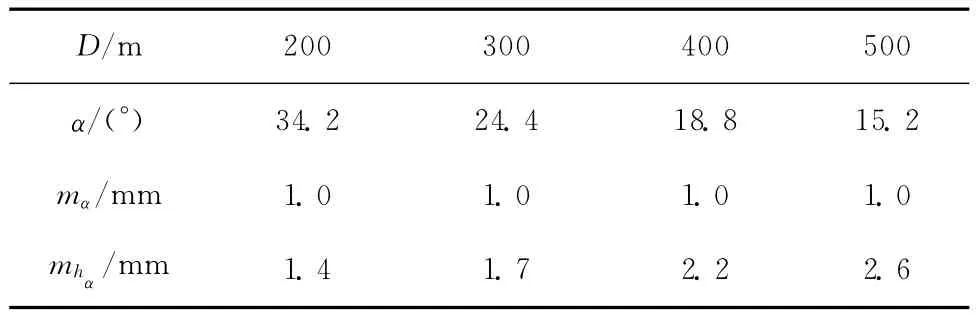
表1 竖直角α和测角中误差mα对mhα的影响

2）竖直角α和测距中误差mD的影响:

TCA1201＋标称测距精度为1mm＋1.5ppm，即mD＝1.8mm，k≈0.14，R＝6 371km，具体取值，见表2。

表2 不同水平距离D对mhD的影响

3）采用强制对中墩方法进行观测，观测过程中，脚架或对中杆高度一般为1mm。

4）mk的影响:

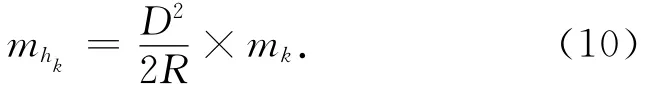
k取值变化幅度很大，一般在0.07～0.32之间（我国常采用经验值0.14），特定情况为负值，数值可取均值一半代入式（8）可算得mh数据如表3所示。

表3 不同水平距离D和值对mh值的影响

5）综合精度分析。根据式（7）分析见表4。

由表4可知，随着水平测距D的增大，mh值随之增大。在全站仪站点位于索塔500m半径以内（即水平测距D≤500m），EDM三角高程的测量精度可以满足《公路桥涵施工技术规范》（JTG TF50／2011）中对误差的精度要求。

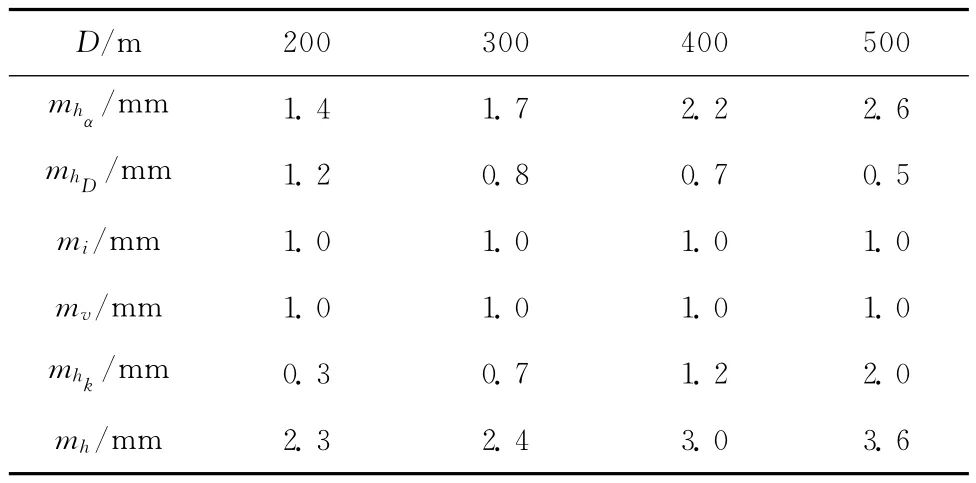
表4 综合精度估算

5 结束语

温州市大门大桥是跨越乐清湾水道的海上最长桥梁之一，该项目的建成将有利于大小门岛发展成临港产业基地，并有利于增强温州港的社会地位。通过实践证明，海上斜拉桥的主塔施工测量，采用相对基准三维极坐标法和相对基准差分三角高程法进行塔柱平面及高程的测量控制，其测量精度和放样误差完全能满足相关规范的要求。该法既保证了工程施工的质量和精度，又方便操作易行，提高工作效率，加快了工程施工进度，起到了良好的经济效益。

［1］徐绍铨.GPS测量原理及应用［M］.武汉:武汉测绘科技大学出版社，1998.

［2］刘绍堂.建筑工程测量［M］.郑州:郑州大学出版社，2006.

［3］肖根旺，许提多，周文健，等.高精度三角高程测量的严密公式［J］.测绘通报，2004（10）:15－17.

［4］刘志强，刘全海，王解先，等.城市CORS参考站稳定性监测与区域地表变形分析［J］.测绘工程，2013，22（4）:80－84.

［5］马洪磊，刘成龙，宋韬，等.自由测站方法在平面控制网测量中的应用［J］.测绘工程，2014，23（5）:51－54.

［6］姚殿梅，周彬.红外线在道路测试中的应用［J］.交通科技与经济，2013，15（3）:45－48.

［7］程飞，张丽娜，张晓亮.全站仪和GPS一体化测量方法探讨与精度分析［J］.测绘工程，2014，23（4）:69－71.