新陈代谢GM(1,1)模型在建筑物沉降监测中的应用
杨晓松,张双成
(1.贵州省黔南州水利水电勘测设计研究院,贵州 都匀558000;2.长安大学 地质工程与测绘学院,陕西 西安710054)
变形监测是把握建筑物的实际性状,科学、正确、及时地分析和预告工程建筑物的变形情况,对工程建筑物的施工、运营和管理极为重要。通过变形监测,把握工程建筑物的稳定性,为安全运行诊断提供必要的信息,及时发现问题并采取措施。
沉降预测是变形监测的主要内容之一,灰色系统理论在建筑物变形分析与预报中被广泛使用,采用新陈代谢GM(1,1)模型,对都匀市某在建大楼的沉降进行了定量分析和预测,这对于工程的施工安全和有效管理具有重要意义。
1 新陈代谢GM(1,1)灰色预测模型
1.1 模型建立
灰色系统预测的基本思路:把随时间变化的一组随机正序列,通过适当的方式累加,成为非负递增的数据序列,利用适当的曲线逼近拟合,以此曲线作为预测模型,对系统进行预测,具体步骤为
1)建立传统的GM(1,1)模型。设等时间间隔序列t1,t2,…,tn,将已测得的变形数据作为原始数据序列:x0={x0(1),x0(2),…,x0(n)},对原始序列进行一次累加生成运算即得到一组新的数据序列,称为累加生成数据序列:x1={x1(1),x1(2),…,x1(n)}。
对单变量序列x1建立一阶微分方程:
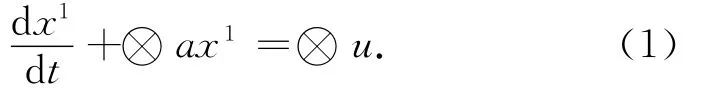
式中:⊗a,⊗u为灰参数,⊗a称为“发展系数”;⊗u为“灰作用量”,其白化值为^a=(a,u)T,用最小二乘法求解得
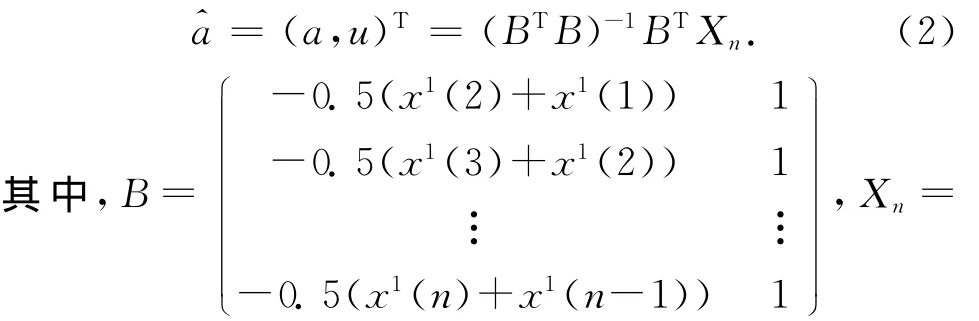
(x0(2),x0(3),…,x0(n))T.
求出后代入式(1),求解微分方程得
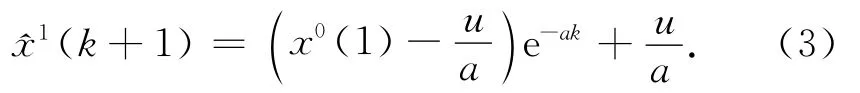
对1(k+1)做累减生成,得到原始数据序列的还原值:
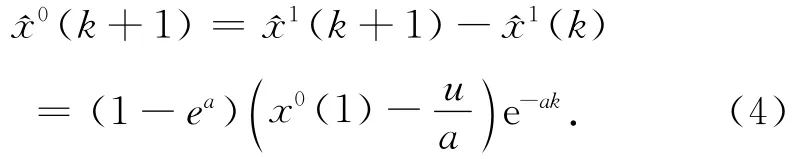
2)改进传统模型。录入最新信息x0(n+1),去掉最老信息x0(1),用新序列
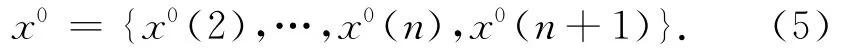
重复步骤一,即得到新陈代谢GM(1,1)模型。
1.2 模型精度检验
新陈代谢GM(1,1)模型通过精度检验,才能进行有效的预测,这里采用后差检验法。
计算预测值0(k)与实测值x0(k)之间的残差:
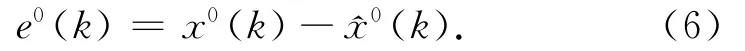
根据式(5)和式(6),计算原始序列向量x0和残差向量e0(k)的方差,得
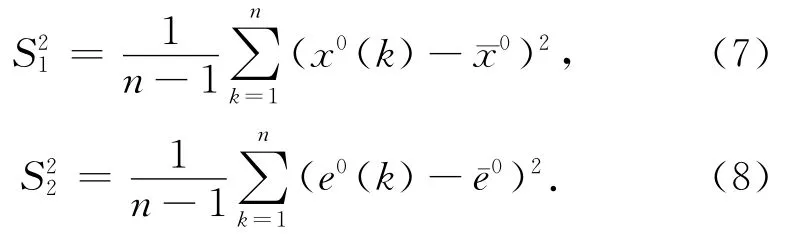
后验差比值:

小误差概率:
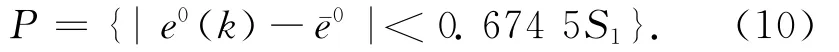
对模型精度的估计,可参见表1。

表1 后验差模型精度等级参照表
2 应用实例
2.1 实例计算及分析
为掌握都匀市某在建大楼的沉降情况,相关单位从2013-06-01—2013-08-31对其进行了监测,间隔时间为一周,监测14期,监测数据见表2。选用监测1号点的原始数据进行灰色预测,前10期监测数据作为原始数据列,后4期数据进行预测验证,具体过程通过使用matlab软件编程实现,其运算结果如表3所示。
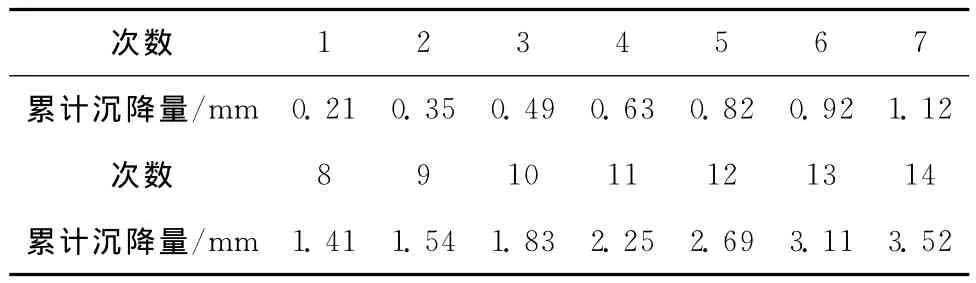
表2 沉降点1的14期沉降观测值
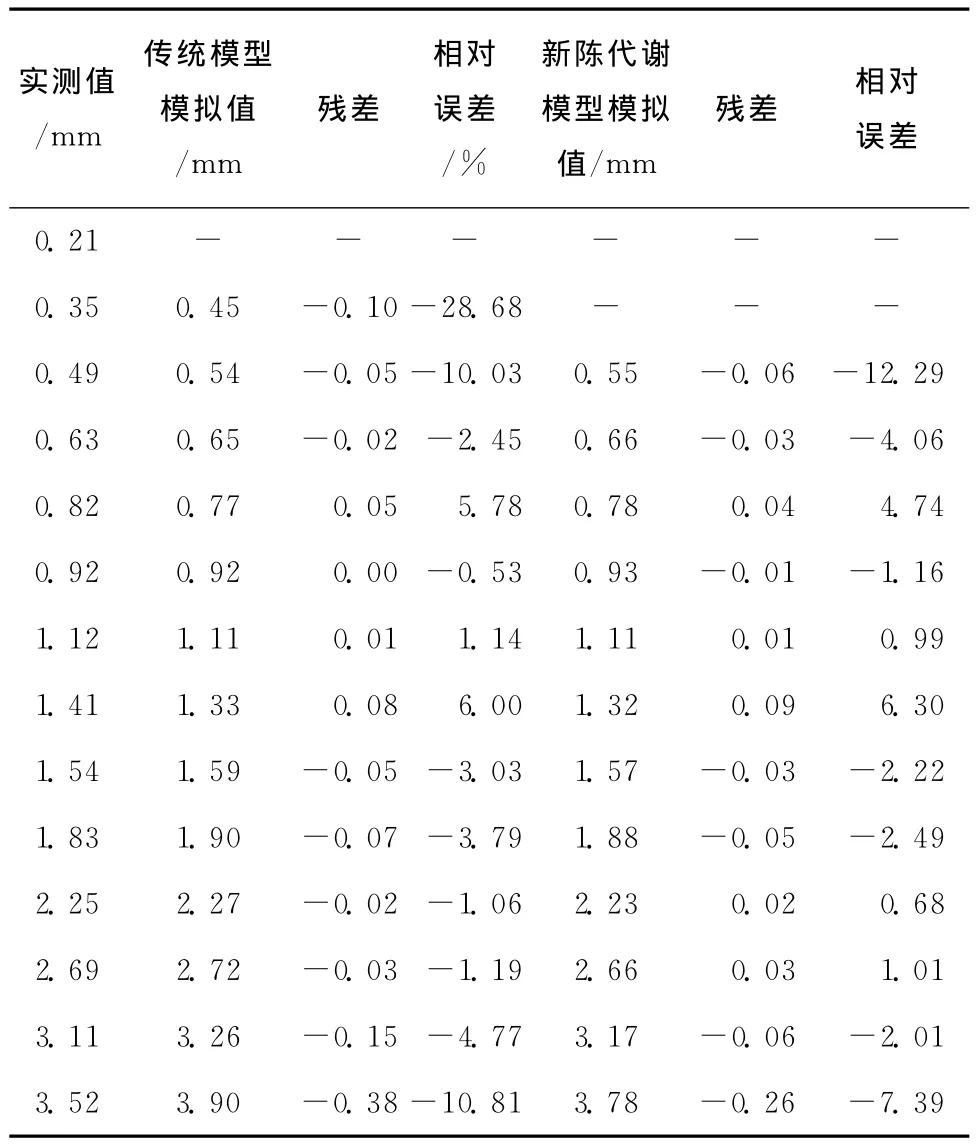
表3 高层建筑物累计变形监测数据及新陈代谢GM(1,1)预测数据表
1)以前10期监测数据作为原始数据建立GM(1,1)模型。
原始序列
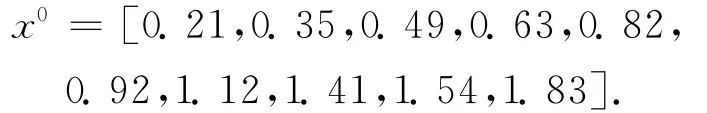
灰参数白化值向量
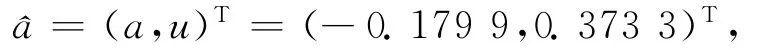
则得到预测模型为
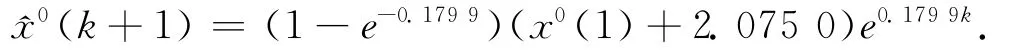
模型精度检验:C=0.105 2,P=1.000 0,由表1可知,C与P均为优。
2)第11期的最新信息,去掉第1期的最老信息,则原始序列变为
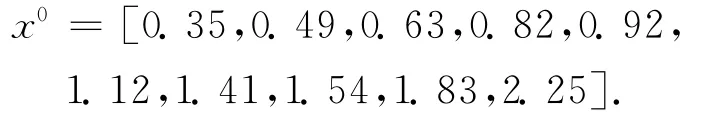
灰参数向量自化值
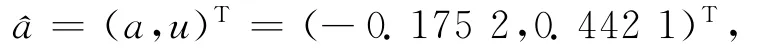
则得到预测模型为0(k+1)= (1-e-0.1752)(x0(1)+2.523 4)e0.1752k.模型精度检验:C=0.080 3,P=1.000 0,由表1可知,C与P均为优。
2.2 预测结果分析
从表3的点1沉降预测结果可以看出,新陈代谢GM(1,1)模型预测精度较高,后3期的预测结果显示:残差绝对值最大为0.26mm,相对误差绝对值最大为7.39%。模型预测的后验差比值C=0.080 3,小误差概率P=1,检验程度为优。与实侧值对比如图1所示,可以看到拟合值曲线光滑,实测值在拟合曲线附近波动,拟合效果良好。
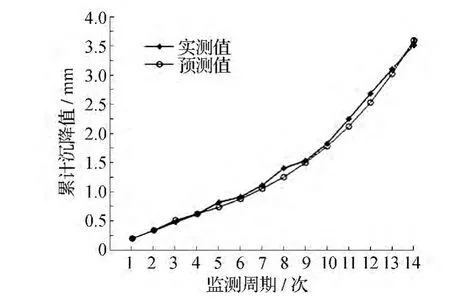
图1 沉降累计变形实测值与预测值
3 结束语
影响建筑物沉降的因素很多,建立模型难度较大,将灰色模型预报技术用于变形监测沉降预报的研究结果表明其拟合及预测精度较高,尤其是动态的灰色预测模型,与传统模型预测相比,其精度更高,更能反映实际情况,预测结果更具有准确性。从工程实例的计算结果与实测结果对比分析来看,它较好地反映了建筑物沉降的基本变化趋势,可提前预测、作出预警,以判定是否超出允许范围,是否安全可靠,这对于建筑物的安全问题具有十分重要的意义。
[1]刘丹丹.灰色模型分析法在高层建筑物变形监测预测中的 应 用 [J]. 测 绘 与 空 间 地 理 信 息,2014,37(2):203-205.
[2]唐争气,谭志强.灰色时序组合模型在基坑检测中的应用[J].测绘工程,2014,23(2):49-53.
[3]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.
[4]黄召杰,冯硕.灰色预测模型在铁路客流预测中的应用[J].交通科技与经济,2014,16(1):57-60.
[5]陶本藻.测量数据统计分析[M].北京:测绘出版社.1992.
[6]李年奇,张俊中.GM(1,1)模型在建筑物变形监测中的应用[J].测绘与空间地理信息,2013,36(8):258-260.
[7]薛山.MATLAB基础教程[M].北京:清华大学出版社,2011.
[8]邱伟,黄腾,朱春宁.混合模型在沉降监测中的组合预测方法[J].测绘工程,2014,23(4):51-54.

