埋地管道极限悬空长度计算

冉龙飞，高文浩，吴 栋，马天骄

（辽宁石油化工大学，辽宁 抚顺113001）

0 前 言

管道运输是油气资源配送的主要方式，在国民经济中占有重要地位。近年来，随着西气东输等一批长距离油气输送管线的建成和投产，国内管线已全网贯通，并与国外的油气资源管线相接。由于管道输送介质易燃易爆等特性，一旦失效，就必然造成灾难性人员伤亡和经济损失，并污染管道周围环境。因此，保证管道安全可靠运行对实际生产生活具有重要意义。

国内管道失效形式很多，管道悬空是管道失效的主要形式之一。造成管道悬空的主要原因有：①由于地面塌陷、地震等灾害造成的地壳内部构造变化导致的管道悬空；②由于滑坡、泥石流等灾害造成的地壳外部环境突变导致的管道悬空；③由于冻土、盐渍土等特殊土体导致的管道悬空。

在长输管线运行过程中，受到外界各种载荷的作用，导致管道处于悬空状态的案例时有发生。如2010年，兰—成—渝输油管道德阳段管道受洪水冲刷，管道大面积悬空，管道多处被拉断，导致部分管线停输，造成严重损失。通过力学计算，其允许的极限悬空长度为44.8 m，但实际悬空380 m管道仍未发生断裂。说明对处于悬空工况下的管道应力分析已不能满足实际的分析要求。

本研究通过理论计算得出悬空管道的极限应变和容许应变，并应用ABAQUS有限元分析软件模拟在管道不同悬空长度下管道的应变取值。当应变取值接近理论计算得到的容许应变值时，对应的管道悬空长度为该管材管道的极限悬空长度，以此作为管道工程评定的标准，保证管道的安全运行[1-2]。

1 埋地悬空管道应力和应变的理论计算

1.1 力学模型的选择

在实际工程模拟计算中，悬空管道力学模型可简化为以下三种类型：

（1）简支梁模型。该模型仅考虑悬空段管道的受力情况，不考虑管－土之间相互作用对未悬空段管道的影响。

（2）弹性地基梁模型。该模型将管道未悬空段看做半无限长符合Winkler假设的弹性地基梁，即认为两端未悬空段的土壤物性、管道及管道变形关于中心对称。

（3）弹塑性地基模型。该模型认为管道处于悬空工况时，受自重载荷、输送介质重力载荷等多种均布载荷的共同作用，使管道产生挠曲变形，而且埋地段管道由于受到管道轴向收拉伸力及土壤阻力作用，是管道产生弯曲变形[3]。

上述三种方法，简支梁模型未考虑悬空段与未悬空段之间的相互影响，全弹性地基梁模型仅考虑了管道的弹性变形，未考虑管道的塑性变形，均与实际情况不符。因此采用弹性地基梁模型，既考虑了悬空管道的弹性变形和塑性变形，又对埋地悬空管道的实际受力情况作了简化。

1.2 应力计算

埋地悬空管道的受力简化模型如图1所示。由图可见，埋地管道悬空段受到均布荷载q作用。均布载荷包括管道自重、输送介质质量和悬空管道埋入端上方土对管道的压力等。管道两端受到当量轴向力S0的作用，当埋地管道悬空长度为L时，管道埋入端受到弯矩M0的作用。在实际分析计算时，将悬空管道两端非悬空段看作半无限长符合Winkler假设的弹性地基梁，近似认为土壤物性、埋地管道的受力和变形关于c-c轴对称[4]。

图1 埋地悬空管道的受力简化模型

悬空管道的挠度微分方程为

式中：E—弹性模量；

I—惯性矩；

M0—管道在x=0处的弯矩；

v0—管道在x=0处的挠度；

q—管道所受载荷；

L—管道悬空长度；

S0—悬空管道的当量轴向力，S0=N0-Np，

N0—管道轴力，拉力为正值，压力为负值；

p—管道承受的内压；

d—管道内径。

根据埋地悬空管道土壤物性、受力的对称性以及边界条件，可得管道在x=L/2处的挠度为

1.3 应变计算

基于应力的管道强度设计方法一般适用于以应力为控制参量的载荷作用下的弹性设计。而基于应变的设计方法一般适用于在发生地震、塌陷、洪水、滑坡等重大地质灾害时，管道会发生变形，此时作用在管道上的载荷是以位移为控制参量来衡量的。采用基于应力的设计方法难以使管道满足强度设计的要求，因此，将基于应变设计方法的作为基于应力设计的补充。两种设计方法的工作区域和控制参量不同，导致计算过程也不相同。

基于应变的设计方法主要是确定管道处于悬空状态时将要承受的容许应变和管道本身的极限应变。为防止在悬空状态下管道过量变形使管道出现裂纹，甚至拉断，导致管道失效，在实际理论计算过程中，存在拉伸应变、压缩应变和椭圆化变形三种类型的应变[5]。

1.3.1 拉伸应变

管道处于悬空工况时，可能存在缺陷，拉伸应变取值达到或超过极限应变取值时，可能导致管道断裂，拉伸应变取值应满足（3）式要求

式中：εtf—纵向或周向的因子化拉伸应变；

φεt—拉伸应变阻力因子；

εtcrit—管壁或焊接部位的极限拉伸应变。

拉伸极限应变依据CSA Z662—2007[6]计算得到，容许拉伸应变的阻力因子取值为0.7。

1.3.2 压缩应变

管道悬空时未悬空段管道承受压缩载荷或者弯矩，管道会产生压应力和应变，当管壁最大压应变达到或者超过临界水平，管壁会出现局部屈曲或褶皱。因此，压缩应变取值应满足（4）式要求

式中：εcf—纵向或周向的因子化压缩应变；

φεc—压缩应变阻力因子；

εccrit—轴向或周向压缩极限应变。

依据CSA Z662—2007，容许压缩应变的阻力因子取值为0.8。

当考虑内压时，压缩应变应按照（5）式计算

式中：t—管道壁厚；

D—管道外径；

pi—最大设计内压；

1.3.3 椭圆化变形

依据美国船级社（ABS）设计规范，为防止管道严重椭圆化导致局部屈曲，应变极限满足（7）式要求

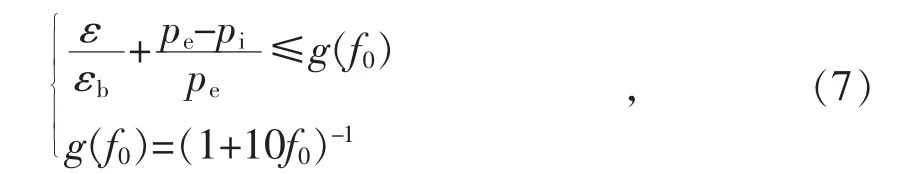
pe—最小外部静水压力；

Es—管道的弹性模量；

Fy—最小屈服强度。

当不考虑内压时，依据薄壳褶皱理论，许可压缩应变为

式中：ε—弯曲应变；

εb—管道纯弯曲时的屈曲应变；

f0—外圆率，运输过程中要

求f0不超过0.75%。

2 有限元分析

埋地管道随土层运动而发生变形，基于埋地悬空管道的受力特点，应用ABAQUS有限元分析软件进行模拟计算。ABAQUS是一套功能齐全的工程模拟有限元分析软件，可以解决模拟件结构的各种问题，范围包括从简单的线性分析问题到复杂的非线性分析问题。ABAQUS针对埋地管道开发了专门模拟管道与周围土壤之间相互作用的虚拟单元，即管－土相互作用单元（PSI）。ABAQUS提供的管－土相互作用单元包括：二维单元PSI24和PSI26，三维单元PSI34和PSI36。埋地管道的模拟可以用梁、管或弯接头单元来进行，地基受力和管道与周围土壤之间的相互作用通过PSI单元来模拟。管－土相互作用单元如图2所示，PSI单元与下面模拟管道的梁、管或弯接头单元共用节点，地面的实际运动情况在模拟过程中通过施加边界条件来加以描述[7-8]。

图2 管－土相互作用单元简图

在不考虑风载荷、温差、外界震动、初始装配应力等其他因素影响，对悬空管道受力情况进行模拟分析，确定采取何种单元来模拟悬空管道的实际受力情况。ABAQUS可供选择的模拟单元有梁、管或弯接头单元。本研究采用梁、管单元的实际受力情况。ABAQUS可供选择的模拟单元有梁、管或弯接头单元。本研究采用梁、管单元来模拟埋地悬空管道的受力情况，根据悬空管道的受力特点采用弹塑性地基模型，对悬空管道的实际工况进行简化来模拟。在计算过程中管－土之间的相互作用通过在管单元节点上的轴向土弹簧、竖向土弹簧和水平横向土弹簧来近似代替。土弹簧模型如图3所示，该模型将管体周围土层简化为等效弹塑性弹簧，通过弹簧刚度和自由度来定义管－土之间的作用。土弹簧刚度依据 《油气输送管道线路工程抗震技术规范》（GB 50470—2008）附录E要求计算得到[9]。管－土相互作用属于非线性问题，应用ABAQUS有限元分析软件能模拟非线性计算非线性问题。

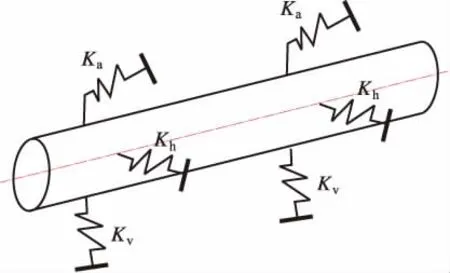
图3 土弹簧模型简图

3 算 例

悬空埋地管道管材为X70，管道外径1219mm，壁厚为18.4 mm，管材密度为7 800 kg/m3，弹性模量为206 GPa，泊松比为0.3，设计系数为0.72，管道的最小屈服强度为485 MPa，管道的工作压力为10 MPa。管道安装时的温度为27℃，发生悬空时的温度为23℃，管道埋深为1.5 m，土体密度为1 700 kg/m3，土的内摩擦角为30°，地基系数k0=4×104kN/m。计算得到管道自重为55.1 kN/m，管道上方土壤的重力为48.9 kN/m，单位长度横向土弹簧刚度为7.15×105N/m2，垂直向上土弹簧刚度为2.68×105N/m2。在不考虑轴向载荷的情况下，应用ABAQUS软件计算得到在不同悬空长度下管道的应力、应变和挠度取值见表1[10]。

表1 不同悬空长度下管道ABAQUS有限元分析的数值计算结果

图4 不同悬空长度下管道的应力变化曲线

应用ABAQUS有限元分析软件得到该工况下管道的数值解，可见随着管道悬空长度的增加，最大应力，最大位移以及应变值都增大。该管材管道在不同悬空长度下管道的应力变化曲线如图4所示。

通过理论计算得到管道的极限压缩应变取值为0.77%，容许压缩应变取值为0.62%。软件模拟得到管道的应变取值接近管道的容许压缩应变时对应的悬空长度取值为350 m。管道悬空长度超过该值时，管道可能被拉断，存在安全隐患，应采取防护和监测措施。

4 结 语

对于处于悬空工况下的埋地管道，应力分析不能满足实际要求，采用基于应变的分析方法能对处于变形的管道作出安全评定。对于算例中的管材而言，当管道的极限悬空长度达到350 m时，管道的应变值为0.61%，接近管道的最大允许应变，一旦超过该应变值，该管材的管道可能被拉断，存在安全隐患。因此在实际工程中，可将极限悬空长度作为管线运行的安全评定准则。

［1］由小川，庄茁.高压天然气管线在地质灾害下的失效分析［J］.天然气工业，1999，19（04）：77-81.

［2］王沪毅.输气管线在地质灾害中的力学行为研究［D］.西安：西北工业大学，2003.

［3］马廷霞，吴锦强，唐愚，等.成品油管道的极限悬空长度研究［J］.西南石油大学学报（自然科学版），2012 （04）：165-173.

［4］罗金恒，赵新伟，王峰会，等.地质灾害下悬空管道的应力分析及计算［J］.压力容器，2006，23（04）：23-26.

［5］王峰会，赵新伟.高压钢管黄土塌陷情况下的力学分析与计算［J］.油气储运，2004，23 （04）：6-8.

［6］ CSA Z662—2007，Oil and Gas Pipeline System［S］.

［7］符圣聪.用于埋管抗震计算的地面位移和地基反力系数［R］.北京：中国建筑科学研究院，1996.

［8］邢静忠，柳春图.线弹性土壤中埋设悬跨管道的屈曲分析［J］.工程力学，2008，25（10）：72-75.

［9］王小龙，姚安林.埋地钢管局部悬空的挠度和内力分析［J］.工程力学，2008，25（08）：218-222.

［10］唐永进.压力管道应力分析［M］.北京：中国石化出版社，2003：96-97.