基于多重回归模型的住院人数预测

三峡大学人民医院信息科（443000） 覃 桓

基于多重回归模型的住院人数预测

三峡大学人民医院信息科（443000） 覃 桓

目的寻长合适的预测方法预测住院人数。方法以上一年度的住院人数及本年平均开放床位增加数为自变量建立多重回归模型预测本年住院人数。结果建立的多重回归模型具有极高的拟合程度。结论用此种模型预测住院人数在置信度一定的前提下置信区间窄，具有科学性和实用性。

多重回归 住院人数 预测

准确合理的预测医院住院人数对医院管理者指导工作、制定工作计划、做出科学决策提供有效依据；在实际工作中一方面有利于医院管理者合理利用人力、财力、物力，减少工作中的盲目性，另一方面能更有效合理的分配各项资源，为病人提供更优质、高效的服务。

资料与方法

1.资料来源

资料来源为本院2000-2011年的统计资料，资料包含住院人数、平均开放床位增加数（表1）。平均开放床位增加数为本年平均开放床位数减上年平均开放床位数。资料通过本院HIS系统收集汇总，有统计台帐、统计报表存档，另有原始数据备份，数据真实可靠。

表1 三峡大学人民医院2000-2011年住院人数和平均开放床位增加数表

2.预测方法

预测方法为以上一年度的住院人数及本年度的平均开放床位增加数为自变量，以本年度的住院人数为应变量建立多重线性回归方程。上一年度住院人数在完成上一年度住院人数统计工作后取得，本年度平均开放床位增加数在医院没有增减病床计划的情况下为零，如本年度有增减病床数计划，则根据病床增减的时间及床位数可以准确测算。以上两个自变量均可在年初取得，预测方法切实可行。

（1）预测模型

建立多重线性回归方程对原始资料拟合。

（2）预测方程

利用OLS估计式求得，建立回归方程。

（3）统计结果分析

方差分析结果F＝111.327，P＜0.01，说明该回归方程具有统计学意义。

计算t统计量得到关于b1的t统计量t1＝13.063，P1＜0.05，b2的t统计量t2＝2.480，P2＜0.05，说明方程引入的两个自变量均有统计学意义。

复相关系数R＝0.983，决定系数R2＝0.965，计算结果表明此回归方程中应变量与各自变量之间的相关程度极高，各自变量对应变量的解释程度高达96.5%。

预测误差分析

通过分析预测模型的误差来检验预测模型的可靠度是一个必要环节，通过分析误差，观测预测结果是否需要作合适的修正，进而将误差控制在合理的范围之内以提高预测结果的准确性［1-3］。首先分别将各自变量的实际数值代入建立的多重回归模型，计算出预测的住院人数即预测值，然后计算预测值与实际值之差的绝对值即绝对误差及绝对误差占实际值的百分比即百分比误差（表2）。

从表2中可以看出预测值与实际值的百分比误差最大为12.26，最小为0.11，误差较小，预测的效果较好。以5年为一组，2007-2011年的百分比误差合计为18.21，2002-2006年的百分比误差合计为20.38；以3年为一组，2009-2011年的百分比误差合计为5.56，2006-2008年的百分比误差合计为13.57，2003-2005年的百分比误差合计为16.46；从以上数据可以看出相对靠后的年份预测误差小，相对靠前的年份预测误差大，其中相对靠后的年份预测误差小的现象正是实际运用中想要达到的目标，能提高预测结果的准确性。

表2 预测误差分析表

外推预测

2012年平均开放床位增加数为131张。

1.点估计

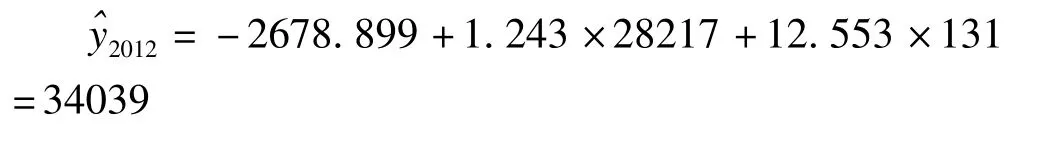
2.区间估计

给定α＝0.05，查表得自由度为n-k＝8的临界值为：

通过以上外推计算得出2012年住院人数的点估计值为34039人，在95%的置信度下预计2012年住院人数的变动范围在30292人至37786人之间。

小 结

1.预测模型考虑到对住院人数影响最大的两个因素，第一个自变量是上一年度的住院人数，利用了自回归的特点，第二个自变量是可以准确测算的当年平均开放床位增加数，合理选取对应变量影响最大的自变量是实现预测精度高、取得预测成功的关键。本院2012年实际住院人数为33218人，与预测的点估计值34039人仅相差821人，预测值与实际值的百分比误差仅为2.47，当然这也与2012年无重大疫情，未出现反常天气现象等有密切关系。

2.近3年的住院人数同比增长幅度明显高于以前年度的同比增长幅度，主要是因为近年来我国国民经济高速增长及国家相关医疗体制改革政策的出台，这也是回归方程b0为负的原因，因此在对住院人数进行统计预测的时候还必须考虑国家相关医疗体制改革政策的变动及国民经济高速增长的前提条件是否发生了明显的转变，如上述因素发生明显的变化，应对预测的结果做适当修正。

3.本预测模型不适宜做过长时间的预测，原始数据的跨度也不宜过长如数十年的历史资料，因住院人数受影响的因素极多，有些在数年内不能明显体现的特征，在数十年的变化中则产生较为显著的影响，相对短期的资料能减少其它长期因素的影响，使得预测的效果更理想［4-5］。

4.虽然统计预测是建立在严格的数学理论之上，但是现实世界中有很多现象与数学理论并非完全相符合，因此在做统计预测的时候不仅要利用已知的数据和方法进行点值估计，还要给出预测期实际值的可能范围（上、下限值）和预测期实际值在这一范围内的把握程度（置信水平），即区间预测［6］。本文利用多重回归模型预测了2012年住院人数点估计值和一定把握性下的区间估计值，预测结果体现了把握性和准确性的统一。

5.在实际的工作中对同一个指标可能存在多种预测方法且均存在合理的解释，在预测时应选择解释程度高的预测方法进行预测。笔者结合医院住院人数变动的特征建立的多重回归模型，达到了很好的预测效果。国内外有学者报道采用以前年度的住院人数、门诊量、手术量等数据来预测住院人数，但相关系数不及本模型，同时预测的准确率也会相应较低，估计的区间也会相对较宽，本预测方法的精度较高，具有一定的实用价值。

1.Rogerson PA.Weight estimation and significance testing for three focused statistics.Statistical methods in medical research，2012，21（5）：433-444.

2.Gerds TA，Scheike TH，Andersen PK.Absolute risk regression for competing risks：interpretation，link functions，and prediction.Statistics in medicine，2012，31（29）：3921-3930.

3.Whitaker HJ，Hocine MN，Farrington CP.The methodology of self-controlled case series studies.Statisticalmethods in medical research，2009，18（1）：7-26.

4.Sun Y，Teow KL，Heng BH，etal.Real-time prediction ofwaiting time in the emergency department，using quantile regression.Annals of emergency medicine，2012，60（3）：299-308.

5.Crabtree BF，Ray SC，Schmidt PM，et al.The individual over time：time series applications in health care research.Journal of clinical epidem iology，1990，43（3）：241-260.

6.Julious SA，Owen RJ.A comparison of methods for sample size estimation for non-inferiority studies w ith binary outcomes.Statisticalmethods in medical research，2011，20（6）：595-612.

（责任编辑：郭海强）