二分类数据缺失多重填补分析及应用*

山西医科大学公共卫生学院卫生统计教研室（030001） 张 耀 陈培翠 张翠仙 罗天娥 刘桂芬

二分类数据缺失多重填补分析及应用*

山西医科大学公共卫生学院卫生统计教研室（030001） 张 耀 陈培翠 张翠仙 罗天娥 刘桂芬△

目的阐明四种填补方法（multiple imputation，M I）的基本原理，实例介绍纵向研究二分类缺失数据多种填补方法的应用。方法对比分析简单填补、分层填补、考虑个体差异的填补及考虑个体、抽样的多重填补等四种填补方法；模拟证实几种OR取值的敏感性分析。结果进行大样本（N＝10000）模拟研究表明：简单多重填补分析会降低检验效能，不能客观反应两样本的差异；考虑先前信息的分层多重填补会扩大I型错误；若只考虑个体变异，仅模拟一个数据集，所得结论不稳定；在考虑个体、抽样和填补差异后模拟的多重填补数据集，当OR≈2时，所得统计量基本接近真值；实例验证，经高血压知晓干预后，尚不能认为两区的吸烟率有差别。结论不考虑前次观察数据以及OR值的影响，一味地把缺失值当作该事件发生处理，会加大I型错误；只有综合考虑个体、抽样和填补差异，多重填补数据集的估计结果才更具稳健性。

多重填补 纵向研究 二分类数据缺失 效果评价

数据缺失是纵向研究中普遍存在的问题，盲目地对缺失数据进行处理，会丧失原资料蕴藏的信息，甚至得出错误的结论。公共卫生研究中，有关药物依赖、酗酒、吸烟等针对个体纵向监测的干预效果的评价，二分类数据缺失是多见的一种形式。有关二分类缺失数据处理的统计方法，已有非技术性文献发表［1］，但由于这些方法未能在标准分析软件中方便实施，其研究尚有较大空间。本文拟针对二分类数据缺失多重填补问题介绍四种方法。

原理与方法

对于本文，形如nabcd，下角标中第一个值a表示前一观测时间点t0的观测结果是否存在某种行为，赋值：是＝1，否＝2；下角标b表示最后观测时点是否缺失，赋值：是＝1，否＝2；下角标c表示最后一次观测结果是否存在某种行为，赋值：是＝1，否＝2；d表示分组情况；下角标“.”表示两水平行或列的合计；t0表示首次观测某种行为时刻，t1表示干预后终点观测时刻。

1.二分类数据缺失多重填补原理

（1）简单多重填补法（simple M I）

对单一时间点，不考虑前一时刻t0观测结果，根据最终观测结果二分类效应变量如吸烟与否，是否有数据缺失，可列成四格表，其优势比OR＝（n11/n12）/（n21/n22），式中n22表示非吸烟组观察单位数；n21表示吸烟组非缺失个体数，缺失值n12和n11是未知的，其推算式记作：

若将缺失均看作是吸烟，n12＝0，n11＝n1（“.”表示行或列合计所有缺失个体），则OR值趋于＋∞。显然，关于OR值更合理的假设是有限的。当n21/n22值已知，若设定OR值，由式（1）可估算出缺失数据中吸烟与非吸烟的观察单位数。同理将式（1）转换为：

式（2）中，odds1：实际观察到吸烟个体的优势（n21/n22）；π：优势比为OR值时，数据缺失者中吸烟者所占比例，即n11＝n1.π。

（2）考虑先前信息的分层多重填补

考虑先前信息的多重填补（consider previous information MI）中，LOCF（last observation carried forward）是目前众多研究中常用的填补技术，因其原理不合逻辑被广泛批评［2］，它是将最后一次得到的干预效应作为其观察终点。按终点观测前一时刻t0观察结果分层，设某层数据缺失值中吸烟者所占比例为πi，即

式中，oddi：第i层（i＝1，2，…，k）终点非缺失个体吸烟者的优势。

（3）考虑个体差异的多重填补

尽管分层多重填补考虑了前一时间点观测结果对本次结果的影响，但仍没有考虑由于个体变异对观察结果的影响。若在分层条件下再考虑个体变异的多重填补（consider individual variation M I）可用潜变量logistic回归模型［3］表示：

式中，εi：个体差异；Miss：数据缺失＝1，反之赋值为0；Smok0i：当前次观察结果为吸烟者，赋值为1，反之为0；β0表示t0时刻不吸烟，t1时刻非缺失其吸烟的优势对数值；β2：表示t0时刻吸烟，t1时刻非缺失其吸烟的优势对数值；β1表示t0时刻不吸烟，t1时刻缺失其吸烟的优势比对数值，β3：表示t0时刻吸烟，t1时刻缺失其吸烟的优势比对数值（可通过设定的OR值来表示）设为个体i的潜变量，记临界值为γ，如果Y*＞γ，Y＝1，否则Y＝0。通过设置logistic回归模型临界值γ＝0，假定误差εi服从标准logistic分布（均数＝0，方差为π2/3）［4］，对原缺失数据按式（4）进行合理填补，即可将个体变异考虑入填补过程，使具有相同协变量的受试者赋有不同的吸烟概率，该填补也称为随机回归填补［5］。

（4）考虑样本变异的多重填补

基于填补过程中考虑样本的变异（consider sampling variation M I），可用常规logistic回归来预测二分类结果。t0时刻非吸烟个体分层回归参数的方差协方差估计如下：

同理，t0时刻吸烟个体分层回归参数的方差协方差估计类似；我们用表示t0时刻非吸烟者估计的参数向量的估计方差-协方差；假定从均数为和方差-协方差为的总体中进行随机抽样得到的参数。按上述过程，同样可获得t0组吸烟者的回归系数同理，从均数为（即t0组吸烟者回归系数向量为和方差-协方差矩阵总体中进行随机抽样得到的参数（即用n1ij代替n2ij估计得到参数）模型表述如下：

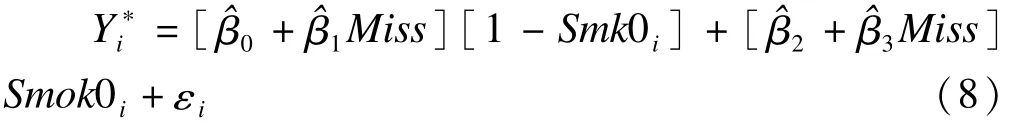
将连续潜变量Y*转化为二分类变量yi，与前规则相同，进行多次重复随机填补，建立多个模拟数据集，即可对感兴趣的效应变量进行统计分析与评价。

有关上述四种方法的模拟证实，无论采用不同的OR值，还是随机获得填补100次的模拟数据集，均可采用SAS9.2编程来实现。

2.大样本模拟研究

进行大样本（N＝10000）模拟研究表明：简单多重填补分析会降低检验效能，不能客观反应两样本的差异；考虑先前信息的分层多重填补会扩大I型错误；考虑个体差异的多重填补所得结果极不稳定；考虑个体变异样本变化的多重填补分析结果最接近真实值，且OR≈2时，所得统计量基本接近真值。

实例研究

1.六社区吸烟干预数据缺失情况分析

以全国社区高血压规范化管理项目太原分中心研究数据为例，收集2007-2008年间太原市迎泽区（师范中心社区、庙前社区和棉花巷社区）与杏花岭区（东华苑社区、敦化坊社区和杏花岭社区）管理的518例高血压患者为研究对象；根据项目组对高危患者实行社区高血压三级管理要求，一年内应进行六次随访；以基线调查中非药物治疗是否吸烟为t0时刻观测结果，以第五次随访吸烟状况为干预后终观测结果。经两地区基线资料吸烟率比较，χ2＝0.914，P＝0.339，尚不能认为两区患者的吸烟率有差别。按项目规范管理要求，经对患者每月集中实施高血压知识、态度和行为等规范管理干预后，进行干预效果评价。

通过对两区六个社区第五次终随访结果吸烟情况分析可知，迎泽区实施三级规范化管理的高血压患者261例，第五次检测中数据缺失95例，缺失比例36.40%；杏花岭区管理257例，第五次检测中数据缺失132例，缺失比例51.36%，两组缺失数据平均占高血压规范管理患者的43.8%。

2.二分类数据缺失四种多重填补方法对比研究

（1）简单多重填补法分析

表1 两区终随访数据缺失关系分析

由基线资料分析，迎泽区吸烟率75/166＝45.1%，杏花岭区吸烟率71/125＝58.8%，经Pearson卡方检验χ2＝3.851，P＝0.0498，可认为两地区吸烟率有差别。若采用简单多重填补，将缺失个体均假设为吸烟，迎泽区和杏花岭区的吸烟率分别为（75＋95）/261＝65.13%和（71＋132）/257＝78.99%，经两区终随访吸烟率比较χ2＝12.331，P＜0.01，尽管统计分析结论一致，但卡方值有很大的差别。可见把缺失值均看做吸烟（或不吸烟）的假设，给两区高血压知晓干预效果的评价解释带来较大的困惑。因两区数据缺失比重不同，这样将数据缺失值都看作吸烟，显然不合理。若考虑数据缺失与吸烟率的关系，分别将OR取值设为1、3、5、7（即缺失数据的吸烟优势是已观测个体的1倍、3倍……），若OR＝1，则π＝1×［（71＋75）/（54＋91）］/（1＋1×［（71＋75）/（54＋91）］）＝0.502，即当缺失与吸烟关系独立；表明缺失数据中吸烟率50.2%，则迎泽区缺失数据中吸烟数为n11＝95×0.502＝47.69；同理，不同OR取值条件下，可填补杏花岭区缺失数据中吸烟与非吸烟观察单位数，见表2。

表2 4种边际OR取值对两组吸烟率的影响分析

表2简单填补法分析结果可见，边际OR取值不同，对分析结果有影响，随边际OR值的增大，更趋于得出两组吸烟率差别有统计学意义的结论。

（2）分层多重填补分析

若考虑第一时点（基线）与终观测结果间的关联性，即基于t0时刻吸烟（Smok0）信息进行分层分析，结果整理如表3。

表3 按Smok0分层多重填补分析

表中，基线调查不吸烟者中，终随访结果迎泽区缺失n21.y＝n212y＋n211y＝62，杏花岭区缺失n21.x＝n212x＋n211x＝64；同理，基线调查为吸烟者中，迎泽区缺失n11.y＝n111y＋n112y＝33，杏花岭区缺失n11.x＝n111x＋n112x＝68。仍假定OR＝1，π1＝（141/137）/［1＋（141/137）］＝0.2303；π2＝0.9292。进行不同OR取值假定下的分层填补，结果对比见表4。

表4 两区不同OR取值分层多重填补结果分析

表4OR取值分别为1，3，5，7的分层多重填补结果表明，OR＝1时，表明数据缺失与效应变量间关系相互独立，而OR＝7表明两者间关联性较强。结果可见，简单填补法更易把分析结果推断为有统计学意义，而分层填补在数据缺失与效应变量有关联时，它可更客观地反映出分层OR值远比边际OR值的影响小，也即干预后效应变量是否有统计学意义，其结果也取决它与缺失数据间的关联性，即将缺失值均看做吸烟的假设掩盖了OR取值的影响。

（3）考虑个体变异的多重填补分析

假定误差分布服从均数＝0，方差为π2/3的logistic分布［4］，按式（4）来拟合logistic回归模型，对所产生的数据集进行分析，模拟分析结果见表5。

表5 考虑个体变异四种OR取值两组结果比较

考虑个体变异，OR分别取值1、3、5、7时分析结果对比表明，由于存在个体变异，不能单纯考虑OR取值对数据缺失与效应变量间关系的影响，尚应计算考虑个体变异情况下含有数据缺失信息吸烟的概率，它是目前填补方法中既考虑逻辑关系，又考虑分析效果解释的首选方法。

（4）考虑个体变异样本变化的多重填补分析

在考虑个体变异的情况下，重复随机填补过程100次生成多重填补数据集，并进行两区干预后吸烟率的比较。

表6 考虑个体变异和四种OR取值样本变化情况的两组比较

填补进行100次，OR取值为1、3、5、7时，计算检验统计量与对应的P值。需要注意的是，相同OR取值时，其卡方值均小于没有考虑个体、抽样和填补差异的卡方值，P值均大于表4、表5的概率P值。由此可知，同时考虑抽样、随机填补和个体变异，且OR取值低于5时，两区高血压规范管理对吸烟知行干预效果尚不能认为有差别；而OR取值不同对应的敏感性分析结果有差别。

小 结

二分类数据缺失的处理方法有多种，常规分析多将未观测到的结果看作是二分类结果中的任一种结局（如视为吸烟），这样不仅“保守”，且显然不符合逻辑。“前面观测结果决定终观察结果”的LOCF分析，在OR值大于3时，更易得出差别有统计学意义的结论；考虑前观测结果对后干预效果的关联性时，随OR取值增大，更有可能得出差别有统计学意义的结果。若仅考虑个体变异，只模拟单个数据集进行缺失数据分析，在OR取值不同的情况下，均可见统计结果不稳定。当考虑个体、抽样和多重填补变异，采用多重填补其分析结果解释更符合实际。因此推知，考虑个体变异、样本变化的多重填补方法是以上四种方法中值得推崇的缺失数据分析方法。

高血压知行干预后吸烟缺失多是因受试者主观因素造成的，其数据缺失个体大多是干预后仍处于吸烟状态，因此认为吸烟与数据缺失间的假设是合理的。通过OR取值为1、3、5、7的多重填补100次模拟证实，随OR取值增大，更易得出差别有统计学意义的结论，即可认为该数据缺失与OR取值有关联。而考虑个体、抽样和多重填补变异时，当吸烟优势比较大（OR取值大于5），才有可能得出两区干预效果差别有统计学意义的结论，分析结果更具说服力，结论更稳健。

总之，单一终点二分类数据缺失，考虑个体、抽样和填补差异的影响进行多重填补是二分类缺失数据分析值得推崇的一种方法。本方法类似于加权估计方程处理缺失数据［6-7］的原理，利用已观测到的信息对缺失数据赋予合理权重，进而进行填补；考虑前次观测情况以及优势比OR取值的影响，对干预后单时点干预效果进行评价的影响是值得关注的。有关考虑个体、抽样和多重填补差异的多时点干预效果评价中结构数据缺失的分析方法研究有待进一步探讨。

1.Abraham W.T.，Russell D.W.M issing data：a review of currentmethods and applications in epidemiological research.Curr Opin Psychiatry，2004，17：315-321.

2.Siddiqui O，Hung HM.MMRM vs.LOCF：a comprehensive comparison based on simulation study and 25 NDA datasets.JBiopharm Stat，2009，19：227.

3.Donald H，Robin J，Hakan D.Analysis of binary outcomes w ith m issing data：m issing＝smoking，last observation carried forward，and a little multiple imputation.Methods and techniques，2007，10：1565-1569.

4.Long JS.Regression Models for Categorical and Lim ited Dependent Variables.Thousand Oaks，CA：Sage Publications，1997：42.

5.Little RJA，Rubin DB.Statistical Analysis w ith M issing Data，2nd edn.New York：Wiley，2002.

6.张伟，冯萍，赵永红.加权估计方程用于缺失数据的处理.中国卫生统计，2013，30（3）：435-437.

7.帅平，李晓松，周晓华.缺失数据统计处理方法的研究进展.中国卫生统计，2013，30（1）：137.

（责任编辑：郭海强）

The M ultiple Im putation and App lication in Binary LongitudinalM issing Data

Zhang Yao，Chen Peicui，Zhang Cuixian，et al（DepartmentofHealthStatistics，SchoolofPublicHealth，ShanxiMedicalUniversity（030001），Taiyuan）

ObjectiveTo clarify the basic principles of themultiple imputation（M I），wew ill introduce severalmethods w ith examples.MethodsCompare the analysis of four M Imodel，i.e.（1）simple M I.（2）Stratified M I.（3）The M Iwhich consider individual differences.（4）Perform the comprehensive analysis considering the individual，sampling and imputation.Carry outsensitivity analysis under different imputation sample，using SAS 9.2 to complete M I.ResultsLarge sample（N＝10000）simulation show that：simple multiple imputation analysis w ill reduce the ability of performance test，it can not response the difference between two samples.themultiple imputation analysis which considering the previous information w ill expand type I error.If only considerate the individual variability and simulate a data set，the conclude w ill be not stable；considerate the individual variability，sampling，and filling difference，whenOR≈2，the statistics result are close to the true value.We finally still can not believe that the rate of smoking are unequal between the two areas though the example of hypertension awareness intervention.ConclusionWhen we regard them issing as the event，therew ill increase the probability of type Ierror.When we consider the difference of individual，sampling and multiple imputation，we w ill draw amore robust parameter estimation.

M I；Longitudinal study；Binary m issing data；Evaluation

*：国家自然科学基金项目（编号81172774）；国家青年科学基金项目资助（81001294）；太原市大学生创新创业专题（120164023）

△通信作者：刘桂芬，E-mail：liugf66＠126.com