基于增长特征法与ARIMA的人均卫生事业费趋势预测比较研究*
潍坊医学院公共卫生学院(261053) 李望晨
基于增长特征法与ARIMA的人均卫生事业费趋势预测比较研究*
潍坊医学院公共卫生学院(261053) 李望晨
目的以增长特征法与ARIMA法对人均卫生事业费建立预测模型,比较方法原理、应用条件、数据要求、设计步骤和适配性能。方法依据算例资料,方法借助excel、SAS软件进行计算、检验和仿真实现;建立拟合模型并外推预测。结果两种方法均对卫生事业费增长趋势预测有代表性,前者强调截取近期部分数据优选曲线,适于近期规律最优曲线拟合,后者需数据充分和趋势差分处理,适于长期规律拟合,经建模比较ARIMA法更适于卫生事业费拟合,预测精度高。结论两种方法原理、前提条件、数据要求及和适配特点有差异;增长特征法特定于近期平滑增长趋势数据问题,适配好但不具更普遍的最优性能;ARIMA法对长期平滑趋势数据资料拟合预测好,对随机性时序资料有较强普适性;预测建模问题须注重原理分析、方法优选、数据处理和适配论证工作。
增长特征法 ARIMA 人均卫生事业费预测 比较研究
人均卫生事业费是指国家用于疾病防治、防疫和监控而保证公民身体健康的全部人均经费支出。改革开放后逐年稳定增长,影响或构成因素复杂,定量模型有助于拟合演化规律并推测未来费用到位情况,提供决策依据。根据时间序列预测思想,如果假设长期事物综合影响因素稳定变化且共同作用于未来发展,可根据数理统计方法由其随时间变化资料建立拟合模型进行外推预测。本文注重于两类方法套系建模设计,多层面分析讨论和实证比较应用意义。
基本原理
1.增长特征法[1]增长特征法是趋势外推理论的集成或延伸,假定事物随时间呈升降趋势且无较大波动,用于优化设计曲线类型的一套方法体系。它适合于平稳增长趋势变化的短期预测问题,以函数曲线拟合历史数据发展规律,经序列计算与曲线理论性质比较,优选曲线类型。
考虑对序列yt(t为时序)一阶差分ut=yt-yt-1,平滑预处理以消除随机干扰(不可过度削弱信息)。以代替yt,以代替ut,计算序列增长特征,与几种趋势曲线的理论增长性质进行比较,以二者相近为优选准则。记a,b,k为参数,曲线理论性质和序列增长特征匹配对照见表1。

表1 序列增长特征与几种曲线理论性质对照
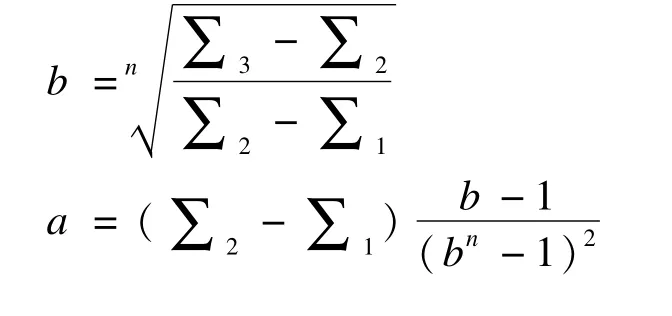
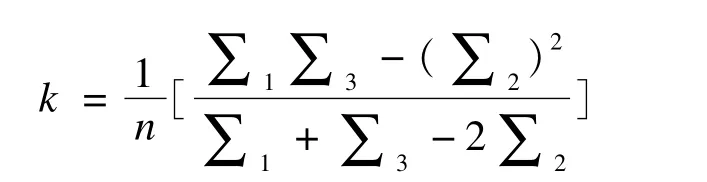
同理,若取对数序列lny0,…,lnyn-1;lnyn,…,lny2n-1;lny2n,…,lny3n-1,以及取倒数序列1/y0,…,1/yn-1;1/yn,…,1/y2n-1;1/y2n,…,1/y3n-1,等分三段求和,据此也可以推导后两种类型曲线参数公式。根据所建立模型可将t+1代入进一步外推预测yt+1数值。
2.ARIMA法 ARIMA(p,d,q)模型[2]即差分自回归移动平均模型(autoregressive integrated moving average,ARIMA),主要用于随机平稳时间序列拟合建模和外推预测,由Box和Jenkins提出,p,q为自回归和移动平均阶数,d为差分次数。记φi,θj分别为自回归和移动平均参数,原始序列{xt},残差序列{εt},延迟算子Bxt=xt-1;则模型式:

先对原始序列{xt}(不要太少)进行纯随机检验和平稳性检验确定其是否非纯随机平稳序列,若为白噪声序列则无须建模分析,若非平稳要经差分变换处理为平稳序列。计算样本自相关系数(ACF)和偏自相关系数(PACF),绘制样本时序图、自相关图和偏自相关图,并根据AIC、SBC准则判定拟合优度,进行定阶与优选,再估计参数建立模型。经{εt}白噪声检验以判断信息是否提取充分,将识别模型用于外推预测。ARIMA法步骤复杂,可借助SAS编程实现,迄今已成为时间序列建模经典方法。
实证分析
资料源自《中国卫生统计年鉴》1978-2009年我国人均卫生事业费统计数据。
1.增长特征法预测建模设计 增长特征法旨在根据时序资料匹配最优拟合曲线,适合数据稳定且平滑变化趋势问题(但也受此条件限制),该法不需太多数据而以近期数据反映演化规律,全部数据纳入会造成过度拟合历史规律。参数识别时需将数据等分三段,近期数据反映短期发展趋势,数据太多却会降低近期拟合与外推效果,数据太少则信息不充分,鉴于此考虑选用1998-2009年共12个数据。借助excel计算序列数值,见表2。
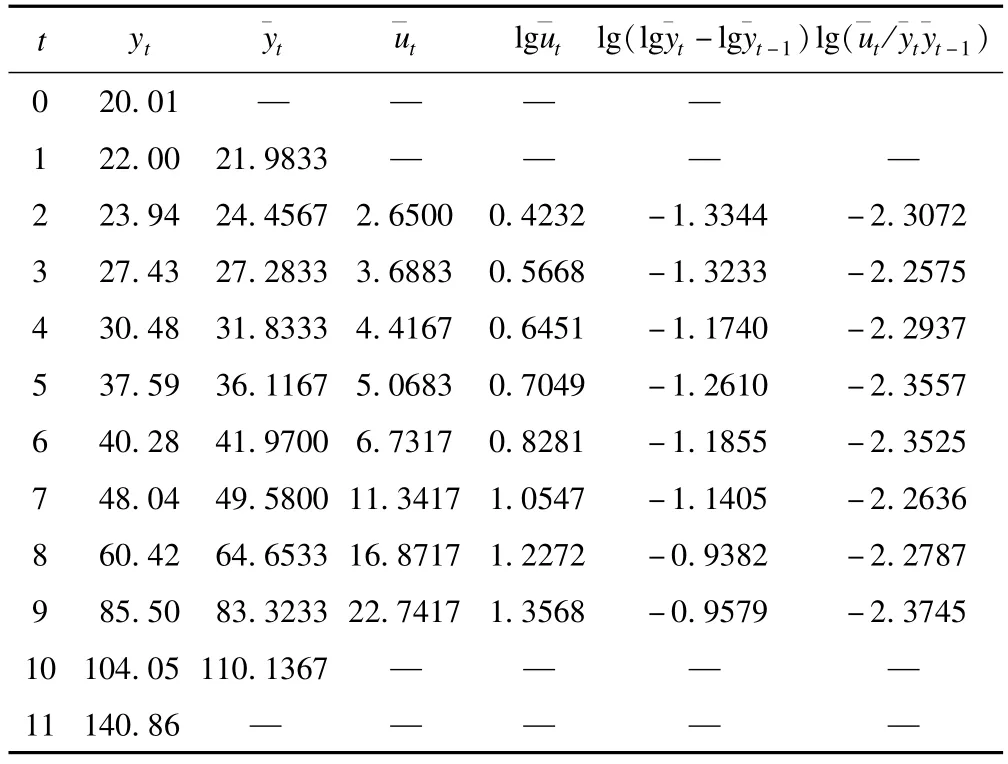
表2 各增长特征序列计算结果
2.ARIMA法预测建模设计 ARIMA法常用于拟合随机序列规律与建模[3-4],数据要求不能太少,将改革开放以来人均卫生事业费共32年数据全部纳入建模过程。借助SAS软件实现操作,经纯随机性检验认为序列相关有统计学意义(P=0.0238)。二阶差分序列、自相关系数(ACF)和偏自相关系数(PACF)依次由SAS软件给出,见图1。
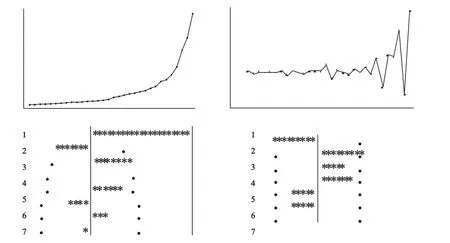
图1 原始序列、二阶差分序列、ACF和PACF依次简示
经分析,原始序列为非平稳序列,有明显递增趋势但无周期波动,经二阶差分为平稳序列。由图知ACF二阶截尾、PACF拖尾,根据AIC、SBC准则最优确定二阶移动平均模型MA(2)。根据参数公式识别模型ARIMA(0,2,2):(1-B)2xt=(1-0.66821B+B2)εt。
残差序列{εt}经白噪声检验,分别延迟12,18,24阶得P值为0.943,0.995,0.999>0.05,说明无任何信息可再提取,该模型拟合优度好。计算短期预测值和95%置信区间,2010年174.26[167.64,180.89],2011年209.2137[198.2018,220.225]。SAS程序如下:


3.结果比较 两套理论方法以不同原理和数据条件设计模型,拟合效果均非常好;前者拟合近期数据指数曲线的变化趋势,并严格将其假设以曲线外推;后者允许数据随机波动性特点,全部数据用于拟合整体历史规律,预测精度高一些。两套方法的建模表达式、预测值、相对误差见表3,拟合效果见图2~3。

表3 两套方法建模及预测结果比较
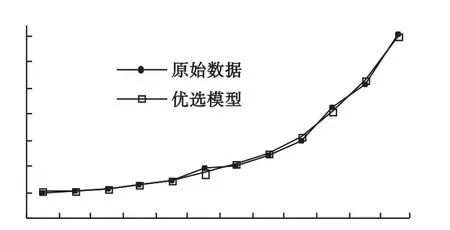
图2 指数曲线近期拟合简示图
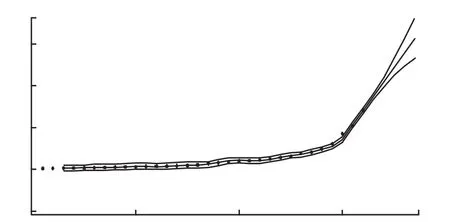
图3 ARIMA整体拟合简示图
讨 论
1.时间序列预测为定量技术研究范畴,以适配方法根据实际问题的时间变化资料建立模型,用于历史规律拟合和未来外推预测。我国人均卫生事业费统计数据连贯、资料无缺失,这类问题具有随时间稳定增长的特点,增长特征法和ARIMA法均可用于此类问题建模设计。二者方法原理、数据要求、限制条件、建模程序、设计过程和预测效果不同,应作适配论证,考虑近期数据段截取和去趋势差分预处理,然后比较研究方法应用价值。
2.增长特征法适于趋势性数据,更适于预处理后趋势稳定且近似呈曲线变化的问题,结合多技术优选曲线用于时序拟合、预测;数据不应太多应作近期数据段截取。本例拟合很好但因以近期曲线趋势为规律反映,以曲线刚性变化反映事物发展规律,不容许转折性存在,对特定平滑增长趋势问题拟合外推较好,对预测问题普遍意义和适配广度差一些。局限是近期平滑趋势数据建模,特定问题时适配好但不具普遍意义。
3.ARIMA是经典的时间序列方法,包括纯随机性与平稳性检验、差分运算、模型识别和残差检验等许多步骤,需要连贯而充分的数据(若数据少且散乱可选灰色方法),必要时经差分运算为平稳序列,拟合模型可以刻画转折性,对于随机波动性、周期性变化及复杂演化规律问题常有普适性和方法替代性。本例来看长期历史规律拟合效果好,外推预测误差小,不仅适于平稳增长趋势数据资料拟合,而且适合随机非平稳序列问题。适合卫生领域中时序性数据资料问题定量分析。预测方法均须经原理分析、数据处理和适配论证。ARIMA法适于卫生事业费等平滑增长趋势预测,对长期趋势数据资料拟合预测具有普适性,可推广于卫生预测领域。
1.秦侠.卫生管理运筹学.北京:人民卫生出版社,2005,80-120.
2.王燕.应用时间序列分析.北京:中国人民大学出版社,2008,1-100.
3.孟蕾,王玉明.ARIMA模型在肺结核发病预测中的应用.中国卫生统计,2010,27(5):507-509.
4.李红,潘东峰,郭忠琴,等.时间序列模型在医院感染发生率拟合预测中的比较研究.中国卫生统计,2013,30(1):87-89.
(责任编辑:郭海强)
*:山东省自然基金ZR2013HM 045;山东省社科规划项目11CGLZ09;潍纺市科技局项目201301079;全国统计科研项目2013666

