电能计量设备自动检定流水线调度优化研究
方彦军,唐 猛
(武汉大学 自动化系,武汉 430072)
随着“集中检验、统一配送”的电能计量装置管理模式的推广,近年来,多个省级电力公司都相继建立了各自的省级计量检定中心。同时,电力需求侧管理现代化发展水平的不断提高,也对电能计量装置的管理、检定的效率提出了更高要求。电能计量设备自动检定流水线是一种现代化电能表检定装置,能够实现电能表检定过程的全程自动化。因此,如何提高自动检定流水线的检定效率,已成为目前各省级计量检定中心亟待解决的难题。
为提高检定效率,需将不同批次、相同电压等级的计量装置放在一条流水线上进行检定,这就对检定流水线的调度提出了更高要求。对于该类混合流水线调度问题HFSP(hybrid flow-shop scheduling problem),文献[1-6]均进行了深入研究。本文针对其特点,设计了一种包含检定排序和设备选择信息的编码和解码方法,将遗传算法得到的精英解作为禁忌算法的初始解,并运用“高”邻域候选集策略,来提高遗传禁忌混合算法的寻优能力。
1 自动检定流水线调度问题数学模型
1.1 问题描述
为了提高智能计量设备自动检定流水线的效率,生产调度中心会依据用户需求、智能立库存储量及检定周期等因素,将不同批次的同类型计量器具(单相电能表)或相同电压等级的不同类型器具(单相电能表和终端)放在一条流水线上进行检定。同时,在至少一个检定环节(如:多功能检定环节)中存在多条独立的并行检定单元,且每个检定单元含有多个检定工位,可实现多批次、多计量设备的同时检测。因此需要将待检器具进行分批组处理,每个批组的大小也可不同。
根据上述分析,本文将此类自动检定流水线定义为带批组的并行混合流水线[17-19]。带批组并行混合流水线调度问题可描述为:n个计量器具分为B个批组在流水线上进行S个环节的检测,各环节至少有一台检定设备且至少有一个环节存在并行的检定设备,同一环节中各检定设备检测同一计量器具的检测时间均相同[11],每个批组在同一环节的检测时间不完全相同,在每一环节各待检器具均要完成一道工序,但各待检器具的每道工序可在相应环节中的任意并行检定设备上检定,已知待检器具各道工序的检定时间,要求确定所有待检批组的排序以及每一环节中并行检定设备的任务分配情况,从而使得总检定完成时间最小,即最小化最大检定时间,图1为自动检定流水线流程图。
1.2 数学模型
令 Ji为待检器具的编号,i={1,2,……,n},其中n为待检器具总数;bL为第L批组中的待检器具数量,L={1,2,……,B},其中 B 为待检器具的批组总表示批组 L 中的第 f个待检器具,f={1,2,……,bL},aL,f与 Ji是一一对应的;md为检定环节 d 中的并行设备数,d={1,2,……,S},其中 S 为环节总数;td,L为批组 L 在环节 d 的检测时间;Sd,L为批组L在环节d的检测开始时间;ed,L为批组L在环节d的检测结束时间;CL为批组L的检定完成时间;Cmax=max{C1,C2,……,CB}为所有批组检定完成的最大时间;则具体的数学模型为

其中:式(1)为调度优化指标;式(2)表示每个优先级位置只能对应一个批组;式(3)表示每个批组只能占有一个优先级位置;式(4)表示每个环节每个批组只能在一台检定设备上进行检测;式(5)表示同一环节检测开始时间与完成时间的关系;式(6)表示同一批组在不同环节间的先后约束关系;式(9)表示同一环节排位越前的批组开始检测的时间越早;式(10)表示同一环节分配在同一设备上的不同批组,优先级靠前的批组检测完后才允许后面的批组进行检测。
2 基于GATS算法的自动检定流水线调度
2.1 遗传禁忌混合算法
遗传算法是通过将具体问题的求解抽象成生物“染色体”种群的一代代进化,包括选择、交叉和变异等操作,最终找到“最适应环境”的最优个体,从而完成对问题最优解的自适应搜索。该算法的大范围搜索能力较强,但局部搜索能力较差[13]。
禁忌搜索TS(tabu search)算法具有灵活的记忆功能,在搜索过程中可以接受劣解,从而跳出局部最优解,具有很强的局部搜索能力,但该算法对于初始解的依赖性较强[14]。将遗传算法与具有记忆功能和较强“爬山”能力的禁忌算法混合使用,一方面能够提高禁忌算法搜索效率,同时又能克服GA爬坡能力弱的缺点[7]。为了结合两种算法的各自优势,本文采用一种改进的遗传禁忌算法,并运用多精英策略[8-9],即选取适应度排位靠前的精英解与非精英解进行交叉操作。对遗传操作得到的解集进行重新排位,选取适应度排位靠前的精英解作为禁忌操作的初始解,并利用禁忌搜索中得到的最优解对初始解进行替代更新,直至满足一定条件跳出算法得到最优解。算法流程如图2所示。

图2 改进的遗传-禁忌混合算法流程Fig.2 Procedure of improved GATS algorithm
2.2 编码与解码
待检器具的批组总数为B,则令染色体长度为B,编码矩阵 AS*B构成一个染色体,见式(11),表示一共B个批组需要经过S个检定阶段,至少一个阶段存在md台并行检定设备,每个染色体与解集是一一对应的。 其中矩阵中的元素 ad,L为区间(1,1+md)的一个随机实数,表示批组L的第d个检定阶段在第 Int(ad,L)台并行设备上进行检定,染色体中包含了各个批组在不同检定阶段的检定顺序及设备选择信息。例如,个体[a1,1,a1,2,a1,3……]=[1.1,1.3,1.2……],1.3表示批组2的第一个阶段在设备1上进行检定,小数位“3”表示在同一阶段选择同一设备的批组检定顺序,所有待检批组的序号在个体中的位置表示各批组的检定排序,因此基因在染色体中的相对位置直接反映出各批组的检定顺序。根据1.2节所述的约束条件确定同时包含各批组检定排序和各阶段并行检定设备的任务分配策略即称为解码。

对于确定待检批组的检定排序,即为确定不同批组在相同阶段的检定开始时间排序。本文采用以下策略:按照先到先服务FCFS(first come first service)的方式确定检定排序,即前阶段先完成的批组先进行下一阶段的检定。若多个批组在该阶段并行设备上的检定完成时间相同,则仍然按照前一阶段的排序进行后续阶段的检定。对于并行检定设备的分配问题,采用最先闲置机器原则[4]:
1)根据各批组在前一阶段的检定顺序,依次计算每个批组在下一阶段第k台并行检定设备上的最早允许检定时间 Pd,L,k=max(Cd-1,L;rk),其中 rk为并行设备k的最先空闲时间。
2)计算下一阶段各并行设备的优先系数aL,k=max(Cd-1,L;rk)+td,L,选择优先系数值最小的设备作为其在该阶段的检定设备,并更新批组L在阶段d的检定完成时间Cd,L和设备k的最先空闲时间rk。
2.3 种群初始化
为了使初始解保持一定的分散性,本文采用随机方法产生初始化解 Si,i=1,2,…Psize。
2.4 适应度函数与选择
本文的优化目标为所有待检批组的最大完成时间,为了避免算法出现早熟和随机漫游现象,采用乘幂变换对目标函数进行适度缩小,则适应度函数为
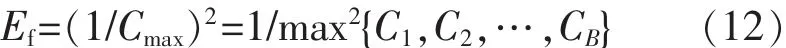
式中,Cmax(Q)为第Q个染色体所代表的一个调度方案的最大检定周期。选取每代中适应度值排位在前ω的精英解采用最佳个体保存法,即直接复制到下一代,对其余解按照轮盘赌法进行选择。
2.5 交叉和变异
将适应度值排在前列的精英解与非精英解进行随机的自适应单点交叉操作[9],并验证交叉后得到的解是否满足所有约束条件。具体算法如下:
1)选取一个随机概率大于预设交叉概率的非精英解与一随机精英解进行交叉操作,并对交叉后的解进行有效性验证,包括验证其是否满足上述所有约束条件;
2)将交叉后的子代与非精英父代的适应度值进行对比,若子代的适应度值优于父代,则子代个体自动取代非精英父代个体进入下一代种群;否则仍然保留父代个体。
本文采用一种混合变异算子[10],若当前种群的目标函数最大值与最小值之差小于某一正数时,采用高斯变异,否则采用边界变异。因此,在进化初期采用边界变异,即首先选取不同类型的批组所在的基因位作为变异点,然后用两者对应的边界基因之一替代原有基因值;后期主要进行高斯变异来提升算法对重点区域的搜索能力。
2.6 禁忌搜索
2.6.1 邻域结构及候选集
本文首先采用交换邻域结构:任意选择同一检定设备上的两个批组,交换其检定顺序。其次,采用“高”候选集策略产生候选集[15],即:将总检定完成时间最大的并行机上任意批组插入到总检定时间最小的并行机上任一批组前。
2.6.2 禁忌表的设计
禁忌表采用先进先出的队列来实现。在禁忌搜索过程中,会出现当前解的领域全部被禁忌,或是某一解被禁忌后当前最优值将下降的情况,为了避免搜索算法丢失优化状态实现全局最优,本文基于特赦规则:根据解的适应度值,若出现某个候选解的适应度值优于当前最优解时,虽然从当前最优解到该解的变化被禁忌,但可以解禁该候选解作为当前最优解[12]。
2.6.3 关于精英解的禁忌算法
禁忌算法的终止规则选用目标控制原则:当前已存在的最优解的适应度值连续nt次大于之后搜索到的解适应度值,则停止搜索[16]。禁忌搜索算法流程如图3所示。
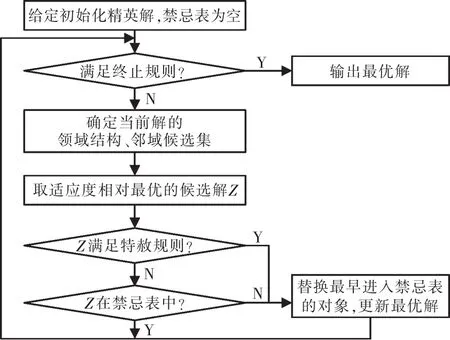
图3 TS算法流程Fig.3 Flow chart of TS algorithm
3 实例
某省级电能计量设备自动检定中心对一批含有9个不同批组的电能计量设备进行检定。每个批组都要经过外观、耐压检测环节,多功能检测环节,分拣、封印及自动贴标签环节等3大环节共6个单元的检定。其中在多功能检测环节有3组并行且独立的U型检测工位,每个工位含有60个表位可同时进行检测,即 BL≤60,B∈(0,6),但是不同批组在每个环节的检定时间不尽相同,具体检定时间如表1所示。
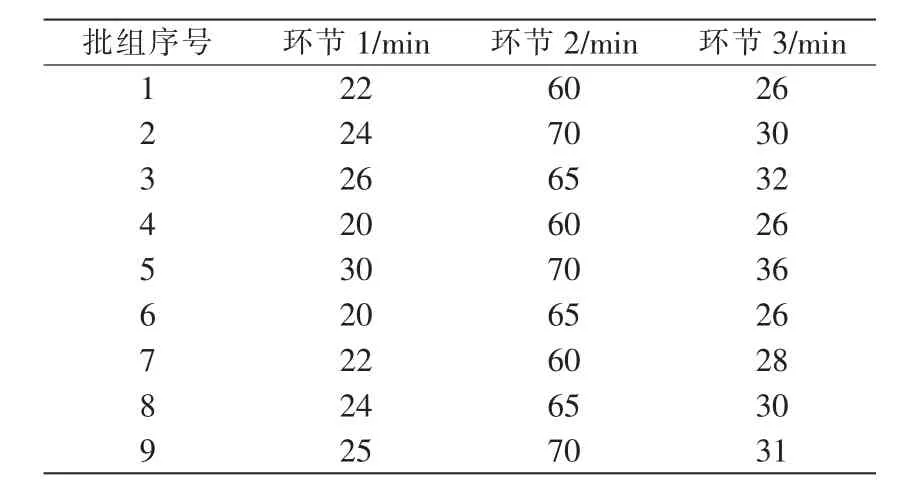
表1 检定时间Tab.1 Verification time of the instance
运用Matlab编程来实现本文算法,混合算法参数设置如下:遗传种群数量为80,交叉概率为0.9,变异概率为0.1,精英保留率取ω=20%,遗传算法最大进化代数为200,禁忌邻域解个数为10,候选解的个数为8,禁忌表长度为8,禁忌终止条件为连续nt=8次无法找到适应度值更优的解。
为更好地验证该混合算法具有收敛快、优化率高的特性,以实例为背景,将本文提出的IGATS与ABC[1]、TS[4]、PSO[6]进行比较。 表 2 为每种算法获得最好解的10次独立运行结果的平均值。

表2 实例的4种优化算法比较Tab.2 Result comparision of four optimization algorithms under the instance
从表2中可看出,本文提出的IGATS算法经过大概80次就趋于收敛,与其它3种优化算法相比,收敛速度较快,计算时间较短,且最优检定完成时间为346 min,因此能够寻到另外3种算法找不到的最优解,四种算法在寻优成功率方面的表现相当。综上所述,该遗传禁忌算法的搜索空间能力较强,并具有快速求出最好解的特性,综合性能优于其它3种算法,能够为检定流水线的优化调度提供更多的理论依据。IGATS算法的最优解甘特图如图4所示。其中:横坐标为各批组在该阶段所需时间;纵坐标为批组在该阶段所选择的机器编号,如:机器2对应的 “1-2”表示批组1的第2个阶段在设备2上进行检定,方格长度代表所需时间的长短。
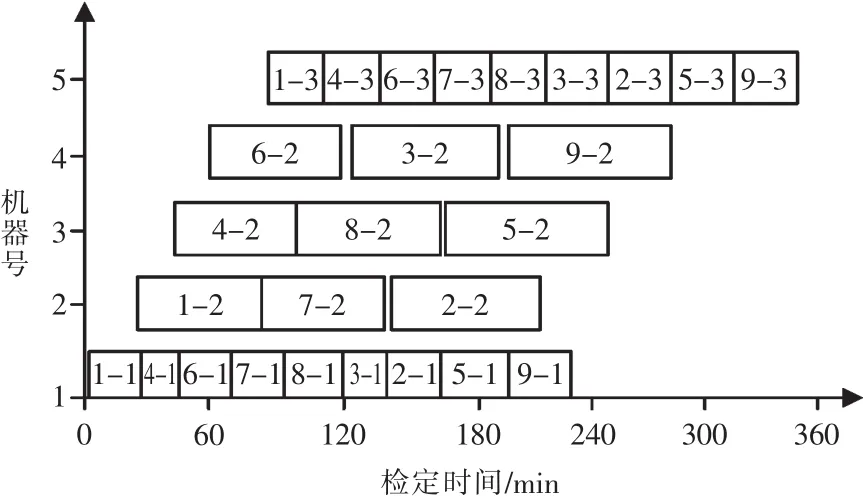
图4 IGATS算法的最优解甘特图Fig.4 Gantt chat of the optimal solution
4 结语
针对电能计量设备自动检定流水线调度问题,本文提出一种有效的遗传禁忌混合算法:设计了一种包含检定排序和设备选择信息的编码和解码方法,将遗传算法得到的精英解作为禁忌算法的初始解,并运用“高”邻域候选集策略,来提高混合算法的寻优能力。以某省级检定中心自动检定流水线为背景,将该算法与另外3种优化算法进行比较,表明该算法收敛速度更快、优化率更高,得到的解最优,具有较强的有效性和鲁棒性。
[1] 王凌,周刚,许晔,等.求解不相关并行混合流水线调度问题的人工蜂群算法[J].控制理论与应用,2012,29(12):1551-1557.
[2] PAN Q K,TASGETIREN M F,SUGANTHAN P N,et al.A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J].Information Sciences,2010,181(12):2455-2468.
[3] 王圣尧,王凌,许晔.求解相同并行机混合流水线车间调度问题的分布估计算法[J].计算机集成制造系统,2013,12(6):51-15.
[4] WANG X,TANG L.A tabu search heuristic for the hybrid flow-shop scheduling with finite intermediate buffers[J].Computers&Operations Research,2008,36(3):907-918.
[5]ALAYKYRAN K,ENGIN O,DOYEN A.Using ant colony optimization to solve hybrid flow shop scheduling problem[J].InternationalJournalofAdvanced Manufacturing Tech-nology,2007,35(5/6):541-550.
[6] TSENG C T,LIAO C J.A particle swarm optimization algorithm for hybrid flow-shop scheduling with multiprocess-or tasks[J].International Journal of Production Research,2008,46(17):4655-4670.
[7] 姚静,方彦军,陈广.遗传和禁忌混合算法在机组负荷分配中的应用[J].中国电机工程学报,2010,30(26):95-99.
[8] 朱灿,梁昔明.一种多精英保存策略的遗传算法[J].计算机应用,2008,28(4):929-931.
[9] 刘爱军,杨育,邢青松,等.复杂制造环境下的改进非支配排序遗传算法[J].计算机集成制造系统,2012,18(11):446-458.
[10]吕潇,孙跃.复合谐振感应电能传输系统分析及参数优化[J].电力系统自动化,2013,37(4):119-124.
[11]ZHANG C S,OUYANG D T,NING J X.An artificial bee colony approach for clustering[J].Expen Systems with Applications,2010,37(7):4761-4767.
[12]陈铁梅,罗家祥.带扰动和变异因子的改进禁忌搜索算法求解贴片机过程优化[J].控制与决策,2013,28(3):363-368.
[13]ALFIERI A.Workload simulation and optimization in multicriteria hybrid flow-shop scheduling:A case study[J].International of Production Research,2009,47(18):29-45.
[14]ORTMANN M C,VIGNIER A,DARDILHAC D,et al.Branch and bound crossed with GA to solve hybrid flow-shops[J].Europe Journal of Operational Research,1998,107(2):389-400.
[15]Chiang C L.Genetic algorithms for power economic[J].IET on Generation Transmission and Distribution,2007,11(2):261-269.
[16]苏凯,刘吉臻,牛玉广.考虑直吹式钢球磨电耗的厂级负荷优化分配[J].中国电机工程学报,2012,32(2):24-30.
[17]XU Y,WANG L.Differential evolution algorithm for hybrid flow-shop scheduling problem[J].Journal of Systems Engineering and Electronics,2011,22(5):794-798.
[18]王凌,周刚,许烨,等.混合流水线调度研究进展[J].化工自动化及仪表,2011,38(1):1-8.
[19]王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003.■

