基于ARMAX模型的集中供热系统负荷预测研究
魏延宝,林红权,马增良,王学雷
(中国科学院自动化研究所,北京100190)
近年来集中供热的规模不断扩大,用户对供热质量的要求也不断提高,实现按需供热、均匀供热成为亟待解决的关键问题[1]。集中供热系统中各自动控制子系统的给定值都是由预报负荷决定的,因此实现及时准确的负荷预测是提高供热质量的前提和基础。对于制定能源规划、提高供热系统能源利用效率、保护环境具有重要意义[2]。
供热负荷是指在某一室外温度下,为达到要求的室内温度,供热系统在单位时间内向建筑物供给的热量[3]。由于供热系统内导热介质以及建筑物的热惯性、迟滞等特点,室外风速、太阳辐射、建筑物结构以及使用情况等因素影响也比较复杂,通过机理方法建立准确的负荷预测模型非常困难。近些年来,国内外专业人士针对这一问题也提出了许多解决方法,如回归预测和神经网络等。回归预测方法计算简单,但模型精度较低;神经网络方法尽管精度很高,但所需数据多且容易陷入局部极小,同时网络结构的确定有很强的主观性,因此并不令人满意[4-6]。本文采用时间序列分析方法,利用热负荷的历史数据,并充分考虑外界因素的影响,能够在短时间内建立预测模型并以较高的精度对未来时刻的热负荷进行预测。
ARMAX扩展自回归滑动平均模型(extended auto-regressive moving average)能够准确地描述动态过程,在电力系统以及计量经济等领域都有着广泛的应用[7]。利用ARMAX模型预测供热系统热负荷,通过对历史数据的统计和分析寻找热负荷的变化规律。本文对ARMAX模型进行了详细的介绍,并采用最小二乘法进行了参数估计。通过对热负荷数据进行统计和分析,得到了锅炉供水温度预测模型。经对比,预测结果在短期内具有较高的精度。
1 ARMAX模型介绍
当系统中某一因变量的时间序列数据没有确定的变化形式,也不能用时间的确定函数描述时,可以用概率统计的方法寻求比较合适的随机模型近似反映其变化规律。ARMAX模型是一种典型的描述离散时间序列的工具,其结构上由AR模型、MA 模型及回归项 3 部分结合构成。 (p,r,q)阶ARMAX模型的数学表达式如下:

其中:p、q、r分别是自回归、滑动平均以及回归项的阶数;θi(i=1…p)、φj(j=1…r)和 wk(k=1…q)是模型的待定系数;et是均值为零方差不为零的白噪声序列。模型输出yt为平稳的时间序列,ytyt-1…yt-m是该序列不同时刻的随机变量值,反映时间的滞后关系。B为一阶后移算子,满足:
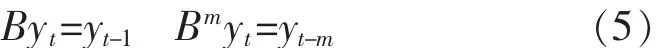
ARMAX模型融合了AR模型和MA模型的特点,通过对过去的观测值、现在的干扰值以及过去的干扰值线性组合进行预测。与传统的ARMA相比,通过引入与输出序列相关的另一序列作为回归项,模型的准确性及鲁棒性更高。利用ARMA模型解决问题的一般步骤如图1所示,核心环节是序列平稳化及模型参数的求取,将在下面的相应章节中作详细介绍。

图1 建立ARMAX模型流程图Fig.1 Flow chart of establishing ARMAX model
2 序列平稳性分析
进行时间序列模型估计,前提是满足序列是非随机且平稳的条件。若随机,序列的前后观察值之间无任何关系,则没有任何信息可以提取;若非平稳,即序列变化特征随时间推移而改变,这样即便找到变化规律,也无法用于预测。
随机性可以通过序列的自相关系数来判断,若存在非0,则证明该序列是非随机的,反之则为随机序列;平稳性的判断有多种方法,可以通过相关图法利用时间序列的相关图衰减特性进行判断,也可以通过单位根检验利用统计检验的方法进行判断。
对于非平稳序列,为了满足利用ARMAX模型建模的条件,可以进行d阶(d一般不超过2)差分使非平稳时间序列平稳化[8]。为此,首先定义一个差分算子Δ=1-B,满足:

这样就可以将非平稳序列转化为平稳序列再进行估计和建模。综合上述分析,得到了经差分后平稳的d阶ARMAX模型,结构如下:

集中供热系统根据被控变量的不同有不同的控制运行方式,如控制供回水差压为主的运行方式和控制供水温度为主的运行方式。已知中关村某供暖公司采用调节供水温度和运行时间的方式调节热负荷,指导司炉作业和供热运行,供水流量不作频繁调节。因此,本文针对这一控制供水温度为主的集中供热系统,将锅炉供水温度作为分析和预测的对象,根据SCADA系统采集到的2012年11月份的供水温度数据绘制出时序图,数据采集周期为每小时 1次,如图 2(a)所示。
通过对供热系统时序图的分析不难发现,供水温度的变化是非平稳过程,具有一定的增长趋势和周期性。经过分析,在对数据进行了一阶差分及平移处理后得到了一个平稳且非白噪声的时间序列,如图 2(b)所示。

图2 热负荷温度时间序列图Fig.2 Time series of load temperature
3 ARMAX模型参数求取
ARMAX模型参数的求取包含两方面内容,阶次的确定以及模型参数的估计。
3.1 模型阶次的确定
模型的阶次通过检验变量的自相关函数和偏相关函数来确定。按照定义,列出时间序列yt(t=1…N)的统计特性参数如下:
均值μy和方差σy2分别为
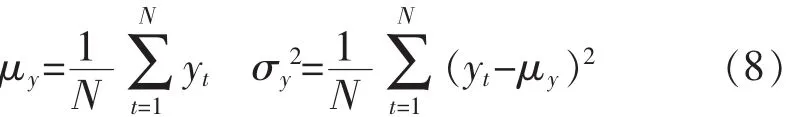
由此,得到协方差 Cov(yt,yt+k)和自相关函数 ρk:

偏相关函数Φ的定义为
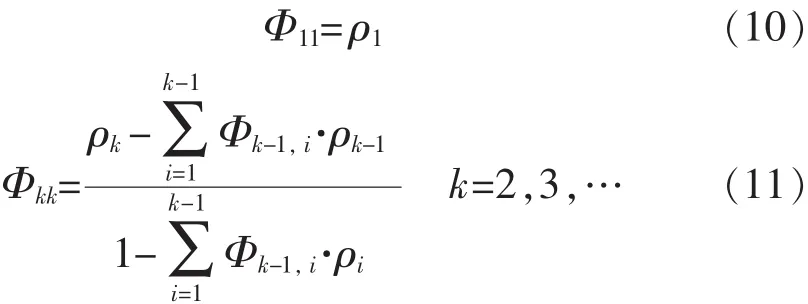
Φk,i=Φk-1,i-Φkk·Φk-1,k-ik=1,2,3,…k-1 (12)
对于AR模型,序列满足偏相关函数滞后期截尾这一特性。即对于p阶的AR模型,自相关函数满足:

所以当求出使偏自相关系数为0时的k值,可以得到模型的自回归阶次k-1。
而对于MA模型,自相关系数是截尾的,其性质和AR模型类似。对于q阶的MA模型,当得到自相关系数为0时的k值,可以确定MA模型的阶次为k-1。根据以上对于AR和MA模型的特性分析,可以大致得到p和q的数值,关于输入阶次r的确定,应本着灵活性和节俭性的原则,既要满足模型通用性又不至于使运算过于复杂[9]。
3.2 模型参数的估计
线性回归模型参数估计最常用的方法是最小二乘法,可以按下面的方式进行数学描述。
当数学模型有下面的形式时:

式中:y(p)为模型拟合变量;x1(p),x2(p),…,xN(p)为影响预测结果的因变量;β1,β2, …,βN为回归参数;N 为模型阶次;M为样本的个数。模型的残差为
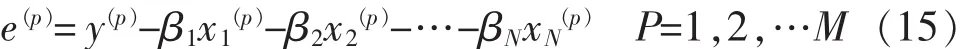
假设:

最小二乘法估计就是寻找参数估计值 β1′,β2′,…,βN′,使误差平方和最小,即按如下目标函数进行优化:
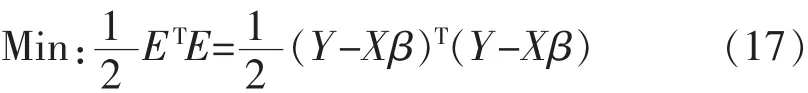
对上式求导,得到最小二乘估计的解为

3.3 负荷温度模型参数求取
经过平稳化后的负荷温度时间序列,其相关图如图3所示,通过观察其相关图的拖尾性可以大致确定该序列的ARMAX结构,其自回归及滑动平均的阶次为3和5,初步考虑可以采用ARMAX(3,2,5)结构。

图3 供水温度时间序列相关图Fig.3 Correlogram of supply water temperature series
根据以上确定的模型阶次,获得了一系列的模型结构。此时,需要根据AIC和SC参数最小的原则进行最优模型选择[10]。经过结果比较,最终选择的模型为 ARMAX(3,2,4)。借助于计算机仿真软件进行参数辨识和最优选择,得到的最终模型如下:
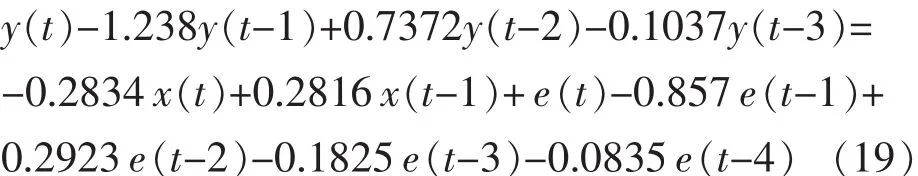
4 模型检验和热负荷预测
在对数据进行建模过程中,要检验模型的适用性,模型适用才能输出模型。模型检验的实质是对模型残差序列进行白噪声检验[11-12]。若残差序列非白噪声,说明一些重要信息没被提取,应重新设定模型。对残差进行纯随机性检验。对残差序列进行相关性分析,输入滞后阶数为14,得到如图4所示的相关图。

图4 残差序列相关图Fig.4 Correlogram of error series
通过相关图的分析不难看出,残差为白噪声,表示拟合模型有效。模型的拟合结果如图5所示。该图中的下半部分的空心圆连接线代表误差曲线,上半部分的粗实线代表实际的供水温度(经过一阶差分后的序列),叉号连接线代表利用模型获得的拟合值。
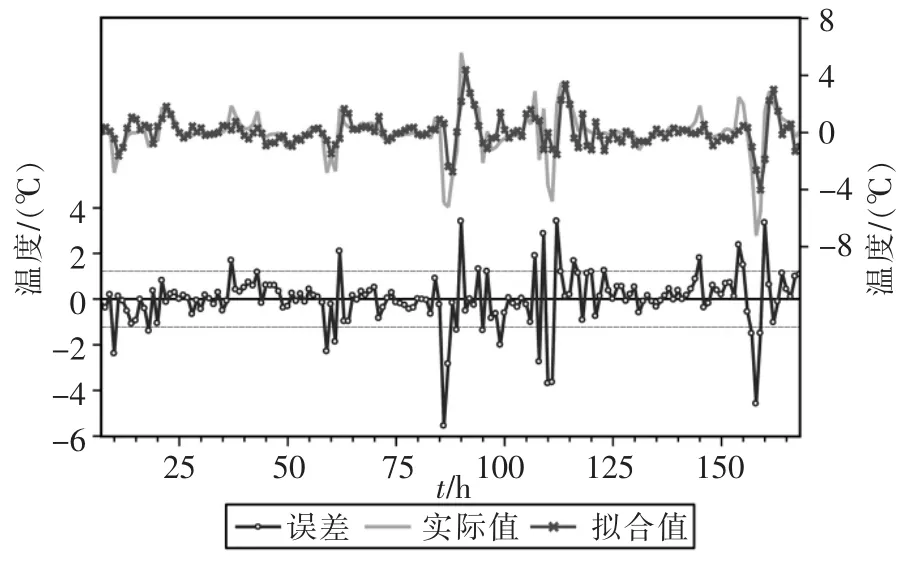
图 5 ARMAX(3,2,4)模型拟合图Fig.5 Fitting figure of ARMAX(3,2,4)
之后,按照已经建立的热负荷预测模型(19),对未来时刻的供水温度进行预测。为了验证模型的有效性,首先需要给出模型准确度评价标准。由于预测值和真实值之间的误差有正有负,因此采用MPAE(平均绝对百分比误差)来进行总体准确度评价。MPAE定义为

还有一个评价标准是最大误差百分比,是指在一定时间段内所有时刻的误差百分比中的最大值,记为MPE(最大百分比误差)。
对供水温度进行预测,并与实际运行值进行对比,得出预测模型的准确度。由于时间序列模型采用递推的方式进行,易得到下一小时的供水温度预测值,其他时刻负荷预测计算方法与此相似。最终得到了未来24 h供水温度预测表如表1所示。
经过计算,该模型的MPAE的值为2.6657%,MPE的值为4.9753%。通过与预期误差百分比相比较,即可对模型的预测精度进行评价。经过逐步递推,得到了未来72h的MPAE和MPE的值,如表2所示。
可见,当时间延长后,模型的准确度开始下降。平均误差百分比开始增大,并且最大误差百分比呈现很高的态势。因此,在做实际预测时必须结合容差考察模型的适用周期,在适用周期以外需要对模型参数重新计算和调整,使其满足精度要求。
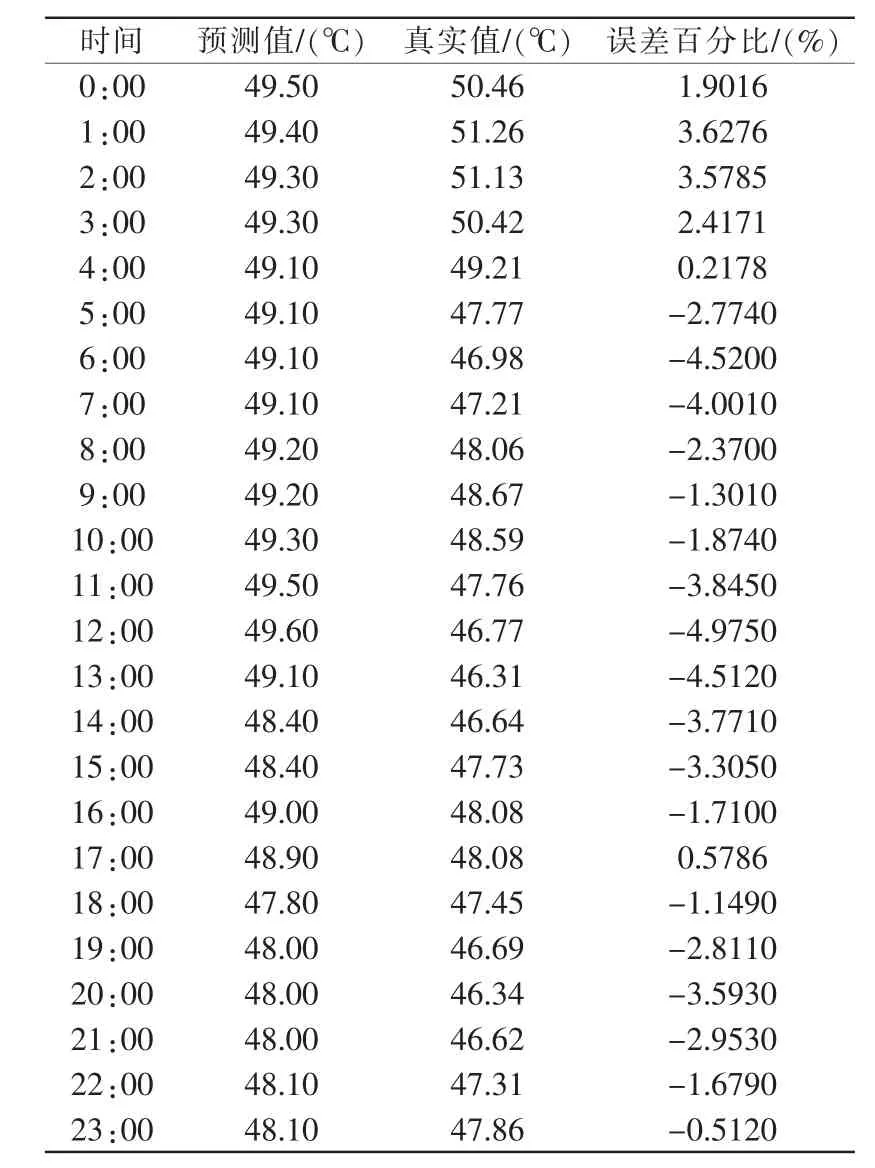
表1 24 h预测数值及误差大小Tab.1 24 hours predicted value and corresponding error

表2 未来72 h内的误差百分比Tab.2 Percentage error of the next 72 hours
5 结语
通过验证发现,利用ARMAX模型进行集中供热系统热负荷预测时,计算简单并且所需数据少,在一定的误差范围内是很有效的。短期预测准确度很高,但在进行长期预测时精度下降。通过对供热负荷进行分析建模实现准确预测,为负荷分配及优化调度提供数据支持,对于能源的合理规划和高效利用都具有重要意义。
[1] 石兆玉.供热系统运行调节与控制[M].北京:清华大学出版社,1994:135-160.
[2] 张艳.基于模糊神经网络的集中供热负荷预测[D].阜新:辽宁工程技术大学,2009,12:1-5.
[3] 朱学莉,齐维贵,陆亚俊.建筑供热负荷预报与预测控制策略研究[J].控制科学与决策,2002,11(17):703-706.
[4] 袁晓辉,王乘,张传勇.电力系统短期负荷预测方法的进展[J].电气自动化,2004,26(6):13-16.
[5] 李晋,秦琳琳,岳大志,等.试验温室温度系统建模与仿真[J].系统仿真学报,2008,20(7):1869-1875.
[6] 王东亚.基于自适应遗传人工神经网络的集中供热负荷预测和控制研究[D].阜新:辽宁工程技术大学,2005,11:4-6.
[7] 叶瑰昀,罗耀华,刘勇,等.基于ARMA模型的电力系统负荷预测方法研究[J].信息技术,2002(6):74-76.
[8] 张晓峒.计量经济学基础[M].天津:南开大学出版社,2007:282-335.
[9] 韩路跃,杜行检.基于Matlab的时间序列建模与预测[J].计算机仿真,2005,22(4):105-107.
[10]党红刚,马亮亮.基于ARIMAX模型的海西州地区高血压月发病率预测[J].中国老年学杂志,2011,11(31):4428-4430.
[11]刘严崴.基于神经网络的供热系统负荷预测[D].天津:天津大学,2009,08:33-34.
[12]万志宏.基于时间序列的电力系统短期负荷预测研究[D].广州:华南理工大学,2012,04:20-30. ■

