浅水航道舰船水压场理论解及其计算
孙帮碧,张志宏,刘巨斌,邓 辉
(海军工程大学理学院,湖北武汉 430033)
浅水航道舰船水压场理论解及其计算
孙帮碧,张志宏,刘巨斌,邓 辉
(海军工程大学理学院,湖北武汉 430033)
基于浅水波动势流理论,建立亚临界航速和线性跨临界航速浅水波动控制方程。基于薄船假定,利用傅里叶积分变换法获得浅水航道舰船水压场理论解。通过数值求解,分析舰船航速、水深、航道宽度、色散效应对舰船水压场特性的影响,并与源汇分布法计算结果进行对比,验证所建立的浅水航道舰船水压场数学模型和计算方法的正确性与有效性。
浅水;航道;舰船;水压场;理论解
0 引言
航行舰船引起的水底压力变化简称为舰船水压场。舰船水压场是舰船物理场的自身特性,是设计新型水雷及研制水压扫雷具以及舰艇自身防护的依据。Tuck[1]基于渐近匹配展开法,得到浅水薄船水压场的近似解;Muller[2]利用有限水深兴波源势方法,在船舶纵向剖面上布置源汇,给出薄船、线性自由表面条件下的舰船水压场计算公式;Sahin和Hyman,Nguyen[3-4]等采用有限水深格林函数方法,系统开展了潜艇、水面舰艇和气垫船水压场的理论建模和数值计算工作;Jiang[5]和 Gourlay[6-7]基于浅水波动势流理论对舰船兴波和升沉与纵倾作了分析与计算;黎昆[8]、缪涛[9]等利用面元法计算舰船在水底引起的压力分布。
1 控制方程
假设流体为理想不可压流体作无旋运动,舰船沿浅水航道中心线运动,船体两侧流场左右对称。如图1取动坐标系固结于船体,坐标原点位于船体水线中心,z轴垂直向上,船头指向x轴正方向,水深为h,自由表面起伏为ζ,船速恒为V。在动坐标系下水流相对于船体以速度V沿x轴负方向运动。

图1 坐标系Fig.1 Coordinate system
舰船运动引起的流场扰动速度势Φ应满足下列方程:

如果不考虑式(8)中第三项 (色散项),则式(8)蜕化为亚临界航速浅水控制方程 (SSW),即

2 理论模型
针对SSW和LTSW方程,结合船体边界条件以及岸壁条件即可求出满足相应条件的舰船水压场理论解。根据薄船假定,船体边界条件为

式中:S(x)是船体横截面面积分布,Sx(x)为S(x)对x求导。
采用数学船型,其横截面面积分布为

2.1 采用SSW方程
2.1.1 矩形航道
1)源汇分布法
为简便计,省略表示平均的符号 “—”。舰船以亚临界航速在浅水中航行时,速度势Φ应该满足控制方程式(9)、船体边界条件式(10)以及岸壁条件式(6)。通过源汇分布法易于求得速度势Φ,并根据拉格朗日积分求得舰船水压场水底压力系数为

根据流场对称性,取y>0。对船体边界条件式以及岸壁条件式进行傅离叶变换,得

2.2 采用LTSW方程
2.2.1 矩形航道
针对无量纲控制方程式(7),省略平均符号“—”和无量纲符号“*”,采用傅离叶积分变换法,分超临界航速和亚临界航速2种情况进行求解。

当k在-∞ ~∞间变化时,λ2存在大于和小于2种情况,需要分别讨论:
① 当 λ2>0时,类似超临界航速求解方法,有


如果γ=0,不计色散效应,则式(33)和式(34)蜕化到SSW方程开阔海域的解。
3 计算结果与分析
基于SSW方程,采用式(19)和式(20)计算浅水开阔海域亚临界航速舰船水压场,2种方法 (傅离叶积分变换法和源汇分布法)计算得到的舰船水压场纵向通过特性曲线符合良好,如图2所示。由于未计及色散性影响,故计算得到的舰船水压场负压区呈现“V”型对称分布。船首与船尾附近出现正压峰值,船中下方出现负压峰值cpmin(cpmin为水底压力变化的最小压力系数)。在横距y=0.1L增大到y=0.5L时,负压峰值和正压峰值均减小,但负压区间宽度呈逐渐增大趋势。

图2 2种方法计算结果对比Fig.2 The comparison of two kinds ofmethods
当水深傅汝德数由Fh=0.26逐渐增加到Fh=0.64时,逐渐增大,说明在船中下方产生的水压信号逐渐明显,如图3所示。但在Fh≤0.3时,舰船水压场纵向通过曲线形状基本保持不变,说明此时舰船兴波对舰船水压场的影响很小,兴波效应可以不予考虑。而当Fh>0.3时,与Fh关系密切,舰船水压场需要计及兴波影响。
当水深由0.1L逐渐增大至0.5L时,因为水底距离船体变远,因而迅速减小,说明舰船水

图3 不同水深傅汝德数下的水压通过曲线Fig.3 Longitudinal curves of pressure at different Fh
压场属于近场,舰船引起的压力扰动在深度方向衰减较快,如图4所示。
在矩形航道情况下,为满足岸壁不可穿透条件,相当于在舰船左右两侧存在一系列舰船镜像,所有镜像的贡献将导致舰船水压场的负压峰值比开阔海域的结果要大。当岸壁宽度逐渐增大时,岸壁效应逐渐减弱,逐渐减小,如图5所示。当w>5L时,舰船水压场通过曲线与开阔海域计算结果基本一致,说明此时岸壁影响可以忽略不计。
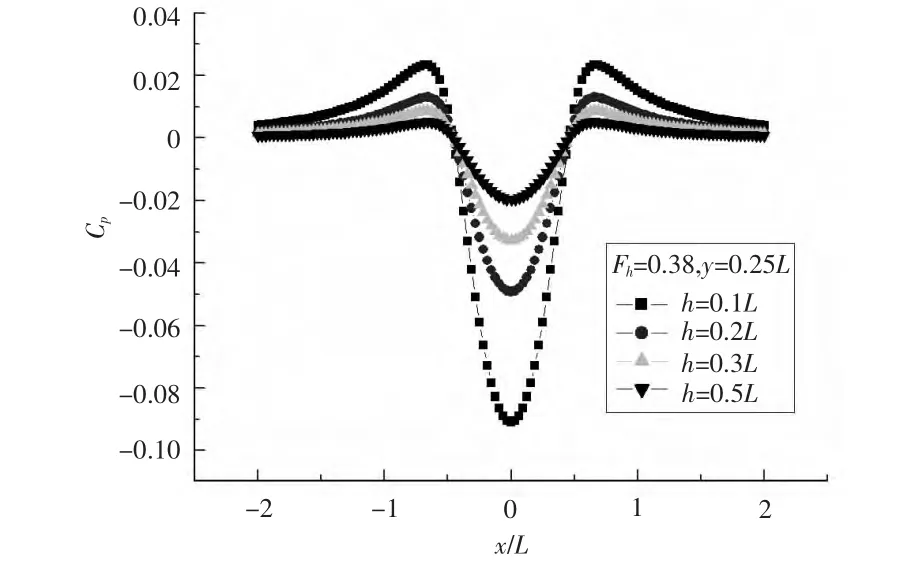
图4 不同水深下的水压通过曲线Fig.4 Longitudinal curves of pressure at different depth
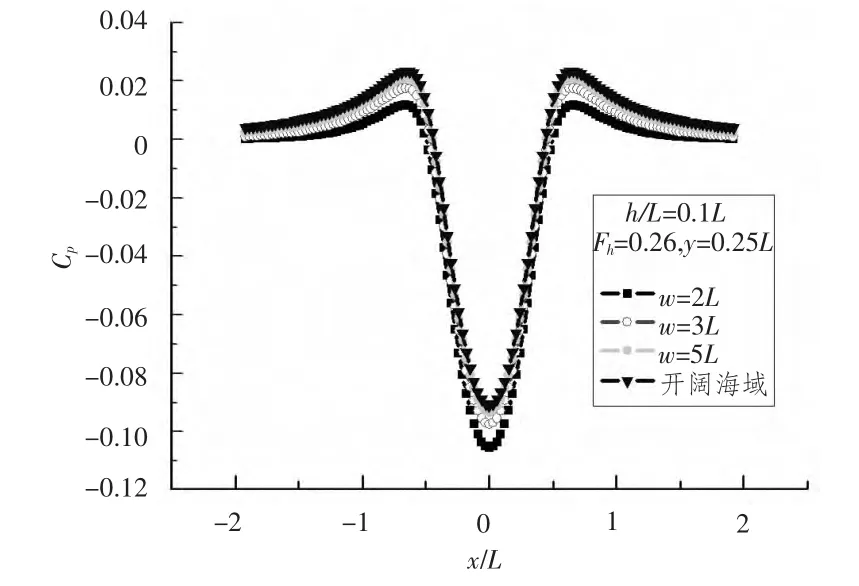
图5 不同宽度下的水压通过曲线Fig.5 Longitudinal curves of pressure at differentwidth
基于LTSW方程,考虑色散效应,采用式(33)和式(34)计算亚临界和超临界航速条件下舰船水压场的空间分布,如图6和图7所示。在h=0.1L及Fh=0.88的亚临界航速情况下,类似水面兴波现象,舰船水压场分布呈现散波与横波的特点,舰船水压场负压区不再呈现对称的“V”型分布,而具有明显的后移特征。当Fh增大时,散波夹角随之增加,负压峰值进一步后移,甚至有可能移至船尾之后。当Fh→1时,散波逐渐消失,在船首、船尾附近出现2道明显的横波。在h=0.1L及Fh=1.8的超临界航速情况下,舰船水压场的横波逐渐消失,散波逐渐加强,散波夹角随Fh增加而减小,且压力系数峰值呈现下降趋势。

图6 亚临界航速舰船水压场Fig.6 Ship hydrodynamic pressure field at subcritical speed
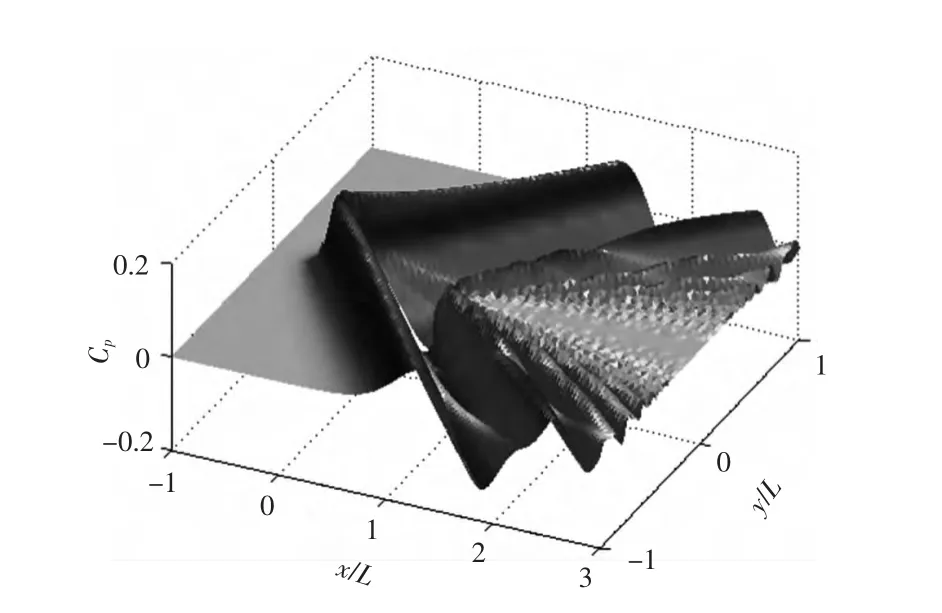
图7 超临界航速舰船水压场Fig.7 Ship hydrodynamic pressure field at supercritical speed
4 结语
基于势流理论和薄船假定,在开阔海域和矩形航道中建立了基于SSW和LTSW控制方程的浅水舰船水压场理论模型,采用傅离叶积分变换法获取了舰船水压场理论解,并与源汇分布法计算结果进行了比较,验证所建立模型的正确性和有效性。同时分析了舰船航速、水深、航道宽度、色散效应等因素对舰船水压场的影响。结论如下:
1)在浅水亚临界航速条件下,基于SSW控制方程,计算得到的舰船水压场负压区呈现对称的“V”型分布,船首与船尾附近出现正压峰值,船中下方出现负压峰值。负压峰值随Fh增大而增大,但当Fh≤0.3时,舰船水压场与Fh基本无关,说明此时舰船兴波对水压场的影响可以忽略。水深对舰船水压场影响明显,舰船水压场随水深增加衰减较快,说明舰船水压场属近场。岸壁的存在相当于舰船系列镜像的作用,并导致舰船水压场的负压峰值增加,但当w>5L时,岸壁影响可以忽略不计。
2)在浅水开阔海域条件下,基于LTSW方程,考虑色散效应,计算得到的亚临界和超临界航速舰船水压场空间分布具有表面兴波的特征。亚临界航速舰船水压场负压区不再是对称的“V”型分布,而是呈现散波与横波的特点,并具有明显的后移特征。在超临界航速情况下,舰船水压场的横波逐渐消失,散波逐渐加强,散波夹角随Fh增加而减小,且压力系数峰值呈现下降趋势。考虑色散性效应时,由于航道中舰船水压场理论模型中的被积函数存在无限多个不等距奇点,计算较为复杂,留待以后进一步分析和解决。
[1]TUCK E O.Shallow water flows past slender bodies[J].Fluid Mech,1966(26):81 -95.
[2]MULLER E.Analysis of the potential flow field and of ship resistance in water of finite depth[J].I.S.P.,1985(32):266-277.
[3]SAHIN I,HYMAN M C.Simulation of three-dimensional finite-depth wave phenomenon formoving pressure distributions[J].Ocean Engineering,2001,28(12):1621 -1630.
[4]NGUYEN T C.Integral representation of linear free-surface potential flows for bottom pressure calculation[C].Oceans 2009,MTS/IEEE Biloxi-Marine Technology for Our Future:Global and Local Challenges,2009.
[5]JIANG Tao.Ship waves in shallow Water[R].Germany:Fortschritt-Berichte VDI,2001.
[6]GOURLAY T P.Flow beneath a ship at small underkeel clearance[J].Journal of Ship Research,2006,50(3):250-258.
[7]GOURLAY T P.Slender-body methods for predicting ship squat[J].Ocean Engineering,2008,35(2):191 - 200.
[8]黎昆,张志宏,顾建农,等.利用面元法计算舰船在水底引起的压力分布[J].海军工程大学学报,2011,23(1):43 -46.
LIKun,ZHANG Zhi-hong,GU Jian-nong,et al.Calculating pressure distribution on water bottom caused by a moving ship with panelmothod[J].Journal of Naval University of Engineering,2011,23(1):43 -46.
[9]缪涛,张志宏,顾建农,等.面元法求解有限水深船舶兴波及水底压力变化[J].计算力学学报,2012,29(3):464-469.
MIAO Tao,ZHANG Zhi-hong,GU Jian-nong,et al.The calculation of ship wave and bottom pressure variation in finite depth by panel method[J].Chinese Journal of Computational Mechanics,2012,29(3):464-469.
The theoretical solution and calculation of the hydrodynam ic pressure field of ship in the shallow channel
SUN Bang-bi,ZHANG Zhi-hong,LIU Ju-bin,DENG Hui
(College of Science,Navel University of Engineering,Wuhan 430033,China)
Based on the shallow water wave potential flow theory,at low subcritical speed and linear transcritical speed shallow water wave governing equations were established.According to slender ship assumption,The theoretical solution of hydrodynamic pressure field caused by ship moving at shallow water channelwas obtained by using Fourier integral transform method.The influences ofmoving speed of ship,the wide of channel,depth of water and dispersion effect on the ship hydrodynamic pressure field were analyzed by using numerical simulation,and the resultswere compared with the ones of sources distribution method.Themathematicalmodel and the calculation method were validated.
shallow water;channel;ship;hydrodynamic pressure field;theoretical solution
U661.1
A
1672-7649(2014)04-0011-06
10.3404/j.issn.1672-7649.2014.04.002
2013-06-13;
2013-07-12
国防预研基金资助项目(513030203),海军工程大学自然科学基金资助项目(HGDQNEQJJ12002)
孙帮碧(1990-),男,硕士研究生,研究方向为舰船水压场。

