脉动球源辐射噪声的快速多极边界元方法预报

莫登沅，杨琼方，魏应三

(海军工程大学动力工程学院，湖北武汉430033)

舰艇水下辐射噪声主要包括结构辐射噪声和直接辐射噪声两类，其中，舰艇内部机械设备振动激励船体辐射噪声、推进器脉动推力和力矩通过轴系诱导船体振动所激起的辐射噪声以及舰艇外部湍流激励诱导船体振动所激起的辐射噪声，均从属于结构噪声范畴［1］.结构噪声数值预报通常采用的方法有:声学有限元方法(FEM)、声学有限元结合声学无限元方法(IEM)、声学边界元方法(BEM)和统计能量法(SEA)［2］.针对大尺度船体结构而言，FEM 显得无能为力，即使是融入IEM方法，FEM目前也仅限于分析中低频段，无法满足工程应用需求.此外，虽然借助能量作为描述动力学子系统状态的基本参数，可以采用SEA方法来求解结构模态密集的高频段噪声，但是因耦合损耗因子和模态密度通常难以确定，加上大尺度结构噪声源中子系统之间的相互耦合影响加大，使得SEA 也难以真正在方案设计阶段的实尺度船体结构噪声预报中得到应用.

尽管BEM实现了对物理问题的降维求解，但传统BEM求解时计算量为网格节点的二次方量级，对于实尺度舰艇结构来说仍然是无法承受的.目前国际上采用传统BEM能够求解的计算量为10 ～20 万自由度［3－4］，该上限很难再突破.

为了解决这一工程应用限制，快速边界元算法(Fast-BEM)开始在国际声学领域展露头脚，使得理论求解自由度达到了百万甚至千万量级，理论上为实尺度船体结构噪声的工程快速预报扫清了障碍.Fast-BEM的原型最初由Rokhlin于1985年提出［5］，主要用于求解二维 Laplace积分方程.该算法真正用于大型声学问题计算与校验开始于2002年［6］，在随后的十年期间，多种快速求解技术得到了深入的发展和应用，包括快速多极边界元方法(FMM)、自适应正交近似法(ACA)、极端优化传统边界元方法(CBEM)、高频边界元方法(HFBEM)等.FMM因专业噪声分析商用软件LMS Virtual Lab和开源程序FastBEM Acoustics的嵌入使用而得到了快速普及和推广应用.

为了准确评估FMM算法在辐射噪声预报时相对于传统边界元方法的计算优势、计算效率、计算精度以及当前仍然存在的问题，文中以最为常见的脉动球源辐射噪声为对象，分别讨论了FMM算法在无限空间内脉动球源噪声、半无限空间内脉动球源噪声以及有源激励下脉动球源辐射噪声预报中的应用，为FMM算法扩展用于大尺度结构噪声预报奠定基础.

1 快速多极边界元算法的理论模型

在各项同性、不可压、无粘、无局部声源的均相流体介质中，简谐声源的声波动方程可描述为亥姆赫兹方程［7］:

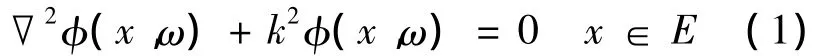
式中:φ(x，ω)为频域内声压幅值，x为声源向量，ω为圆频率，c为声速，k=ω/c为波数，E为外部声场.时域内声压在频域内表示为p(x，t)=φ(x，ω)e－iωt.在满足 Sommerfeld 声辐射边界条件下，式(1)可转换为传统的边界元积分方程(CBIE):

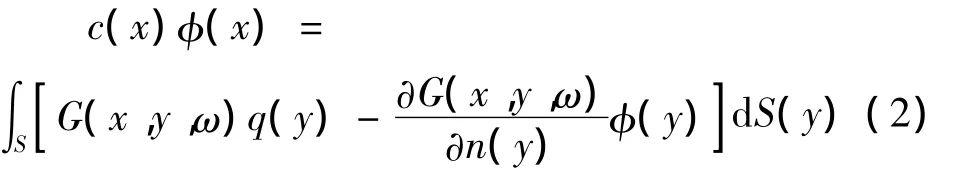
式中:当辐射体表面S为光滑壁面时，常系数c(x)=1/2，y为场点向量，q为声压外法向梯度，q=∂φ/∂n=iωρvn，n为壁面法向，ρ为流体介质密度，vn为质点法向速度，格林内核函数表示为:

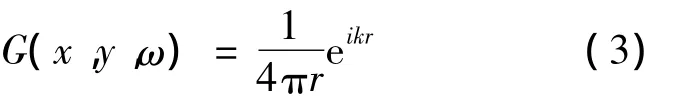
式中r为声源与场点之间距离.由式(2)可以求解得出壁面S上的声压和声压梯度，但对于外部声辐射问题来说，在内声场共振频率(奇异频率)处解并不唯一.并且当声源与场点间距离无限小时，格林函数积分项会出现奇异.为了解决这一问题，将式(2)对声源法向进行求导，得到超奇异边界积分方程(HBIE):

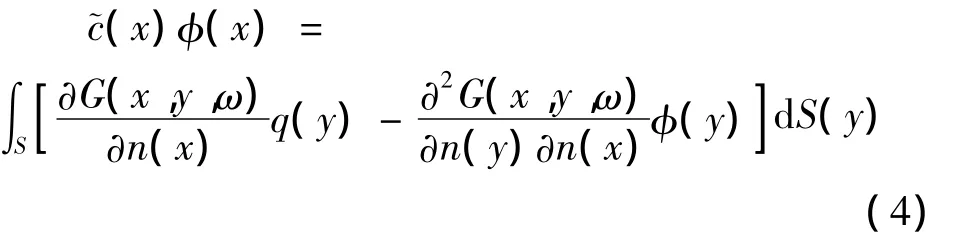
其中，光滑壁面仍取常系数~c(x)=1/2.式(4)与式(2)均描述了辐射体表面上的声压与质点速度分布情况，只是数学形式不同，同样也存在解的非唯一性问题.但是，式(4)与式(2)仅存在一个唯一的公共解，该公共解即为所需要的式(1)的唯一物理解.为了求得该公共解，将式(4)与式(2)构成耦合积分方程:

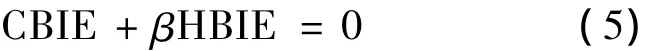
式中β为耦合系数.该耦合积分方程即为著名的Burton-Miller边界元积分方程［8］，β 推荐取i/k.

为了实现该耦合积分方程中各积分项的快速求解，首先需要将格林函数进行多极展开，这也是实现快速多极边界元求解的基础.“多极”即指的是进行极数展开的阶数.FMM计算时对式(5)离散后的系数矩阵所需要的计算量仅为声网格节点的一次方量级，远低于传统边界元求解，其核心思想是［9］:在求解系数矩阵时采用迭代计算以加速每步迭代中的系数矩阵与特征变量的乘积解，而不需要完整地给出系数矩阵的最终解.快速多极扩展求解仅用于远离声源的场点求解，而对于近壁面的声网格单元来说，仍需要采用传统的直接积分求解.在采用FMM算法后，对于内存为2G的普通PC机来说，计算量也可以达到10万网格单元.

2 脉动球源辐射噪声的快速多极边界元法预报

所分析脉动球源半径R=1 m，球源在径向方向的振动速度为1 m/s.采用快速多极边界元专业软件Fast-BEM进行求解.该软件是美国Ohio洲先进CAE研究所开发的一款快速边界元计算软件，与当前两款主流的振动噪声预报软件ANSYS和Nastran均具有数据接口.该软件由Liu Y J博士领衔研发［10－13］，2014 年 1 月发布了最新版本 4.0，并且向全世界公开了用于学习使用的免费学生版.应用FMM算法时的输入文件如图1.分析频率为545.9 Hz，对应特征波数为ka=20，a为球源直径.动画演示项参数1表示输出动画文件，其后参数one表示将最后一个频率下的求解结果输出为Tecplot图像文件.应用快速多极边界元算法求解时的展开极数设置为10.

图1 脉动球源快速多极边界元算法求解输入文件Fig.1 Input file of fluctuating sphere source into Fast-BEM

计算得到水平面内空间场点的声压级云图如图2，图中同时给出了解析解.参考声压为20 μPa.可以看出，FMM计算结果与解析解几乎无差别，很好地证明了该算法的求解精度.为了进一步与船舶结构噪声预报对应，将上述脉动球源置于一刚性或弹性半无限壁面外，以模拟船体底板对螺旋桨声反射和散射的工作条件.同时，为了与螺旋桨噪声贡献量最为突出的低频线谱对应，将求解频率降低到特征波数为ka=2，可用于描述螺旋桨3倍叶频线谱，对应五叶桨的转速为218.36 r/min.脉动球源与壁面之间的距离为1 m.此时，FMM求解输入文件相对于案例一来说，第二行设置条件改为Half，3，1.d0，意思是求解壁面外的半无限空间声场、壁面以z轴为法向平面、壁面为刚性、吸声系数为0.计算得到壁面上声压和声速分布云图如图3.可以看出，因声反射影响，壁面上声压与声速近似反相.

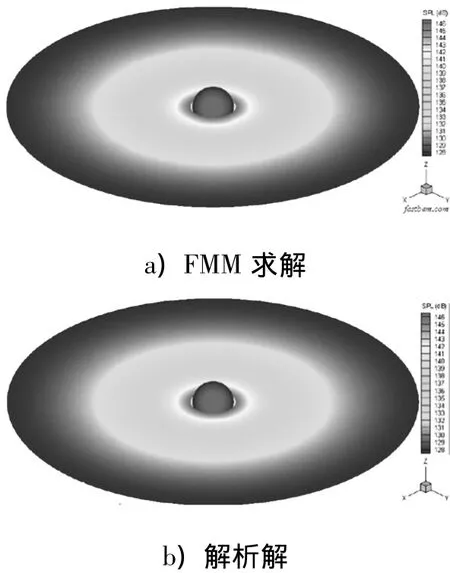
图2 单位振速脉动球源特征波数ka=20时声压级云图Fig.2 Contour of sound pressure of fluctuating sphere source with unit velocity at ka=20

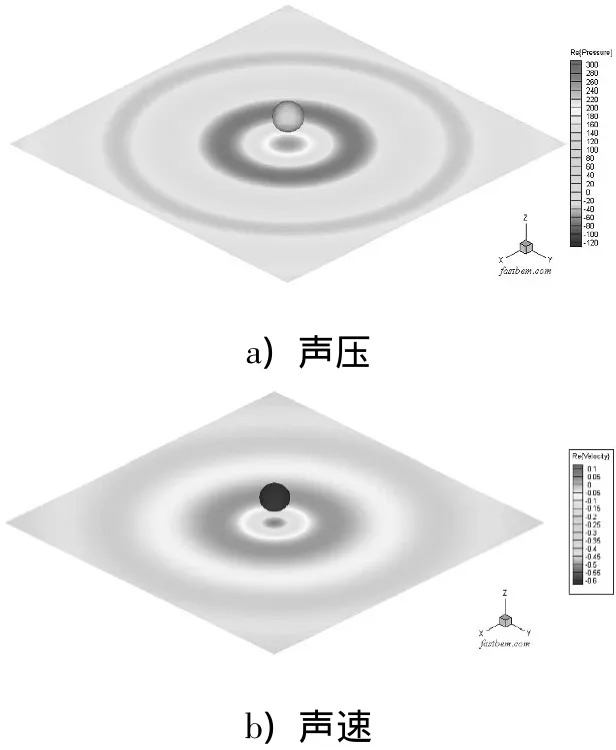
图3 单位振速脉动球源特征波数ka=20时刚性壁面上声压和声速分布云图Fig.3 Contour of sound pressure and sound velocity on rigid plane of fluctuating sphere source with unit velocity at ka=20

在上述计算分析的基础上，因桨叶壁面噪声源项和船体内部机械设备激励源项分布都是非均匀的，为了更加接近于工程实际，在脉动球源内部加载一单极源项，单极源位于x轴上半径/2处，脉动球源振动速度边界条件由单极源激励提供.仍然考虑特征波数ka=20，且将球源声网格单元数增加到10800，约为案例一的10倍.计算得到球源壁面非均匀声压分布如图4，平面空间场点的声压分布如图5.可以看出，因点源在x轴方向的非对称布置，球源壁面呈现出了一定的偶极源分布特征，而对于平面空间声场点来说，类似于平面波的入射和散射效应，仅有声源所在位置呈现出了声亮点.这与声源定位的思想一致.

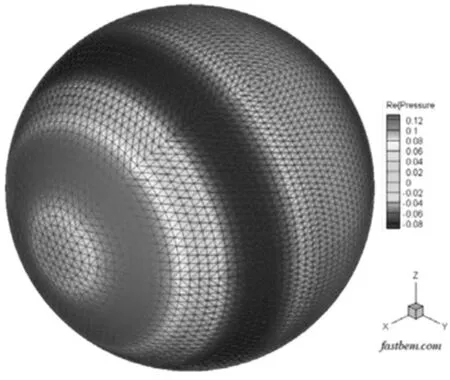
图4 单极源激励下球源壁面特征波数ka=20时声压云图Fig.4 Contour of sound pressure on sphere surface with monopole excitation at ka=20

图5 单极源激励球源特征波数ka=20时平面声压云图Fig.5 Contour of sound pressure on plane with monople excitation at ka=20

上述算例表明，Fast-BEM程序及其包含的快速多极边界元算法能够应用于以脉动球源和多极子声源为基本声源的辐射噪声预报.需要注意的是，目前FMM算法仅适用于三角形网格，如图4中球源壁面声网格所示，这与结构壁面流体载荷高精度计算流体动力学分析(CFD)时优先采用的全六面体结构化网格是不一致的.也就是说，将壁面四边形网格上的流体载荷变量加载到结构三角形声边界元网格时存在映射传递，变量映射的完整性和插值传递格式会直接影响最终声边界元的计算结果.因此，在计算资源允许的条件下，声边界元网格密度应尽量靠近CFD网格.推荐的一种数据映射插值传递格式如图6，此时搜索距离为单位波长内6个有效声网格的距离.

图6 流体网格到声边界元网格节点变量映射传递格式Fig.6 Acoustic mesh mapped from CFD mesh nodes

3 快速多极边界元算法精度和计算效率分析

在上节中分析FMM应用于多极声源辐射噪声预报的基础上，为了更清晰地说明该算法的计算精度和计算效率，再对一活塞球源进行分析，分析结论可为自主开发FMM源程序作铺垫.

活塞球源半径rs=1 m，球源表面法向速度满足以下边界条件:

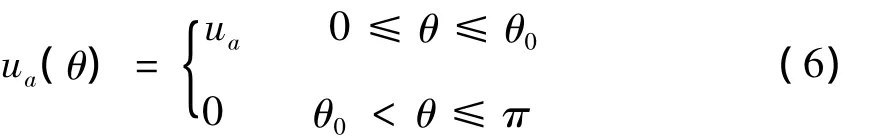
其中:ua=0.001 m/s，θ0=75°.

采用快速多极边界元对该声源进行数值计算，分析过程中共采用7组由稀到密的网格单元，自由度数分别为:768，3 072，6 912，12 288，19 200，76800，307 200，分析频率的波数为 2π，每组网格皆满足一个波长10个网格单元的要求.FMM数值计算时，多极展开项数为6，收敛误差设置为10－4.

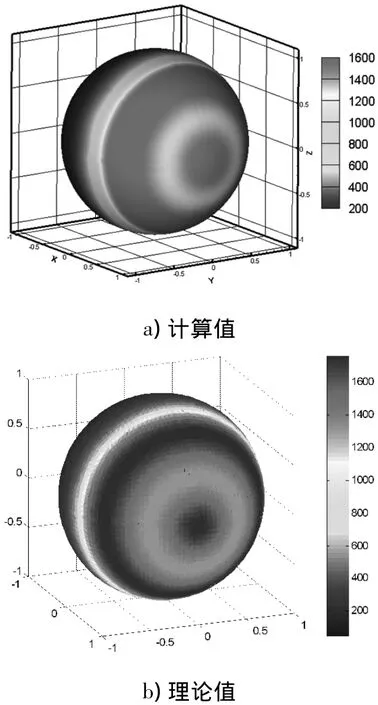
图7 快速多极边界元计算声压与理论值对比Fig.7 Comparison of calculated sound pressure on sphere surface

FMM计算得到球源表面声压与理论值对比如图7.从该声压分布云图可知，计算值与理论值量级及分布规律皆吻合较好，证明所采用FMM算法精度可靠.为了清晰展示FMM算法的计算效率，再次采用常规边界元方法计算不同网格下的活塞球源声辐射，两者所需时间比如图8.当自由度达到19200时，因常规边界元对计算内在的限制，导致计算无法进行，而采用快速多极边界元只需73s，甚至当自由度数超过30万时，在单机上计算一个频率也只需1714 s，这是常规边界元方法短期内无法解决的.FMM算法计算得到7组网格的声功率级和功率误差如表1.可以看出，当自由度达到常规边界元无法计算的量级时，声功率级误差仅为0.07dB，此时能够较好地兼容计算效率与计算精度两者的关系.

图8 常规边界元与FMM算法计算时间比较Fig.8 Comparison of cost time between BEM and FMM

表1 快速多极边界元计算误差Table 1 Numerical erros of FMM with different meshes

4 结论

快速多极边界元算法是快速边界元数值技术中的代表性技术，是解决实际工程应用中大规模声学问题数值预报的关键技术.本文以单位振速脉动球源、刚性壁面外单位振速脉动球源、单极源激励下的球源以及单位激励活塞球源声辐射为对象，对快速多极边界元算法进行了应用和分析.结果表明，FMM能够在保持声学计算精度的条件下极大提高计算效率，具有推广用于大尺度结构辐射噪声预报的巨大潜力.不足的是，FMM算法目前仅适用于三角形网格，在进行流－固－声三者耦合分析时需重点关注载荷数据的映射效果.

References)

［1］ 杨琼方.潜艇流噪声和推进器噪声的数值预报和分析［D］.武汉:海军工程大学，2011.

［2］ 魏应三.舰艇水下辐射噪声数值计算方法研究［D］.武汉:海军工程大学，2012.

［3］ 曾革委.潜艇结构辐射噪声的建模、求解及其声特性研究［D］.武汉:华中科技大学，2002.

［4］ 李善德.大规模声学问题的快速多极边界元方法研究［D］.武汉:华中科技大学，2011.

［5］ Rokhlin V.Rapid solution of integral equations of classical potential theory［J］.Journal of Computational Physics，1985，60:187 －207.

［6］ Sakuma T，Yasuda Y.Fast multipole boundary element method for large-scale steady-state sound field analysis，Part I:setup and validation［J］.Acta Acustica United with Acustica，2002(88):513 －525.

［7］ Ross D.Mechanics of underwater noise［M］.New York:Pergamon Press，1976.

［8］ Burton A J，Miller G F.The application of integral equation methods to the numerical solution of some exterior boundary-value problems［C］∥Proceedings of the Royal Society of London，Series A.London:Royal Society of London，1971，323:201 －210.

［9］ Advanced CAE research［G］.［S.l］:FastBEM Acoustics User Guide，LLC，2014.

［10］ Liu Y J，Nishimura N.The fast multipole boundary element method for potential problems:a tutorial［J］.Engineering Analysis with Boundary Elements，2006，30:371－381.

［11］ Liu Y J，Shen L.A dual BIE approach for large-scale modeling of 3D electrostatic problems with the fast multipole boundary element method［J］.International Journal for Numerical Methods in Engineering，2007，71:837－855.

［12］ Shen L，Liu Y J.An adaptive fast multipole boundary element method for three dimensional acoustic wave problems based on the Burton-Miller formulation［J］.Computational Mechanics，2007，40:461 －472.

［13］ Liu Y J.Multipole boundary element method-theory and applications in engineering［M］.Cambridge:Cambridge University Press，2009.