串列双圆柱绕流换热特性的数值研究

张东辉, 石 珊, 王 军, 陈 宁

(江苏科技大学 能源与动力工程学院， 江苏 镇江 212003)

串列双圆柱绕流换热特性的数值研究

张东辉, 石 珊, 王 军, 陈 宁

(江苏科技大学 能源与动力工程学院， 江苏 镇江 212003)

采用有限体积法,对双尺度串列圆柱的绕流换热进行二维瞬态数值模拟.主圆柱直径D固定,小圆柱直径d从0.2D变化至D.基于主圆柱直径D的ReD数为100和200.在间距比L/D=2,3,3.5,4,5,7下进行模拟.小圆柱分别放置在主圆柱的前面和后面.在经过与其他文献细致的比较验证后,研究表明:对于双尺度串列圆柱布置,流动型态转变的临界间距比在2和4之间.上游圆柱的存在使得下游圆柱的平均阻力系数有很大的降低,但其本身的平均阻力系数受到下游圆柱的影响较小;小圆柱后置较前置情况,对换热更为有利;而且,当两圆柱的间距大于4后,系统总换热量随间距的改变变化很小,且此时d/D=0.8和d/D=1两种情况下总换热量增长率很接近,这意味着在列管式换热器中,有可能采用大小直径的圆柱组合,一方面体积换热变化很小,另一方面却可达到节约管材耗量的效果.

多尺度结构;圆柱绕流;对流换热

圆柱绕流是一个经典的流体力学问题.当流体绕圆柱体流动时,由于过流断面收缩,沿程流速增加,压强减小,最终在柱体周围形成附面层的分离.圆柱的存在也会使得圆柱迎水面产生壅水现象,从而增加了圆柱的受力,使得圆柱绕流问题变得十分复杂.不仅如此,圆柱绕流换热也被广泛地应用在换热器、冷却塔、发电机等工程实践中.圆柱群的排列[1]、尺寸、间距等都会影响到流体的流动型态和换热效果.因此,了解其机理对于换热器等的强化换热有着重要的实际意义.

在多圆柱结构中最简单的结构就是串列双圆柱.关于等直径的串列双圆柱尾流的研究有很多[2-4].通过这些文献可以总结3种基本的尾流型态:1)当L/D较小时为单一钝体型态(single bluff-body behavior);2)当L/D处于中间值时为剪切层再附着型态(shear layer reattachment behavior);3)当L/D较大时,每个圆柱尾流都有卡门涡的脱落,也叫做共同脱落型态(co-shedding regime).文献[5]利用数值方法研究了流体流过2个和3个圆柱的流动规律.其中圆柱分别为串列和并列布置并改变圆柱与圆柱之间的间距.模拟计算了平均升阻力系数以及Strouhal数.研究表明对于多个圆柱的绕流,雷诺数非常重要,并且所有圆柱的Strouhal数相同.

对于等直径圆柱与流体之间换热的研究,文献[6]研究了流体绕流串列双圆柱的尾流流动结构、动量和热量传递.两个圆柱中的上游圆柱是发热的.实验的测量结果是在Re=7000,L/D=1.3,2.5,4,6,10,20,30下得到的.结果显示2个圆柱的雷诺应力和热流量的分布在一定的x/D下是不同的.文献最后还总结了不同流动型态下的动量和热量传递特点.文献[7]模拟研究了流体与串列双圆柱的层流换热规律.研究表明,对于高雷诺数的流动,下游圆柱的局部Nu数的分布会出现两个最大值,上游圆柱的平均Nu数在L/D>4时与单圆柱的结果相近.文献[8]也利用数值模拟的方法同样的研究了流体横掠2个和3个的串列恒温圆柱,并且提出了计算相应柱群结构的平均Nu数的关联式.

对于流体绕流2个直径不同的串列圆柱的情况,文献[9]数值研究了Re数为200时串列圆柱尾迹的流动规律,直径比d/D为一固定值2/3.文中根据L/D不同将流动规律归为3类:当L/D<1.8,圆柱对表现出单一钝体的特点;当L/D∈[1.8, 3.8]时,流动出现双稳态现象,即上下游圆柱旋涡脱落的频率相同;当L/D>3.8时,总是会出现共同脱落的现象.

众所周知,圆柱后面的尾流结构会影响其换热特点.然而,流体流过多圆柱的情况和流过单圆柱的情况是不相同的.文献[10]的研究表明与常规结构相比,不同直径圆柱的布置使得微粒沉降率显著减少.那么在换热器中多尺度对换热量和压降等会带来怎样的影响,则需要作进一步研究.

1 控制方程和边界条件

1.1 控制方程

二维非稳态、层流、不可压缩、常物性流体在笛卡尔坐标系统中的控制方程如下:

连续方程

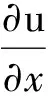
(1)

动量方程

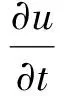
(2)

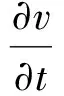
(3)

能量方程

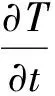
(4)

式中：u和v是速度在x和y方向上的分量；p为压强；ν是运动粘度；ρ为流体密度；T是流体温度；α为热扩散率定义为λ/ρc,λ是流体热导率,c为流体热容量.

1.2 边界条件

计算区域以及圆柱的结构如图1.边界条件设置如下:进口为均匀来流;出口流体假定充分发展,定义为自由流出口条件;上下边界距离圆柱距离较远因此定义为对称边界;圆柱表面为恒温无滑移壁面.

图1 双圆柱情况下的计算区域Fig.1 Computational domain used in the twocylinder validation case

1.3 无量纲参数

单圆柱升阻力系数的计算公式为:

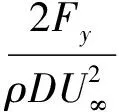
(5)

式中：D为圆柱的特征尺寸,对于小圆柱来说其特征尺寸为d；Fx和Fy分别为力在x方向和y方向上的分量.

主圆柱平均阻力系数的减少率,即系统在增加了小圆柱后,主圆柱的平均阻力系数减少百分比,以单圆柱平均阻力系数为衡量基准：

(6)

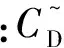
系统总换热量增长率，即系统在增加了小圆柱后系统总换热量的增加百分比以单圆柱换热量为衡量基准:

Q～=(Qsystem-Q0)/Q0

(7)

式中：Qsystem为两圆柱总换热量即(Q1+Q2);Q0为单圆柱换热量.

2 模拟验证

2.1 恒温单圆柱绕流情况

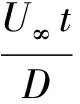
表1 单圆柱情况下计算结果Table 1 Results for single cylinder

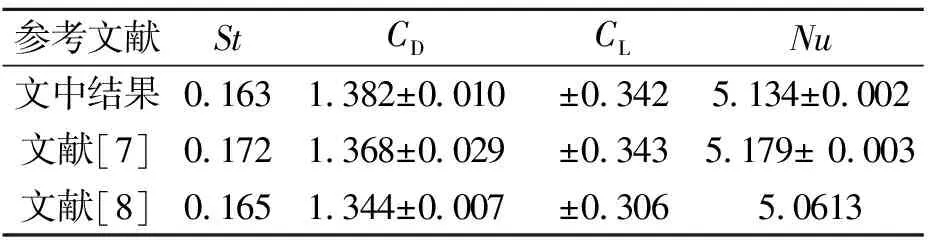
表2 ReD=100时单圆柱计算结果与文献对比Table 2 Comparison of key parameters for a singlecylinder at ReD=100

2.2 恒温等直径串列双圆柱绕流情况

为了对结果进行进一步的验证,同时比较了等直径双圆柱的情况.计算区域为长(38D+L),宽24D的矩形区域,如图1.对计算区域进行了划分使区域内的网格为结构四边形网格如图2.表3列出了部分文中计算结果与相应文献计算结果的比较.其中所选取的文献[7-8]都采用了数值模拟方法进行研究,并在模拟过程中采用了重叠网格的方法.但文献[7-8]都只讨论了等直径双圆柱的流动情况,文中通过对已有数据进行比较来验证模拟结果的正确性,进一步研究双尺度圆柱的流动和换热情况.

图2 整体和局部的网格Fig.2 General and close-up views of the mesh

表3 等直径串列双圆柱计算结果与文献对比Table 3 Comparison of key parameters for tandem cylinders of equal diameter

注：a代表参考文献[7]中的值；b代表参考文献[8]中的值.

3 结果和讨论

3.1 串列圆柱的流动型态演化

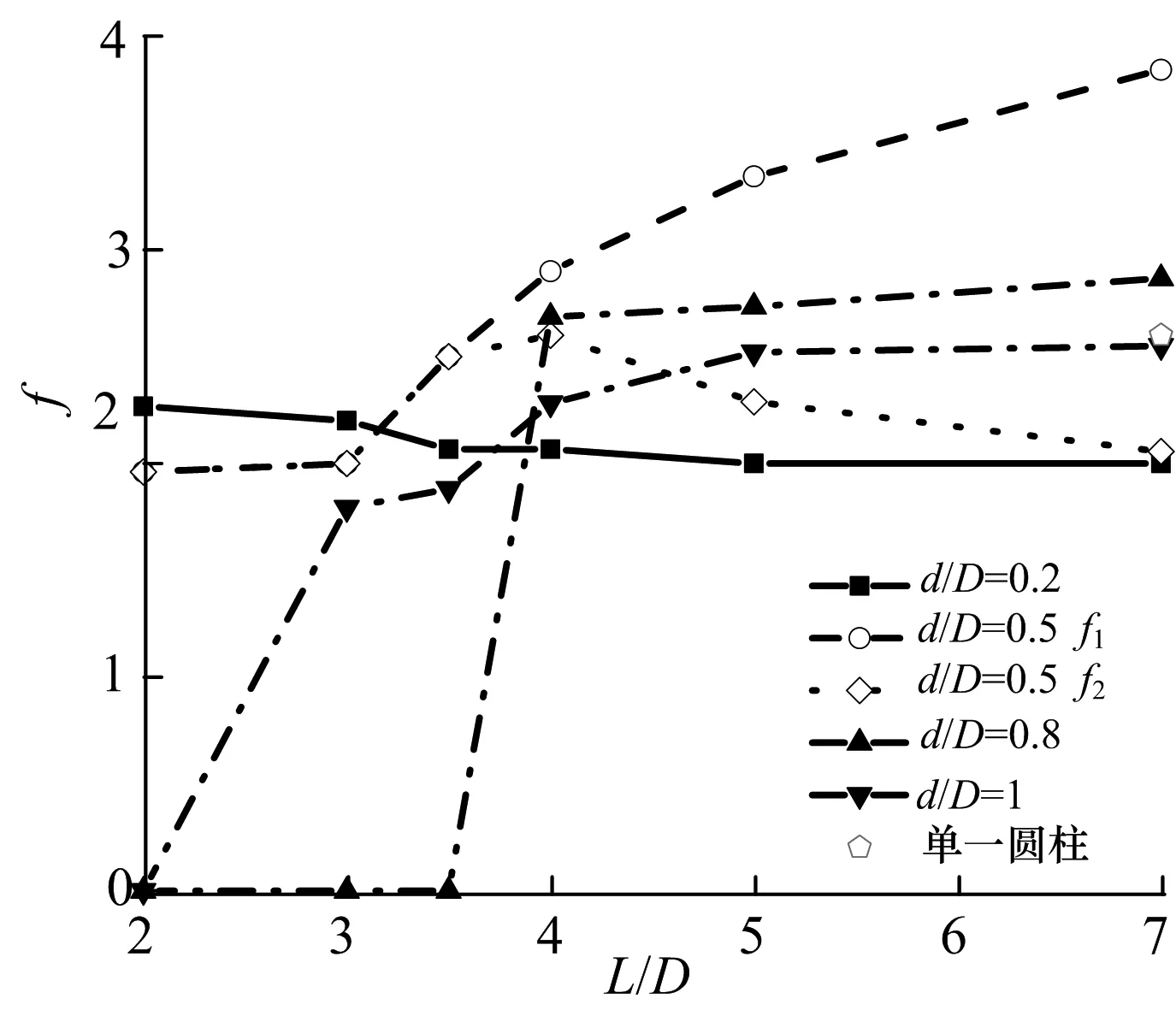
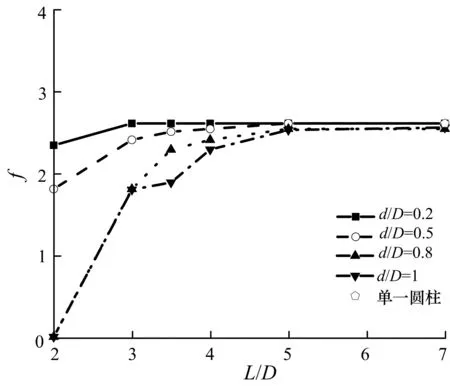
为了研究流动型态的变化,图3和图4分别给出了小圆柱前置和后置情况下的瞬时涡量,同时图5列出了对应的涡脱落频率.

图3 小圆柱前置时瞬态涡量图(ReD=100)Fig.3 Instantaneous vorticity contours when smallercylinder is upstream at ReD=100

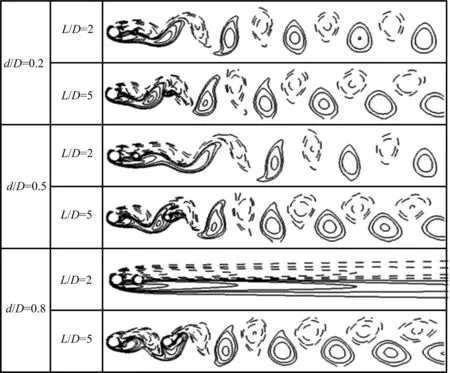
图4 小圆柱后置时瞬态涡量图(ReD=100)Fig.4 Instantaneous vorticity contours when smallercylinder is downstream at ReD=100

a)前置

b)后置

图3是小圆柱前置情况下的流场涡量图.从图中可看出,当直径比d/D=0.2时,对于所有间距比,上游圆柱尾迹都会产生一对对称的稳定的旋涡,但是并没有涡脱落的发生,这是由于基于小圆柱直径的Red数太小, 仅为20;另一方面,当前置圆柱直径过小时,其形成的剪切层很弱而不足以附着在下游圆柱表面,因此下游圆柱后面总是有旋涡的脱落,此时,所有间距下流动型态类似.尽管如此,小圆柱的存在减小了下游圆柱迎流流体的速度,因此下游圆柱涡脱落的频率相比单圆柱要小.d/D=0.5时,小间距下,上游圆柱的剪切层会附着于在下游圆柱迎流面并逐渐从上游圆柱表面脱落,最后消失在尾迹中;随着间距的增大,上游圆柱脱落的涡随着流体的运动撞击在下游圆柱表面,并从其表面脱落,与此同时,下游圆柱产生的涡也会脱落.由于两圆柱的直径不同,由图5显示,下游圆柱的尾迹中会出现两个涡脱落的频率.其中较大的频率(f1)来自上游圆柱,较小的频率(f2)来自下游圆柱.与d/D=0.5不同的是,当d/D=0.8和d/D=1时,在小间距下,上游圆柱产生的剪切层没有足够的空间发展脱落,此时两圆柱之间的流体运动速度非常低,因此对于上下游圆柱来说都不会有涡的脱落.这种情况一直维持到间距比分别为3.5(d/D=0.8)和3(d/D=1).且由于上游圆柱产生的涡量值较大,因此尾迹中只出现一个涡脱落频率.综上可得,前置情况下流型转变的临界间距比在3.5附近.

图4是小圆柱后置情况下的瞬态涡量图.当两个圆柱离得较近时,上游圆柱的剪切层会被拉长.这意味着在串列构形下,下游圆柱的存在使得上游圆柱的尾流更加稳定.比如在d/D=0.8,L/D=2的情况下,甚至没有涡脱落现象的发生,而随着下游圆柱直径的减小和两圆柱间距的增大,圆柱尾流开始出现涡街并逐渐变得更复杂,因此涡脱落的频率也会逐渐增大.一般来说,上游圆柱产生的涡脱落后会再次从下游圆柱表面脱落,此时的所有情况下,在下游圆柱尾迹也只会出现唯一一个涡脱落频率,且这个频率来自于上游圆柱.

3.2 主圆柱平均阻力系数的减少率

图6和图7为不同布置下主圆柱平均阻力系数降低的百分比.在图6中,小圆柱前置的情况下,主圆柱的平均阻力系数有明显降低,比如在ReD=200,d/D=0.2时,其降低率最小可达22%,且随着直径比d/D的增加其降低率也有所增加.这是由于小圆柱的存在一方面改变了主圆柱迎流流体的大小和方向,使得主圆柱不再是严格受到流体的横向冲刷;另一方面,小圆柱产生的涡附着或是撞击在主圆柱迎流面上,改变了主圆柱表面的压力分布.此外,雷诺数较大时,主圆柱平均阻力系数的降低率更大.这意味着此情况下双圆柱的相互作用会造成主圆柱阻力系数的明显下降.

小圆柱后置时,如前所述,小间距下上游圆柱的剪切层会被拉长,其尾迹流态更加稳定,涡脱落频率较小,因此主圆柱平均阻力系数的降低率仅在小间距下较为明显.这表明:下游圆柱的阻力受到上游圆柱的直径、距离等影响较大,而下游圆柱对上游圆柱阻力的影响并不明显.另外,在临界间距比时,阻力系数的减少率会急剧降低,即上游圆柱旋涡的脱落不仅增加了其自身的阻力,其对下游圆柱的撞击也增加了下游圆柱的平均阻力系数.

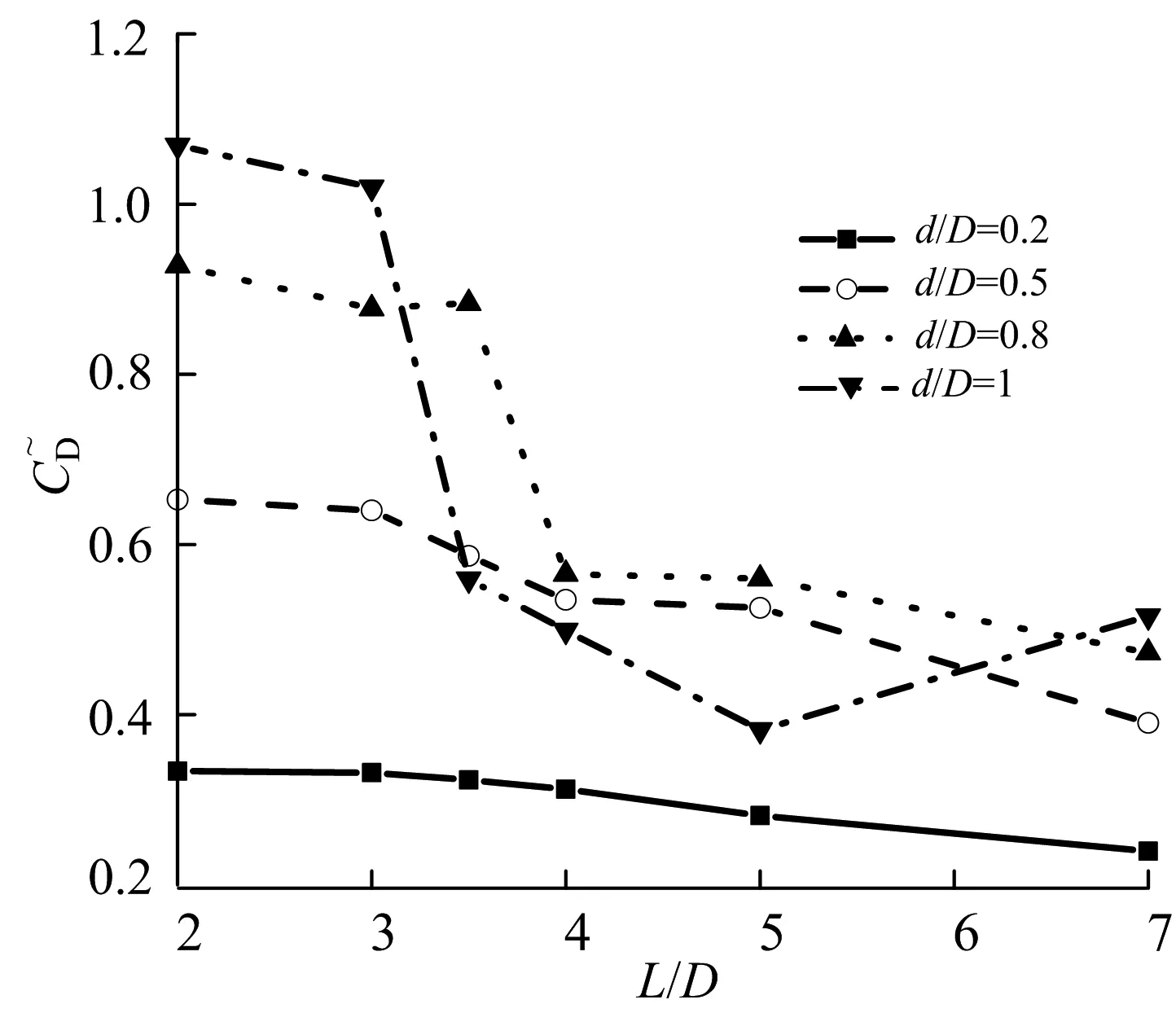
a)ReD=100

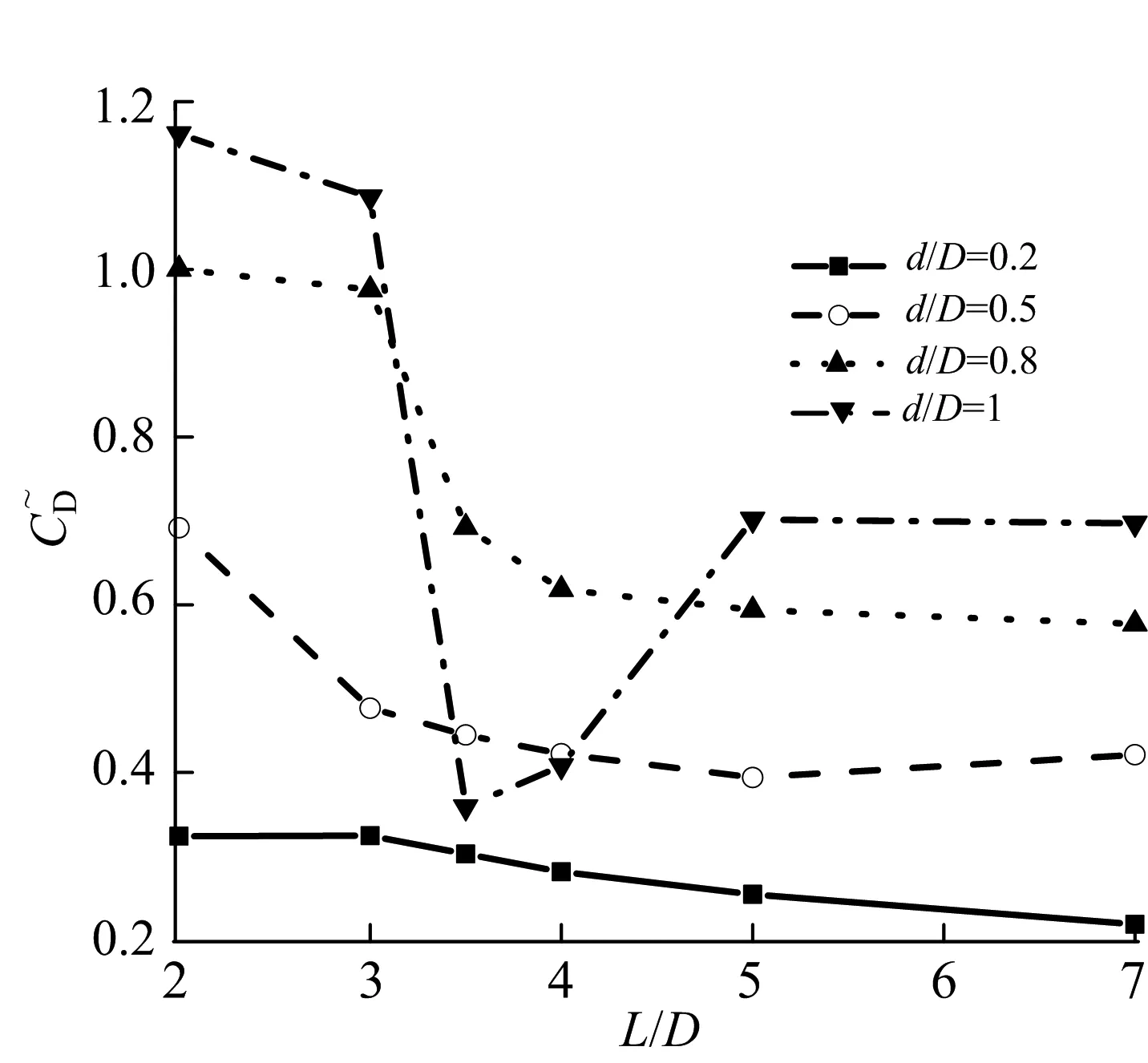
b)ReD=200

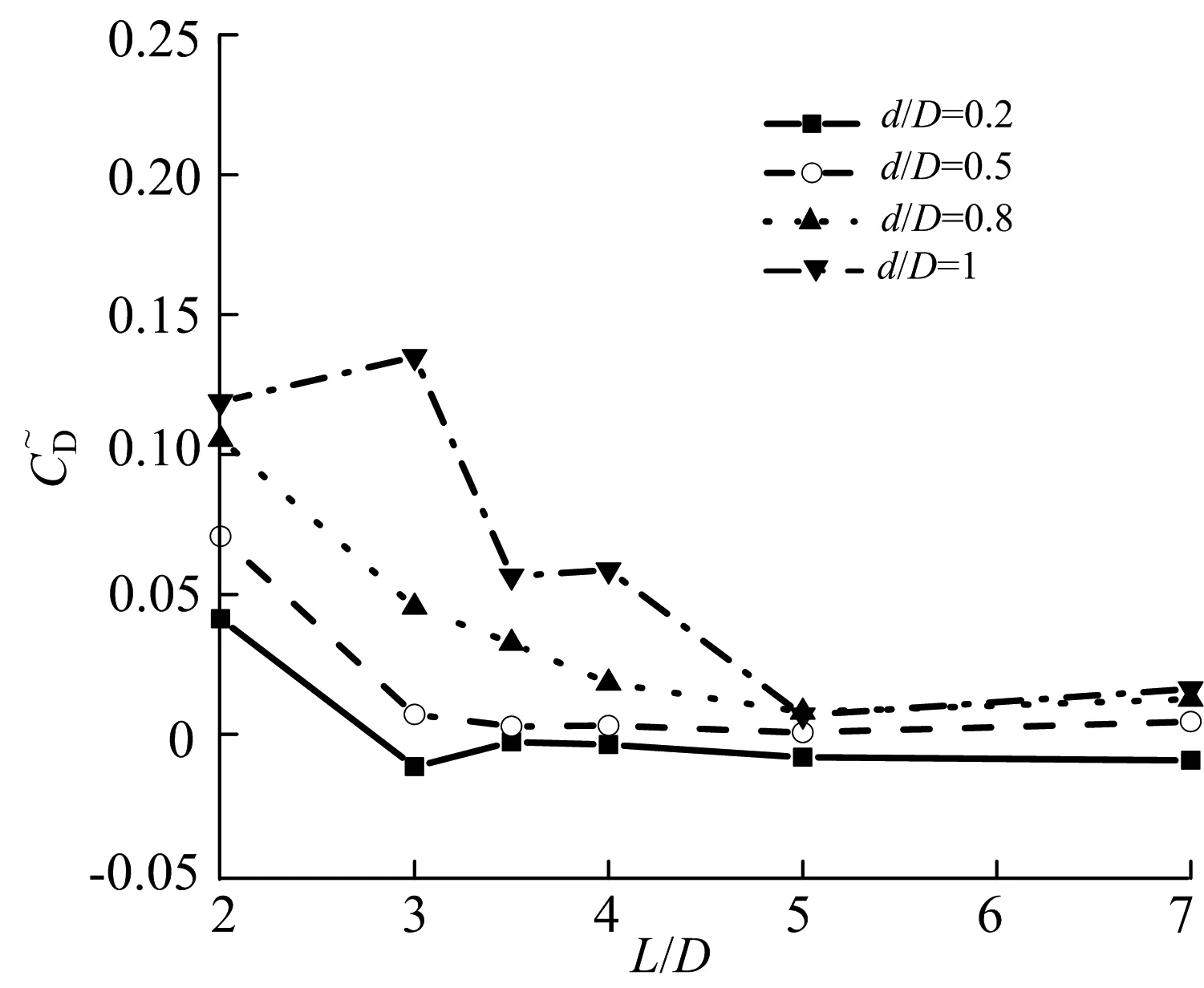
a)ReD=100

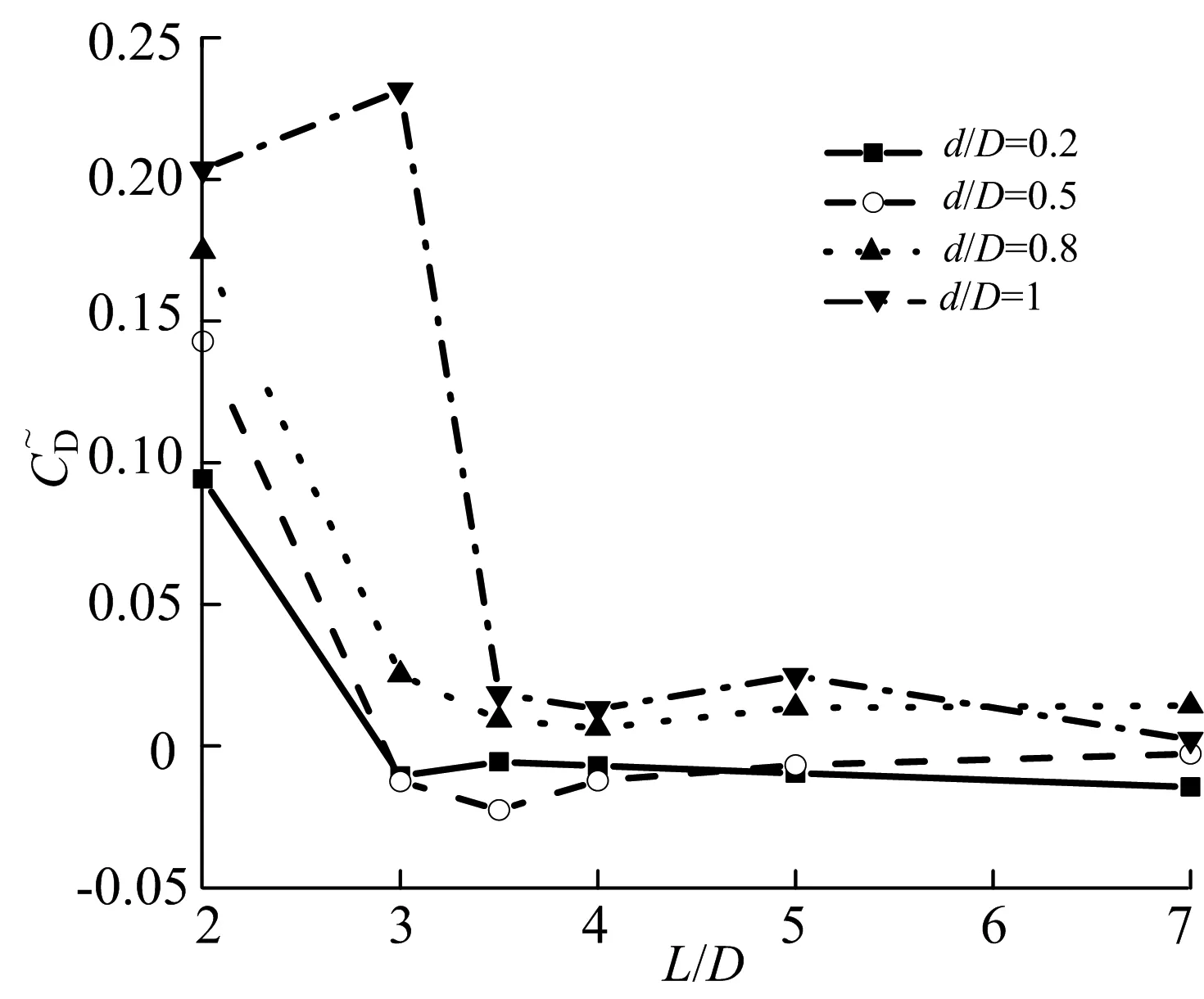
b)ReD=200

3.3 总换热量的增长率

图8和图9分别为小圆柱位于主圆柱前后时的系统总换热量增长率情况.如图中所示,在所有情况下,总换热量的增长率都不会达到100%,这意味着: 在本研究所考察的Re范围内,与两圆柱独立换热相比较,两圆柱对流场的相互作用一定会引起总换热量的损失;但与单个圆柱情况相比,总换热量都有所提高.小圆柱后置较前置情况,对系统换热更为有利.经分析发现:合适的小圆柱后置位置,一方面延迟了大圆柱的剪切层的分离,使流过大圆柱的流体可以充分地与其换热;另一方面,从大圆柱脱落的涡会再次从小圆柱表面脱落,进一步增强了小圆柱的换热.对于ReD=100,d/D=0.2的情况,小圆柱后置时,总换热量的最大增长率可达42.87%,而当其位于主圆柱之前最大仅为30.49%.

a)ReD=100

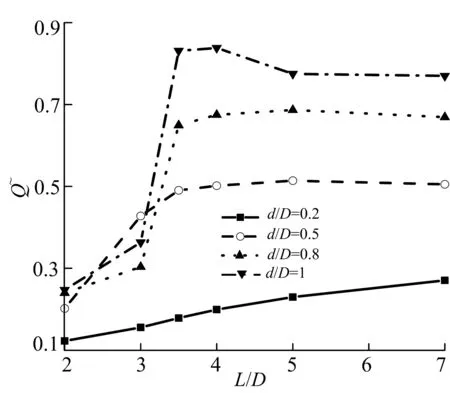
b)ReD=200

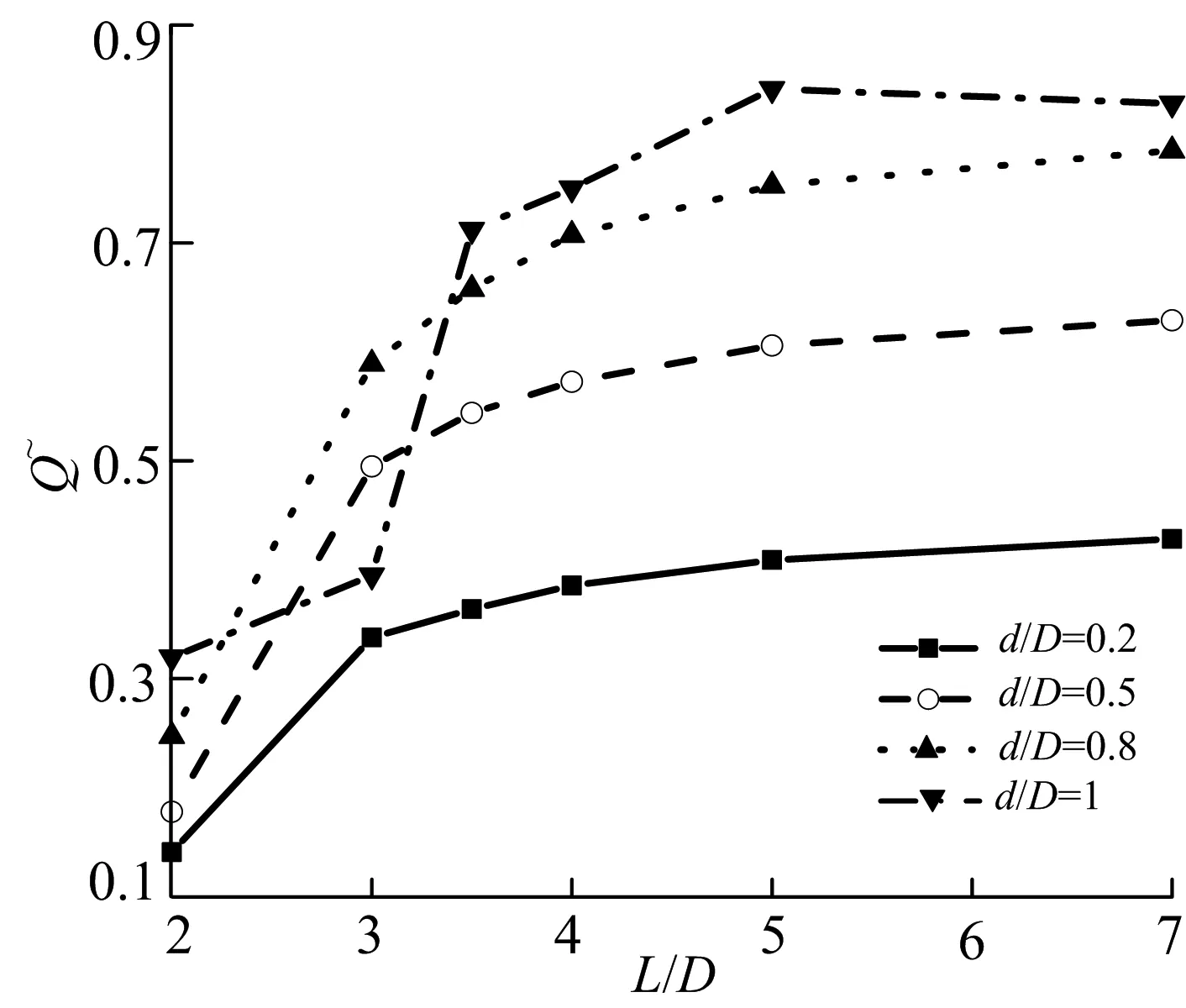
a)ReD=100

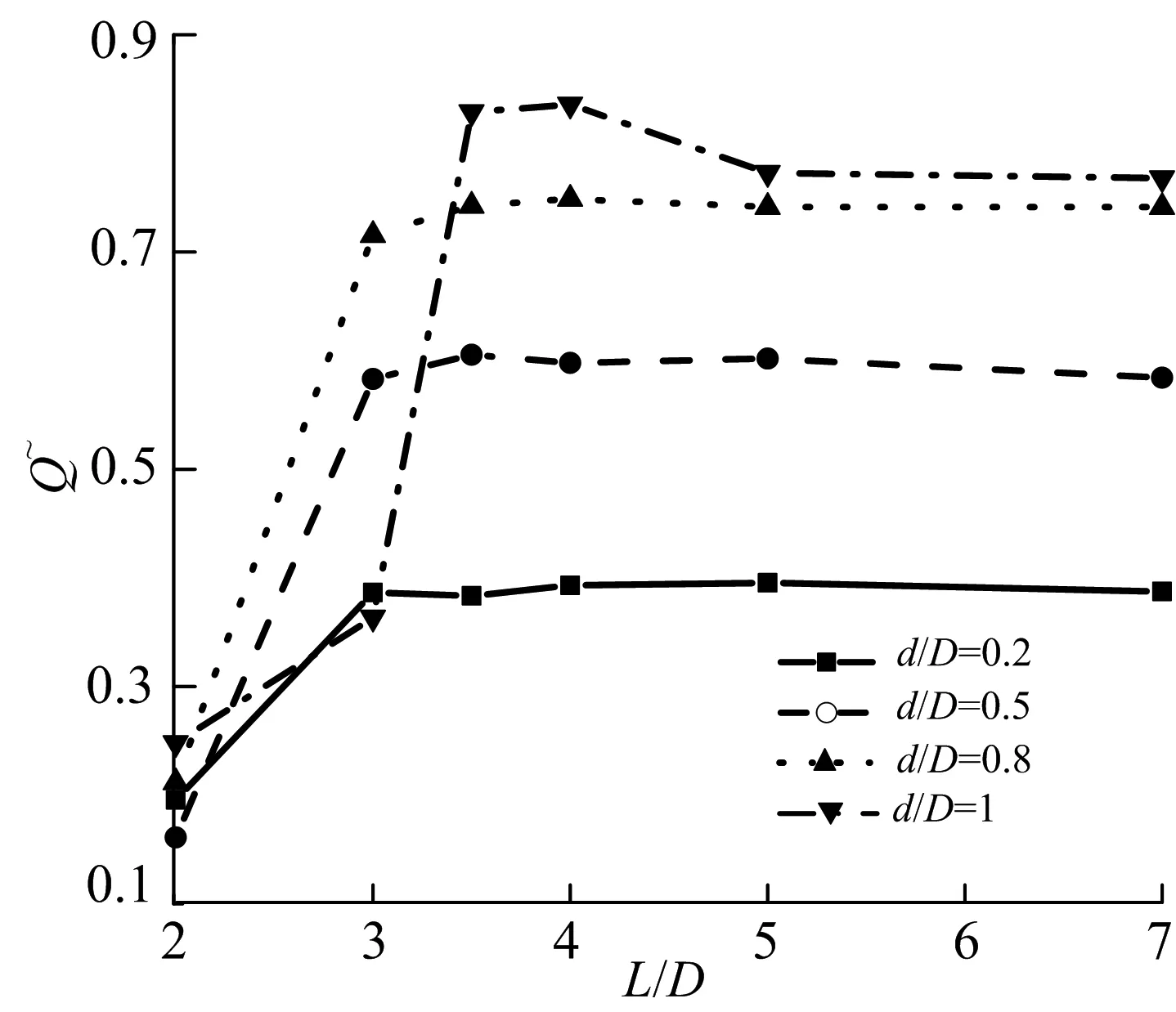
b)ReD=200

由图8和图9综合比较也可发现:在ReD=200的工况下,小圆柱后置并且非常接近大圆柱时(d/D=0.2,L/D=2),系统总热量增长率会达到19.49%,而同时大圆柱的阻力系数下降率为9.44%.这给实际应用带来一个启发,可否在换热器系统中,在每根换热管背风面设置一小圆柱,在某些工况下,尽管会带来体积换热量的增加,蛤同时泵功损耗上升或下降却很小.

进一步研究图8和图9的变化趋势,d/D=0.8和d/D=1的情况比较相近,尤其是在ReD=200的情况下,换热量的增长率几乎是一致的,这就给管束强化换热结构提供了一个新的思路,可适当减小下游圆柱的直径而能够达到等直径圆柱换热的效果.

从两图中都可以看到,在临界距离范围内(L/D=2～3或L/D=3～4),总换热量会急剧增加,这是由于上圆柱旋涡的脱落加强了流体掺混,脱落的流体对后面的大圆柱造成了冲击,同时两圆柱卡门涡街的脱落频率也急剧增大.当然这一现象在d/D=0.2时没有发生,因为此时没有流动型态的转变.而在临界间距比之后(大概为4),换热量的增加就不再显著了,也就是说当间距比大于4,以增加圆柱之间间距来增大换热量就没有意义了.

4 结论

通过对串列双尺度圆柱的绕流换热模拟,得出以下结论:

1)当雷诺数处于100～200范围内,对于串列双圆柱系统,流型转变的临界间距为2～3或3～4之间(因小圆柱位置以及ReD数的不同而不同)，该变化同时引起了阻力系数和换热量的急剧增加，其中,合适的上游圆柱位置可大大减小下游主圆柱的平均阻力系数，但随直径比和间距比的变化,上游圆柱平均阻力系数的变化不大.

2)小圆柱后置较前置情况,对增强系统换热更为有利.模拟发现:对于ReD=200的流动工况,小圆柱后置,并且非常接近大圆柱时(d/D=0.2,L/D=2),系统总热量增长率会达到19.49%,而同时大圆柱的阻力系数下降率为9.44%.

3)当间距比大于4后,换热量的增长率随着间距比的增加变化不大,说明圆柱间距的增大不一定会带来更好的换热效果;将小圆柱位于主圆柱之后时,d/D=0.8和d/D=1两种情况下总换热量增长率很接近,意味着适当减小下游圆柱的直径,也可以达到同等的换热效果.

上述研究为潜在的应用打下基础:在列管式换热器中,有可能采用大小直径的圆柱组合,在体积换热变化很小的情况下达到节约管材耗量的效果.

References)

[1] 米浩君,赵忠超,薛勇，等.流体扰动对不同排列方式下翅片套管换热器换热性能的影响[J].江苏科技大学学报:自然科学报,2014,28(2):150-154.Mi Haojun, Zhao Zhongchao, Xue Yong,et al.Analysis of the heat transfer performance of shell and tubeheat exchanger with different finned array[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition, 2014, 28(2): 150-154.(in Chinese)

[2] Zdravkovich M M.The effects of interference between circular cylinders in cross flow[J].JournalofFluidsandStructures,1987, 1:239-261.

[3] Carmo B S, Meneghini J R, Sherwin S J.Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing[J].PhysicsofFluids, 2010,22: 54-101.

[4] Carmo B S, Meneghini J R, Sherwin S J.Secondary instabilities in the flow around two circular cylinders in tandem[J].JournalofFluidMechanics,2010,644:395-431.

[5] Harichandan A B, Roy A.Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme[J].InternationalJournalofHeatandFluidFlow,2010, 31: 154-171.

[6] Zhou Y, Yiu M W.Flow structure, momentum and heat transport in a two-tandem-cylinder wake[J].JournalofFluidMechanics, 2006, 548: 17-48.

[7] Necati M,Zekeriya A, Numerical investigation of convective heat transfer in unsteady flow past two cylinders in tandem arrangements[J].InternationalJournalofHeatandFluidFlow, 2008, 29:1309-1318.

[8] Iman H, Mohsen S.Numerical simulation of fluid flow and forced convection heat transfer from tandem circular cylinders using overset grid method,[J].JournalofFluidsandStructures,2012, 28:309-327.

[9] Yangyang Gao,Etienne S.Bi-stable flow around tandem cylinders of different diameters at low Reynolds number[J].FluidDynamicsResearch,2011,43:1-11.

[10] Mavridou S G,Bouris D G.Numerical evaluation of a heat exchanger with inline tubes of different size for reduced fouling rates[J].InternationalJournalofHeatMassTransfer,2012,55:5185-5195.

(责任编辑：顾 琳)

Simulationonconvectionheattransferofin-linecylinders

Zhang Donghui, Shi Shan, Wang Jun, Chen Ning

(School of Energy and Power Engineering, Jiangsu University of Science and Technology,Zhenjiang Jiangsu 212003,China)

Unsteady laminar flows passing two in-line isothermal circular cylinders were simulated using the finite element method.The diameter of the large cylinderDwas fixed, while that of the smaller cylinder d varied from 0.2DtoD.The Reynolds numbers based on diameterDwere set at 100and 200.The analysis was carried out for center-to-center spacing ratios,L/D, of 2, 3, 3.5, 4, 5, and 7.The smaller cylinder was placed in front of or behind the large cylinder, with the numerical results validated by literatures.The research shows that, for the in-line dual-scale cylinders, the flow pattern changes when the critical spacing is between 2and 4.The mean drag coefficients of the downstream cylinders is reduced greatly because of the upstream cylinders.But the mean drag coefficients of the upstream cylinders are affected slightly.The heat transfer density is better when the smaller cylinder is placed behind the larger one.Moreover, when the spacing ratio is greater than 4, the system total heat transfer density varies only slightly with changing spacing, and the total heat transfer rate is very close whend/D=0.8 andd/D=1.0,which means it is possible to conserve material consumption for the tube heat exchanger by using cylinders of different sizes while the variation of heat transfer density is slight.

dual-scale cylinders;flow past a cylinder;convection heat transfer

10.3969/j.issn.1673-4807.2014.06.010

2014-08-15

江苏科技大学启动基金资助项目(3501101)

张东辉(1970—)，男，副教授，研究方向为传热传质学.E-mail:dhzhang20@126.com

TK124

A

1673-4807(2014)06-0563-07