探讨递推数列求通项问题
纪宏伟
(如皋高等师范学校,江苏 如皋 226500)
探讨递推数列求通项问题
纪宏伟
(如皋高等师范学校,江苏 如皋 226500)
利用数列的递推关系式求数列的通项公式是数列单元的常见问题,也是近几年高考、模考的热点问题.本文介绍递推数列求通项问题解题策略,并结合高考题和竞赛题验证其具有重要应用价值.
数列;递推式;通项公式
引言
在高考或自主考试中,数列题是压轴题或较难题的题型之一,当它作为压轴题或较难题时,往往结合考查数学思想或数学思想方法,并将函数、导数、方程、不等式等高中数学的主干内容融为一体,呈现出综合性强、知识交叉多、题型变化复杂、思想方法以及能力要求较高的特点.纵览近年来的高考和自主招生试题发现,数列问题如作为压轴题或较难题出现,一般都会具有这么两个特点:(1)命题者通常都会设计一个循序渐进式的“台阶”,第一问为第二问做铺垫,第三问又与前两问有关联,而通常,第一问或第二问一般都是求通项或求和之类问题,至于第三问是什么,有可能是参数取值范围,也有可能是求证不等式,等等,当然,这一问很有难度,目的在于对考生加以区分,但其解题的基础还是前面的台阶;(2)从试题题型模式和基本思路上,具有三式(递推式、通项式、前n项和式)互推形成的“循环推理链”的特点,可用下图来表示:
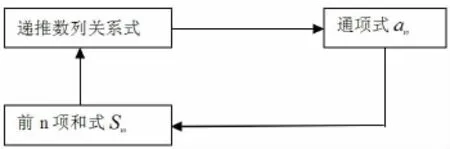
图1 关系图
1 基本递推式和相应方法
1.1 迭加法类型
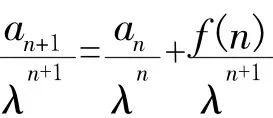
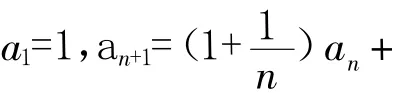
例2在数列{an}中,a1=1,an+1=-an+n2,求an.
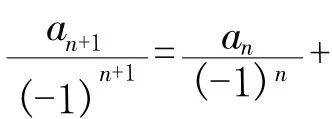
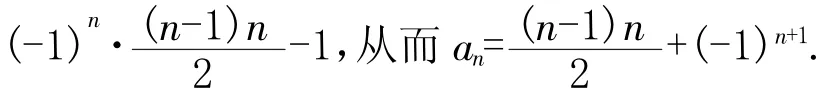
1.2 迭代法类型
例3设{an}是正项数列,a1=1,(n+1)a2n+1-na2n+an+1an=0,求{an}通项.
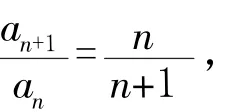
1.3 待定系数法类型
形如an+1=λan+μ(λ,μ是常数且λ≠1,μ≠0)类型,可令a+x=λ(a+x),其中(λ-1)x=μ,x=,从n+1n而构造出一个公比为λ的等比数列{a+}.n
例4已知a1=2,an+1=3an-2,求an.
解 因an+1-1=3(an-1),{an-1}是一个公比为3的等比数列,a1-1=1,所以an-1=(a1-1)·3n-1,即an=3n-1+1.
1.4 特征根法类型
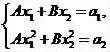
例5数列{an}中,a1=0,a2=1,an+1=an+6an-1,求an.
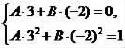
1.5 不动点法类型
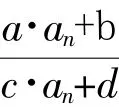
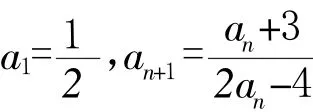
递推数列求通项公式的基本类型用结构图表述如图2所示.
2 可化为基本递推式的处理策略
2.1 两边同时取倒数
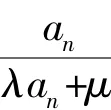
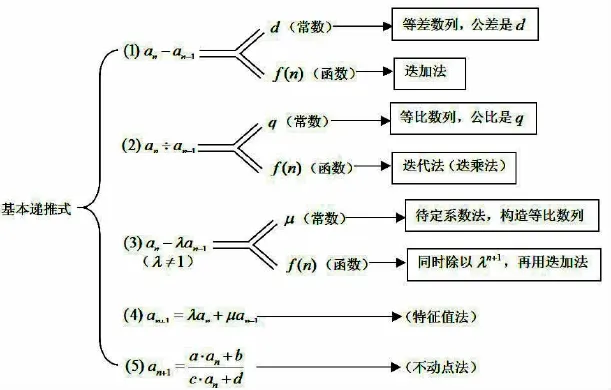
图2 结构图
2.2 两边同时取对数
对于某些根式内是乘积形式的无理递推式,可考虑两边取对数的方法将原式化为熟悉的线性递推式.
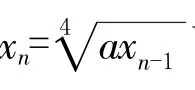
2.3 两边同时除以某一因式
有时通过两边同除因式的方法,再加以简单换元,就能将原式转化为前面所述的基本类型.
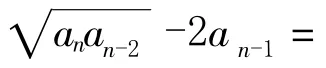
3.4 两边同时添项或常数
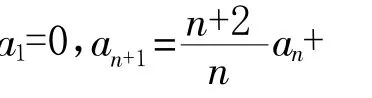
3.5 综合应用
高考、数学竞赛中所给的数列的递推关系式一般都是非基本类型,往往需要策略技巧的综合应用,才可转化为基本类型的结构和模式.
例题11(2010全国大纲卷理科数学压轴题)已知数列{an}中,a1=1,an+1=C-(n=1,2,3…),(1)设C=,bn=,求数列 {bn}的通项式;(2)求使an〈an+1〈3成立的C的取值范围.
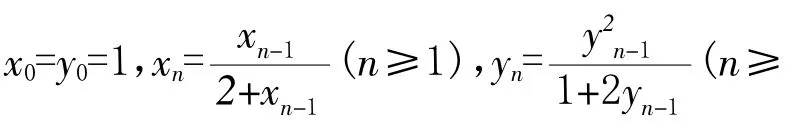
[1]虞 涛.高中课本中的数学基本解题方法[M].上海:华东师范大学出版社,2008.
[2]范端喜.自主招生数学考典[M].北京:北京大学出版社,2013.
[3]雷 波.用不动点法解函数、数列等相关问题[J].中等数学,2008,(10).
责任编辑:张隆辉
O122
A
1672-2094(2014)05-0154-03
2014-06-25
江苏省“青蓝工程”优秀青年骨干教师培养项目(2014),江苏省教育科学“十二五”规划课题“基于概念图的数学教学优化策略研究”阶段性成果(B-b/2013/01/042).
纪宏伟(1977-),男,江苏通州人,如皋高等师范学校数理系讲师,硕士.研究方向:数学教育、泛函分析、信息技术.

