小天体附近的轨道动力学研究综述
于洋,宝音贺西
(清华大学航天航空学院,北京 100084)
小天体附近的轨道动力学研究综述
于洋,宝音贺西
(清华大学航天航空学院,北京 100084)
小天体附近的轨道动力学是现代天体力学的一个重要研究方向,包含着丰富的物理现象和深刻的数学内涵;随着一系列小行星实地探测任务的深入开展,理解小天体附近的轨道运动规律也成为航天领域所面对的众多挑战之一。回顾了小天体研究和探测的历程,分析了小天体附近轨道动力学问题的基本特点和科学价值;详细介绍了航天动力学、行星学和非线性科学三个学科领域对该问题的讨论和研究进展,并列举了各领域中相关的热点问题;基于对上述研究现状的分析,尝试展望了该研究方向未来的发展趋势。
小天体;深空探测;轨道动力学;小行星;非线性
0 引言
对新世界的好奇和渴望,驱使着旅行者们走向远方,开疆拓土,构成了文明进步的原始推动力。现代科技革命,使人类眼中的世界范围空前地扩大了。借助哈勃望远镜,人类早已把目光投向宇宙深处[1];第一艘携带人类信息的太阳系外层空间探测器“旅行者1号”已经飞出了太阳系边缘[2];而“隼鸟号”探测器,则首次成功地将近地小行星25143 Itokawa (中译“系川”)表面的土壤样本送回了地球[3]。在这场目光与脚步的追逐当中,技术的发展无疑是一个关键因素。新的观测设备和探测技术,不仅传回了远方的风景,也让我们得以对赖以生存的太阳系自身进行越来越细致的观察。太阳系小天体的发现和探测,标志着人类对自身生存空间的探索进入了新的阶段,正如美国天文学家Gehrels[4]在1971年做出的著名论断,“从现在起,我们进入了小天体研究的新纪元”。
0.1 小天体研究的历史背景
回顾小天体两个多世纪以来的研究历程,正是人类逐步深入地认识太阳系的最佳指标:两个世纪以前,还没有人知道太阳系小天体的存在,太阳系在人类眼中的图景,只是八个围绕太阳运行的孤独行星;从19世纪早期开始,太阳系小天体逐渐被发现,而当时的人们无法确定它们的数目和质量;19世纪末到20世纪中叶,人类了解到太阳系小天体虽然数目巨大却质量很小,一度忽略对它的研究[5];从20世纪70年代开始,人类对小天体探索的热情再度兴起,陆续开展了许多天文观测与航天探测活动,进行了全面深入的理论研究;迄今为止,人类已经基本确定太阳系小天体的化学组成,初步了解了其内部结构,通过雷达观测获得了多颗小天体的外形,并从探测器传回的图像中提取了少数小天体表面的地形地貌特征[6]。今天我们已经知道,太阳系小天体并不仅仅是漂浮在行星轨道之间的普通石块,其中所包含的丰富信息,足以改变我们对自然科学中一系列基本问题的认识[78]。可以说,有关太阳系小天体近40年的研究历程,清晰地反映了现代科学思想的演变,其中涉及到的学科领域,早已超出天文学的范畴,而且深刻地影响了地质、生物、航天工程乃至武器研究等领域的发展。
太阳系小天体包含除行星和矮行星之外的全部绕太阳运转的天体,其中绝大多数是分布在行星轨道之间的小行星。19世纪初,意大利天文学家Piazzi发现了第一颗小行星1 Ceres,两个世纪过去,人类发现的已编号的小行星超过39万颗,其中95%以上为近20年所发现[9]。随着深空探测技术的发展,人类对小行星的探测,已经从基于地球的观测活动拓展到发射无人探测器到一些特殊小行星进行实地考察。继月球、行星及其卫星之后,小行星已经成为当前深空探测的主要目标之一;开展小行星探测,不仅反映出一个国家在深空测定轨技术、深空轨道优化设计以及航天器自主导航控制等方面的技术实力,更加是综合国力的体现,对于未来国际关系平衡、空间资源共享和空间国防力量的发展必将产生深远影响。
0.2 国内外小天体探测概况
从20世纪90年代开始,美国宇航局(NASA)、欧洲空间局(ESA)和日本宇航局(JAXA)陆续提出各自的小天体探测计划[1011]。
表1给出了这些探测工程的实施(或计划实施)年表。
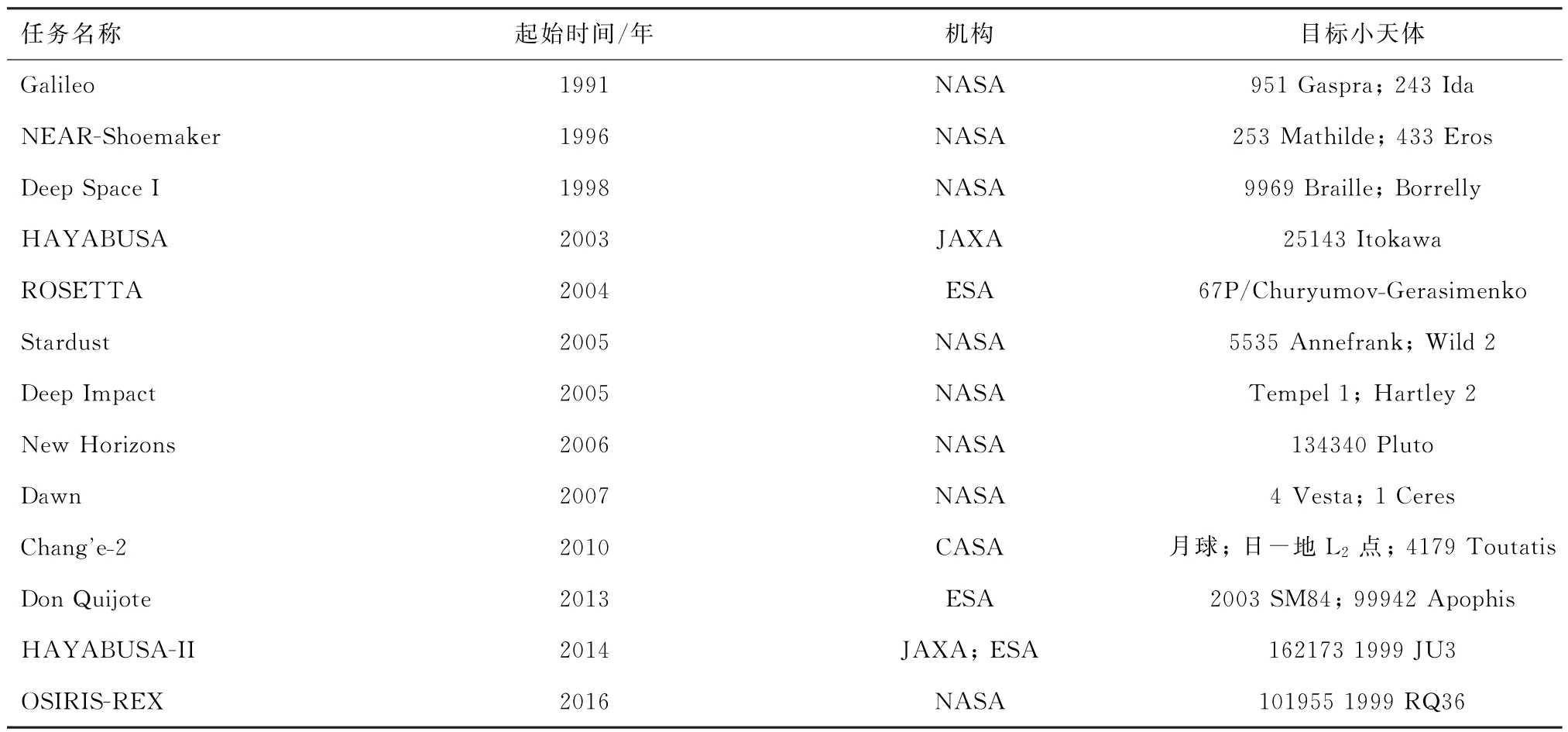
表1 小天体探测任务年表Table 1 Chronology of small body explorations
1991年,美国Galileo探测器在探测木星的途中顺道造访了两颗小行星951 Gaspra和243 Ida,完成了对目标小行星大小、形状、陨击坑的测定;1996年,NASA发射了NEAR-Shoemaker探测器,首次完成了C类小行星253 Mathilde的多谱段拍摄,并在近地小行星433 Eros表面成功着陆;1998年,Deep Space I探测器先后飞越了小行星9969 Braille和彗星Borrelly,完成了彗发等离子体和彗核喷发气流的测定;1999年,NASA发射Stardust探测器,首次成功收集到彗星Wild 2的彗发尘埃样本,并返回地球;2005年,深空撞击计划启动,探测器首先发射撞击器撞击彗星Tempel 1,对弹坑的形状、深度、喷出物进行测量,之后利用地球引力辅助,成功飞越了彗星Hartley 2;2006年, NASA开始实施New Horizons计划,预期在2015年对矮行星134340 Pluto及其5颗卫星进行探测,并在完成之后尝试飞越柯伊伯带天体;2007年,NASA发射Dawn探测器,对主带内最大的两颗小行星4 Vesta和1 Ceres进行探测;另外, NASA预计在2016年开始实施OSIRIS—REX计划,对近地小行星101955 1999 RQ36进行伴飞、接近和采样返回。ESA在2004年启动了ROSETTA计划,预期在2014年接近彗星67P/Churyumov—Gerasimenko并在其表面释放着陆器,对该彗星进行长期监测;随着行星防御问题受到越来越多的重视,ESA在2013年启动了Don Quijote计划,针对威胁地球安全的近地小行星进行一系列新技术的演示和验证。JAXA在2003年发射HAYABUSA探测器对近地小行星Itokawa进行探测,并成功采集了该星表面的土壤样本,于2010年返回地球;它的后续任务HAYABUSA—II也将在2014年发射,计划对C类近地小行星162173 1999 JU3进行探测,并利用爆破设备采集该小行星地下深层样本后返回地球。此外,NASA在2013年提交了一项捕获近地小行星的方案,计划将一颗重约500 t的小行星带入近月轨道,该方案如果通过,将成为航天工程中一项史无前例的创举。
值得一提的是,2012年12月13日,中国的“嫦娥2号”月球探测器在完成既定探月任务之后,成功执行了后续拓展任务,近距离飞越了近地小行星4179 Toutatis,首次获取了Toutatis表面的清晰图像,实现了中国在小天体探测领域零的突破[12]。
0.3 近距离探测小天体的意义
从各国已经完成的小天体探测任务中可以看出,对小天体的实地勘探和深入研究,具有多方面的重要意义。首先,小天体是从太阳系形成之初就存在的“剩余材料”,这些散落的物质没有参与构成行星,却经历了同样长的时间留存至今,由于自身演化的程度比较低,小天体物质相对完整地记录了太阳系早期的条件和状态信息,这些信息都有可能为探寻行星的起源乃至生命的起源提供重要线索[13]。其次,小天体中蕴藏有丰富的工业资源和稀有金属资源,根据计算,1颗直径仅1 km的小行星就可能含有几倍于地球总产量的镍、铂、钴、铱等稀有金属。去小天体采矿,已经作为一个新的工程设想受到广泛的关注和研究[14]。此外,关注小天体的一个更实际的理由是,部分近地小行星可能对行星安全存在巨大的威胁。运行过程中的相互碰撞和空间中各种摄动力的长期作用,都可能促使这些小行星改变轨道,一旦质量稍大的小行星陨落在地球上,对地球生命将是毁灭性的打击。在人类历史上,陨星造成的灾难屡见不鲜,从白垩纪晚期的恐龙灭绝,到20世纪初期的通古斯大爆炸,再到2013年初发生在俄罗斯Chelyabinskaya的陨石伤人事件,都使得小天体的观测和防御受到越来越高的重视[15]。
发射探测器对小天体进行实地考察,对于小天体科学问题的研究,可以提供丰富的细节和直接的证据;对于小天体资源的开发利用,可以在真实环境中对新技术进行演示和验证;对于未来近地小行星的防御,可以提前获得目标的各项参数,以保证防御操作的准确实施。由此可见,近距离探测小天体,其作用和优势是远程观测所不能替代的。
0.4 小天体附近的轨道动力学问题
在技术上,近距离探测小天体是对一个国家深空探测综合技术实力的检验。除去深空测控能力的限制和探测器自主导航技术的要求,仅就探测器的飞行动力学问题而言,就可能因为小天体附近复杂的力学环境而变得异常困难。这些困难会直接反映在探测器的实际飞行当中。例如,2005年11月, HAYABUSA探测器在第二次尝试接近小行星Itokawa的同时,在其表面上空约1.4 km处释放信标和表面探测器MINERVA,结果后者没有按照预定轨迹到达小行星表面。事故分析表明,可能是对该小行星引力场的估计误差所导致的轨道偏差[16]。再如,2011年7月,Dawn探测器进入环绕Vesta的轨道,在此之前的任务设计过程中,美国Planetary Science Institute in Tucson的Tricarico和Sykes (2010)[17]曾指出,探测器与小行星交会过程中,小行星自旋与轨道的共振作用可能造成探测器陷入一个难以依靠自身推力逃逸的区域,此结果被考虑进了最终的接近段轨道设计中,从而避免了危险工况。
从这些实例可以看出,小天体引力场中的轨道力学问题的困难至少来自两个方面:第一,由于测量手段的局限,探测器无法在接近目标小天体之前获得对象的完整信息,特别是目标的运动状态、外形和引力场数据,只能在接近的同时进行测量,经过多次校正之后才能得到对上述参数的准确估计,因而每次接近操作都存在因参数估计误差而导致失败的风险;第二,是问题自身的复杂性,小天体的几何外形、化学组成与内部结构的多样性决定了其附近的引力场可能极不规则,并且具有很强的个体差异,探测器在其中的运动轨道与在行星附近相比有着显著的不同。另外,小天体质量普遍很小,即使考虑在它们附近的轨道运动,仍有可能存在许多不能忽略的空间摄动力,比如太阳及木星的引力、太阳光压力等等,这些因素共同导致了小天体附近的轨道动力学行为十分丰富,而且内在机理迄今并不完全清楚,这对探测器接近段的轨道设计和控制将是巨大的挑战。
可见,探测器在小天体附近的准确运动控制目前仍是亟待解决的技术难点,也是开展小天体探测活动不可回避的研究内容。而准确把握小天体附近的轨道动力学特性,则是工程实现的前提和基础,其对航天任务的重要性已无需赘言。另一方面,太阳系内小天体系统(如双星系统、多星系统)的形成和演化,甚至小天体自身形状、结构和表面性质的演化,都与其附近轨道的运动特征密切相关[1819],研究小天体附近的轨道力学问题,有助于理解这些天文现象的成因,揭示太阳系演化的内在动力学机制。此外,现代非线性动力学的发展,已经为动力系统的局部与大范围行为建立起基本的理论框架,其中涉及许多丰富而有趣的动力学现象,需要在真实的物理系统中寻求验证[20]。质点在小天体引力场中的运动,作为一个真实而复杂的非线性动力学研究对象,为该项研究提供了一个典型的范例,而对该问题的理论探索,将进一步丰富现代天体力学的内涵。
针对小天体附近的轨道动力学问题,不同学科、领域的研究存在多种不同视角。国外大量开展该问题的研究始于20世纪90年代,当时伴随着NASA一系列小行星探测任务的实施,小行星探测器的运动控制、轨道设计、动力学环境分析等问题成为当时航天动力学研究的热点。与此同时,天体力学、行星物理等领域的学者也结合观测结果,就所探测天体的形成与演化过程展开讨论;相应地,以小行星探测为背景,一些特殊引力场中的轨道动力学问题也成为非线性动力学研究的一类重要对象。以下内容中将分别介绍这三个领域对小天体附近轨道的研究进展和热点问题。
1 航天动力学领域的研究进展
小天体附近的轨道动力学问题,本质上是研究一类特殊引力场中的质点运动。航天动力学领域对该问题的探索,从实际应用角度出发,往往首先关注小天体引力场的准确近似方法。
1.1 小天体引力场的近似方法
球谐函数法是描述任意天体引力场的经典方法[21],即在中心引力项的基础上叠加一系列球面调和函数,来描述中心天体引力场的非球形摄动。球谐函数法将计算引力(或引力势)的体积分函数转化为面积分函数,并归结为一系列决定引力场几何性质的球谐系数Cnm和Snm,给出任意引力场在有效半径外部的通用表达形式[22]。由于表达式呈现为各个球谐系数的线性组合形式,探测器在环绕陌生天体飞行过程中,很容易通过飞行数据辨识出各阶球谐系数的值,这也是球谐函数法在航天工程中得到广泛应用的一个主要原因。从20世纪70年代开始,有大量的文献研究球谐系数的反演算法[23- 25]。用传统的球谐函数法来计算小天体附近的引力,主要缺陷在于其收敛性依赖于位置,当所计算的位置接近有效半径时,收敛非常缓慢;当所计算的位置小于有效半径时,则该方法完全失效[26]。对球谐函数法的一个重要改进是最早由Bierly(1897)[27]、Mac Millan(1930)[28]和Hobson(1955)[29]提出的椭球谐函数法,该方法首先建立中心天体的三轴椭球形包络面,根据椭球的三个轴长参数进一步求解谐函数的各阶系数,从而将收敛范围拓展到中心天体附近[30]。显而易见,椭球谐函数法比球谐函数法更胜任小天体附近的轨道动力学的研究。而对于大多数小天体,其准确外形并不清楚,对这类只有基本尺寸的小天体进行研究时,往往采用更直接的方法,把它们视为质量均匀的三轴椭球体,推导引力和引力势的解析表达式[31]。这个方法具有相对简洁的表达形式,便于理论分析;借助成熟的分析方法, German和Friedlander(1991)[32]讨论了旋转椭球体附近可能存在的特殊运动轨道。Li、Qiao和Cui (2013)[33]讨论了均质哑铃型体的平衡点和周期轨道。
对航天任务的分析,通常要求对目标小天体附近引力场进行更加准确的估计,这就需要考虑小天体的具体外形特征。一个直接的思路是,把小天体视为质量均匀的不规则多面体,然后采用经典的引力场体积分处理方法,得到任意多面体的引力表达式(下面称多面体法)。对多面体引力场的研究最早可以追溯到19世纪末[34],而直到近20年,随着计算机技术的迅速发展,该方法才成为计算小天体引力的一个可行方案。Werner(1994)[35]在1993年提出了计算任意多面体外部引力和引力势的闭合表达形式,并在之后在与Scheeres合作的小天体4769 Castalia附近的轨道动力学研究中成功应用了该方法[36]。之后,多面体法在小天体探测任务分析中获得了越来越广泛的应用,与此同时,该方法本身也得到了大量的研究。Forsberg(1984)[37]在1984年提出把任意多面体划分为许多标准的小多面体单元的组合,再对各个单元的引力场分别进行计算和叠加的方法,采用这个方法,可以近似非均质多面体的引力场,实现对真实小天体引力场更精确的近似;Petrovi(1996)和Pohánka(1998)等[38-39]针对多面体引力和引力势的计算公式进行了优化,以更加适合计算机编程;Tsoulis等(2001)[40]还分析了多面体法的奇异性条件。应该说,尽管仍然存在一些问题,多面体法已经成为目前处理小天体探测器轨道运动最为成熟有效的方法。
1.2 接近段探测器的轨道特性
在对探测器运动轨道的研究中,经典的轨道理论和方法,发挥了基础性的指导作用。一方面,摄动方法仍然可以用来分析小天体主要非球形摄动项及其他空间摄动力对轨道运动的影响;另一方面,小天体引力场中的轨道动力学方程与圆形限制性三体问题(下简称限制性三体问题)方程形式非常相近,后者作为天体力学领域的一个核心问题,在过去的一个多世纪里得到了充分的研究和发展,其中涉及的很多方法和规律都可以直接拓展到小天体引力场中的轨道问题。20世纪90年代末Werner(1997)等[36]学者最早开始采用多面体法对一些已知外形的小行星的引力场进行建模,并基于该引力场模型分析了这些小行星附近的轨道运动行为。以雷达观测得到的小行星Castalia模型为例,Scheeres和Ostro等说明了其附近的轨道运动方程存在广义能量积分,并存在类似限制性三体问题中的平衡点、零速度曲面和Hill域;在对赤道面内轨道的研究中,他们发现Castalia附近的同步轨道和顺行轨道都是不稳定的,最终都会逃逸或者坠落,而逆行轨道则大多是稳定的,在实际任务所关心的时间内轨道形状不存在大的变化;同时,基于二阶二次非球形摄动模型,Scheeres等(1996)[41]解析地推出了抛射轨道的存在条件,说明小行星的自旋和轨道角速度之间的共振机制。针对处于复杂转动状态的近地小行星Toutatis,Scheeres等(1998)[42]找到了C20项作用下的一类拟周期冻结轨道,分析了C20和C30项对冻结轨道的综合影响,并在多面体引力场模型下找到Toutatis附近的若干简单周期轨道。这些工作为以后的研究奠定了基础,Hu和Scheeres(2004)[43]基于二阶二次引力场模型研究了赤道面内可能出现的周期轨道;Wang和Xu等(2002)[44]研究了小天体引力梯度力矩对环绕飞行的探测器姿态的影响;Antreasian等(1998)[45]利用二阶二次引力场模型和平均根数法,分析小行星Eros附近的稳定运动,找到一族逆行周期轨道。随着对探测器轨道动力学分析的逐步深入,小天体附近的其他摄动因素也开始被列入考虑,Bottke等(2002)[46]的研究说明了大天体引力、太阳光压都有可能影响探测器轨道的稳定性。
1.3 小天体物理性质和力学环境
小天体在大小、形状、成分和结构上存在巨大的差异,这一直是探测任务实施过程中的一个障碍。几次成功的探测任务传回的数据,使研究人员得以对几颗小天体的动力学性质进行精确的评估,对小天体的一些物理参数的理解也有了长足的进步。Scheeres和Williams等(2000)[47]根据NEAR Shoemaker探测器获得的数据,对主带小行星Eros附近的轨道进行了全面的分析,包括环绕轨道的稳定边界,轨道能量、角动量和平均根数的近似公式,并重点讨论了周期轨道的稳定性条件。研究表明, Eros赤道面附近的逆行轨道并非都是稳定的,而是存在一定参数条件;这个结果在NEAR-Shoemaker探测器的后续任务设计中发挥了重要作用。2005年,HAYABUSA探测器在近地小行星Itokawa附近伴飞了3个多月,获得了高分辨率的小行星形状模型和引力场数据,Scheeres和Gaskell (2006)等[48]基于实测数据对Itokawa附近的真实动力学环境进行分析,讨论了表面坡度的分布、变化和局部重力方向对坡度的影响,计算了表面探测器的最低逃逸速度,并分析了Itokawa附近的平衡点、赤道面附近轨道和极轨的稳定性,准确复现了HAYABUSA探测器一次接近目标表面的轨迹,这不仅说明模型和分析结果的可靠性,也标志着对航天动力学在小天体探测轨道预报方面达到了一个新的水准。Dawn探测器在进行主带小行星Vesta的探测之初,Tricarico和Sykes(2010)[17]利用多种引力场估计模型分析了Vesta附近的1:1共振带,并参考探测器推力限制,预测了可能出现的危险工况,给出了任务轨道的设计原则。由此可见,对小天体附近动力学环境的准确评价和分析,不仅是科学研究的重要内容,更对后续探测任务的实施有重大参考价值。
1.4 接近段轨道设计与控制方法
探测器在小天体附近的运动控制,是轨道动力学研究的主要目标,也是应用研究的前沿课题。无论探测器执行伴飞、悬停、绕飞、着陆(多针对质量较大的探测目标,如Eros),还是接近、附着、采样(多针对质量较小的探测目标,如Itokawa),前提都是对动力学模型和运动规律的正确把握。Broschart等(2005)[49]研究探测器在小天体附近的主动控制策略,分别得到了探测器相对于小天体随体系悬停和相对于惯性系悬停的两种控制律,并通过添加随机摄动,采用数值方法证明了两种控制律在一定参数条件下的稳定性,给出了稳定的临界条件。Antreasian等(2002)[50]详细介绍了NEARShoemaker探测器在Eros表面着陆的设计方案,采用多面体法对引力场进行准确估计,并采用多面体数据近似表面地形,重建着陆场景,复现了4次机动的着陆轨迹。Lantoine和Braun(2006)[51]研究小天体表面的软着陆问题,引入崎岖地形的几何模型,通过求解燃料最优控制问题来得到软着陆控制策略;然后考虑变轨前探测器所处的轨道,分别对小行星Vesta(直径约500 km)和Golevka(直径约500 m)进行分析,发现针对大质量目标Vesta,应当使探测器处于稳定绕飞轨道,而针对小质量目标Golevka,则应当使探测器处于伴飞轨道。除着陆前的轨道之外,着陆点的选择也十分关键,Yano (2006)和Hawkins(2012)[52-53]介绍了实际任务中选择着陆点的一系列约束条件,包括地貌特征、通信和光照条件、科学价值和工程难度等。此外,针对小天体表面探测器的运动问题,Scheeres(1998)等[41,48]分析了不同地形下探测器从表面逃逸的最低速度;Bellerose和Scheeres(2008)[54]则采用三轴椭球体模型,对探测器的运动路径平衡位置和稳定性进行分析,并开发了相应的控制策略,用来约束探测器在椭球表面自由运动的范围。
2 行星科学领域的研究进展
过去20年间,小行星双星系统的大量发现无疑是小行星科学领域中最受瞩目的事件之一。早在两个多世纪以前,Ceres刚刚被发现时,就有人预测小行星可能存在卫星;直到1993年,Galileo探测器首次飞越Ida时发现了它的卫星Dacty1,才证实了这个猜想[55]。迄今为止,人类发现的小行星双星系统已超过200个,这些双星系统的重要性在于,它们提供了小行星的质量和密度信息,也为研究太阳系过去和未来的演化机制提供了重要线索[56]。
2.1 小行星双星系统的轨道特性
借助于雷达观测获得的数据,Scheeres(2002)和Fahnestock(2008)等[5758]研究了双星系统在强非球形摄动作用下的稳定运动轨道,试图理解不规则小天体的卫星可能出现的位置。在此基础上, Scheeres(2002)和Bellerose(2006)[57,59]将全二体问题的数学模型引入双小行星系统(下简称双星系统)的轨道运动研究当中。Maciejewski(1995)[60]给出了全二体模型的绝对运动和相对运动方程,并讨论了可能存在的相对平衡位置;Scheeres(2002)[61]基于椭球—球模型分析了全二体运动的稳定性条件。同时,全二体模型的引力和引力势计算方法也得到了广泛的研究,Borderies(1978)和Braun (1991)[6263]给出了任意两个天体之间引力势的球谐函数表达式,从中可以看出,全二体的球谐函数法存在比单个天体的球谐函数法更严重的收敛性问题[64]。Geissler(1996)和Ashenberg(2005)[6566]给出了更直接的方法,把每个天体按照其外形离散为聚集的质点集合,用全部质点引力(或引力势)之和近似天体之间的引力(或引力势)。Werner (1997)[36]指出,该方法虽然不存在收敛性问题,但是收敛速度非常缓慢,准确计算两个天体之间引力的代价极高。与单个小天体类似,Werner和Scheeres(2005)[67]提出用双多面体模型近似双星系统之间引力和引力势的方法,由于该方法不存在收敛性问题,计算误差被控制在外形的测定误差范围内,所以在之后的双星系统动力学研究中受到重视。Fahnestock(2005)[6768]给出了两个多面体之间引力和引力矩在绝对运动和相对运动方程中的表达式,并针对计算要求对表达式进行了优化。另外,双星系统运动方程的特殊形式,导致了普通的数值积分算法在长时间积分过程中很快失效,Fahnestock和Lee等(2006)[69]提出采用李群变分积分算法求解该方程,使得积分精度获得了明显的提升。采用该技术,Fahnestock等(2006)[70]开发了双多面体模型的运动积分程序,对程序的计算精度和效率进行了检验,并成功应用在近地双星系统66391 1999 KW4的运动分析中[58]。Scheeres等(2006)[71]根据雷达观测得到的数据建立了1999 KW4系统的实际运动模型,仿真结果表明,系统当前的运动状态(主星Alpha高速自旋,从星Beta的运动轨道基本上位于Alpha的赤道面内)主要是由于飞越近日点过程中太阳引力摄动导致的,在当前状态下,Beta的轨道和姿态运动存在较大的波动,并且Alpha的自旋速度接近稳定性极限。这与Walsh等(2008)[72]关于YORP效应导致Alpha在过去几百万年间加速自旋、部分解体而形成双星系统的理论是一致的。
2.2 小天体物质的抛射、撞击与表面地貌特征
小天体自身的演化过程中包含丰富的动力学现象,研究小天体引力场中的轨道行为,对于揭示和了解小天体表面的某些地质特征有重要意义。在漫长的地质演化过程中,小天体会遭受到许多来自陨石的撞击[73],这些撞击对小天体自身的影响并非一瞬间完成,而是要经历相当长的时间才逐渐消退:例如,撞击过程形成的冲击坑,会在各种空间风化机制的作用下逐渐褪化消失[74];撞击过程抛出的物质,一部分直接落回到小天体表面,一部分达到逃逸速度离开小天体,成为空间中的微陨石,其他部分则会暂时围绕小天体运动,成为小天体的临时卫星[75]。这些抛出物质的轨道运动,在20世纪90年代曾得到大量研究[76]。伴随着一系列小行星卫星的发现和NEAR-Shoemaker传回的Eros表面细节图像,人们发现卫星的形成和许多难以理解的地貌特征都可能与冲击过程抛出的物质有关[77], Weidenschilling等(1989)[78]指出,对喷出物轨道动力学的研究,将有助于解开这些谜题。Hamilton (1991)和Burns(1991)[79-80]研究小行星附近轨道运动的稳定性边界,试图解释抛出物围绕小行星运动的稳定性特征。Chauvineau等(1980)[81]研究了太阳引力潮汐对抛出物运动轨道的影响。Richter (1995)和Hamilton(1997)等[8283]研究了距离小行星较远的抛出物的运动特征和稳定性。从1993年开始,Chauvineau等(1993)[84]开始研究小天体附近的动力学环境,基于均质椭球模型讨论喷出物在小天体附近的运动轨迹。这些研究成果表明,小天体附近的动力学环境与行星等大天体存在显著区别。Geissler等(1996)[65]基于探测器得到的Ida动力学模型,模拟Ida表面最大的冲击坑Azzurra抛出物的运动和分布,发现该小行星西北半球表面许多位置的反照率与动力学仿真的结果一致,即回落的抛出物质覆盖在这些表面位置,形成疏松的“风化层”,改变了表面的光学特性。这一成果具有多重意义,首先,它为小天体风化层决定其表面光学特性的猜想提供了直接证据;其次,这个结果间接证明了基于多面体法的轨道动力学模型在研究小天体轨道问题当中的有效性;同时,这是人类第一次对小天体表面发生的一个具体地质事件进行精确的模拟、再现和分析,在一定程度上,标志着太阳系小天体的研究进入了一个精确化的时代。这一研究思路启发和影响了其后的许多工作[85-87]。Durda等(2012)[88]利用NEAR-Shoemaker探测器获得的Eros数据,建立了Eros表面冲击坑抛出物的动力学模型,他们首先从小行星表面图像中识别出大型的抛出物碎块,作为“示踪点”,然后利用轨道动力学程序反向积分求解其运动轨迹,通过与附近的冲击坑进行匹配来识别其来源。通过对“示踪点”的分析,可以基本确定Eros表面风化层的相关力学参数,并了解Eros表面地质形态演化的基本过程。
此外,在行星表面的冲击坑中,“双坑”的比例很高(即两个冲击坑距离很近,形成时间也相同)。对“双坑”成因最有力的猜想是,在与行星交会过程中,单个小行星或双星系统解体,先后撞击在行星表面,由于时间非常接近,导致两个冲击坑距离很近[89]。近20年来,关于小天体系统与行星交会过程中的轨道演化的研究成果不断增多,已经能够部分地解释一些“双坑”的形成和分布,至今仍是行星科学领域的一个热点问题[90]。
3 非线性动力学领域的研究进展
质点在特殊引力场中的运动,是非线性动力学的一类重要研究对象。行星的引力场与质点的引力场近似,经典的摄动方法已经给出了行星附近轨道运动几乎完整的分析;小天体的引力场在几何上则复杂得多,且彼此之间差异巨大,这直接导致质点在其中的轨道行为也极其复杂和多样,其中包含丰富的现象和机制,还远未被充分了解。从20世纪末开始的小天体探测热潮,同样促进了非线性动力学在相关问题上的发展。
3.1 小天体附近的特殊运动集合
一些简单几何体的引力场被视为小天体引力场的抽象近似,研究者们往往把小天体探测作为应用背景,来分析质点在这些引力场中的轨道运动特征。Halamek(1988)[91]提出分布质量的线段可以用来近似一部分扁长型的小天体,给出了线段引力和引力势的计算公式;Prieto-Llanos等(1994)[92]研究旋转的分布质量线段附近的平衡点,分析了平衡点的线性稳定性,并提出一种平衡点镇定控制算法,在火星和火卫一Phobos系统模型下验证了算法的有效性;Riaguas等(2010)[93]进一步研究了这些平衡点的非线性稳定性,应用Arnold的理论方法处理非正定二次型,证明了包括共振情形在内的平衡点邻域内轨道的稳定性[94];Riaguas和Elipe等(1999)[95]考虑系统旋转速度为零的特殊情况,采用数值延拓的方法找到了一系列周期解,并利用Poincaré截面说明周期轨道的混沌与分岔现象。Liu等(2011)[96]将质量均匀的立方体视为一个典型对象进行了系统的研究,讨论了其附近的平衡点、周期轨道并给出了相应的稳定性判据;采用流行拼接的方法找到了平衡点之间的同宿和异宿连接[97];并考虑不同的摩擦系数,计算了立方体表面的平衡区域[98]。三轴椭球体是光学观测中用来近似小天体基本外形的最常用方法[99],而质量均匀的椭球体也常常被用做小天体的基本动力模型。Li等(2013)[33]给出了旋转的椭球体附近的平衡点和稳定性判据,并说明扁圆形小天体引力场中的一些共同的轨道特征;Kammeyer (1978)研究旋转的椭球体附近的周期轨道,并利用Morse引理分析了周期轨道的分岔特征[100]。
在这些研究中,对称性在轨道动力学的分析中起了关键作用,而这正是真实小天体引力场所不具备的特点。Yu和Baoyin(2012)[101]以小行星216 Kleopatra为例,用多面体法计算引力,研究平衡点和平衡点附近的轨道稳定性,试图了解不规则引力场对平衡点附近轨道性质的影响;同样基于多面体引力场模型,他们对Kleopatra的自旋速度和轨道角速度之间的共振情形进行分析,获得了赤道面附近轨道的共振条件,并给出了抛射轨道的分布和边界条件[102]。Yu等(2012)提出了一种不规则引力场中三维周期轨道的全局搜索方案,并以Kleopatra为例说明了引力场的非对称特征对周期轨道族的影响。
3.2 小天体附近轨道运动的几何分析
流形的观点是现代非线性动力学分析的重要思想工具,对动力系统的几何结构的解释,已经深刻地影响了许多领域的发展[104]。在对小天体附近轨道运动的研究中,也有一些工作尝试从这个角度进行探索。Gutiérrez-Romero等(2004)[105]研究分布质量线段周围的平衡点以及附近的不变流形,说明该系统具有Hamilton形式,通过对Hamilton系统的三种李变换,导出了参数化的稳定流形、不稳定流形和中心流形,并且计算得到平衡点邻域内的二维不变环面,发现了该系统的几类周期轨道和拟周期轨道。Jiang等(2014)[106]进一步对不规则引力场中平衡点处的流形结构进行研究。首先介绍了该不变流形的度量的构造方法,给出几类子流形的定义,并依据子流形拓扑结构将平衡点分为8类,给出了对应子流形上的特殊轨道族。
此外,辛几何的思想和方法也被应用到小天体引力场中的轨道动力学问题的研究。由于该问题的一类经典运动方程具有Hamilton形式,Maruskin (2009)和Tsuda(2009)等[107-108]将轨道演化过程的几何不变性应用到该系统的轨道控制当中,设计了一种保辛的状态转移矩阵计算方法,数值验证表明,对比传统的计算方法,该方法给出了状态转移矩阵的更准确的计算结果。
4 结束语
小天体附近的轨道动力学问题,是航天任务中近距离探测小天体不可回避的研究内容和关键的技术难点,在小行星探测任务中扮演着基础和前提的角色;另一方面,小天体系统演化过程中的许多物理现象,都与其附近的轨道运动密切相关,研究小天体附近的轨道动力学问题,可能为理解这些现象找到突破口;此外,小天体附近的轨道运动,为非线性科学提供了一个真实而复杂的研究对象,对该问题的理论探索,可能进一步丰富现代天体力学的内涵。
从探测任务的实际需求出发,精细的动力学模型在小天体探测任务的评价与分析当中仍然具有重要的实用价值,对真实空间环境下小天体附近轨道动力学特性的认知,仍然是理论研究工作的一个重点;从学科创新的角度看,未来应当以小天体探测活动的新任务、新技术为背景,关注其中最近的成果和发现,从中发掘出具有核心性和原创性的新思想,展开系统、深入的研究,既为我国未来的深空探测活动做理论和技术储备,也促进动力学理论的创新和发展。
致谢
本文的部分内容得到国家重点基础研究发展计划(973计划,2012CB720000)国家自然科学基金(No.11372150)的支持,特此表示感谢。
[1] Scoville N,Abraham R G,Aussel H,et al.COSMOS: Hubble space telescope observations[J].ApJS,2007,172: 38-45.
[2] Burlaga L F,Ness N F,Stone E C.Magnetic field observations as Voyager 1 entered the heliosheath depletion region[J].Science,2013,341:147- 150.
[3] Akira T,Masayuki U,Takashi M,et al.Three-dimensional structure of Hayabusa samples:origin and evolution of Itokawa regolith[J].Science,2011,333:1125- 1128.
[4] Bottke Jr W F,Cellino A,Paolicchi P,et al.An overview of the asteroids:the asteroid III perspective[M]∥William F,et al.Asteroids III.Tucson,AZ:Univ.Arizona Press,2002: 3- 16.
[5] Cunningham C.Introduction to asteroids:the next frontier 1st ed.[M].Virginia:Willmann-Bell,1998.
[6] Dankanich J W,Landau D,Martini M C,et al.Main belt asteroid sample return mission design[C].46th AIAA/ ASME/SAE/ASEE Joint Propulsion Conference&Exhibit, Nashville,TN,United States,25- 28 July,2010.
[7] Safronov V S.Evolution of the protoplanetary cloud and formation of the Earth and planets[M].Moscow: Nauka,1969.
[8] Weidenschilling S J.Formation of planetesimals and accretion of the terrestrial planets[J].Space Sci.Rev.,2000,92: 295- 310.
[9] IAU(The International Astronomical Union)Minor Planet Center[OL].[2014-05-01].http://www. minorplanetcenter.net/mpc/summary.
[10] Farquhar R,Kawaguchi J,Russell C,et al.Spacecraft exploration of asteroids:the 2001 perspective[M]∥William F,et al.Asteroids III.Tucson,AZ:Univ.Arizona Press, 2002:367-376.
[11] Cheng A F,Santo A G,Heeres K J,et al.Near-Earth asteroid rendezvous:mission overview[J].Journal of Geophysical Research:Planets,1997,102:23695- 23708.
[12] Zou X,Li C,Liu J,et al.The preliminary analysis of the 4179 Toutatis snapshots of the Chang'E-2 flyby[J].Icarus, 2014,229:348- 354.
[13] 胡中为,徐伟彪.行星科学[M].北京:科学出版社,2008: 334- 365.[Hu Z,Xu W.Planetary science[M].Beijing: Science Press,2008:334- 365.]
[14] Zacny K,Chu P,Craft J,et al.Asteroid mining[C].AIAA SPACE 2013 Conference and Exposition,CA,San Diego, 10- 12 September,2013.
[15] Galimov E M,Pillinger C T,Greenwood R C,et al.The Chelyabinsk fireball and meteorite:implications for asteroid hazard assessment[C].76th Annual Meeting of the Meteoritical Society,Edmonton,Canada,29 July-7 August,2013.
[16] JAXA(Japan Aerospace Exploration Agency)[OL].[2014-05-01]http://www.isas.jaxa.jp/j/topics/topics/2005. shtml.
[17] Tricarico P,Sykes M V.The dynamical environment of dawn at Vesta[M].Planetary and Space Science,2010,58: 12- 38.
[18] Cintala M J,Head J W,Wilson L.The nature and effects of impact cratering on small bodies[M]∥Gehrels T,Asteroids. Tucson,AZ:Univ.Arizona Press,1979:579- 600.
[19] Housen K R,Wi likening L L,Chapman C R,et al. Regolith development and evolution on asteroids and the Moon[M]∥Gehrels T,Asteroids II.Tucson,AZ:Univ. Arizona Press,1979:601 627.
[20] 施尔尼科夫,等.非线性动力学定性理论方法(第一卷)1版. [M].金成桴,译.北京:高等教育出版社,2010.[Shilnikov A L,et al.Methods of qualitative theory in nonlinear dynamics (Pt 1)1st ed.[M].Jin C.World Scientific Publishing Company,2010.]
[21] 刘林.航天器轨道理论[M].北京:国防工业出版社,2004: 109- 113.[Liu L.Orbital theory of spacecraft[M]. Beijing:National Defense Industry Press,2004:109- 113.] [22] Hobson E W.The theory of spherical and ellipsoidal harmonics[M].New York:Chelsea,1965.
[23] Chao B F,Rubincam D P.(1989)The gravitational field of Phobos[J].Geoph.Res.Let.,1989,16:859- 862.
[24] Barnett C T.Theoretical modeling of the magnetic and gravitational fields of an arbitrary shaped three-dimensional body[J].Geophysics,1976,41:1353- 1364.
[25] Jamet O,Thomas E.A linear algorithm for computing the spherical harmonic coefficients of the gravitational potential from a constant density polyhedron[C].2nd GOCE user workshop,GOCE,The Geoid and Oceanography,ESAESRIN,Frascati,Italy,8- 10 March,2004.
[26] Heiskanen W A,Moritz H.Physical geodesy[M].San Francisco:W.H.Freeman and Co.,1967.
[27] Bierly W.An elementary treatise on Fourier's series and spherical,cylindrical,and ellipsoidal harmonics[M]. London:Ginnand Company,1897.
[28] Mac Millan W D.The theory of the potential[M].New York:McGraw-Hill,1930.
[29] Hobson E.The therory of spherical and ellipsoidal harmonics [M].Vermont:Chelsea Publishing Company,1955.
[30] Romain G,Jean-Pierre B.Ellipsoidal harmonic expansions ofthe gravitational potential:theory and application[J]. Celetial Mechanics and Dynamical Astronomy,2001,19: 235- 275.
[31] Dobrovolskis A R,Bruns J A.Life near the Roche limit: behavior of ejecta from satellites close to planets[J].Icarus, 1980,42:422- 441.
[32] German D,Friedlander A L.A simulation of orbits around asteroids using potential field modelling[J].Advances in the Astronautical Sciences,Spaceflight Mechanics,1991,75: 1183- 1201.
[33] Li X,Qiao D,Cui P.The equilibria and periodic orbits around a dumbbell-shaped body[J].Astrophys Space Sci., 2013,348:417- 426.
[34] Rausenberger O.Lehrbuch der Analytischen Mechanik I.B. G[M].Teubner:Leipzig,1888.
[35] Werner R A.The gravitational potential of a homogeneous polyhedron or don't cut corners[J].Celestial Mechanics and Dynamical Astronomy,1994,59:253- 278.
[36] Werner R A,Scheeres D J.Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy,1997,65: 313- 344.
[37] Forsberg R.A study of terrain reductions,density anomalies and geophysical inversion methods in gravity field modeling [M]//Report of the Department of Geodetic Science and Surveying.[s.l.]:Ohio State University,1984.
[39] Pohánka V.Optimum expression for computation of the gravity field of a homogeneous polyhedral body[J].Geophys Prospect,1988,36:733- 751.
[40] Tsoulis D,PetroviS.On the singularities of the gravity field of a homogeneous polyhedral body[J].Geophysics,2001, 66:535- 539.
[41] Scheeres D J,Ostro S J,Hudson R S,et al.Orbits close to asteroid 4769 Castalia[J].Icarus,1996,121:67- 87.
[42] Scheeres D J,Ostro S J,Hudson R S,et al.Dynamics of orbits close to asteroid 4179 Toutatis[J].Icarus,1998,132: 53- 79.
[43] Hu W,Scheeres D J.Numerical determination of stability regions for orbital motion in uniformly rotating second degree and order gravity fields[J].Planetary and Space Science, 2004,52:685- 692.
[44] Wang Y,Xu S.Gravity gradient torque of spacecraft orbiting asteroids[J].Aircraft Engineering and Aerospace Technology,2013,85:8- 8.
[45] Antreasian P G,Helfrich C L,Miller J K,et al.Preliminary considerations for NEAR's low-altitude passes and landing operations at 433 Eros[C].AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Boston,MA,Aug. 10- 12,1998.
[46] Bottke Jr W F,VokrouhlickýD,Rubincam D P,et al.The effect of Yarkovsky thermal forces on the dynamical evolution of asteroids and meteoroids[M]∥William F,et al.Asteroids III.Tucson,AZ:Univ.Arizona Press,2002:395- 408.
[47] Scheeres D J,Williams B G,Miller J K.Evaluation of the dynamic environment of an asteroid:applications to 433 Eros [J].JGCD,2000,23:466- 475.
[48] Scheeres D J,Gaskell R,Abe S,et al.The actual dynamical environment about Itokawa[C].AIAA/AAS Astrodyn. Specialist Conf.Exhibit,Keystone,Colorado,Aug.21-24,2006.
[49] Broschart S B,Scheeres D J.Control of hovering spacecraft near small bodies:application to asteroid 25143 Itokawa[J]. Journal of Guidance,Control,and Dynamics,2005,28: 343- 354.
[50] Antreasian P G,Chesley S R,Miller J K,et al.The design and navigation of the NEAR SHOEMAKER landing of EROS [J].Advances in the Astronautical Sciences,2002,109: 989-1015.
[51] Lantoine G,Braun R D.Optimal trajectories for soft landing on asteroids[J].AE8900 MS Special Problems Report,Space Systems Design Lab,2006.
[52] Yano H,Kubota T,Miyamoto H,et al.Touchdown of the Hayabusa Spacecraft at the Muses Sea on Itokawa[J]. Science,2006,312:1350- 1353.
[53] Hawkins M,Guo Y,Wie B.ZEM/ZEV feedback guidance application to fuel-efficient orbital maneuvers around an irregular-shaped asteroid[C].AIAA Guidance,Navigation, and Control Conference,Minneapolis,Minnesota,Aug. 13-16,2012.
[54] Bellerose J,Scheeres D J.Dynamics and control for surface exploration of small bodies[C].AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Honolulu,Hawaii,Aug. 18- 21,2008.
[55] Chapman C R,Veverka J,Thomas P C.Discovery and physical properties of Dactyl,a satellite of asteroid 243 Ida [J].Nature,1995,374:783- 785.
[56] Richardson D C,Walsh K J.Binary minor planets[J]. Annu.Rev.Earth Planet.Sci.,2006,34:47- 81.
[57] Scheeres D J.Stability in the full two-body problem[J]. Celest.Mech.Dynam.Astron.,2002,83:155- 169.
[58] Fahnestock E G,Scheeres D J.Simulation and analysis of the dynamics of binary near-Earth asteroid(66,391)1999 KW4[J].Icarus,2008,194:410- 435.
[59] Bellerose J,Scheeres D J.Periodic orbits in the full two-body problem[C].The AAS/AIAA conference,Tampa,Florida, United States,22- 26 January,2006.
[60] Maciejewski A J.Reduction,relative equilibria and potential in the two rigid bodies problem[J].Celestial Mech.Dyn.Astr.,1995,63:1-28.
[61] Scheeres D J.Stability of binary asteroids[J].Icarus,2002, 159:271- 283.
[62] Borderies N.Mutual gravitational potential of N solid bodies [J].Celestial Mechanics,1978,18:295- 307.
[63] Braun C V.The gravitational potential of two arbitrary, rotating bodies with applications to the Earth-Moon system [D].Texas:University of Texas at Austin,1991.
[64] Moritz H.Advanced Physical Geodesy[M].Wichmann: Abacus Press,1980.
[65] Geissler P,Petit J M,Durda D D,et al.Erosion and ejecta reaccretion of 243 Ida and its Moon[J].Icarus,1996,120: 140- 157.
[66] Ashenberg J.Proposed method for modeling the gravitational interaction between finite bodies[J].Journal of Guidance, Control,and Dynamics,2005,28:768- 774.
[67] Werner R A,Scheeres D J.Mutual potential of homogenous polyhedra[J].Celestial Mechanics and Dynamical Astronomy,2005,91:337- 349.
[68] Fahnestock E G,Scheeres D J,McClamroch N H,et al. Simulation and analysis of binary asteroid dynamics using mutual potential and potential derivatives formulation[C]. AAS/AIAA Astrodynamics Specialist Conference,Lake Tahoe,CA,United States,7- 11,August,2005.
[69] Fahnestock E G,Lee T,Leok M,et al.Polyhedral potential and variational integrator computation of the full two body problem[C].AIAA/AAS Astrodynamics Specialist Conference,Keystone,Colorado,United States,21- 24, August,2006.
[70] Fahnestock E G,Scheeres D J.Simulation of the full two rigid body problem using polyhedral mutual potential and potential derivatives approach[J].Celestial Mechanics and Dynamical Astronomy,2006,96:317- 339.
[71] Scheeres D J,Fahnestock E G,Ostro S J,et al.Dynamical configuration of binary near-Earth asteroid(66391)1999 KW4[J].Science,2006,314:1280- 1283.
[72] Walsh K J,Richardson D C,Michel P.Rotational breakup as the origin of small binary asteroids[J].Nature,2008,454: 188- 191.
[73] Holsapple K,Giblin I,Housen K,et al.Asteroid impacts: laboratory experiments and scaling laws[M]∥William F,et al.Asteroids III.Tucson,AZ:Univ.Arizona Press,2002: 443- 462.
[74] Mantz A,Sullivan R,Veverka J.Regolith transport in craters on Eros[J].Icraus,2004,167:197- 203.
[75] Thomas P C,Belton M J S,Carcich B,et al.The shape of Ida[J].Icarus,1996,120:20- 32.
[76] Scheeres D J,Durda D D,Geissler P E.The fate of asteroid Ejecta[M]∥William F,et al.Asteroids III.Tucson,AZ: Univ.Arizona Press,2002:527- 544.
[77] Cheng A F,Barnouin J O,Zuber M T,et al.Laser altimetry of small-scale features on 433 Eros from NEAR-Shoemaker [J].Science,2001,292:488- 491.
[78] Weidenschilling S J,Paolicchi P,ZappalàV.Do asteroids have satellites?[M]∥Binzel R P,et al.Asteroids II. Tucson,AZ:Univ.Arizona Press,1989:643- 658.
[79] Hamilton D P,Burns J A.Orbital stability zones about asteroids[J].Icarus,1991,92:118- 131.
[80] Hamilton D P,Burns J A.Orbital stability zones about asteroids.II.the destabilizing effects of eccentric orbits and of solar radiation[J].Icarus,1991,96:43- 64.
[81] Chauvineau B,Mignard F.Dynamics of binary asteroids.I. Hill's case[J].Icarus,1990,83:360- 381.
[82] Richter K,Keller H U.On the stability of dust particle orbits around cometary nuclei[J].Icarus,1995,114:355-371.
[83] Hamilton D P,Krivov A V.Dynamics of distant moons of asteroids[J].Icarus,1997,128:241- 249.
[84] Chauvineau B,Farinella P,Mignard F.Planar orbits about a triaxial body:applications to asteroidal satellites[J].Icarus, 1993,105:370- 384.
[85] Thomas P C,Veverka J,Robinson M,et al.Shoemaker crater as the source of most ejecta blocks on the Asteroid 433 Eros[J].Nature 2001,413:394- 396.
[86] Korycansky D G,Asphaug E.Simulations of impact ejecta and regolith accumulation on asteroid Eros[J].Icarus,2004, 171:110- 119.
[87] Chapman C.Space weathering of asteroid surfaces[J]. Annual Review of Earth and Planetary Sciences,2004,32: 539- 567.
[88] Durda D D,Charpman C R,Merline W J,et al.Detecting crater ejecta-blanket boundaries and constraining source crater regions for boulder tracks and elongated secondary craters on Eros[J].Meteoritics&Planetary Science,2012, 47:1087- 1097.
[89] Bottke Jr W F,Melosh H J.Binary asteroids and the formation of doublet craters[J].Icarus,1996,124:372 391.
[91] Halamek P.Motion in the potential of a thin bar[D].Texas: University of Texas at Austin,1988.
[92] Prieto-Llanos T,Gómez-Tierno M A.Station keeping at libration points of natural elongated bodies[J].Journal of Guidance,Control and Dynamics,1994,14:787- 794.
[93] Arnold V I.Mathematical methods of classical mechanics [M].New York:Springer,2010.
[94] Riaguas A,Elipe A,López-Moratalla T.Non-linear stability of the equilibria in the gravity field of a finite straight segment[J].Celest.Mech.Dyn.Astron.,2001,81: 235- 248.
[95] Riaguas A,Elipe A,Lara M.Periodic orbits around a massive straight segment[J].Celest.Mech.Dyn.Astron., 1999,73:169- 178.
[96] Liu X,Baoyin H,Ma X.Periodic orbits in the gravity field of a fixed homogeneous cube[J].Astrophysics and Space Science,2011,334:357-364.
[97] Liu X,Baoyin H,Ma X.Equilibria,periodic orbits around equilibria,and heteroclinic connections in the gravity field of a rotating homogeneous cube[J].Astrophysics and Space Science,2011,333:409- 418.
[98] Liu X,Baoyin H,Ma X.Dynamics of surface motion on a rotating massive homogeneous body[J].Science China Physics,Mechanics and Astronomy,2013,56:818- 829.
[99] Ostro SJ,Hudson R S,Benner L A M,et al.Asteroid radar astronomy[M]∥William F,et al.Asteroids III.Tucson, AZ:Univ.Arizona Press,2002:151- 168.
[100] Kammeyer P C.Periodic orbits around a rotating ellipsoid [J].Celestial Mechanics,1978,17:37- 48.
[101] Yu Y,Baoyin H.Orbital dynamics in the vicinity of asteroid 216 Kleopatra[J].AJ,2012,143:62- 71.
[102] Yu Y,Baoyin H.Resonant orbits in the vicinity of asteroid 216 Kleopatra[J].Astrophysics and Space Science,2013, 343:75- 82.
[103] Yu Y,Baoyin H.Generating families of 3D periodic orbits about asteroids[J].Monthly Notices of the Royal Astronomical Society,2012,427:872- 881.
[104] 阿诺尔德.经典力学的数学方法.4版[M].齐民友,译.北京:高等教育出版社,2006:iii-v.[Arnold V I. Mathematical Methods of Classical Mechanics.4st ed[M]. Qi M.New York:Springer,2006:iii-v.]
[105] Gutiérrez-Romero S,Palacían J F,Yanguas P.The invariant manifolds of a finite straight segment[J]. Monografías de la Real Academia de Ciencias de Zaragoza, 2004,25:137- 148.
[106] Jiang Y,Baoyin H,Li J,et al.Orbits and manifolds near the equilibrium points around a rotating asteroid[J]. Astrophysics and Space Science,2014,349:83- 106.
[107] Maruskin J M,Scheeres D J,Bloch A M.Dynamics of symplectic subvolumes[J].Siam J.Applied Dynamical Systems,2009,8:180-201.
[108] Tsuda Y,Scheeres D J.Computation and applications of an orbital dynamics symplectic state transition matrix[J]. Journal of Guidance,Control,and Dynamics,2009,32: 1111- 1123.
电话:(010)62773402
E-mail:yuyang.thu@google.com
宝音贺西(1972—),男,教授,博士生导师,主要研究方向:飞行器设计;深空探测动力学与控制。
通信地址:清华大学蒙民伟科技大楼(航天航空学院) N903室(100084)
电话:(010)62795926
E-mail:baoyin@tsinghua.edu.cn
[责任编辑:宋宏]
Review of Orbital Dynamics in the Vicinity of Solar System Small Celestial Bodies
YU Yang,BAOYIN Hexi
(School of Aerospace Engineering,Tsinghua University,Beijing 100084,China)
The orbital dynamics in the vicinity of solar system small bodies(SSSB)is an important aspect of modern celestial mechanics,which has abundant physical phenomenon and may offer a deep insight into the referred dynamics.During last two decades,several deep space probes have been sent to SSSB for in-situ explorations of these small worlds,which highlighted the orbital dynamics in around SSSB as one of the biggest challenges in space engineering.This paper first reviewed the history of SSSB studies and explorations,and gave a summary on the generality and merit of the orbital dynamics.Then we introduced in detail the developments of astronautics, planetary science and nonlinear dynamics on this issue,and presented the relevant hot topics in these fields.Based on the reviews,the last part of this paper attempted to outline the tendency of future researches on this issue.
small bodies;deep space exploration;orbital dynamics;asteroids;nonlinearity
V11
:A
:2095-7777(2014)02-0093-12
于洋(1986—),男,博士研究生,专业:航空宇航科学与技术。通信地址:清华大学蒙民伟科技大楼(航天航空学院) N904室(100084)
2014-05-01
2014-05-20
国家重点基础研究发展计划(2012CB720000);国家自然科学基金(11372150)

