基于约束预测控制的火星大气进入轨迹跟踪
吴超,赵振华,杨俊,李世华,郭雷
(1.东南大学自动化学院,南京210096;2.北京航空航天大学自动化科学与电气工程学院,北京100191)
基于约束预测控制的火星大气进入轨迹跟踪
吴超1,赵振华1,杨俊1,李世华1,郭雷2
(1.东南大学自动化学院,南京210096;2.北京航空航天大学自动化科学与电气工程学院,北京100191)
针对火星着陆任务大气进入段的轨迹跟踪控制问题,给出了一种基于约束预测控制的跟踪策略。综合考虑大气进入段动力学模型的非线性、状态初值的不确定性、控制量限幅约束以及参数摄动,设计了基于线性化阶跃响应预测模型、反馈校正和含约束滚动优化的约束预测控制器,并通过数学仿真对该方法进行了数值验证,结果表明:约束预测控制较PID对参考指令跟踪精度更高,开伞点误差圆半径远小于PID方法;能得到控制量限幅约束条件下平稳的控制曲线。
约束预测控制;火星着陆;轨迹跟踪;线性化预测模型
0 引言
近年来,火星探测已经成为人类向深空探测的最热点目标之一[1]。在未来的火星探测任务中,将火星表面探测定在科学价值更高、地形更复杂的区域,成为必然的要求和趋势[23],这就要求火星着陆器有更高的着陆精度。目前,有两种火星大气进入导引方法:一是采用数值预测—校正技术;二是跟踪参考指令。Korzun等(2010)[4]比较了两种方法:前者无需参考指令,较依赖于模型且需要很高的在线计算能力;后者不依赖于模型,不要求很高的在线计算能力,但是对初值不确定性较敏感,需要设计跟踪控制器予以解决。仿真结果说明跟踪参考指令的方法更适用于火星着陆任务。火星大气进入轨迹跟踪的目的,是在大气进入段引导着陆器到达一个设计好的开伞点。在大气进入段中存在着许多不确定性因素,主要是着陆器初始状态的不确定性和火星大气密度的摄动[58]。为了提高跟踪精度,不少学者尝试设计闭环控制律,其中Bhradwaj等(1998)[5]采用反馈线性化进行火星大气进入轨迹跟踪,在模型准确的情况下精度较高,但是依赖于模型信息,在未知的不确定性因素作用下精度较低;Talole等(2007)[6]尝试了用滑模观测器的办法消除不确定性的影响,精度有所提升,但是由于滑模本身的特点,得到的控制量存在抖动,对倾侧角偏转机构要求较高;Li等(2012)[7]采用了基于指令发生器的直接模型参考自适应方法进行跟踪导引,将开伞点精度进一步提升,但是得到的控制倾侧角仍然具有很大的抖动;Xia等(2013)[8]采用自抗扰的方法进行阻力跟踪,获得了较高的跟踪精度,得到的控制输入无抖动。
约束预测控制(Constrained predictive control, CPC)作为先进控制方法在工业控制过程中得到了不断发展[910]。CPC是基于模型的,能够在允许的模型失配范围内得到优化的轨迹跟踪控制律,具有一定的鲁棒性;CPC还能够处理实际工业控制过程中普遍存在的约束,通过合理选择滚动优化目标函数得到一组变化不剧烈的控制量,从应用角度上讲具有重要意义;CPC还能够容易地处理多变量系统。
基于CPC的方法应用于火星着陆还存在一些困难和挑战,比如如何选取恰当的预测模型、如何选取单输入、多输出模型的滚动优化性能指标式等。
因此,本文围绕如何设计适用于火星大气进入的约束预测控制器进行了一系列研究,首先建立了火星大气进入动力学模型;然后设计了基于线性化预测模型、反馈校正和含约束滚动优化的约束预测控制器;最后进行了仿真研究,仿真结果表明在初值不确定性和参数摄动下,约束预测控制较PID控制有更高的跟踪精度。
1 火星大气进入动力学模型
1.1 MSL型着陆器几何构型
如图1所示,火星科学实验室(Mars science laboratory,MSL)的几何构型为双锥体,前端为减速伞形状。着陆器设计时,使质心偏离自身轴线,从而使质心偏离气动压心,保证着陆器在配平攻角的情况下飞行。
1.2 纵向动力学模型
MSL型火星着陆器的坐标系统如图2所示。
假设火星大气相对于火星静止,并且不考虑外风的影响,则着陆器在大气进入段的纵向动力学模型为[7]
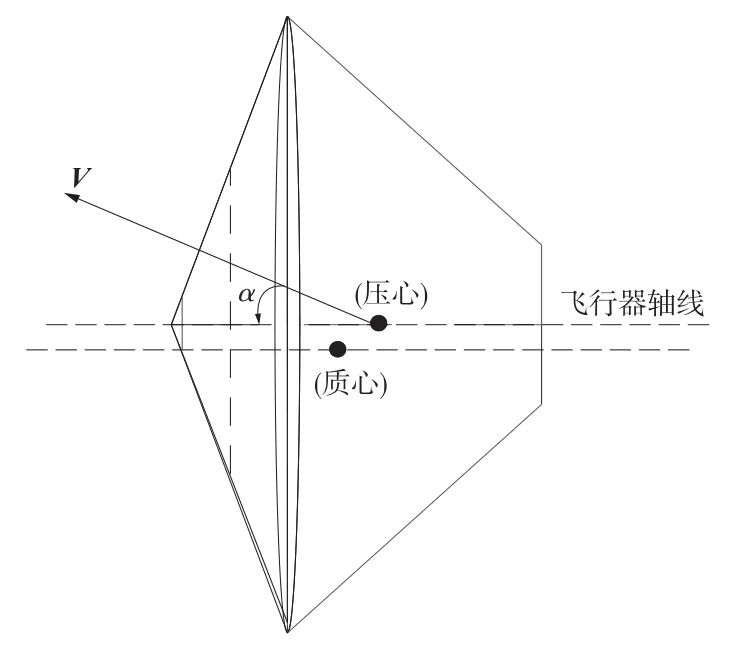
图1 MSL型着陆器的几何构型Fig.1 Geometric configuration of MSL vehicle
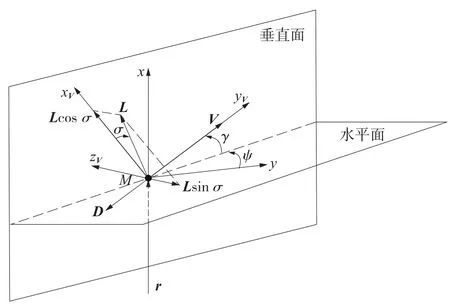
图2 火星着陆器的坐标系统Fig.2 Coordinate system of Mars lander
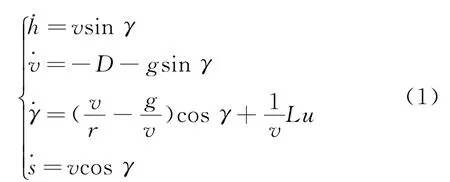
式中,[h vγs]T为状态变量;u=cosσ为控制输入;σ为倾侧角;h和s为位置坐标,其中h为着陆器的高度,s为着陆器的航程;v和γ为速度坐标,其中v为着陆器速度的大小,γ为飞行路径角;r为着陆器质心距火星质心的距离,满足r=h+rM;rM为火星半径;g为着陆器质点处的火星重力加速度,可表示为

式中,μ为火星引力常数;L和D分别为升力加速度和阻力加速度,满足

式中,CL和CD分别为升力系数和阻力系数;Sr为参考面积;m为着陆器的质量;ρ为着陆器质点处的火星大气密度,满足

其中,ρ0为火星表面的大气参考密度;hs为尺度因子。
1.3 着陆器跟踪控制目标
在实际的火星探测工程大气进入段过程中,式(1)表示的动力学模型的初值[h0v0γ0s0]T具有不确定性,并且参数ρ在整个进入过程中存在摄动。在模型存在初值不确定性和参数摄动的情况下,需要设计控制器来跟踪参考指令[hrsr]T;另外,由于控制倾侧角的物理特性,控制量存在限幅约束,并且最好在整个进入过程没有频繁的切换。
2 约束预测控制
一般的动态矩阵控制(dynamic matrix control, DMC)分为预测模型、反馈校正和滚动优化。本文则采用了线性化预测模型和含约束滚动优化,形成约束预测控制来跟踪参考轨迹,如图3所示。

图3 火星大气进入轨迹跟踪控制系统框图Fig.3 Control structure of Mars entry trajectory tracking scheme
2.1 参考轨迹
控制量的参考轨迹可以采用在线快速轨迹规划方法得到,用此优化方法得到控制倾侧角、高度、航程、速度的参考轨迹如图4所示。
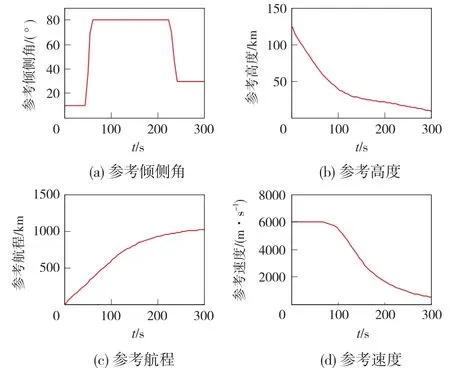
图4 参考控制输入、高度、航程和速度Fig.4 Reference control input,height,downrange and velocity
2.2 线性化预测模型
采用小扰动线性化方法处理式(1)所示的非线性运动方程。
将式(1)写成非线性方程组的一般形式
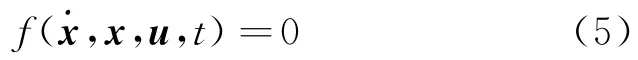
式中,x=[hvγs]T,取
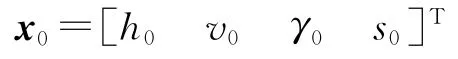
为平衡操作点,将式(5)在平衡操作点处利用泰勒级数展开并保留一次项得

整理式(6)即可得到用增量形式来描述的线性化模型
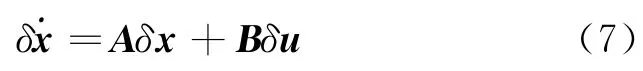
以高度h和航程s为输出,结合式(7)可得线性化的状态空间为

其中,A、B、C为线性化后的状态空间,其中易知

由式(8)表示的线性化模型为单输入、双输出,需要转换为单输入、双输出阶跃响应模型[10]。令s11(t),s21(t)分别为输出y1=h,y2=s对输入u的阶跃响应,并且构成动态矩阵
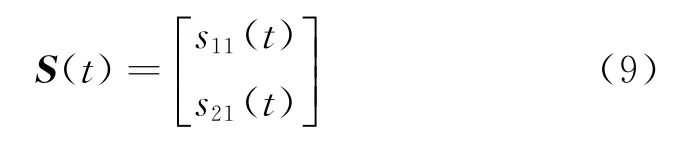
以T为采样周期,N为建模时域,可以得到动态矩阵S(t)的离散时间序列模型
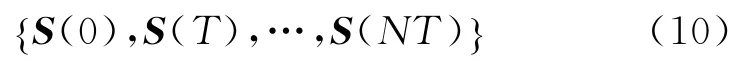
由线性系统的齐次性和叠加性,根据阶跃响应的动态矩阵离散时间序列和控制输入的增量可得预测对象在k时刻的预测输出值

式(11)即式(1)的线性化阶跃响应预测模型,其中j=1,2,…,P,P为预测时域;模型的预测输出为
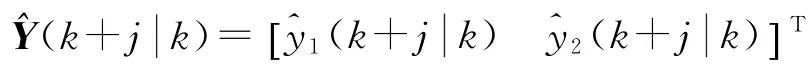
Δu(k+j—i)为k时刻之前的输入序列增量,即“过去的输入”;为k时刻之后的输入序列增量,即“未来预测的输入”。
2.3 反馈校正
由于参数不确定性带来的模型失配以及模型外部干扰等影响,系统的预测输出值需要在预测模型输出的基础上用实际输出来修正。即在k时刻实施控制后,由式(9)表示的阶跃响应预测模型输出和模型实际输出得到经过校正的预测模型输出
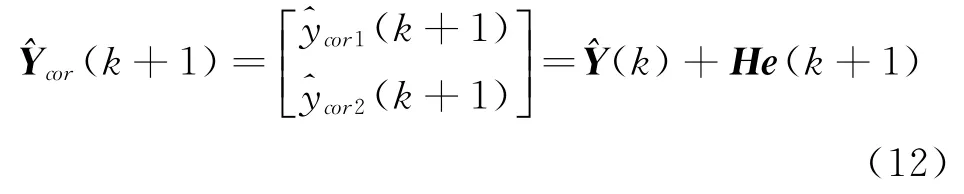
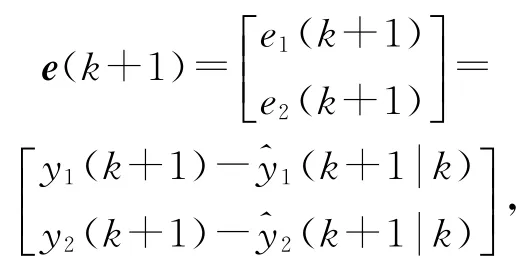
2.4 含约束滚动优化
基于阶跃响应的约束预测控制与无约束预测控制相比,其主要区别是前者增加了硬约束。所谓“硬”约束,即实际工程问题中绝不可以跨越的约束。故约束预测控制不能和无约束预测控制一样通过令性能指标是对ΔUM(k)的偏导数为零解析出最优控制输入ΔUMopt(k),而是需要针对需求构造一个优化命题,再调用通用的二次规划(QP)寻优算法来求解ΔUMopt(k)的数值解序列。
取优化性能指标函数
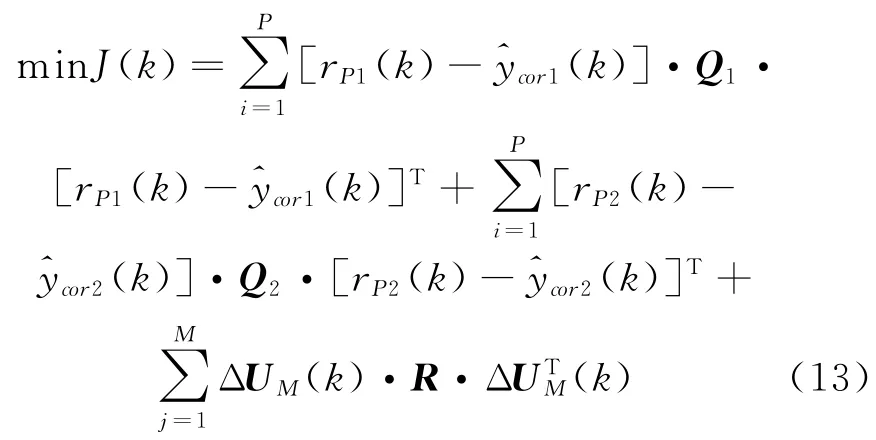
受控制量的限幅约束

其中,rP1(k),rP2(k)为参考模型输出
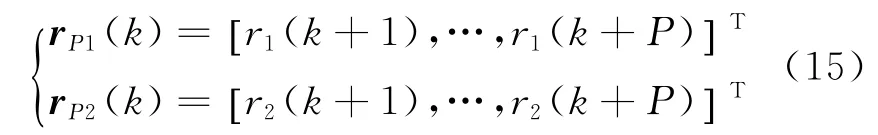

其中,q11,q12,q21,q22,R1均为主对角线元素。然后调用QP算法可解出ΔUopt(k)的数值解。
3 仿真研究
火星大气进入轨迹跟踪仿真分为式(1)表示的控制对象模块和式(11)~(15)表示的控制器模块。
3.1 控制对象模块
模型中所涉及的基本参数取值如表1所示。假设着陆器进入时刻的初始状态不确定性误差服从正态分布并符合3σ原则,如表2所示。除状态初值具有不确定性外,大气密度也存在不确定性。假设火星大气密度摄动15%,误差服从正态分布并符合3σ原则[5]。

表1 火星、火星大气及着陆器参数[11]Table 1 Parameters of Mars,its atmosphere and entry vehicle
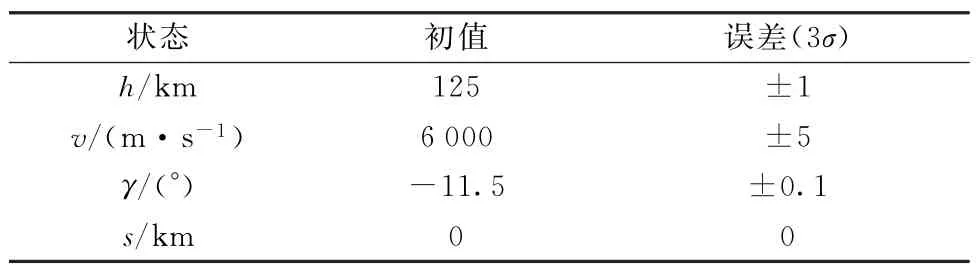
表2 着陆器初始状态及不确定性误差Table 2 Initial states and errors of the vehicle
对运动方程的小扰动线性化结果为

3.2 控制器模块
结合预测控制参数设计理论和工程经验反复试凑,设计出约束预测控制的相关参数如表3所示。本文将约束预测控制的控制结果和传统的PID方法进行了对比,PID参数调节设计如表4所示。

表3 约束预测控制参数设计一览Table 3 Control of parameters of CPC

表4 PID控制参数设计一览Table 4 Control parameters of PID
约束预测控制和PID方法都是在同样的控制限幅下设计的。参数设计时都用到了试凑的办法,在仿真试凑时要兼顾快速性和超调等不同指标,得到相对较优的闭环性能。
3.3 仿真结果
对以上模块进行500次蒙特卡洛仿真,约束预测控制和PID控制下开伞点分布误差如图5和图6所示,约束预测控制下某次不确定性仿真的控制输入、高度、速度及航程如图7所示,此组不确定性参数设置为:h,v,γ的实际初值分别是500 m、2.5 m/s和0.05°,大气密度ρ摄动10%。
对比图5和图6可以发现,在状态初值具有不确定性且大气密度摄动的情况下,实际开伞点大致沿着航向分布,约束预测控制300次开伞点误差圆半径为16 km,而采用传统PID控制的误差圆半径则为95 km。这说明约束预测控制在模型初值摄动、参数摄动情况下对参考指令跟踪精度更高。
图7中的控制输入在限幅约束下曲线平稳,无剧烈抖动的现象,高度误差和航程误差为近1 km和6 km。可见约束预测控制在具有不确定性的情况下,对高度和航程进行了较高精度的跟踪,这是由于约束预测控制基于实际输出对预测输出进行了反馈校正,并且在校正后进行滚动优化得到了控制输入。
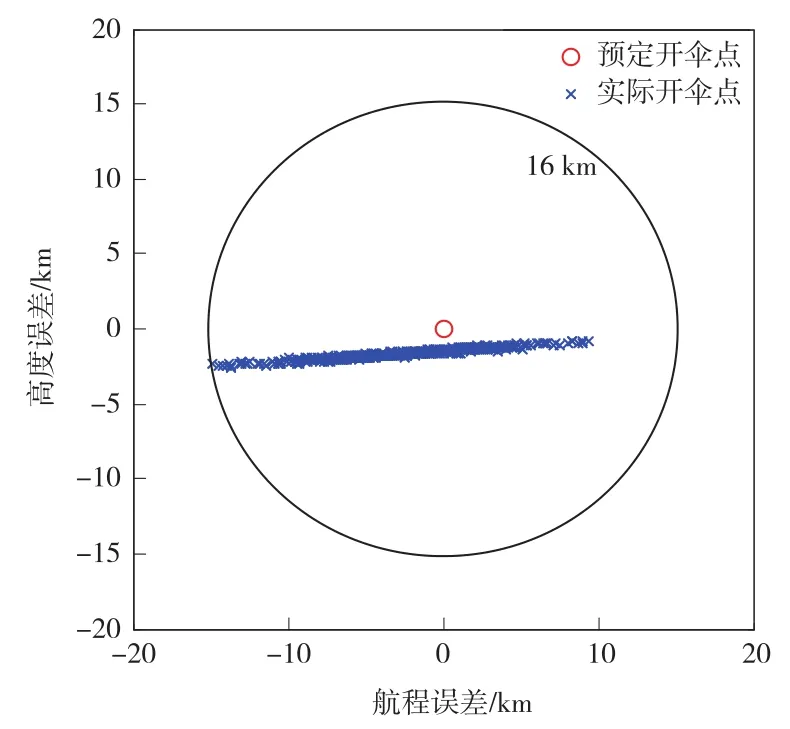
图5 约束预测控制下开伞点分布误差Fig.5 Parachute point distribution error under CPC
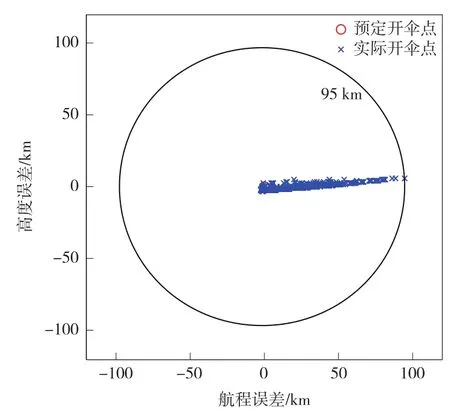
图6 PID控制下开伞点分布误差Fig.6 Parachute point distribution error under PID
4 结论
本文研究基于约束预测控制的火星大气进入段轨迹跟踪控制,主要工作和结论如下:
1)针对火星大气进入段动力学模型的初值不确定性和参数摄动,构建了基于约束预测控制的跟踪控制框架。仿真结果表明,该方法能够以较高的精度跟踪参考指令,开伞点误差圆半径为16 km;
2)对比传统PID控制方法,结果表明,针对初值不确定性和参数摄动,本文的方法具有更高的控制精度,并且能够得到限幅约束条件下平稳的控制曲线。

图7 某次仿真的控制输入、高度、速度及航程Fig.7 Control input,height,downrange and velocity curve
[1] Beaun R D,Manning R M.Mars exploration entry,descent, and landing challenges[J].Journal of Spacecraft and Rockets,2007,44(2):310- 323.
[2] Cheng C C.Development of advanced entry,decent,and landing technologies for future Mars missions[C]∥2006 IEEE Aerospace Conference.Montana,USA:[s.n.],2006. [3] Richard M,Samad H,Gabriel U.Technology development plans for the Mars sample return mission[C]∥2005 IEEE Aerospace Conference.Montana:[s.n.],2005.
[4] Korzun A M,Dubos G F,Iwata C K,et al.A concept for the entry,descent,and landing of high-mass payloads at Mars[J].Acta Astronautica,2010,66(7):1146- 1159.
[5] Bhradwaj S,Rao A V,Mease K D.Entry trajectory tracking law via feedback linearization[J].Journal of Guidance, Control,and Dynamics,1998,21(5):726- 732.
[6] Talole S E,Benito J,Mease K D.Sliding mode observer for drag tracking in entry guidance[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit.Hilton Head:[s,n.],2007.
[7] Li S,Peng Y.Command generator tracker based direct model reference adaptive tracking guidance for Mars atmospheric entry[J].Advances in Space Research,2012, 49(1):49- 63.
[8] Xia Y,Chen R,Pu F,et al.Active disturbance rejection control for drag tracking in Mars entry guidance[J]. Advances in Space Research,2013,53(5):853- 861.
[9] 钱积新,赵均,徐祖华.预测控制[M].北京:化学工业出版社, 2007:2- 16.[Qian J X,Zhao J,Xu Z H.Predictive control [M].Beijing:Chemical Industry Press,2007:2- 16.]
[10] 席裕庚.预测控制[M].北京:国防工业出版社,1993:26- 42. [Xi Y G.Predictive control[M].Beijing:National Defense Industry Press,1993:26- 42.]
[11] Benito M J.Advances in spacecraft atmospheric entry guidance[M].789 East Eisenhower Parkway,USA: Proquest,Umi Dissertation Publishing,2010.
通信地址:江苏省南京市四牌楼2号东南大学中心楼605室(210096)
电话:(025)83793785
E-mail:wuchao7009@126.com
[责任编辑:高莎]
Mars Entry Trajectory Tracking Using Constrained Predictive Control
WU Chao1,ZHAO Zhenhua1,YANG Jun1,LI Shihua1,GUO Lei2
(1.School of Automation,Southeast University,Nanjing 210096,China;2.School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China)
Aiming at tracking the vehicle's entry optimized trajectory for Mars Landing,a new method based on constrained predictive control is proposed.The vehicle's nonlinear dynamics,the initial state uncertainties, saturation limit of the control input and the parameter perturbation are taken into consideration synthetically.A constrained predictive control(CPC)is developed which consists of a linearized step-response predictive model, feedback correction and constrained rolling optimization.The simulation results indicate that:constrained predictive control has a more accurate guidance command tracking performance compared with the PID method,therefore its radius error at the parachute deploying point is far smaller than that of the PID method;a smooth control curve can be obtained under the saturation constraint of the control input.
constrained predictive control;Mars landing;trajectory tracking;linearized predictive model
V17
:A
:2095-7777(2014)02-0128-06
吴超(1988—),男,硕士,主要研究方向:飞行器、导弹、卫星等飞行控制系统的先进控制方法研究。
2014-01-15;
2014-02-27
深空探测973项目(2012CB720003)

