UPFC的选址及网损优化计算

庄海军

(东北电力大学电气工程学院，吉林吉林132012)

电力系统网损计算是确定系统规划、运行、网络改造、设备维修、设备创新的重要依据。电力系统网络损耗与功率在网络中的分布有关，所以控制潮流的合理分布能够减少网络损耗。统一潮流控制器(UPFC)是现今提出的功能最强的FACTS装置，可同时控制母线电压和线路潮流，其安装在网络中的位置决定了潮流分布情况。如何确定UPFC合理的安装位置，选择UPFC最优参数，控制线路传输的功率，对网损优化具有重要意义［1－5］。为此，本文提出基于灵敏度法确定UPFC的最佳安装位置，建立含UPFC的电力系统网损优化模型，并通过改进粒子群算法对模型进行求解，得到最优控制参数，以验证UPFC在网损优化中发挥的作用。

1 UPFC等值模型的建立

UPFC的基本结构为两个由GTO实现的电压型换流器共用一个直流电容构成。UPFC的作用可用电压源的组合来等效，如图1所示。

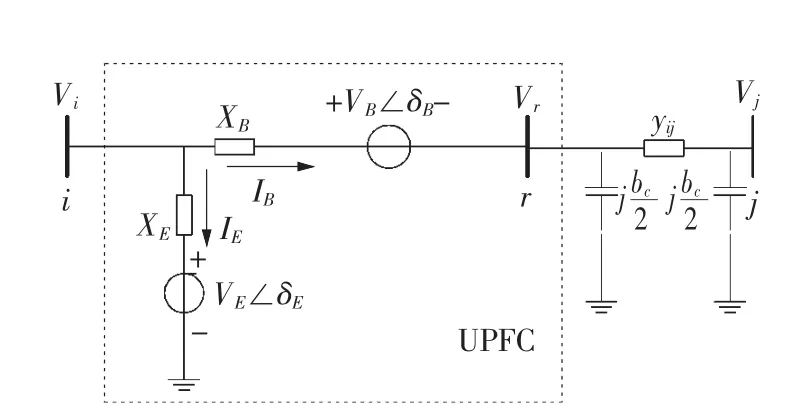
图1 UPFC等效模型Fig.1 UPFC equivalent model

用串联可控电压源VB∠δB和并联可控电压源VE∠δE分别模拟UPFC的串联控制和并联控制部分，可以灵活模拟UPFC的并联、串联补偿和支路潮流控制等功能。并且UPFC电压源模型可以兼顾到变压器的建模和并联侧的有功与无功电流的相互影响，更利于初值的选取。

UPFC加入到线路中改变了网络的结构，为了在潮流计算中可以最大限度地利用传统潮流计算中雅可比矩阵形成的公式和经验，将UPFC对系统的影响移植到线路的两侧节点上，形成改进等效注入功率模型［6］，如图2所示。

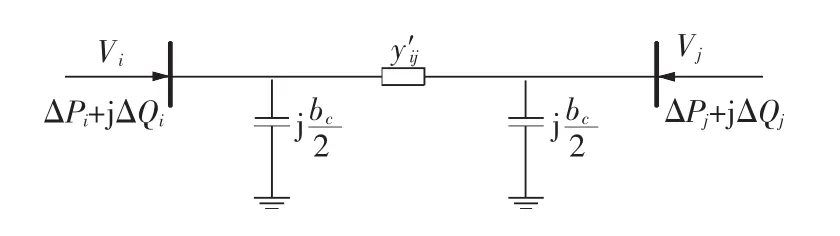
图2 等效注入功率模型Fig.2 Equivalent power injection model

等效注入功率与 UPFC 控制参数 VB、δB、VE、δE之间的关系为

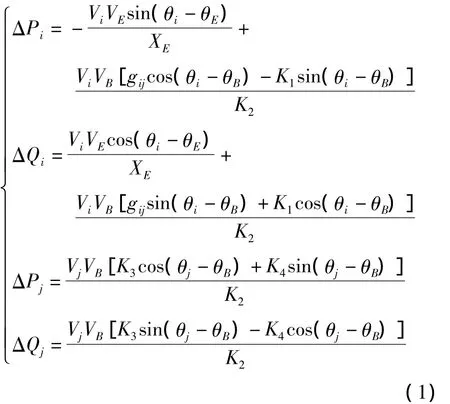
式中

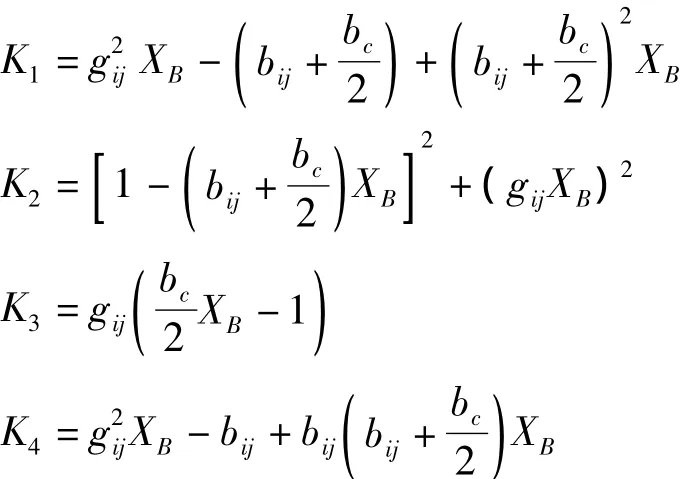
2 UPFC的选址

网络中功率分布和电压不合理，一方面不利于系统电压稳定运行，另一方面也使得网络损耗增大，不利于系统的经济运行。UPFC等效的并联和串联支路对母线电压和线路功率可以起到一定的控制作用，而且UPFC安装在网络中不同位置具有不同的潮流控制效果，若要充分发挥UPFC潮流控制的性能，需将其安装在最佳位置。对于实际系统，不能对每条线路进行仿真测试来确定UPFC最佳的配置位置，故本文在利用模态分析法［7］确定系统薄弱区域的基础上，考虑系统负载能力的潮流方程的灵敏度，根据灵敏度的大小确定UPFC最佳安装位置。

设系统极坐标潮流方程为

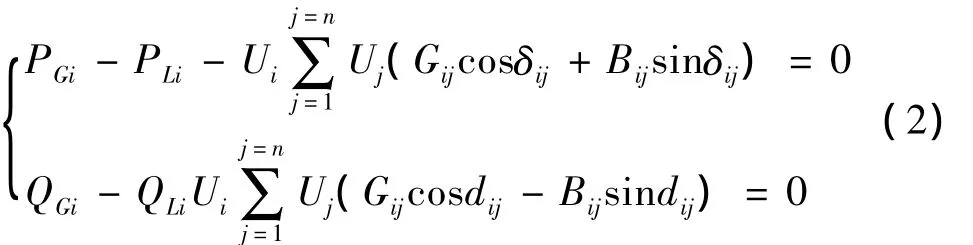
考虑一些动态元件的特性对电压稳定性的影响，可将动态元件的稳态模型修正到常规潮流雅克比矩阵中，根据式(2)就可得到负荷、发电机等静态化的雅克比矩阵:

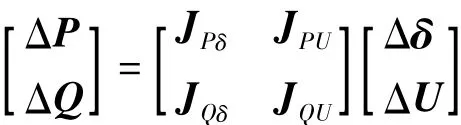
令 ΔP=0，则有

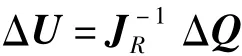
式中JR为系统降价雅可比矩阵，即

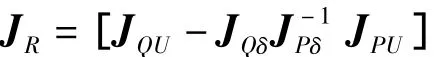
系统电压薄弱的区域可通过JR的特征值与特征向量来确定，即

式中:ξ为JR的左特征向量矩阵;η为JR的右特征向量矩阵;Λ为JR的特征值矩阵。

根据式(3)有

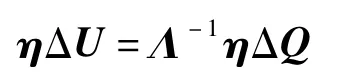
令

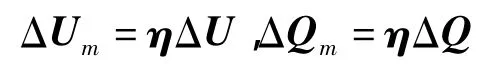
式中:ΔUm为模态电压变化量;ΔQm为模态无功变化量。对第i个模式有

特征值λi越小，表示模态电压受模态无功变化的影响就越大。而节点k的V－Q灵敏度可表示为

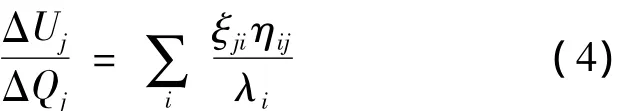
由式(4)可以看出，V－Q灵敏度并不识别单个电压崩溃模式，而仅提供所有模态联合效应的信息。因此，为判别系统薄弱区域，需定义母线参与因子 αji=ξjiηij，其值越大，表明 λi在母线 j对V－Q灵敏度的影响越大，同时表明其线路是较弱的连接线路或是重负荷支路，确定了系统薄弱区域或关键节点。确定系统的电压薄弱区域与关键薄弱节点后，提高该薄弱区域相应线路的负载能力，可有效提高系统输送能力，并改善系统潮流分布。

由式(2)可知，当考虑系统负荷变化与UPFC作用时，系统潮流方程可写为

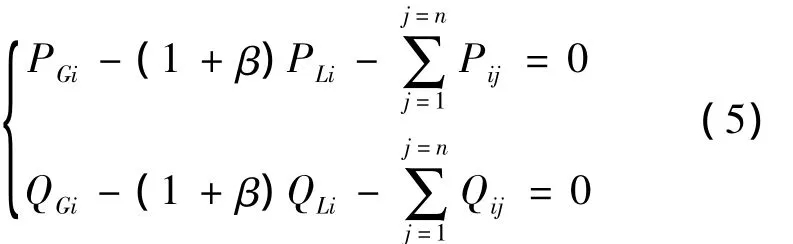
式中:β为负荷影响因子;Pij、Qij为系统的支路潮流。

若忽略UPFC并联部分对系统有功的影响，则可选取负荷影响因子β对UPFC串联参数的灵敏度，根据灵敏度大小判断UPFC对提高支路负荷能力的影响，即

由于主要调节有功功率在网络中的分布，可利用直流潮流计算求出节点注入有功对支路有功Plm的影响系数，即θ=XP，根据其线性特性，有

则节点n注入的有功对支路有功(节点i流向节点j)影响的系数矩阵为

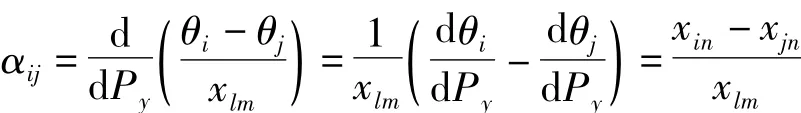
式中:xlm是支路m的电抗;xin、xjn为矩阵X中第i行第n列和第j行第n列的元素。故当支路m为安装UPFC的线路时，该支路的有功潮流为

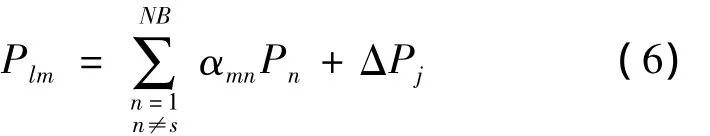
当支路m没有安装UPFC时，有功潮流为

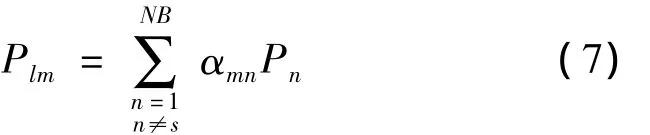
设支路k为安装了UPFC的线路，而m≠k，则根据式(6)、式(7)可知

故根据式(5)则有根据式(1)得到

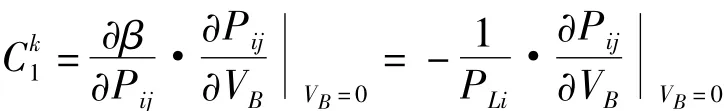
3 含UPFC系统的网损优化

3.1 网损优化数学模型

3.1.1 目标函数

在潮流计算中，只有平衡节点有功功率是未给定的，故全网有功功率损耗最小即为平衡节点注入有功功率最小。当以第n个节点作为平衡节点时，目标函数可写为

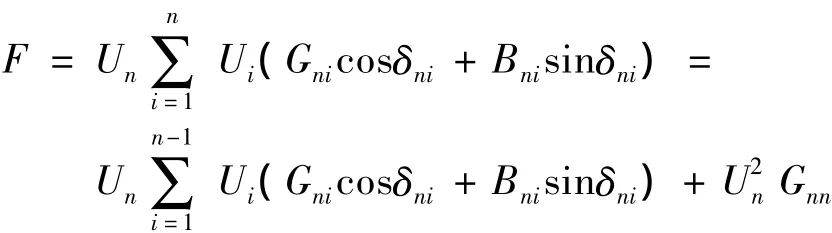
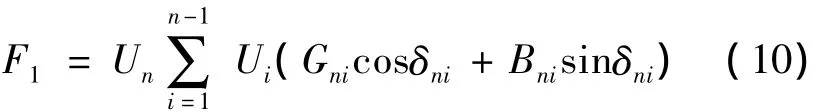
3.1.2 约束条件问题

当系统线路中未安装UPFC时，等式约束为常规的潮流方程，如式(2)所示;当线路装设UPFC后，潮流方程发生变化，如式(5)所示。若认为UPFC内部不消耗有功功率，串联逆变器向系统注入的有功功率PB等于并联逆变器从系统吸收的有功功率PE，即PB+PE=0，由图1UPFC模型可知

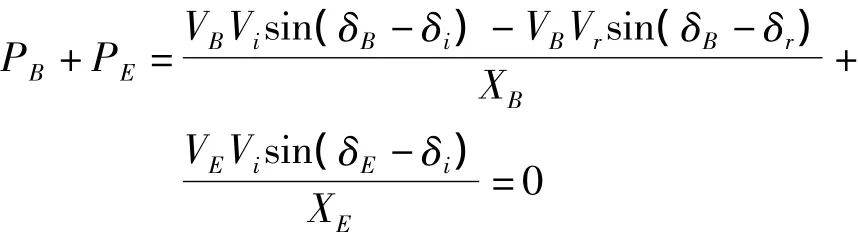
由于 Un、δn、Gnn已知，目标函数可简化为

在不等式约束条件中，不仅包含传统潮流计算电压幅值、变压器变比、电容(电抗)器组数、发电机运行参数等约束，如式(11)所示;还包含UPFC控制变量的约束，如式(12)所示。

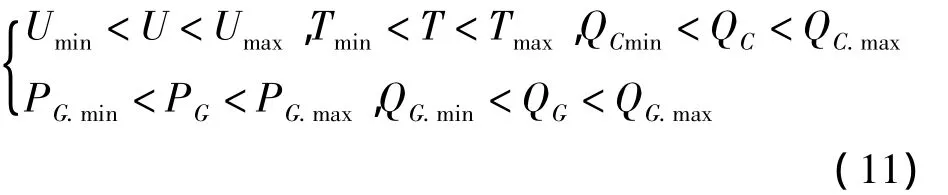
式中:UB.max和 UE.max分别为两个电压源电压的上限;SB.max和 SE.max分别为两个电压源的功率输出上限。

3.2 改进粒子群优化算法

网损优化是通过控制变量的最优组合实现网络损耗最小。粒子群优化算法(PSO)是一种基于种群的随机搜索算法，具有鲁棒性强、搜索效率高、并行性强、控制参数少等优点，在实际工程中表现出巨大的潜力［8］。

在改进算法中对粒子群进行更新时，根据模拟退火算法要求，首先初始化各个粒子的位置和速度。然后评价每个粒子的适应度，并确定初温和退温方式，tk+1=λtk、t0=f(pg)/ln5。最后求取当前温度下的适配值:

式中:U为母线电压;T为有载调压变压器分接头的档位;QC为电容、电抗器组的无功容量;PG为发动机有功功率容量;QG发动机无功功率容量。

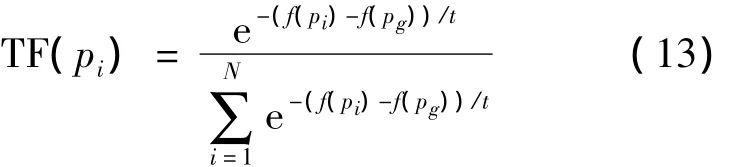
利用一种轮盘赌策略从各个控制变量粒子的位置和目标函数适应度中选取全局最优的粒子代替全局最优解gbest，并根据式(14)、式(15)更新各粒子的位置和速度:

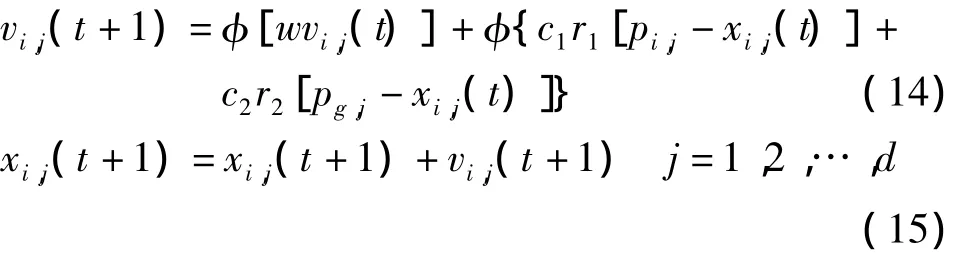
惯性权重w控制粒子的惯性对速度的影响程度，对惯性权重w进行动态处理，可平衡算法全局和局部搜索能力。本文中，w的表达式为

式中:maxDT为最大迭代次数，t为目前迭代次数。

在网损优化中，进化算法需要处理约束优化问题，约束条件的处理至关重要。而PSO算法不具备处理约束条件的能力，缺少有效的处理机制。据此引入可行度策略对约束条件进行特殊处理。

可行度策略是将最优潮流问题的目标函数和约束条件分开处理，目标函数作为适应值函数用来评估解的优劣，约束条件是用来判断解的可行性，可有效避免粒子在不可行域中的搜索，提高了算法搜索效率。比较粒子间的优劣方式为:1)当两个粒子都可行时，比较他们适应度数值f(x)，值小的个体为优;2)当两个粒子都不可行时，比较违背约束程度，程度小的个体为优;3)当两个粒子只有一个可行时，选择可行解。

同时，对各个待优化的变量进行了搜索区域的限制，设置了region数组;对粒子群优化结果进行位置限制，以利搜索最优值，减少迭代次数。

3.3 基于PSO的含UPFC系统的网损优化过程

在改进PSO中，以系统控制变量与UPFC控制变量作为PSO粒子，在求解问题的过程中，利用适应值来评价解的质量，引导优化过程不断进行。选取目标函数式(10)作为算法的适应度函数，因此基于改进PSO的网损优化计算的详细步骤如下:

1)设置系统参数，根据选址程序确定UPFC安装支路号，并指定region数组的上下界值。

2)在满足region条件下，随机赋予种群中控制变量粒子初始值和初始迭代步长;对于每个控制变量粒子，根据目标函数式(10)进行一次计算。

3)评价控制变量的适应值，将控制变量和目标的初始值存储在各微粒的pbest中，将所有pbest中最优控制变量值和目标值存储于gbest中。

4)进入主循环，根据式(16)更新惯性因子w，迭代次数加一次。

5)根据式(13)进行相关模拟退火算法的操作，并根据式(14)计算每个控制变量粒子迭代速度v，若 v≥Vmax，则 v=Vmax;若 v≤ － Vmax，则 v= － Vmax。

6)根据式(15)计算每个控制变量粒子的位置。若控制变量粒子在任一维超出region所设搜索范围，则设置该控制变量粒子的位置为搜索空间的边界值。

7)应用牛顿－拉夫逊迭代法进行一次潮流计算和目标函数计算，再次评估每个控制变量粒子的适应值，并根据可行度准则进行约束条件判断，选取可行粒子。

8)判断是否更新每个控制变量粒子的pbest和整个种群的最优控制变量粒子gbest，进行pbest与gbest粒子更新;判断是否满足算法的停止条件，满足则转向步骤9)，否则转向步骤4)。

9)输出控制变量最优解，即最后一次迭代后的gbest，完成目标函数的计算，求取网络损耗。

4 算例分析

以IEEE－14节点系统为例，确定UPFC的最佳安装位置并进行网损优化计算。其中IEEE－14节点系统取节点1为平衡节点，节点2、3、6、8为 PV节点，节点 4、5、7、9、10、11、12、13、14 为 PQ 节点;可调变压器为4－7，4－9，5－6这三条支路。首先进行潮流计算，并利用模态分析法求出系统母线参与因子，并按大小顺序排出，如表1所示。

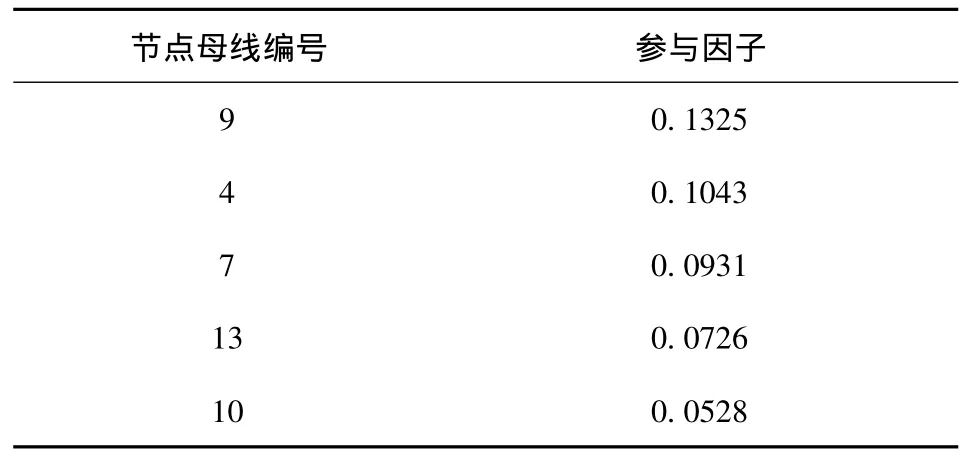
表1 母线参与因子Tab.1 Involved factor of bus node

根据母线参与因子大小确定系统薄弱节点或薄弱区域，并依此计算各支路的灵敏度因子，结果如表2所示。

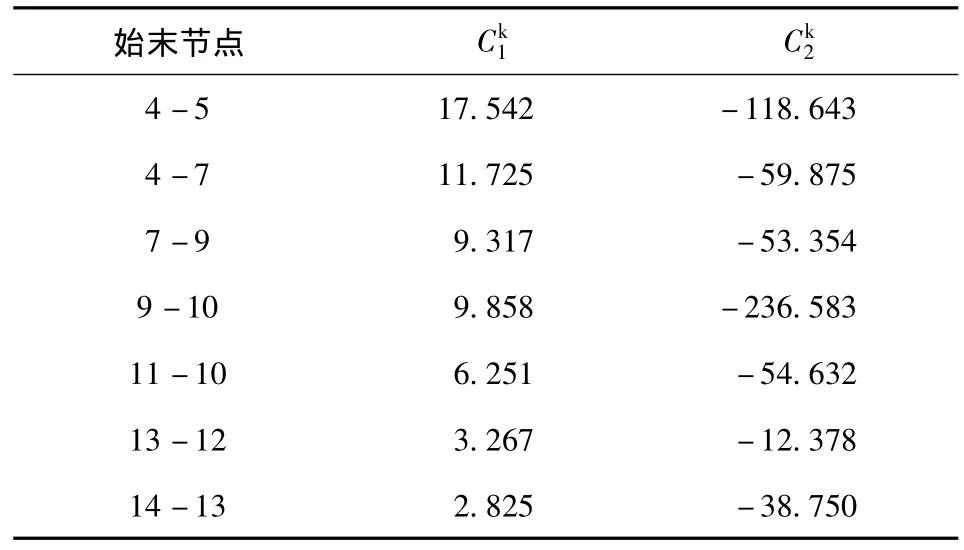
表2 灵敏度计算值Tab.2 Calculated value of sensitivity

在确定了UPFC安装位置的基础上，寻找最优控制变量实现网损优化，其中PSO的参数设置如下:wmax=1.0，wmin=0.5，粒子数目n=40，学习因子c1=c2=2.05，最大迭代次数maxDT=1000。同时，将UPFC电压源模型的初始参数设置如下:VB=0.04、δB= － 90、VE=1、δE=0。计算结果如表3所示。

表3 网损优化结果Tab.3 Optimization results of network loss

由表3可知，利用改进粒子群算法进行含UPFC的电力系统网损优化，当UPFC安装于功率分布较为不合理的线路上时，在改善线路潮流分布、提高系统电压和降低网络损耗方面比安装在其他线路上时的效果更为明显。

5 结语

利用灵敏度判别法确定了UPFC的最佳安装地点，在未破坏网络节点导纳矩阵对称性前提下，建立了含有UPFC的网损优化数学模型，并将改进粒子群算法运用于含有UPFC的网损优化模型的求解中。通过算例计算验证了所建优化模型的正确性，改善了系统电压值，优化了网络的潮流分布，提高了系统的负载能力，实现了网损的优化控制。

［1］ 谢大为.柔性交流输电技术的发展及其应用［J］.电力自动化设备，2007，27(2):16 －19.XIE Dawei.Development and applications of flexible AC transmission systems［J］.Electric Power Automation Equipment，2007，27(2):16－19.

［2］ 周玲，王宽，钱科军，等.计及UPFC的电力系统无功优化［J］.中国电机工程学报，2008，28(4):37 －41.ZHOU Ling，WANG Kuan，QIAN Jun，et al.Power system reactive power optimization considering UPFC installation［J］.Proceedings of the CSEE，2008，28(4):37 －41.

［3］ 李晋园，汤强，向晖.FACTS技术及其在电力系统中的应用［J］.电工电气，2011，10(1):38 －41.LI Jinyuan，TANG Qiang，XIANG Hui.FACTS rechnology and its application in power system ［J］.Electrotechnics Electric，2011，10(1):38 －41.

［4］VURALA A M，TLIMAY M.Mathematical modeling and analysis of a unified power flow controller:A comparison of two approaches in power flow studies and effects of UPFC location［J］.International Journal of Electrical Power ＆ Energy Systems，2007，29(8):617－629.

［5］ VERMAA K S，SINGHB S N，GUPTAA H O.Location of unified power flow controller for congestion management［J］.Electric Power Systems Research，2001，58:89 －96.

［6］ 张扬，毛雪雁，徐政.用于电网稳态和暂态分析的统一潮流控制器模型［J］.电网技术，2002，26(7):30 －33.ZHANG Yang，MAO Xueyan，XU Zheng.UPFC models for power system steady－state and dynamic analysis［J］.Power System Technology，2002，26(7):30 －33.

［7］ GAO B，MORISON G K，KUNDUR P.Voltage stability evaluation using modal analysis［J］.IEEE Transactions on Power Systems，1992，7(4):1529 －1542.

［8］ 黄平.最优化理论与方法［M］.北京:清华大学出版社，2009.HUANG Ping，the editor in chief.Theory and method of optimization［M］.Beijing:Tsinghua University Press，2009.