配电线路感应雷过电压计算

姜玉宏，常 俊

(东北电力大学电气工程学院，吉林吉林132012)

当今架空配电线路绝缘性差，雷电感应过电压(LIV)导致的雷击闪络率很高，占雷击故障概率的90%以上。过去一般采用过电压规程中提供的简单公式对其进行分析，效果不尽人意。近年来，学者更加关注感应过电压的峰值、上升时间等波形参数，对感应过电压数值计算的准确度有了更高的要求。因此分析雷电电磁脉冲产生机理和感应雷过电压的特性对线路防护具有重要的意义［1］。

国外学者很早就对感应过电压的概率分布以及线路闪络次数进行了比较深入的研究。文献［2］提出了一种假设雷电流为直角波计算感应过电压的分布参数电路模型，但是忽略了电场和磁场的耦合;文献［3］提出了电场和磁场相互耦合的传输线模型，但忽略了水平矢量磁位产生的电场;文献［4］在此基础上提出了多导体传输线模型，但该模型基于准TEM波假设，以散射电压对该传输线模型进行激励。对此，为了准确地了解感应雷过电压特性，本文综合考虑以上各模型的优缺点，应用电磁暂态计算程序ATP/EMTP建立一个模拟雷电通道产生的电磁场激励线路过程的模型。该模型可以定义输入与输出量，应用MODELS语言对感应过电压的数值进行求解。

1 模型及计算方法

电磁暂态计算程序ATP－EMTP最初用于对电力传输系统等的暂态仿真，现在广泛应用于雷电暂态过程的分析［5］。MODELS语言提供一种描述模型结构和元件基本功能的格式，允许系统的描述与系统的功能结构相符合，能实现用户自定义的ATP和TACS中现有元件不能实现的功能［6］。

当雷电击中大地时，会在线路附近产生强大的雷电电磁脉冲，电磁脉冲对低压配电线路施以激励进而产生感应过电压。感应过电压的计算首先要建立一个描述云层与大地之间的雷电通道，根据主放电通道的雷电流模型计算出不同空间位置的电磁场分布;再根据线路与电磁场之间的场线耦合模型计算出电磁场在多导体传输线上的感应过电压。

由于雷电放电过程具有很强的随机性和复杂性，创建计算感应过电压的模型基于以下假设:

1)架空输电线路等效为无损传输线，只影响雷电通道产生的水平电场。

2)雷电通道的电荷均匀分布，且垂直于大地。

3)雷电回击速度与光速成一定比例关系且恒定，通道近似于一条理想传输线(TL传输线模型)。

1.1 电磁场计算

根据偶极子理论对Maxwell方程组进行求解，将雷电通道垂直于地面的点作为坐标原点，地面作为x、y平面，主放电通道的中心线作为z轴，如图1所示。

图1 雷电回击通道模型Fig.1 Lightning return stroke channel model

空间任意一点P(r，φ，z)在无损大地上的电磁场表达式为［7］

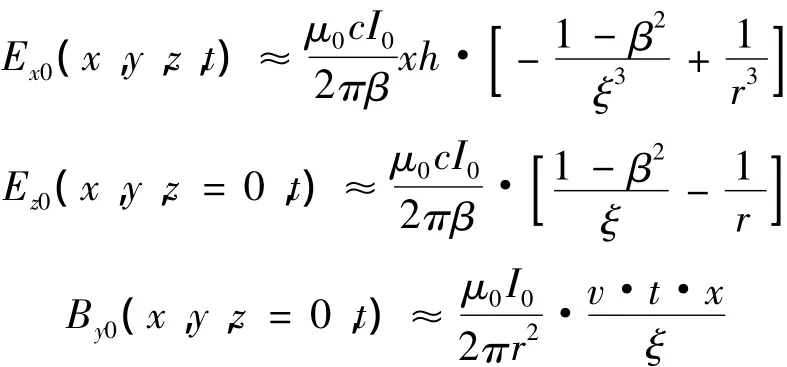
线路的有损部分UΔ(xA，w)为

Cooray－Rubinsten公式考虑了大地电导率对水平电场的影响，且适应于近区域和远区域的电磁场计算，该计算表达式的时域卷积形式为［8］

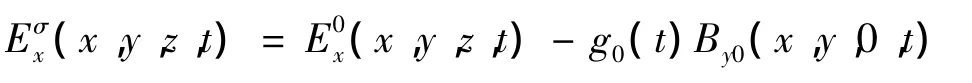
地面损耗g0(t)在频域中的表达式为

式中:c为光速;ε0为空气介电常数;εrg为土壤介电常数;σg为大地电导率。

1.2 空间电磁场与传输线的耦合模型

空间电磁场与架空线路的耦合模型可以通过Taylor模型、Agrawal模型和 Rashidi模型获得。Agrawal模型的时域表达式为

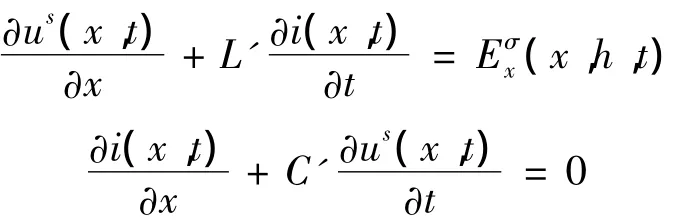
式中:us(x，t)、i(x，t)为传输线上散射电压、感应电流;(x，h，t)为水平电场在高度h处沿传输线方向的分量;L′、C′为传输线单位长度的电感与电容。

雷击点与输电线路的相对位置如图2所示。

图2 雷击点与架空输电线的位置关系Fig.2 Position relation of lightning strike point and overhead transmission lines

在图2中，观测点A为线路的终端，因此xA＞xB，线路高度z=h，此处的感应雷过电压在频域中可表示为

线路的无损部分U0(xA，w)为

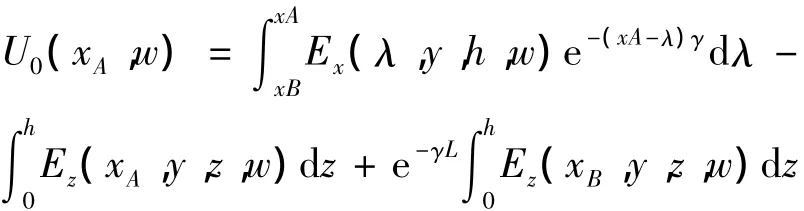
1.3 输电线路等效模型

为了能够应用MODELS语言对感应过电压进行计算，应用经典的Bergeron模型对线路进行建模，如图3所示。

图3 架空线路Bergeron模型Fig.3 Overhead line Bergeron model

UrA(t)其中线路A的终端电压UrA(t)由感应过电压(xA，t)和由线路B端反射的电压叠加而成，延迟传播时间为τ。

上述雷电通道周围电磁场以及感应过电压的计算都是假设雷电流为直角波形，但实际情况雷电流的波形极其复杂，为了简化计算，可以将雷电流波形等效为斜角波，以便对电力系统进行防雷保护设计。雷电流等值斜角波的波形形状g1(t)为

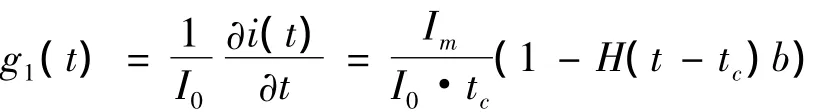
式中:Im为雷电流幅值;tc为到达雷电流波头的时间;b为雷电流波尾响应;H(t)为单位阶跃响应。其中

式中tf为雷电流的波长。

雷电通道对有损大地线路的感应过电压可表示为

其中

1.4 感应过电压仿真模型

应用 ATPDraw搭建如图4所示电路，采用MODELS语言对子模块进行编程计算线路感应过电压，其中输电线路应用EMTP中Type51和Type52进行模拟，阻抗值等于线路的特性阻抗，应用Type60电源等效电压UrA和UrB。

图4 ATP－EMTP仿真计算模型Fig.4 ATP－EMTP simulation model

如果线路终端A和B不在同一水平线上(三相情况)，已知A和B的坐标分别为 (x′A，y′A)和(x′B，y′B)，雷击点位置坐标为(x′0，y′0)，则式(1)可表示为

其中

线路坐标点x需要满足xA＞xB，此时线路长度为L=xA-xB。

1.5 模型验证

为了验证模型计算的准确性，对图5的线路结构进行仿真计算分析。计算条件如下:线路高度为5.68 m;计算中的线路长度为684 m;雷击点距离架空输电线路的水平距离为145 m;雷电回击速度为1.5×108m/s。本文计算的结果与其他方法计算的结果对比如表1所示。

图5 线路结构模型Fig.5 Line structure model

表1 不同计算方法计算结果对比Tab.1 Result Comparison of different calculation methods

由表1可知，本文的仿真计算结果与其他方法计算出来的数据比较接近，在误差允许范围内，因此该模型可以应用到配电线路感应过电压的计算中。

2 感应雷事故仿真计算

架空输电线路附近落雷时，产生的强大电磁脉冲对多导体传输线施以激励，线路产生瞬态感应过电压。图6给出了雷电通道距离架空输电线路的垂直距离分别为20、50、100、150 m 时，感应过电压的波形情况。感应过电压的仿真计算条件为:雷电流幅值为100 kA;雷电流波形为2.6/50 μs;雷电回击速度为1.5×108m/s;线路高度为12 m;大地电导率为0.001 s/m;土壤的介电常数为10;线路长度为1000 m;设雷击点位于线路中部。

由图6可以看出，雷击点与线路的距离越小，雷电产生的感应过电压数值越大。

雷电通道距离架空输电线路的垂直距离为20 m时，不同雷电流产生的感应过电压波形如图7所示。感应过电压的仿真计算条件为:雷电流幅值为100 kA;雷电流波形为2.6/50 μs;雷电回击速度为1.5×108m/s;线路高度为12 m;大地电导率为0.001 s/m;土壤的介电常数为10;线路长度为1000 m;设雷击点位于线路中部。

图6 不同距离感应过电压波形Fig.6 Induction overvoltage waveform in different distance

图7 不同雷电流感应过电压波形Fig.7 Induction voltage waveform about different lightning current

由图7可以看出，感应过电压的数值与雷电流幅值有关，雷电流幅值越大，线路产生的感应过电压数值越大。

雷电通道距离架空输电线路的垂直距离为50 m时，不同雷电回击速度产生的感应过电压波形如图8所示。感应过电压的仿真计算条件为:雷电流幅值为100 kA;雷电流波形为2.6/50 μs;线路高度为12 m;大地电导率为0.001 s/m;土壤的介电常数为10;线路长度为1000 m;设雷击点位于线路中部。

由图8可以看出，感应过电压的数值与雷电回击速度有关，雷电回击速度越大，线路产生的感应过电压数值越大。

3 结论

基于MODELS语言建立的ATP－EMTP模型用于架空线路感应过电压的计算方法，经仿真计算验证，该方法计算结果与其它方法计算的结果在误差允许范围之内，满足了设计要求。同时使用该方法计算感应过电压方便、快捷、可行。

图8 不同雷电回击速度感应过电压波形Fig.8 Induction voltage waveform about different lightning speed

［1］ 边凯，陈维江，李成榕，等.架空配电线路雷电感应过电压计算研究［J］.中国电机工程学报，2012，32(31):191 199.BIAN Kai，CHEN Weijiang，LI Chengrong，et al.Calculation of lightning induced overvoltage on overhead distribution lines［J］.Proceedings of CSEE，2012，32(31):191 199.

［2］ NUCCI C A，RACHIDI F，IANOZ M V，et al.Lightning-induced voltages on overhead lines［J］.IEEE Transactions on Electromagnetic Compatibility，1993，35(1):75 86.

［3］ COORAY V.Calculating lightning-induced overvoltages in power lines.A comparison of two coupling models［J］.IEEE Transactions on Electromagnetic Compatibility，1994，36(3):179 182.

［4］ AGRAWAL A K，PRICE H J，GURBAXANI S H.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field［J］.IEEE Transactions on Electromagnetic Compatibility，1980(2):119 129.

［5］ 陈敏，文远芳，姚宗干.超高压变电站雷电过电压现场实测与仿真计算［J］.电瓷避雷器，2008(6):41 44.CHEN Min，WEN Yuanfang，YAO Zonggan.EHV substation lightning overvoltage field test and simulation［J］.Insulators and Surge Arresters，2008(6):41 44.

［6］ 常俊，姜玉宏.风电场场内输电线路直击雷防护研究［J］.黑龙江电力，2014，36(2):129 132.CHANG Jun，JIANG Yuhong.Research on direct-lightning protection of transmission line in wind farm［J］.Heilongjiang Electric Power，2014，36(2):129 132.

［7］ RUSCK S.Induced lightning over-voltages power transmission lines with specialreference to the overvoltage protection of low-voltage networks［D］.Stockholm:Royal Institute of Technology，1957.

［8］ RACHIDI F，NUCCI C A，IANOZ M，et al.Influence of a lossy ground on lightning-induced voltages on overhead lines［J］.IEEE Transactions on Electro-magnetic Compatibility，2009，51(3):428 442.