含风电场的配电系统可靠性评估研究
杨 劲,肖文成,杨 飞
(广东工业大学 自动化学院,广州 510006)
风能具有无污染、可再生、成本低等明显优势,但它的随机性和不可调度性对电网可靠性和电能质量带来了不可忽视的负面影响。随着风电装机容量和所占比例的增大,尤其是大量新型风力发电机组的投入使用和多个大型风电场直接并入配电网运行,对配电网安全经济运行提出了新的挑战[1]。因此,迫切需要研究多风电场并网后对电力系统供电可靠性的影响,这对电力系统的可持续发展具有重要意义[2]。
考虑到风能的随机特性和风力发电机组强迫停运率等不确定因素,用概率性方法统计风力发电概率成本较为合理。风电接入配电网可靠性分析方法可分为模拟法和解析法,评估含风力发电的系统可靠性指标时,模拟法具有足够的可行性,而解析法不能很好地模拟风速随时间的随机变化和反映真实系统运行状态,适用于电力系统的规划研究。文献[3]分别运用了序贯蒙特卡罗法和解析法计算风电场容量可信度,并提出在模拟复杂系统的统计分析中蒙特卡罗模拟法更加适用。文献[4-5]计及气候因素对配电网可靠性的影响,采用了蒙特卡罗法模拟天气的随机变化进行分析建模。文献[6]运用FMEA计算了含多风电场的地区电网可靠性指标,但它未计及气候因素对元件故障率的影响。
本文从普通配电网可靠性评估入手,在综合分析各种影响配电系统可靠性评估精度的因素基础上,建立了计及开关元件拒动和元件气候因素的两状态可靠性参数修正模型,将此模型和FMEA法应用于含风电场的配电系统可靠性评估中,研究了基于孤岛模式下的含多风电场的配网系统可靠性,并根据孤岛划分模型将系统负荷划分为孤岛内和孤岛外,研究了不同孤岛划分对系统可靠性的影响。
1 风电场的可靠性模型
由于风速的随机性,可以把风电场出力等效为在0~Pmax之间变化的随机函数[7-8]。风电机组出力Pt与风速Vt的关系可由下式近似表示:

式中:Pt为风电机组出力;Vi、Vr和Vo分别表示风电机组的切入风速、额定风速、切出风速;Pr为风电机组额定功率;参数a、b的表达式为
根据风速大小的统计学规律来描述一个地区风速大小的分布函数有很多,但普遍认为威布尔(Wei-bull)分布双曲线[9]最适合用于描述风速统计的概率密度函数,其表达式为

式中:v为作用在风力机上的风速;k和c分别为威布尔分布的形状参数和尺度参数。
根据式(1)可以得出风力发电机的输出功率为P时的概率密度函数[10],其表达式为

此概率密度函数为一个分段函数,其函数曲线如图1所示。
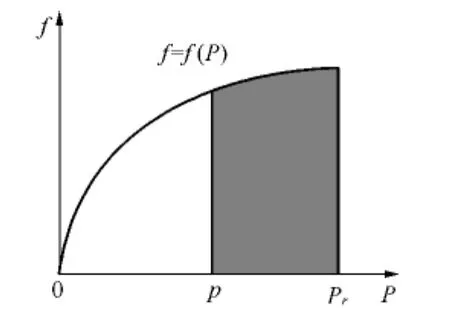
图1 风力发电机输出功率对应的概率曲线Fig.1 Probability curves corresponding wind generator output power
当只有风电机组对负荷进行供电时,负荷为p,风电机组若满足负荷需求,就必须要求其输出功率大于负荷p,也就是其输出功率要落在图1所示的阴影部分区域内,这部分风力发电机的供电概率为

2 配电系统可靠性指标
配电系统可靠性是指供电点到用户,包括变电所、高低压线路和接户线在内的整个配电系统及设备,按可接受标准及期望数量满足用户电力及电能量需求能力的度量[11]。系统可靠性主要指标如下:
系统平均停电频率指标为

系统平均停电持续时间为

用户平均停电持续时间为

平均供电可用率指标为
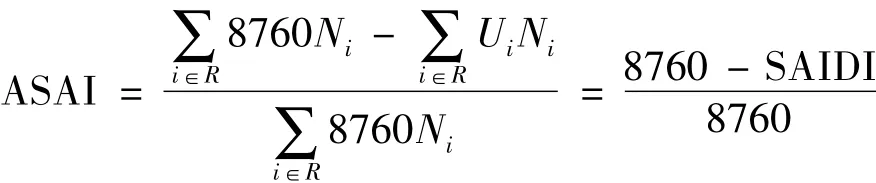
系统缺供电量指标为

式中:λi和W1、W2和W3分别为负荷点i的用户停运率和用户数;Ui为负荷点i平均年停运时间,h/a;Pai为负荷点i的平均负荷,kW。
负荷侧可靠性指标如下:
用户平均停电时间为
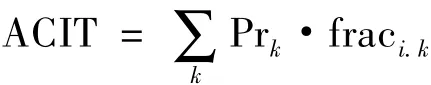
用户平均停电频率为

平均停电持续时间为

式中:Prk为故障k发生的概率;fraci.k是故障i,k的相关系统,0 ≤ fraci.k≤ 1。
3 元件的气候两状态等效模型
在传统可靠性评估中,未考虑暴风雪、冰冻、咫风等灾害气候对电力系统可靠性的影响,其可靠性预测结果不符合实际情况,存在很大误差。现实数据统计表明,元件故障发生在恶劣天气的概率相比正常天气大的多。因此,在电力系统可靠性评估中考虑天气变化对可靠性的影响十分必要[12]。
将天气变化等效为正常天气和恶劣天气的随机过程,在时间T内天气随机变化的情况如图2所示。

图2 天气随机变化图Fig.2 Stochastic weather change diagram
正常天气的期望持续时间为N=∑ni/T,恶劣天气的期望持续时间为S=∑Si/T。统计时间T内正常天气和恶劣天气期望时间值如图3所示。
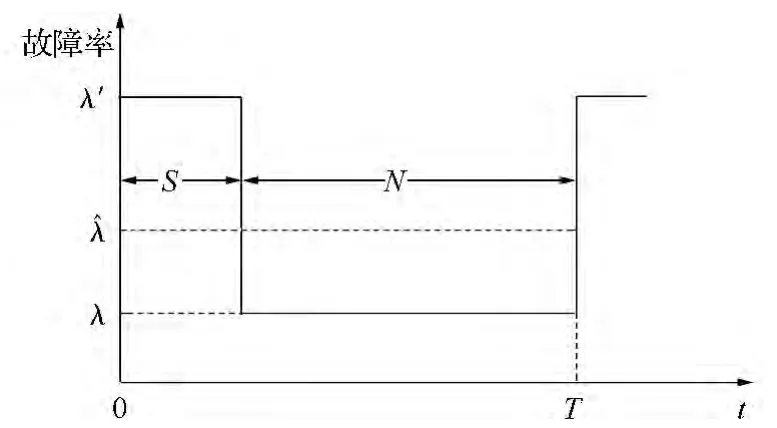
图3 统计时间T两种天气持续时间的期望值Fig.3 Two weather duration expectations in statistical time T
元件的平均故障率可以表示为
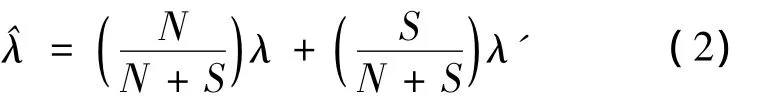
设恶劣天气下发生故障的概率为0≤F≤1,则由式(2)可知

本文采用蒙特卡罗模拟方法,对元件所处的天气状况随机抽样,建立相应的元件气候等效模型。
4FMEA法原理
FMEA法是解析法中最经典的方法[13],FMEA法根据选定的可靠性准则将配电系统划分为故障状态和正常运行状态,然后根据各种预想故障状态对系统产生的可靠性影响,计算出相应的可靠性指标。在分析过程中,一般以连续性作为准则,供电连续性遭到破坏即为故障状态,否则为正常。FMEA法具体流程是:首先根据系统的网络拓扑结构图建立故障模式影响分析表,分析各个元件故障概率及停运时间并确定该故障的影响范围;然后做出综合考虑分析;最后计算出系统和负荷点的可靠性指标。FMEA法的流程如图4所示。典型的FMEA分析法的故障模式影响分析表如表1所示。
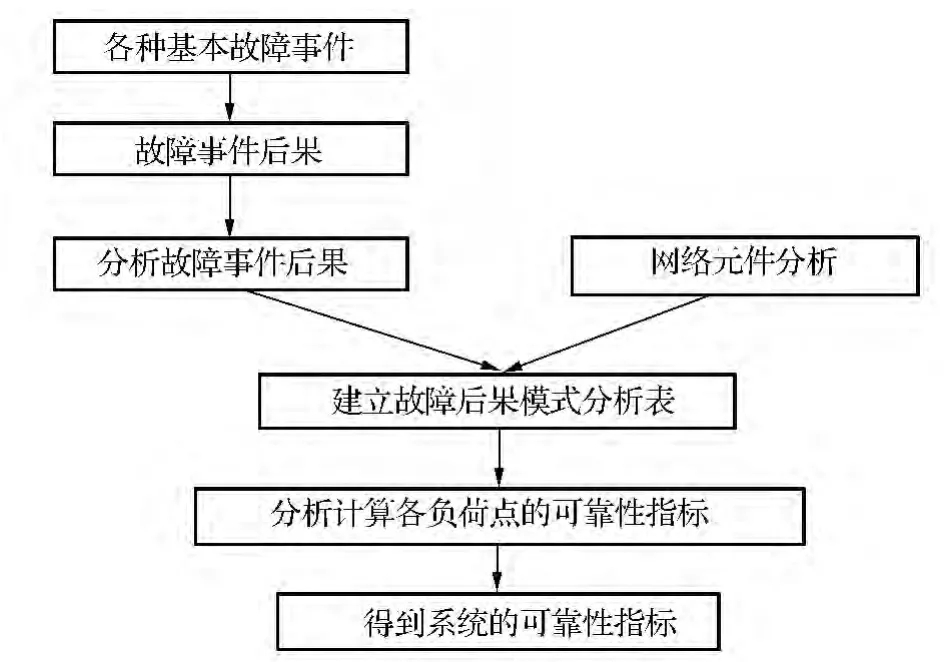
图4FMEA法流程图Fig.4 FMEA method flow diagram

表1 典型FMEA分析表Tab.1 Typical FMEA analysis table
5 IEEE RTBS算例分析
5.1 算例数据
采用 IEEE-RBTS Bus6[14]系统为展开可靠性评估研究算例模型,该系统包括30段线路、23个负荷点、23个熔断器(装设在各负荷支路首端)、21个隔离开关、23个配变、4台断路器和1183户用户,如图5所示,其中隔离开关操作时间为0.5 h。
5.2 研究方案及结果分析
5.2.1 不含风机的配电网可靠性评估方案研究
方案1:不接入风电场,不计断路器和熔断器拒动的概率,不考虑气候因素对元件故障率的影响。
方案2:不接入风电场,计及断路器和熔断器拒动的概率,不考虑气候因素对元件故障率的影响,假设断路器和熔断器拒动的概率为0.1。

图5 RBTS-BUS6配电系统接线图Fig.5 RBTS-BUS6 power distribution system wiring diagram
方案3:不接入风电场,不计断路器和熔断器拒动的概率,考虑气候因素对元件故障率的影响,假设全年正常天气241 d,坏天气124 d,故障发生在坏天气的概率为0.75,生成相应的故障率天气模型,分析气候因素对配电系统的影响,修正后的元件故障参数如表2所示。
将上述3个方案计算结果汇总分析,3种方案下部分负荷点指标如表3所示,系统可靠性指标如表4所示。
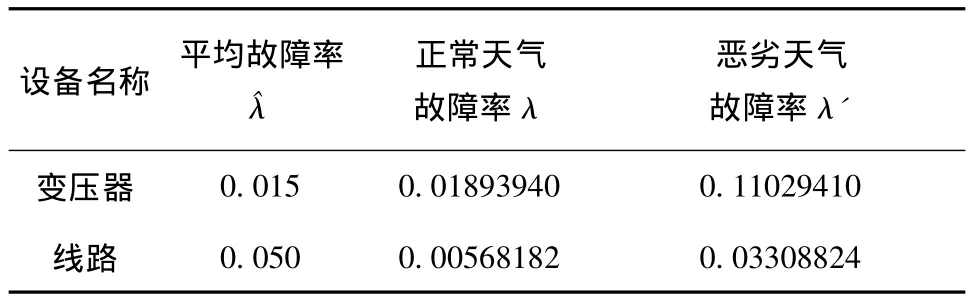
表2 修正后的元件故障参数Tab.2 Modified element fault parameters

表3 部分负荷点可靠性指标Tab.3 Part of load point reliability index

表4 不同方案系统可靠性指标Tab.4 System reliability index of different schemes
由表3、表4可以看到:
1)将方案1和方案2比较,考虑了断路器和熔断器拒动后,负荷点及系统的可靠性指标都有了明显变化,但计及断路器和熔断器拒动的概率,能更加真实地反应配电网可靠性的实际情况。
2)将方案1与方案3相比,考虑了气候条件,负荷点的停电率和停电时间都有了明显升高,系统的年停电次数和停电时间都有一定程度的增加,而可用度却降低了。因此,在考虑气候因素下,对配电系统进行可靠性评估更加准确。
5.2.2 风电场接入位置的配电网可靠性评估方案分析
方案4:考虑气候因素对元件故障率的影响,分别在区域1、区域2和区域3接入容量为1 MW的风力发电机,风电场仅满足区域内供电,接入馈线点分别是24、16、26,分析风电场不同接点接入对配电网可靠性的影响。
方案5:考虑气候因素对元件故障率的影响,同时在区域1、区域2和区域3接入容量为1 MW的风力发电机,风电场仅满足区域内供电,接入馈线点分别是24、16、26,分析多风电场接入对配电网可靠性的影响。
部分负荷点可靠性指标如表5所示,系统可靠性指标如表6所示。
由表5、表6可以看到:
1)将方案4结果与方案3结果比较,接入风机后系统的年停运率和停电时间指标都有了明显降低,系统的可用率有一定程度的优化提升,说明接入适量的风机对提升系统的可靠性是十分可行的。从负荷点指标对比来看,在风机区域范围内的负荷点,可靠性指标都有了一定程度优化,负荷停电频率有所升高,但平均停电时间和全年停电时间都明显下降,这是因为区域内负荷受到风机的故障率影响。而对于区域外的负荷点,可靠性指标无变化。方案4中不同点接入风电场,系统的可靠性变化也不一致,说明风电场的接入位置对系统的可靠性提升有很大的影响。
2)将方案5结果与方案4相比较,多地区接入风电场,负荷和系统的可靠性指标都有了更好的优化,说明在配电系统中接入适当容量的风电场,对系统的可靠性提升更加明显。
5.2.3 风电场孤岛划分对配电网可靠性评估方案的影响分析
方案7:区域3馈线点25接入2 MW风电场并网运行,发生故障时并网线重合闸停用。根据风电场出力满足其等值负荷最大为原则,带部分本地负荷形成孤岛运行,孤岛内负荷为 LP7、LP8、LP9、LP10、LP11、LP12、LP19、LP20、LP21、LP22、LP23。

表5 部分负荷点可靠性指标Tab.5 Part of load point reliability index

表6 不同方案系统可靠性指标Tab.6 System reliability index of different schemes

表7 不同方案系统可靠性指标Tab.7 System reliability index of different schemes
方案8:在区域3馈线点25接入2 MW风电场并网运行,故障时解列形成孤岛,孤岛外的负荷通过重合闸恢复供电。根据事先确定的解列点,将馈线25处的断路器F7断开形成孤岛,孤岛内负荷为LP19、LP20、LP21、LP22、LP23。
方案9:在区域3馈线点25接入2 MW风电场并网运行,故障时解列形成孤岛,孤岛外的负荷通过重合闸恢复供电。根据事先确定的解列点,将馈线10处的断路器F8断开形成孤岛,因为孤岛内负荷超过风电场装机容量,所以减去负荷LP13,维持孤岛稳定运行,孤岛内负荷为 LP8、LP9、LP10、LP11、LP12、LP19、LP20、LP21、LP22、LP23。
不同方案系统可靠性指标如表7所示。
由表7可以看到:
1)方案7与方案1相比,系统的可靠性指标都有明显变差,这是因为并网线停用重合闸,使孤岛外的负荷经历持续停电,降低了系统的可靠性,由此可见,风电场并网不一定能提高系统的可靠性。
2)方案8和方案9因线路瞬时性故障和永久性故障时,通过断开解列开关形成孤岛运行,孤岛外的负荷通过重合闸恢复供电,提高了系统的供电可靠性。比较方案8和方案9,发现解列点不同时系统的可靠性指标也不同,从系统可靠性方面来说方案9比方案8好。因此为了使系统的可靠性达到最优,需要预先规划好解列点,预先完善系统的自动控制措施和运行方式。
6 结论
1)为了使仿真结果更加真实地反应配电系统实际情况,分析了气候因素、开关元件拒动对配电系统可靠性分析的影响。
2)针对风电场接入对配电系统的影响,分析了风机不同节点、不同数量接入对可靠性的影响,并得出在配电系统中接入适量的风电场能够改善配电可靠性。
3)风电场接入系统并网运行时,合理计划孤岛划分,能更好地提高系统可靠性。
[1] 丁磊,潘贞存,王宾.分散电源并网对供电可靠性的影响分析[J].电力系统自动化,2007,31(20):89 93.DING Lei,PAN Zhencun,WANG Bin.Impact on reliability of distribution network with dispersed generators[J].Automation of Electric Power Systems,2007,31(20):89 93.
[2] 刘传铨,张焰.计及分布式电源的配电网供电可靠性[J].电力系统自动化,2007,31(22):46 49.LIU Chuanquan,ZHANG Yan.Distribution network reliability considering distribution generation[J].Automation of Electric Power Systems,2007,31(20):46 49.
[3] CASTRO R M G,FERREIRA L A F M.A comparison between chronological and probabilistic methods to estimate wind power capacity credit[J].IEEE Transactions on Power Systems,2001,16(4):904 909.
[4] 栗文义,张保会,巴根.风/柴/储能系统发电容量充裕度评估[J].中国电机工程学报,2006(16):62 67.LI Wenyi,ZHANG Baohui,BA Gen.Capacity adequacy evaluation of wind-diesel-storage system [J].Proceedings of CSEE,2006(16):62 67.
[5] 吴义纯,丁明,李生虎.风电场对发输电系统可靠性影响的评估[J].电工技术学报,2004(11):72 76.WU Yichun,DING Ming,LI Shenghu.Reliability assessment of wind farms in generation and transmission system[J].Transactions of China Electrotechnical Society,2004(11):72 76.
[6] 殷豪,肖文成,杨飞.含多风电场的地区电网供电可靠性研究[J].可再生能源,2013,31(9):39 43.YIN Hao,XIAO Wencheng,YANG Fei.Research on power supply reliability of regional power network with multiple wind farms[J].Renewable Energy,2013,31(9):39 43.
[7] 孙若笛.计及风速与负荷时序相关性的配电网可靠性评估[D].重庆:重庆大学,2012.SUN Ruodi.Reliability evaluation of distribution networks using Monte Carlo method considering correlations between wind speed and load[D].Chongqing:Chongqing University,2012.
[8] 齐雪雯.风速分布预测的指数平滑模型及其在配电网可靠性中的应用[D].重庆:重庆大学,2012.QI Xuewen.Exponential smoothing model for wind speed distribution forecast and its application in electrical distribution network[D].Chongqing:Chongqing University,2012.
[9] 孟安波,陈育成.基于虚拟预测与小波包变换的风电功率组合预测[J].电力系统保护与控制,2014,42(3):71 76.MENG Anbo,CHEN Yucheng.Wind power combination forecasting based on wavelet packet transform and virtual forecasting[J].Power System Protection and Control,2014,42(3):71 76.
[10] 丁明,吴义纯,张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报,2005(10).DING Ming,WU Yichun,ZHANG Lijun.Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms[J].Proceedings of CSEE,2005(10).
[11] 郭永基.电力系统可靠性分析[M].北京:清华大学出版社,2003.GUO Yongji.Reliability analysis of power system[M].Beijing:Tsinghua University Press,2003.
[12] 陈永进,任震,黄雯莹.考虑天气变化的可靠性评估模型与分析[J].电力系统自动化,2004,28(21):17 21.CHEN Yongjin,REN Zhen,HUANG Wenying.Model and analysis of power system reliability evaluation considering weather change[J].Automation of Power Systems,2004,28(21):17 21.
[13] KAIGUI X,JIAQI Z,BILLINTON R.Reliability evaluation algorithm for complex medium voltage electrical distribution networks based on the shortest path[J].IEE Proceedings of Generation,Transmission and Distribution,2003,150(6):686 690.
[14] BILLINTON R,JONNAVITHULA S.A test system for teaching overall power system reliability assessment[J].IEEE Transactions on Power Systems,1996,11(4):1670 1676.

