三角形空翼缘梁的极限承载力试验研究

魏建军，宋生志

（江苏建筑职业技术学院 建筑安全与减灾省级工程中心，江苏 徐州， 221116）

三角形空翼缘梁的极限承载力试验研究

魏建军，宋生志

（江苏建筑职业技术学院 建筑安全与减灾省级工程中心，江苏 徐州， 221116）

在澳大利亚学者提出的空翼缘梁（HFB）的基础上，提出一种新型三角形空翼缘梁（THFB）。通过试验测试，对三角形空翼缘梁（THFB）和传统H型钢梁在承受集中荷载作用下的破坏过程进行了对比，发现两种梁的破坏模态存在明显差异，THFB在集中荷载作用下极易发生局部屈曲，传统H型钢梁则易发生整体失稳，且THFB比传统H型钢梁具有较好的抗弯扭性能。利用有限元软件ANSYS对试验试件进行有限元模拟，试验结果和有限元模拟结果吻合较好。基于所建的有限元模型对THFB进行参数分析，参数主要包括上翼缘板厚、上翼缘板宽、腹板厚和钢材屈服强度，得出了THFB梁的承载力随不同参数的变化规律。最后结合理论和有限元分析，验证了Eurocode 3提供的H型钢梁设计公式计算THFB极限承载力的适用性。研究结果表明：采用Eurocode 3提供的H型钢梁设计公式对THFB的极限承载力进行验算是安全的，但偏于保守。

三角形空翼缘梁；承载力；试验；有限元分析

随着冷弯薄壁型钢在建筑业越来越广泛的应用，各国学者纷纷把寻求一种新型、安全、高效、经济的截面形式作为研究重点。早在20世纪90年代，澳大利亚学者 Dempsey［1－2］提出了空翼缘梁（HFB）。空翼缘梁的翼缘为两边支撑，较传统H型钢梁翼缘的一边支撑一边自由相比可以采用更薄的钢板，具有更大的宽厚比。试验研究了其在外力作用下发生畸变屈曲的模式，并提出了HFB作为梁和柱的设计方法。Pi等［3］基于模型试验及有限元法分析了HFB的弹性侧向畸变屈曲，认为扭转刚度的削弱是HFB发生畸变屈曲的主要原因。Heldt等［4］基于门式钢架分析了HFB发生侧向畸变屈曲的情况，得出增强HFB受拉翼缘约束能有效的提高梁的临界弯矩。Madendran等［5］对不同参数的9个 HFB试件进行了试验研究，提出了HFB理想夹支的试验方法。Avery等［6］采用有限元方法分析了HFB的受弯极限承载力，给出了材料非线性、局部屈曲、整体弯扭屈曲、腹板畸变屈曲、残余应力和几何缺陷等因素对梁临界弯矩的影响，并提出计算HFB极限抗弯承载力的简化多曲线设计法。徐金锋［7］提出两种新形式空翼缘梁—矩形空翼缘梁（RHFB）和五边形空翼缘梁（QHFB），研究了在纯弯状态下这两种梁的稳定承载性能，发现QHFB的屈曲模式同于HFB，但其抗扭刚度是 HFB的3～4倍。刘任峰［8－9］对矩形钢管空翼缘梁（RHFB）进行非线性分析，得出了梁跨及截面高度对梁承载力的影响。唐建民［10］对RHFB梁填充混凝土后的静力性能进行了研究，给出了影响其力学性能的参数变化规律。

基于上述研究发现，薄壁空翼缘梁较传统工字钢与H型钢梁具有截面开展、抗扭与抗弯刚度大等优点，可使得梁平面外稳定性能得到较大提高。目前中国对此类HFB的研究成果较少。本文开展了翼缘为空心封闭三角形截面的HFB的试验研究。它由一块薄壁钢板冷弯成闭合三角形截面作为受压翼缘，受拉翼缘仍采用条形钢板，整个截面呈单轴对称，此处称该梁为三角形空翼缘梁（THFB），见图1。本文结合试验测试和数值分析，研究了THFB在集中荷载作用下的非线性屈曲，并通过参数分析获得了不同几何参数和材料参数对梁承载力及破坏模态的影响规律。

1 试验方法

1.1 试件制作

试验设计THFB截面几何尺寸见图1，试验中设计1个H型钢梁做对比。两种梁的梁高、翼缘宽度、厚度及腹板厚度均相同，跨度为2 m。

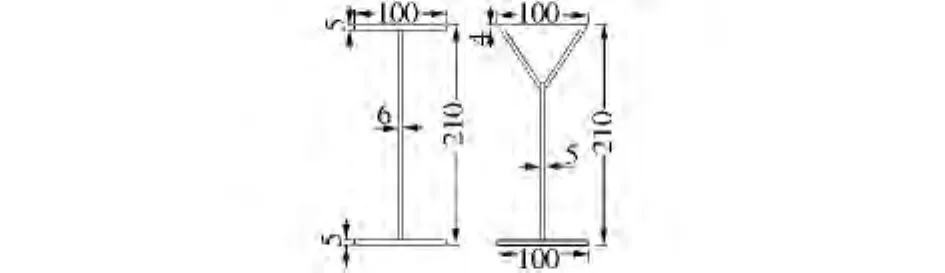
图1 试件梁的截面尺寸

1.2 试验装置及测试方案

所有试件均采用同一个加载装置。试验加载采用YES-5000型四柱压力试验机，如图2所示。试验设计为简支梁的单调加载试验，加载点位于跨中，支座处设有夹具，试件两端均被放置在夹具中，用来模拟理想“夹支”的约束条件，并提供侧向支撑。

图2 试验加载与夹支装置

试验采用分级加载制，每级加载10 k N，各级加载速度相同。每级加载完毕后采集跨中截面应变及位移。在梁跨中截面下翼缘处和腹板一侧安装位移计，监测跨中挠度及腹板侧向鼓曲变形。为保护上翼缘所贴应变片，加载点安放一个倒置槽钢，如图3所示。

图3 试件加载与位移计布置

依据《金属材料拉伸试验第一部分：室温试验方法》（GB／T 228.1－2010）对试件所用钢材进行了材性试验，所测数值见表1。

表1 钢材材料特性

2 试验结果

将试验测试得到的各构件的荷载值F为纵坐标，构件跨中的位移u为横坐标分别绘制荷载挠度曲线。同时，为方便分析，将有限元分析的结果绘制在图中。图5为H型钢梁的荷载挠度曲线，曲线中显示该构件的最大承载力Fu＝88.6 k N。从曲线可以看出，构件在破坏前经历了一定的塑性发展阶段，到达极值点后，构件先是上翼缘出平面外失稳，继而腹板随着向一侧屈曲，整个构件发生失稳。极值点过后，试验承载力急剧降低，其破坏模式为极值点失稳［11］。

利用有限元软件ANSYS建立分析模型，材料属性采用三折线弹塑性强化模型（即考虑了材料进入屈服后，由于钢材硬化对钢材强度提高的影响），其包括线弹性段、理想强化段和塑形流动段，满足Von Mises屈服准则。模型参数弹性模量、屈服强度和极限强度均通过对标准拉拔试件的试验测试得到，具体数值见表1。

由于焊缝、焊接残余应力、冷弯作用及初始缺陷等因素对梁承载力的影响非常小，因此在有限元模拟过程中，忽略了以上因素的影响。壳单元相对于实体单元能较准确模拟壳体的变形和内力情况，同时其还具有塑性、应力硬化、大变形以及大应变的特性，适用于分析薄壁和中等厚度壳体结构，模型分析中采用壳单元。有限元模型见图4，H型钢模型命名为T1，THFB模型命名为T2，分析中其边界约束条件及加载制度与试验保持一致。在模型中，限制梁体下翼缘两端平面内的竖向位移，且限制任意一端沿梁长度方向的水平位移，两端均可在平面内任意转动；限制梁两端沿平面外的水平位移，梁的两端施加“夹支”边界条件。在模拟计算过程中，均采用位移控制的加载方式，即通过集中力作用点处施加向下的位移来计算要施加的荷载。

图4 有限元模型

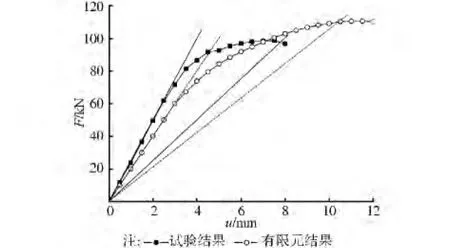
图5 H型钢梁荷载 挠度曲线

有限元分析得到荷载挠度曲线见图5，破坏模式见图6。

图6 H钢梁破坏模态

从图5可以看出，在弹性段及弹塑性段初期，采用有限元模拟的荷载 挠度曲线略低于试验测试的荷载 挠度曲线，这主要是因为H型钢梁试件两端采用夹支支座来模拟铰接约束条件，由于夹支支座会对试件端部的转动有一定的限制作用，而有限元模型两端采用理想铰接的约束条件，造成有限元模型模拟的刚度比试件的真实刚度稍微小些，因此数值计算得到的荷载 挠度曲线也就略低于试验测试的荷载 挠度曲线。当进入塑性强化阶段时，试件由于存在加工缺陷提前发生了失稳破坏，后期有限元计算结果高于试验测试结果。通过两倍弹性斜率准则［12］对试验测试及有限元计算的极限承载力进行判定，得到两者的极限承载力分别为：99.2、107.3 k N，两者相差约8.2%，在可接受的范围内。

从试件和有限元模型的破坏模态对比图中可以看出，有限元的破坏模式与试验现象非常相似，说明有限元计算能够较为准确地模拟构件的受力过程。

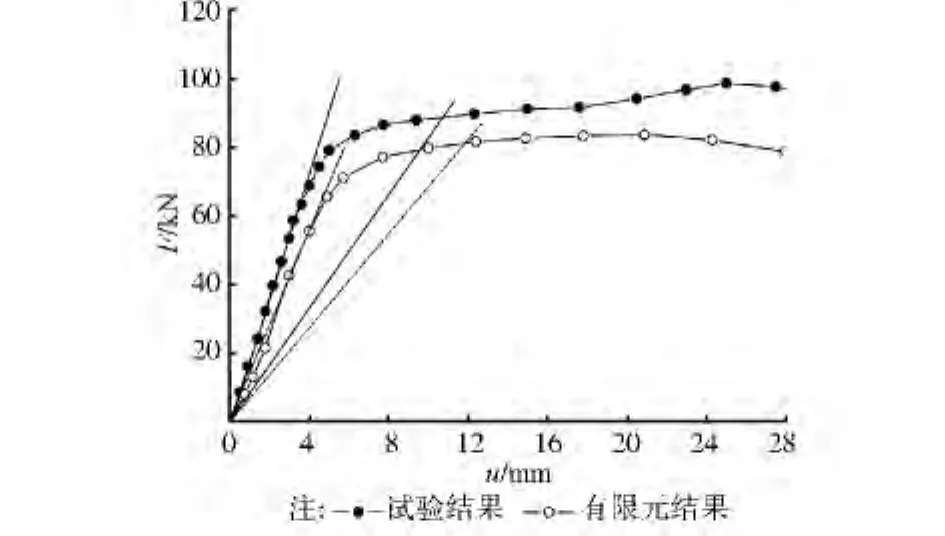
图7 THFB梁的荷载 挠度曲线

THFB试件的荷载挠度曲线见图7，采用两倍弹性斜率准则对其极限承载力进行判定，得到试验测试及有限元模拟的极限承载力分别为Fu＝88.6 k N和Fu＝81.2 k N，差别主要是由于试件两端夹支约束导致试件刚度变大所造成的，两者相差约为9.1%，在可接受的范围内。图5显示H型梁有限元模型计算结果在塑性强化阶段后期荷载逐渐升高，而THFB有限元模型并未出现此种现象，主要是由于THFB试件和模型均发了塑性强度破坏，并未与H型梁相似出现梁的整体失稳破坏。THFB试件的破坏模式图如图8所示。上翼缘板呈现局部屈曲破坏的特征，屈曲仅局限在靠近加载位置的一小部分区域。随着荷载的增加，挠度持续增加，梁体在破坏前经历了较长的塑形发展阶段后失稳破坏。极值过后，承载力下降，但保持有一定的屈曲后承载力。构件的屈强比约为86。有限元分析与试验结果非常接近，可以认为所采用的有限元模型能够作为试验分析的补充手段，也可以用来进行更深入的参数分析。

图8 THFB梁破坏模态

3 THFB参数分析

由于影响钢梁承载力的因素较多，为了更深入了解影响THFB承载力的影响因素，以有限元模型T2为基础进行参数分析。上翼缘厚度t、上翼缘宽度B、腹板厚度tf和钢材屈服强度fy等参数成为本次分析的对象，如图9所示。所有参数对THFB梁承载力的影响均基于相对极限承载力进行比较，为数值计算所得承载力与梁截面面积的比值。

图9 THFB的截面参数

3.1 上翼缘板厚t的变化

选取梁高H为210 mm，翼缘宽度B为100 mm、腹板厚tf为2 mm和屈服强度fy为345 MP的THFB梁作为基本模型进行分析，计算模型的参数如表2所示。模型分组命名规则为A-n-L，此处A为模型组别，n为主变化参数序号，L为跨度序号。

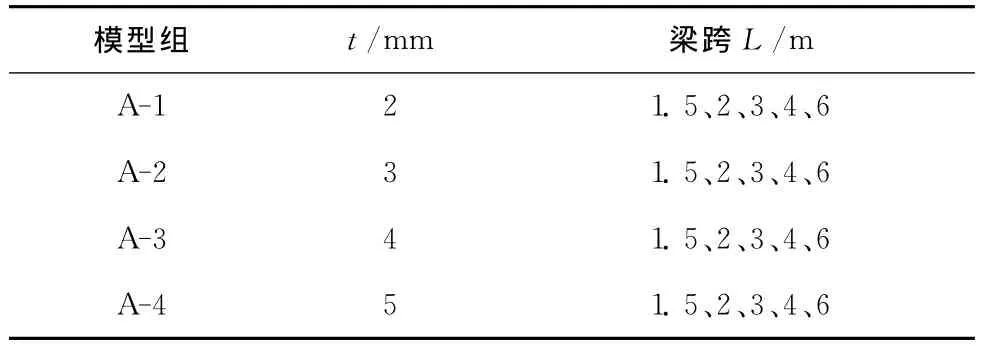
表2 模型A参数取值

图10 上翼缘板厚变化对THFB承载力影响

3.2 上翼缘板宽度B的变化

选取H为300 mm、fy为345 MP、t和tf均为4 mm的THFB梁作为基本模型进行分析，计算模型的参数如表3所示。

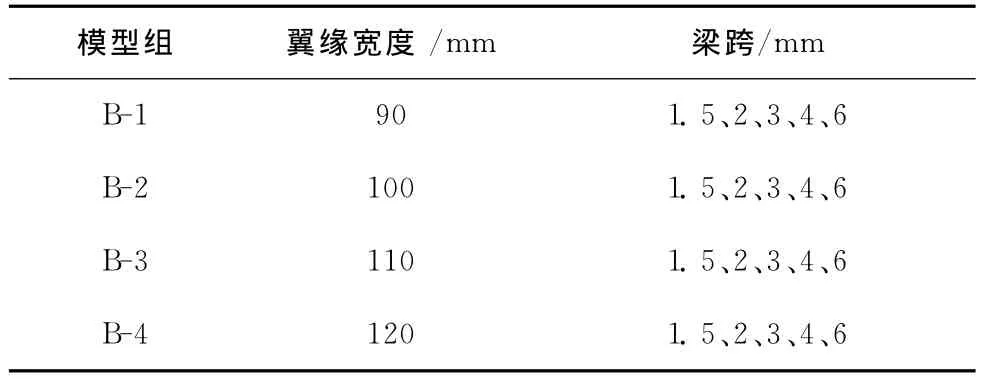
表3 模型B参数取值

分析图11可以得到，对于跨度小于4 m的THFB梁，其相对极限承载力随翼缘宽度的增大而降低；当梁跨大于4 m后，上翼缘宽度的变化对其相对极限承载力影响较小。

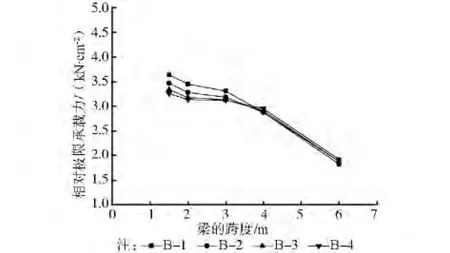
图11 上翼缘宽度变化对THFB承载力影响

3.3 腹板厚t f的变化

选取H为300 mm、t为4 mm、B为100 mm和fy为345 MPa的THFB梁作为基本模型进行分析，计算模型的参数如表4所示。

表4 模型C参数取值

分析图12可以得到，对于梁跨L小于4 m的THFB，增加腹板厚度对梁承载力提高显著。但对腹板厚度tf大于5 mm、梁跨L大于4 m的THFB，改变tf对极限承载力几乎没有影响，原因是由于腹板的刚度随厚度增加而变大，梁的破坏由腹板屈曲转变为翼缘屈曲。建议梁跨小于4 m的THFB可以通过增大腹板厚度的方式来提高其极限承载力；但对梁跨大于4 m的THFB，其腹板设计厚度不宜大于4 mm。

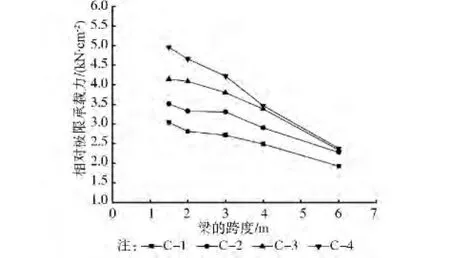
图12 腹板厚变化对THFB承载力影响

3.4 屈服强度f y变化

选取H 为210 mm、B为100 mm、t和tf均为4 mm的THFB梁作为基本模型进行分析，计算模型的参数如表5所示。

表5 模型D参数取值

由图13可以发现，THFB梁的相对极限承载力随钢材屈服强度的增加而增大，说明THFB梁达到极限承载力时均发生了一定的塑性变形。但其屈服强度大于345 MPa后，相对极限承载力增幅减小明显，表明采用Q345钢材制作THFB梁较为经济。

图13 屈服强度变化对THFB承载力

4 THFB极限承载力评价

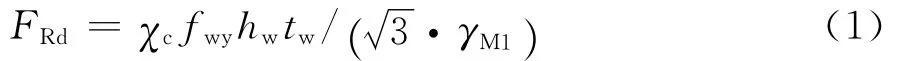
式中：FRd为腹板的抗剪承载力设计值；fwy为腹板材料屈服强度；γM1为抗力分项系数；χc为考虑屈曲的承载力折减系数，对局部屈曲和整体屈曲分别为χc，1和χc，g，不考虑梁的非弹性屈曲，承载力折减系数可以由下式得到。

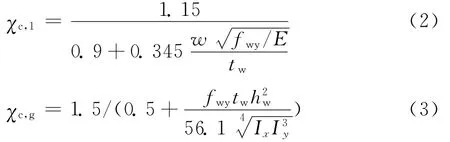
现行规范中尚没有对空心翼缘梁承载力计算的规定。文献［3］和［6］中提到HFB在不设置横向加劲肋情况下极易发生畸变屈曲及腹板屈曲。本试验中，T1构件发生整体弯扭屈曲，试件T2发生翼缘压屈，有限元试验模型A～D中还有腹板屈曲和畸变屈曲等破坏模式。中国规范［13］用限制翼缘宽厚比和设置加劲肋方式保证局部稳定；欧洲规范Eurocode 3［14］给出了一般不设加劲肋H型钢局部屈曲和整体屈曲统一的承载力设计值表达式。本文拟验证Eurocode 3提供的H型钢梁的计算公式对THFB承载力计算的适用性。对THFB试验模拟将建立200个模型进行数据拟合，其成果另文发表。欧洲规范Eurocode 3给出的不设加劲肋的H型钢承载力设计值计算统一公式：

将各个试件的计算结果进行列表比较，见表6。表中Fform和Ffem分别为按照式（1）和有限元计算得到的承载力，Fe为试验荷载。

表7 试件承载力比较

经过对比发现，基于H型钢的承载力设计公式应用于HFB设计时，计算出来的承载力偏于保守。试件T2有限元计算结果介于公式计算值和试验值之间，说明模型计算较为可靠有效，但T2试件设计翼缘过薄，试验加载中出现翼缘屈曲，有研究文献证实将翼缘进行增加厚度或填充混凝土加强后，HFB将有更优的承载性能［15－16］。其他试件公式计算值均小于有限元结果，说明采用H型钢设计公式可以验算THFB的极限承载力。

5 结 论

基于对三角形空翼缘梁和H型钢梁的试验测试和有限元分析，可以得到以下结论：

1）与传统H型钢梁相比，THFB梁上空心翼缘难以承受荷载的局部压力，极易发生翼缘板的局部屈曲，需要在设计时通过设置加劲肋或局部填充来改良。

2）可以采用Eurocode 3提供的H型钢梁设计公式进行THFB的极限承载力验算。

3）跨径对THFB的极限承载力影响显著，在研究该梁的设计理论时，必须分为跨径小于4 m和大于4 m两类分开研究。

［1］Dempsey R I.Advantages of the hollow flange beam in structural applications ［C ］／／National Conference Publication-Institution of Engineers，Australia，1991：1-9.

［2］Dempsey R I.Structural behavior and design of hollow flange beams ［C］／／National Conference Publication-Institution of Engineers，Australia，1990：327-335.

［3］Pi Y L，Trahair N S.Lateral-distortional buckling of hollow flange beams ［J］.Journal of the Structure Engineering，1997，123（6）：695-702.

［4］Heldt T J，Mahendran M.The buckling behavior of hollow flange beams in portal frame buildings ［J］.Structural Steel 4PSSC，Singapore，95：173-180

［5］Mahendran M，Doan V.Lateral distortional buckling tests of hollow flange beams.Research monograph99-3［S］.Physical Infrastructure Centre，QUT，Brisbane，Australia，1999.

［6］Avery P，Mahendran M，Nasir A.Flexural capacity of hollow flange beams［J］.Journal of Constructional Steel Research，2000，53：201-223.

［7］徐金锋.新型空翼缘梁的稳定承载力性能研究［D］.哈尔滨：哈尔滨工业大学，2005：1-57

［8］刘任峰.上翼缘为矩形管的新型工字形梁静力性能分析［D］.哈尔滨：哈尔滨工业大学，2006：1-90.

［9］刘任峰，武振宇.腹板加劲肋对空翼缘梁LHFB承载能力的影响［J］.哈尔滨工业大学学报，2008，40（6）：855-859.

Liu R F，Wu Z Y.Effect of web stiffeners on the loadcarrying capacity of hollow flange beam LHFB ［J］.Journal of Harbin Institute of Technology，2008，40（6）：855-859.

［10］唐建民.矩形钢管混凝土上翼缘梁静力性能参数分析［J］.山东理工大学学报：自然科学版，2011，25（4）：41-45.

Tang J M.Parameter analysis on static behavior of rectangular concrete-filled steel tube top flange beams［J］.Journal of Shandong University of Technology：Natural Science Edition，2011，25（4）：41-45.

［11］陈绍藩.钢结构设计原理［M］.北京：科学出版社，2005.

［12］GB 50017－2003钢结构设计规范［S］.北京：中国计划出版社，2003.

［13］EN 1993-1-8 Eurocode 3：design of steel structure Part 1-5： Plated structural elements ［S］.Brussels：European Committee for Standardization，2005

［14］Bambach M R.Design of hollow and concrete filled steel and stainless steel tubular columns for transverse impact loads ［J］.Thin-Walled Structures，2011，49：1251-1260

［15］武振宇，成博，何嘉.矩形钢管混凝土上翼缘梁静力性能分析［J］.低温建筑技术，2009，135（9）：39-42.

Wu Z Y，Cheng B，He J.Experimental reasearch on static behavior of I-beam with a rectangular concretefilled tube top flange ［J］. Low Temperature Architecture Technology，2009，135（9）：39-42.

（编辑 王秀玲）

Experimental Analysis of Bearing Capacity of Triangle Hollow Flange Beam

Wei Jianjun，Song Shengzhi

（Construction Safety and Disaster Mitigation Engineering Research Center，Jiangsu Institute of Architectural Technology，Xuzhou 221116，Jiangsu，China）

On the basis of Hollow Flange Beam （HFB）which is proposed by Australian researchers，a new pattern triangle hollow flange beam （THFB）is presented.According to the experimental test and finite element simulation，the failure processes of THFB and traditional I-beam under concentrated load are compared，and then the obvious differences between the failure modes of these two type beams are founded.The local buckling is easily occurred for the THFB，while overall instability is easily occurred for traditional I-beam，and THFB possesses have better bending performance and twist resistance than those of traditional I-beam.with the experiments，finite element analysis is carried out by FE software ANSYS，and the FE results agree with the test results.Based on FE models，the parameter analysis is carried out for THFB.The parameters mainly include the thickness of top flange，the width of top flange，the thickness of web and the yield strength of steel.The change rule of the bearing capacity of THFB with different parameters can be achieved by parameter analysis.Finally，based on the above results，the applicability of the calculation formula of Eurocode3 to compute the bearing capacity of THFB is discussed.The results show that it is safe and reliable to adopt the calculation formula of Eurocode3 to compute the bearing capacity of THFB，Whilst the estimation is relatively conservative.

triangle hollow flange beam （THFB）；concentrated load；experimental test；finite element stimulation.

TU391

A

1674-4764（2014）02-0106-06

10.11835／j.issn.1674-4764.2014.03.017

2013-09-15

住房与城乡建设部科学技术计划项目（2011-k8-12）；江苏省教育厅高校科研成果产业化推进项目（JHB2011-66、JHB2012-69）；江苏省高校青蓝工程资助

魏建军（1974-），男，副教授，博士，主要从事结构与岩土工程共同作用、组合结构抗冲击研究，（E-mail）jzaqlab＠163.com。