两相邻建筑“结构-土-结构体系”的动力特性

潘旦光，豆丽萍，2

（1.北京科技大学 土木与环境工程学院，北京 100083；2.银川世茂房地产开发有限公司，银川 750002）

两相邻建筑“结构-土-结构体系”的动力特性

潘旦光1，豆丽萍1，2

（1.北京科技大学 土木与环境工程学院，北京 100083；2.银川世茂房地产开发有限公司，银川 750002）

为了研究建筑群中相邻结构存在导致结构动力特性的变化，将上部结构简化为等效单自由度模型，采用刚性基础明置于均质土层上，系统地研究两个相同结构所构成三维结构-土-结构体系中，邻近结构存在对结构动力特性的影响。根据结构-土-结构相互作用下体系存在两阶频率相近相位相反振动模态的现象，提出了孪生频率的概念。随后，探讨了孪生频率随结构与土层的频率比、结构之间的相对距离、基础宽度与土层厚度比等因素的变化规律，以反映两结构通过土体耦合对结构动力特性的影响。在此基础上，进行了行波地震输入下结构-土-结构相互作用体系动力反应计算，结果表明，由于孪生频率的存在，易于使结构和场地产生拍的现象。

结构-土-结构相互作用；动力特性；相对距离；频率比；拍

为了充分地利用土地，建筑与建筑之间的间距往往很小。日本的Kobe、法国的Nice、美国的Los Angeles、中国的上海等城市部分或全部修建在软土场地上，且位于地震带上或地震带的边缘。在地震作用下，土与结构之间的相互作用（soil-structure interaction，简称SSI）是影响结构动力反应的关键因素之一［1－3］。局部区域内的建筑必将通过地基土对相邻结构的动力反应产生影响［4－5］，由此存在结构-土-结构相互作用（structure-soil-structure interaction，简称SSSI）问题。

Luco等［6］首先研究了SH波作用下SSSI问题。Wolf［7］对反应堆建筑、反应堆辅助室和燃料处理室组合结构进行地震反应分析。田彼得等［8］采用二维边界元法研究弹性半空上两个条形结构的动力阻抗和动力反应。姜忻良等［9］研究两结构的动力反应随相互之间距离的变化规律。窦立军［10］分析了高层建筑对相邻多层建筑的影响。Padron等［11］研究了桩基结构的SSSI。Clouteau等［12］的计算结果表明，与SSI体系相比SSSI体系可使结构顶层的反应降低。王淮峰等［13］研究了由于相邻结构存在情况下基地剪力的变化情况。

在一定区域范围内的结构通过土体耦合而成为一个有机的整体。结构之间距离和结构基础宽度等的变化相当于改变了系统的质量和刚度分布，由此导致结构动力特性发生相应的变化。而结构的动力特性是影响结构的动力反应最关键的因素之一。为此，本文将上部结构简化为等效单自由度体系，比较两相同结构组成的结构-土-结构相互作用体系与单一结构下土 结构相互作用体系动力特性的变化情况，系统地研究结构-土-结构体系动力特性随结构间的相对距离、结构与土体相对刚度比和基础宽度的变化规律。

1 体系的计算模型

上部结构简化为等效单自由度体系，基础采用明置于等厚度均质水平土层上的方形刚性基础，所构成的结构-土-结构相互作用体系如图1所示。

图中B、L、H、D分别表示基础宽度、两基础间净距、土层厚度以及基础边界距人工边界的距离。将土体和结构进行有限元划分后，体系的无阻尼自由振动方程可表示为：

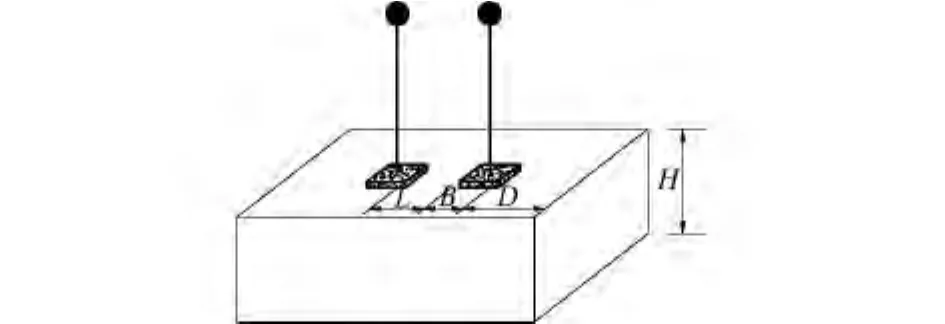
图1 结构-土-结构相互作用计算简图

土层实际为一半无限体，当采取用有限元法进行计算时，需要截取一定的范围进行计算，由此带来人工边界的问题［14－15］。下面基于SSI体系的有限元模型讨论侧向人工边界范围的选取问题。计算中侧向人工边界为自由边界，底部采用固定边界。SSI体系基频随D／B变化的计算结果如表1所示。从计算结果可以看出，当D／B大于8后，结构基频的计算数值趋于稳定。因此，下面计算中侧向人工边界范围取为D／B＝8，以消除侧向人工边界对结构基频的影响。计算中土体的参数如下：弹性模量为2.0×107Pa，泊松比为0.3，密度为1 600 kg／m3，厚度为8 m。刚性基础宽度为8 m，忽略基础的质量。上部结构在刚性基础下的频率为13.63 rad／s。此时，结构和土层的频率比＝1，基础宽度与土层厚度比＝1。

表1 不同D／B下SSI体系的基频

从上部结构的计算模型看，刚性基础上的质量弹簧系统可以看作是采用筏基的建筑结构。设筏基的质量为mf，上部结构的质量为m。则不同mf／m下结构的基频如表2所示。表中的误差为采用无质量刚性基础近似计算所得频率的相对误差。显然随着基础质量的增加，采用无质量刚性基础SSI体系计算频率的误差将增加。实际工程中，筏基结构的mf／m一般为5%，此时，采用无质量基础的计算误差小于0.5%。因此，为简化计算参数，在后面的计算分析中将基础简化为无质量的刚性基础。

表2 不同m f／m下SSI体系的基频

图2为不同距离下结构-土-结构相互作用体系自振频率和相应-土-结构相互作用体系自振频率的计算结果。从计算结果可以看出，考虑土 结构相互作用后，结构体系的频率小于刚性基础下结构的频率，这一点与其它相关文献的理论和试验结果相同［16］。但是，对于单自由度下单一结构的土 结构相互作用体系而言，结构任一方向水平振动的主模态只有一阶，而与之对应的结构-土-结构相互作用体系的模态将是两阶频率相近的模态。其中一阶模态为两个结构同向运动，另一阶模态为两个结构相向运动，如图3所示。

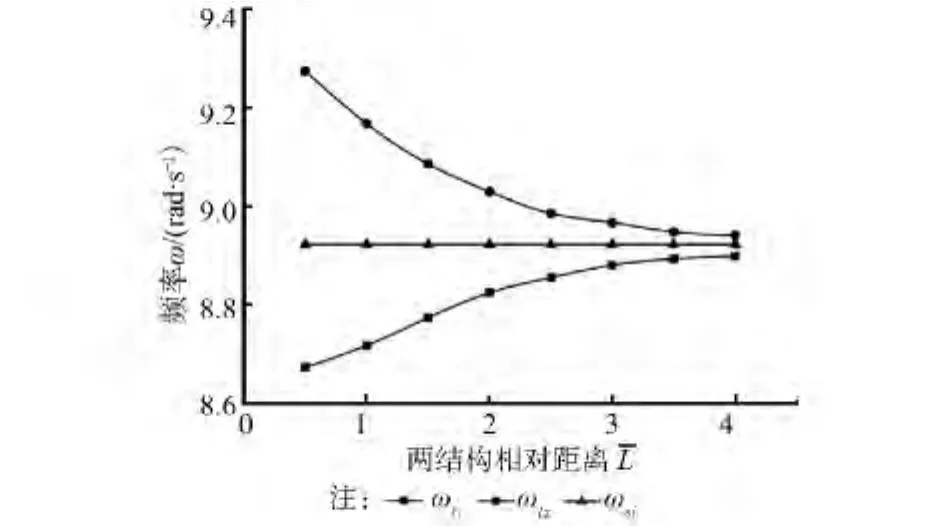
图2 SSSI体系频率随两结构相对距离的变化

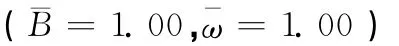
图3 SSSI系统模态

结构-土-结构体系中两阶频率相近模态是两个相邻结构通过土体耦合而产生的特殊的动力特征，具有对称性相反、频率相近的特点。为描述方便，将这样的两阶频率称为“孪生频率”。并定义孪生频率相对变化量为：

式中ωt2和ωt1分别为孪生频率的上限和下限，ωsi为与孪生频率对应的SSI体系的频率。

从图2可以看出：1）结构-土-结构体系的孪生频率分别位于相应土 结构相互作用体系频率的两侧；2）当两个结构相距越远，ωt2和ωt1逐渐收敛到ωsi，这表明随着两个结构彼此之间距离的增加，两结构通过土体的耦合效应逐渐减少，当两者之间的距离达到一定程度后，这种相互作用可以忽略不计。而综合反映了结构土结构相互作用体系相对于土 结构体系频率的变化情况，可作为描述结构之间相互影响的特征参数。

下面主要分析两相同结构所组成的结构-土-结构相互作用系统的频率变化情况。对结构体系频率的影响因素采用以下无量纲参数进行描述：结构和土层的频率比：＝ωst／ωso；两结构相对距离：＝L／B；宽厚比：＝B／H。其中，ωst表示刚性基础下结构的频率，ωso表示仅均质土层的基频。宽厚比是基础宽度与土层厚度比，间接反映上部结构的细长比。

2 土-结构相互作用体系的频率

结构-土-结构相互作用对结构动力特性的影响是在土 结构相互作用体系动力特性的基础上，由于邻近构筑物存在而发生的变化。为更好的理解孪生频率的变化规律，下面首先分析土 结构相互作用体系频率ωsi随频率比和宽厚比的变化情况。计算中土层参数同前，保持不变。图4为改变结构刚度和结构基础宽度情况下土 结构相互作用体系频率ωsi的变化规律。

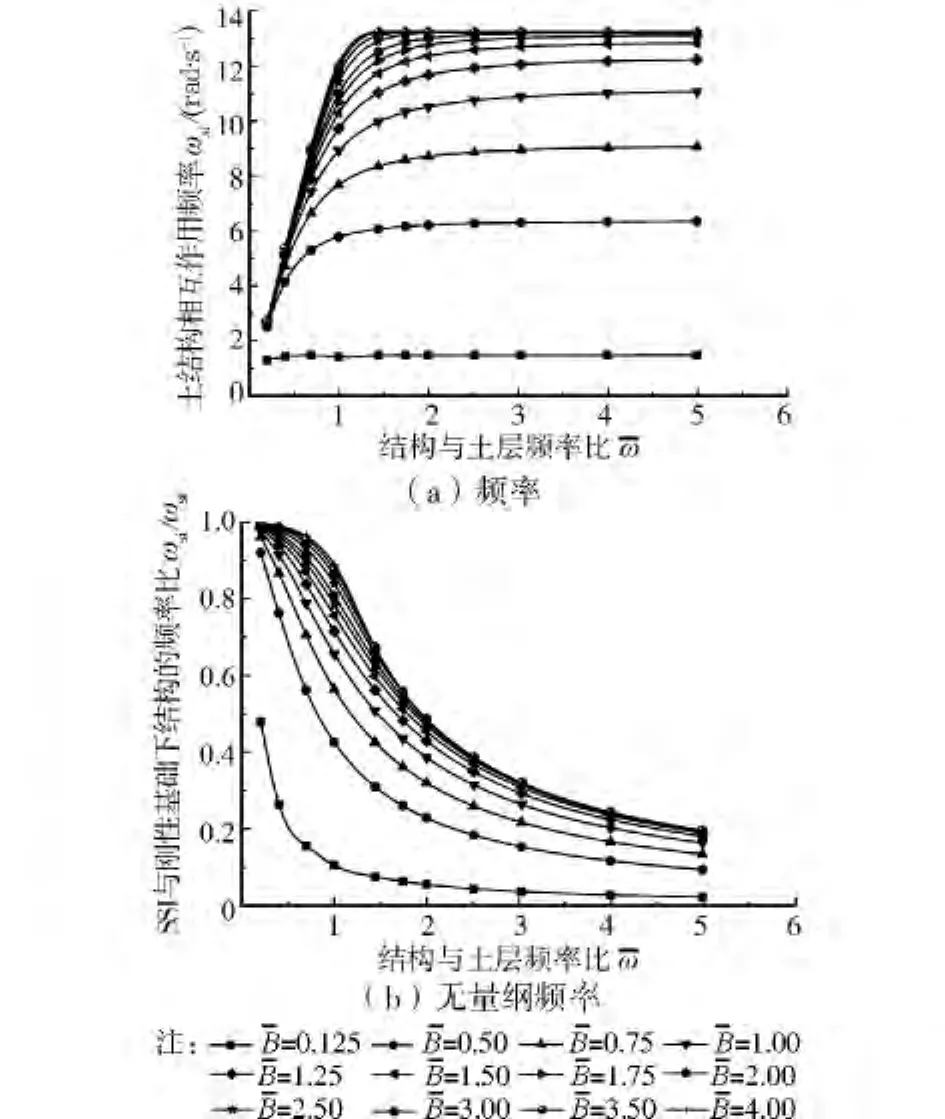
图4 土-结构相互作用体系的频率

因此，在下面分析结构-土-结构相互作用体系孪生频率相对变化量Δt时，频率比和宽厚比的计算范围分别取为［0.2，5］和［0.125，4］。

3 孪生频率相对变化量的影响因素

图5 随相对距离的变化

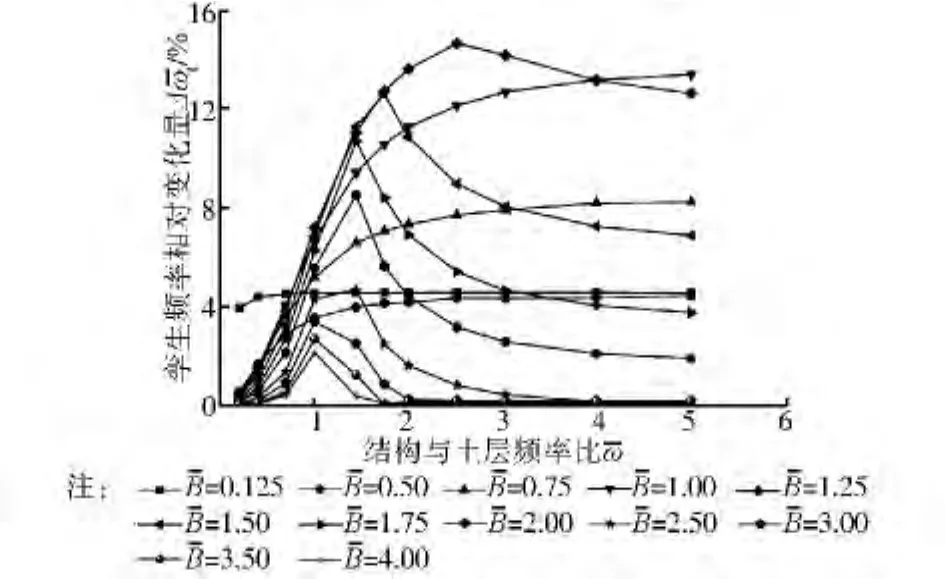
图6 随频率比的变化 （＝0.5）

图7 随基础宽度的变化（＝2.00）

4 行波地震输入下SSSI体系的反应

SSSI体系可作为分析城市环境下结构动力反应的基础。1985年墨西哥地震时，人们首先观察到城市条件下场地地震波中出现异常的长持时和拍的现象［17］，并基于结构-土-结构相互作用模型的地震反应分析再现了拍的情况。由前面的分析可知，结构-土-结构相互作用体系存在两阶频率相近但相位相反的模态，这表明建筑结构群下存在引起拍频振动的条件。为此下面以简谐荷载为例，说明结构 土结构体系在地震作用下拍的现象。

地震时从震源释放出来的能量以地震波的形式在场地内传播，因而不同点的地震动必然存在差异。在当前对基岩地震波的分布规律尚缺乏深入认识的情况下，文中采用行进地震波假定，即土层地震输入为行波输入［18］。在有限元模型中，如果入射起始点的地震波位移时程为ub0（t）时，那么在地震波传播方向上，与入射点相距xi处的水平方向位移时程可以表示为：

式中c为地震波的行进速度。

算例分析两相同单自由度体系明置于一均质土层的SSSI体系，如图8所示。同时，在有限元模型中仅保留结构1即形成SSI体系。有限元模型中的参数为：土的计算范围为296 m×80 m（长×宽），厚度为16 m，土的弹性模量为8.0×107Pa，泊松比为0.3，密度为1 600 kg／m3，刚性基础尺寸为16 m×16 m，两结构之间的距离为24 m。SSI体系的基频为1.66 Hz，SSSI体系与之相对应的孪生频率分别为1.64 Hz和1.68 Hz。

图8 结构-土-结构体系有限元模型

为定性研究行波输入情况下，SSSI体系和SSI体系结构动力反应的差别，假定输入地震波为从左向右传播的简谐波，振幅为1 cm，激振频率取略小于基频的1.44 Hz，以突出孪生频率对拍的影响。计算中简谐波的行进速度假定为200 m／s，激振时间为40 s。

图9 结构1位移响应

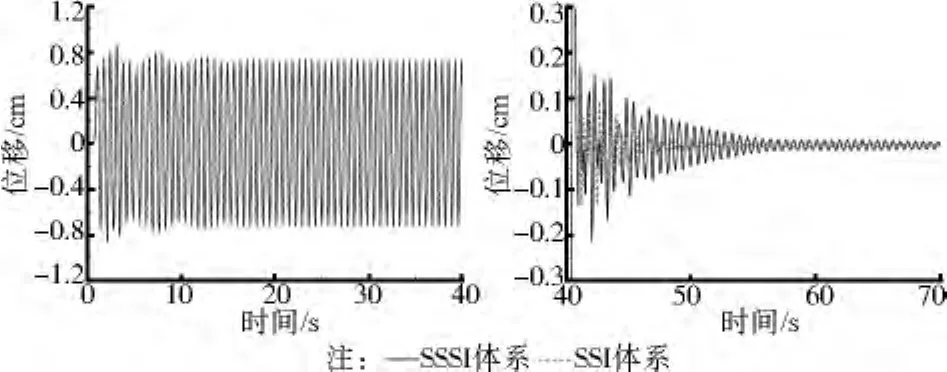
图10 地表A点位移响应

SSSI体系和SSI体系结构1的谐振反应如图9所示。图10为地表A点的位移反应时程。由图可知：1）对于该简谐荷载和行波波速下，相邻结构对振动初期的瞬态振动有较大影响，对稳态振动影响很小。2）在地震波通过场地后，SSSI体系自由振动的结构和场地都出现拍的现象，但是SSI体系没有拍的现象。与SSI体系的位移时程相比，相邻结构使土层表面自由振动衰减速度降低和持时延长。

在行波输入下，不同激振点输入地震波有时间差（相位差）的存在。地震波的行进速度与下覆土层的剪切波速和入射角度有关，为此比较了Δt／T分别等于0、1／8、1／4、1／2和1情况下，SSSI体系中结构1的动力反应的差别，如图11所示。图中Δt表示地震波通过相应于两结构水平投影位置的时间差，T表示简谐荷载的周期。计算中取T＝0.48 s，其余计算参数同前。Δt／T＝0表示行进波速为无穷大，即地震输入为一致输入。两相同结构所组成的SSSI体系中，孪生频率分别为反对称模态和正对称模态，在一致输入作用下无法激起正对称模态的振动，因此，不会因为孪生频率而产生拍，图11的动力反应也反映了这个现象。在行波输入下，可以同时激发正对称模态和反对称模态，因此，结构1自由振动阶段都出现了拍的现象。由此表明，当结构间距离导致不同结构物之间的输入地震波有明显相位差时，易于产生拍的现象。

图11 不同相位差下SSSI体系中结构1位移响应

5 结 语

采用有限元方法研究了相邻结构对结构-土-结构体系动力特性的影响。系统地讨论了SSSI体系结构动力特性随两结构之间相对距离、频率比以及结构基础宽度与土层厚度比的变化规律。根据计算结果可以得出以下结论：

1）根据两相同结构下结构-土-结构体系中存在两阶频率相近，相位相反的模态，提出了“孪生频率”的概念。在此基础上，进一步提出“孪生频率相对变化量”指标用以定量描述两相邻结构的动力相互作用。

2）两结构间的相对距离大于2.5倍基础宽度时，相邻结构对结构动力特性的影响小于5%，可以忽略两结构间的动力相互作用。

6）当结构间距离导致不同结构物之间的输入地震波有明显相位差时，结构-土-结构相互作用体系中存在孪生频率而使结构和邻近场地易于产生拍的现象。

［1］Paul S J.Design aids for simplified nonlinear soilstructure interaction analyses ［J］. Engineering Structures，2012，34：572-580.

［2］Farshidianfar A，Soheili S.Ant colony optimization of tuned mass dampers for earthquake oscillations of highrise structures including soil-structure interaction ［J］.Soil Dynamics and Earthquake Engineering，2013，51：14-22.

［3］Jarernprasert S，Bazan-Zurita E，Bielak J.Seismic soilstructure interaction response of inelastic structures［J］.Soil Dynamics and Earthquake Engineering，2013，47：132-143.

［4］Ghergu M，Ionescu I R. Structure-soil-structure coupling in seismic excitation and ‘city effect’［J］.International Journal of Engineering Science，2009，47（3）：342-354.

［5］Lou M， Wang H，Chen X，et al.Structure-soilstructure interaction：literature review ［J］.Soil Dynamics and Earthquake Engineering，2011，31（12）：1724-1731.

［6］Luco J E，Contesse L.Dynamic structure-soil-structure interaction［J］.Bulletin of the Seismological Society of America，1973，63（4）：1289-1303.

［7］Wolf J P.Dynamic soil-structure interaction ［M］.Englewood Cliffs，N.J.：Prentice-Hall，1985.

［8］田彼得，俞载道.结构-土-结构相互作用体系的动力分析［J］.同济大学学报：自然科学版，1987，15（2）：16-27.

Tian B D，Yu Z D.Dynamic analysis of structure-soilstructure interaction［J］.Journal of Tongji University：Natural Science，1987，15（2）：16-27.

［9］姜忻良，严宗达，武志金.相邻结构 地基 土相互作用的分支模态实用研究 ［J］.地震工程与工程振动，1998，18（3）：9-14.

Jiang X L，Yan Z D，Wu Z J.Research on practical method of branched mode for neighboring structures foundation soil interaction system ［J］.Journal of Earthquake Engineering and Engineering Vibration，1998，18（3）：8-13.

［10］窦立军，杨柏坡.高层建筑与相邻多层建筑间的动力相互作用［J］.地震工程与工程振动，2000，20（3）：15-21.

Dou L J，Yang B P.Dynamic interaction of tall building with neighboring multi-storied building［J］.Journal of Earthquake Engineering and Engineering Vibration，2000，20（3）：15-21.

［11］Padron L A， Aznarez J J， Maeso O.Dynamic structure-soil-structure interaction between nearby piled buildings under seismic excitation by BEM-FEM model［J］.Soil Dynamics and Earthquake Engineering，2009，29（6）：1084-1096.

［12］Clouteau D，Broc D，Devesa G，et al.Calculation methods of Structure-Soil-Structure Interaction （3SI）for embedded buildings：application to NUPEC tests［J］.Soil Dynamics and Earthquake Engineering，2012，32（1）129-142.

［13］王淮峰，楼梦麟，陈希，等.建筑群结构-土-结构相互作用的影响参数研究［J］.同济大学学报：自然科学版，2013，41（4）：510-514.

Wang H F，Lou M L，Chen X，et al.Parametric study on structure-soil-structure interaction of high-rise buildings［J］.Journal of Tongji University：Natural Science，2013，41（4）：510-514.

［14］潘旦光，楼梦麟，董聪.一致输入作用下土层的地震反应分析［J］.计算力学学报，2005，22（5）：562-567.

Pan D G，Lou M L，Dong C.Seismic response analysis of soil layer under uniform excitation［J］.Chinese Journal of Computational Mechanics，2005，22（5）：562-567.

［15］李煌.地基与高层建筑结构动力相互作用分析［D］.南宁：广西大学，2006.

［16］李辉，赖明，白绍良.土 结动力相互作用研究综述（Ⅰ）——研究的历史、现状与展望［J］.重庆建筑大学学报，1999，21（4）：112-116.

Li H，Lai M，Bai S L.A Summary of research on soilstructure dynamic interaction （I）－－history，status in quo and prospects［J］.Journal of Chongqing Jianzhu University，1999，21（4）：112-116.

［17］Groby J P，Wirgin A.Seismic motion in urban sites consisting of blocks in welded contact with a soft layer overlying a hard half-space ［J］.Geophysical Journal International，2008，172（2）：725-758.

［18］潘旦光，楼梦麟，董聪.土层地震行波反应分析中侧向人工边界的影响［J］.岩土工程学报，2005，27（3）：308-312.

Pan D G，Lou M L，Dong C.Effect of vertical artifical boundary on seismic response of soil layer under traveling wave excitations ［J］.Chinese Journal of Geotechnical Engineering，2005，27（3）：308-312.

（编辑 吕建斌）

Dynamic Characteristics of Structure-Soil-Structure System for Two Neighbor Buildings

Pan Danguang1，Dou Liping1，2

（1.School of Civil and Environmental Engineering，University of Science and Technology Beijing，Beijing 100083，P.R.China；2.Yinchuan ShiMao Real Estate Development Co.Ltd，Yinchuan 750002，P.R.China）

In order to realize the variation of structural dynamic characterics due to neighbor structures in buildings，the surface structure is idealized as an equivalent single degree of freedom system with rigid base whose site consists of a single homogeneous layer.The dynamic characteristics of three-dimensional structure-soil-structure interaction system，including two identical structures，are investigated to identify the additional effects caused by the presence of a second structure.When comparing the data from the soilstructure system with only one structure and the structure-soil-structure system，two close natural frequencies with opposite phase modes are identified.Therefore，the term twin-frequency is proposed.Next，the value of twin-frequency varying with the frequency ratio of structure to soil is discussed.Meanwhile，the relative distance between two structures and the ratio of foundation width to soil thickness are covered.The data will be used to consider the coupling effects of soil on the dynamic characteristics of structure-soil-structure systems.Finally，a numerical case of seismic response of the structure-soilstructure system is calculated under traveling wave excitations.The numerical results indicate that the twin-frequencies cause beatings of the structures as well as ground motion.

structure-soil-structure interaction；dynamic characteristics；relative distance；frequency ratio；beating

TU311.3

A

1674-4764（2014）03-0092-07

10.11835／j.issn.1674-4764.2014.03.015

2013-12-30

国家自然科学基金（51078032）

潘旦光（1974-），男，研究员，博士，主要从事防灾减灾研究，（E-mail）pdg＠ustb.edu.cn。