新型圆锥曲线组合图规设计及其原理

申艺杰， 陈锦昌

（1. 华南理工大学机械与汽车工程学院，广东 广州 510640；2. 华南理工大学设计学院，广东 广州 510006）

新型圆锥曲线组合图规设计及其原理

申艺杰1， 陈锦昌2

（1. 华南理工大学机械与汽车工程学院，广东 广州 510640；2. 华南理工大学设计学院，广东 广州 510006）

分析了新型圆锥曲线图规（椭圆规、双曲线规和抛物线规）设计的数学原理，利用圆锥曲线的光学性质和几何性质提出了一套图规设计的基本理论，基于这套理论设计出一种新型的、由多个简单连杆型机构零件组合而成的圆锥曲线图规；应用这种组合图规可以规范、快速地绘制出各种工程上常见的二次曲线，弥补了工程制图中一般绘图仪器功能单一的缺点，有较好的应用前景。

工程制图；圆锥曲线；几何性质；图规仪器

绘图是工程技术人员经常性的工作，对一般的直线、圆弧或圆利用常用的尺规作图即可绘制[1]。在几何作图和工程制图中，除了直线、圆弧和圆之外，椭圆、双曲线、抛物线也是常遇到的线形。在绘制这些圆锥曲线时，其常用作图方法现有多段圆弧连接代替、徒手绘画、曲线板描画的方法，前两者近似的作图方法得到的曲线不光滑、难看而且费时，而利用曲线板只能刻画出曲线板上规定参数的曲线，在实际工程制图中很不实用。绘制椭圆的椭圆规有不少，却只能解决椭圆绘制问题，且因为种种设计的局限而目前不能得到广泛地推广。设计人员不得不采用像四圆心法、八圆心法等较为复杂的近似方法，或者必要时采用同心圆法、平行四边行法，并借助于曲线板绘制不准确的椭圆。为了改变这种状态，提高工作效率，长期以来，人们在椭圆规的研制方面曾做了不少工作[2-4]，但由于其结构较为复杂，使用不便，而且只能绘制较大的椭圆，所以一直没有被广泛采用，实用性不强。除椭圆规外，对于其他圆锥曲线的绘制，由于目前还缺乏简单而实用的仪器，更没有能同时绘画椭圆、双曲线和抛物线的常见二次曲线的图规。本文利用圆锥曲线的几何性质和光学性质，提出了一种新型的圆锥曲线图规设计的基本理论，并由此设计出一种新型圆锥曲线图规仪器，该仪器可以规范并且快速地制出各种工程上常见的二次曲线，具有实用性。

1 新型圆锥曲线图规设计的数学原理与仪器构造

1.1 椭圆规的设计原理及构造

1.1.1 椭圆规的设计原理

如图1所示，在以F1、F2为焦点的椭圆上任取一点P，过点P作椭圆的切线，以这条切线为对称轴作出原来椭圆的轴对称图形，当然轴对称图形也是椭圆，这个椭圆的焦点分别是椭圆具有光学性质，即以 F2为焦点射出光线经过椭圆边界反射后经过点F1，再根据反射定律，椭圆在点 P的法线是角 ∠ F2PF1的角平分线，那么就能推出 F1PF′ 共线， F2PF′共线。根据椭圆的性质，椭圆上一点到两个焦点的距离之和为椭圆的长轴长，则 PF1+ PF2为一定值，又因为轴对称的性质有则有性质F1F′= F2F′。保持图形的这一性质，令点P在椭圆上运动，则在生成的动态图形中，有不变量F1F和′，因为两椭圆是全等的，所以′也是不变量。

图1 椭圆规设计原理

以上论证中所用到的相关圆锥曲线几何性质在文献[5-6]中都可以找到，属于数学问题，这里不再证明。下文引用相同，不再赘述。

1.1.2 椭圆规的构造

利用上述的几何原理制作出一套连杆装置，按照图1所示的几何关系，将F1、F2固定，则以四点为铰接点，连上两条定长的杆件再以为铰接点，连上一个定长的杆′则形成一个如图1的机构，该机构在运动过程中′的交点 P的轨迹是一个椭圆。在杆′上刻制出一条轨道槽，轨道槽中存在一个能固定笔芯的滑块于两槽相交处，将滑块的位置限制在点 P的动态位置，则随点 P的运动就可以画出一个椭圆了。

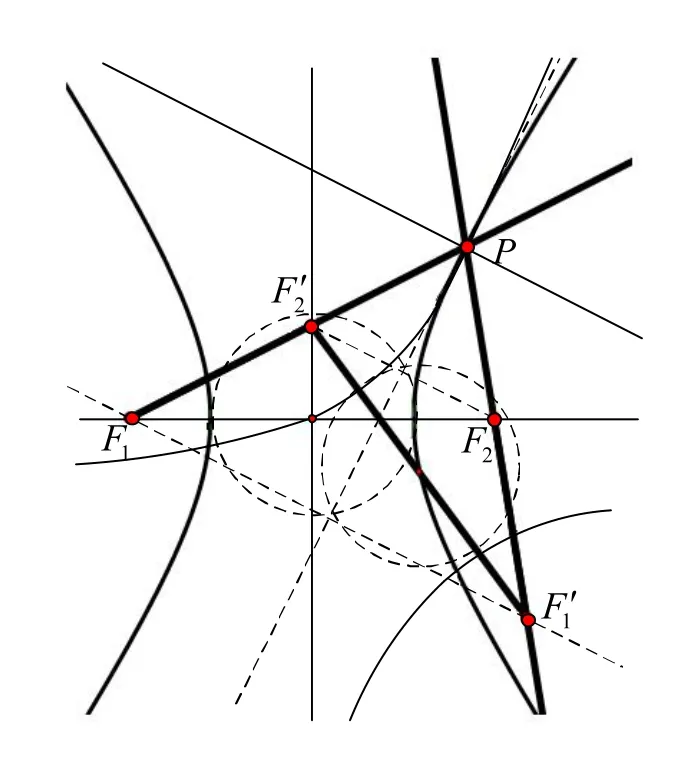
图2 双曲线规设计原理

1.2 双曲线规的设计原理及构造

1.2.1 双曲线规的设计原理

将椭圆换成双曲线，如图2所示，在以 F1、 F2为焦点的双曲线一支上任取一点P，过点P作双曲线的切线，以这条切线为对称轴作出原来双曲线的轴对称图形，轴对称图形是全等的双曲线，这个双曲线的焦点分别是双曲线也具有光学性质，即以 F2为焦点射出光线经过边界反射后，反射光线的反向延长线经过点 F1，再根据反射定律可推知双曲线在点 P的法线是角∠ F2PF1的角平分线，那么就能推出′共线，PF2′共线。根据双曲线的几何性质，双曲线一上点到两个焦点的距离之差为双曲线的实轴轴长，则 PF1- PF2为一定值，又因为轴对称的性质有则有性质保持图形的这一性质，令点 P在双曲线上运动，则在生成的动态图形中，有不变量′和因为两双曲线是全等的，所以则有等腰梯形再由等腰梯形的性质，等腰梯形的两条对角线都相等，又得出两个不变量，这个定值就是双曲线的实轴长。

1.2.2 双曲线规的构造

利用上述的几何原理制作出一套连杆装置，取两支相同的连杆，分别在上打出两个定位孔，这两个定位孔的距离为一定，即是要画出的双曲线的实轴长值，打孔时要注意，其中一个孔打在杆的一端，将它称为端定位点，向另一个方向量出需要的长轴长值，在那个位置打上第二个孔，称为中间定位点，注意杆要取得足够长，余下向另一端延伸方向的区段称为自由段，分别将一个杆的端定位点和另一个杆中间定位点分别在点F1、F2固定，则没有定位的杆上的定位孔位置点分别为即是前一个杆的中间定位点和后一个杆的端定位点。再取一根长度为双曲线焦距的定长杆，以杆上的′为铰接点铰接上去，给机构限制后，则该机构运动过程中的交点P的轨迹是一个双曲线。在杆上的自由段部分刻制出一轨道槽，轨道槽中存在一个能固定笔芯的滑块于两槽相交处，将滑块限制在点P的动态位置，则随着点P的运动，这样就可以画出一条双曲线了。

1.3 抛物线规的设计原理及构造

1.3.1 抛物线规的设计原理

对于抛物线的画法设计要复杂一些，因为抛物线可以看作椭圆和双曲线焦距取为无穷大的极限临界情况，而无穷大是无法用仪器度量的，所以上述的三杆联动画椭圆和双曲线的设计思想应用在这里比较困难。但是按照刚才的设计思路，利用抛物线的光学性质，可设计出一个全等抛物线滚切的动态模型，据此可以设计出抛物线规实现抛物线的制图仪器，原理如下：

如图3所示，在以F为焦点，l为准线，OF为焦准距的抛物线上任取一点P，过点P作切线t，利用抛物线的光学性质可知，从点 F发出的光线以抛物线为镜面反射的光线与轴平行，则可知过点P作轴的平行线就是直线PF关于切线t轴对称线，又根据抛物线的性质，线段PF=PF′即有等腰三角形 ΔP FF′、FF′的垂直平分线是切线 t，由上述分析可知抛物线准线上的一个点与焦点的连线段垂直平分线与过这一点与轴平行的直线的交点轨迹是这条抛物线。

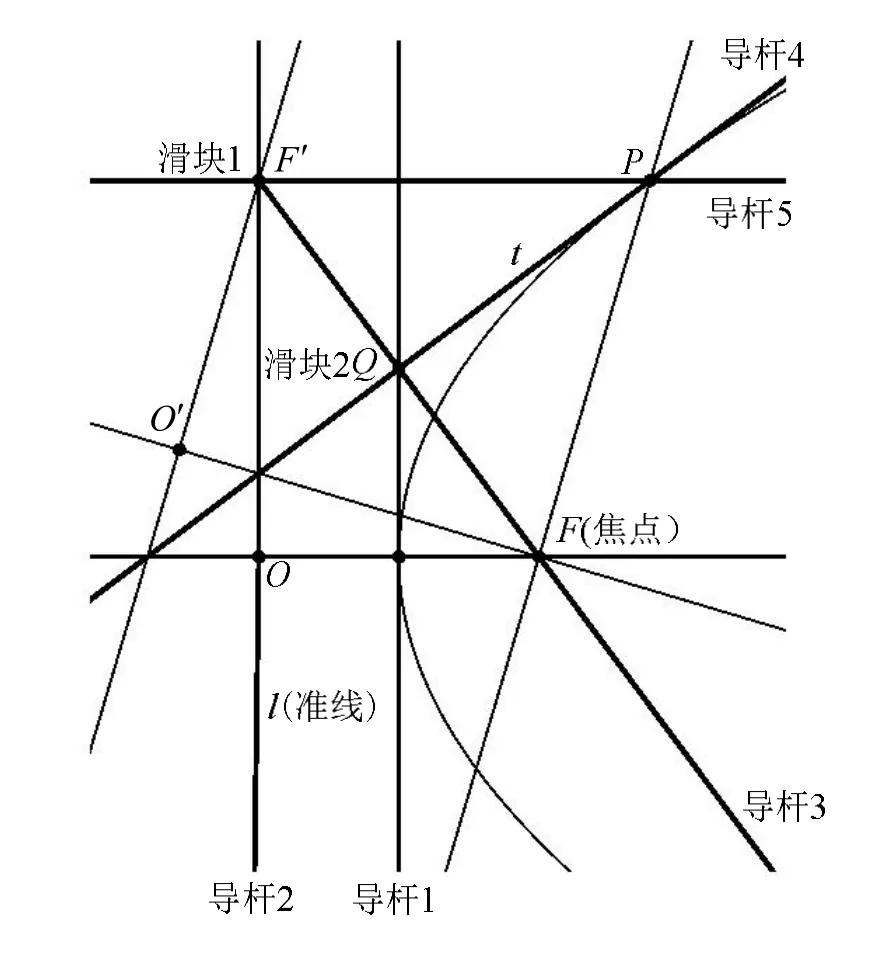
图3 抛物线规设计原理

1.3.2 抛物线规的构造

据上述原理可以设计成抛物线规，因为FF′的中点Q在OF的垂直平分线上，即在抛物线过顶点的切线t1上，也即在过抛物线顶点与轴垂直的直线上，那么就在这根直线的位置上定位一根导杆 1，再在准线位置上定位另一根导杆 2，并在上面加上一个滑块F′，再拿一根自由导杆3，让这根导杆的一端被滑块F′定位，而剩余的自由段被定点F限制，就是说导杆3伴随滑块F′运动而必须经过点F，用一个滑块2记录下导杆1与导杆3的交点位置，取一根导杆4，使导杆4锁在滑块2上，并加锁保持与导杆3垂直，再拿一根导杆5，使导杆5锁在滑块F′上，并再加锁保持与导杆2垂直。这样，在导杆4和导杆5的轨道槽交汇处插上笔芯，随滑块F′在导杆2的轨道上滑动，这支笔芯绘画出一条以F为焦点，l为准线的抛物线。

2 绘制圆锥曲线的组合规

2.1 组合规的组成

在解决完椭圆规，双曲线规，抛物线规的设计原理后，就可以设计出一套组合规绘图工具，利用这套工具的配合使用可以绘制出各种工程需要的圆锥曲线。

组合规（图4）配有的工具（工具名称后的括号内注明的是标准装配中该工具的数量）。

图4 组合规套装示意图

2.1.1 寻迹型导杆

寻迹型导杆是配有旁边带有刻度尺的滑槽轨道导杆，这种导杆的轨道用来给绘图笔以限制画出圆锥曲线，这种导杆称为寻迹型导杆。在每根这种导杆上一端，即为刻度尺零刻度处，装有一个定位钉，另一端开口，可以使滑块滑入导杆轨道里，定位钉的作用是扎在图纸上，使导杆绕着这一点旋转，在工作中这一点是要扎在要画的圆锥曲线的焦点位置。导杆向另一端延伸方向有轨道槽，轨道上可以安置滑块，这个滑块的结构非常特殊，见锁芯滑块。旁边刻有刻度，其结构就像游标卡尺的结构。

2.1.2 限制性导杆

与寻迹型导杆一样，限制性导杆轨道旁也有刻度尺，但从功能角度来讲，限制性导杆的设计长度要比寻迹型导轨的长度要短，因为画双曲线时限制性导杆用来给寻迹型导杆加以限制，而寻迹型导轨的长度决定了绘制双曲线的范围。限制性导杆的结构与寻迹型导杆不相同之处在于，端头没有装定位针。

2.1.3 长导杆

长导杆结构和寻迹型导杆导轨结构不同之处是端头没有定位针，其重要特点是两端开口，轨道上刻有标度尺，上面装配有一块滑块。考虑到用于绘制双曲线和抛物线的范围问题，它比限制性导杆尺度要长一些。长导杆还有一个特点是为绘制抛物线设计的，它的两端可以伸出小图钉，伸出小图钉可以把整个导杆定位在图纸上。

2.1.4 锁芯滑块

锁芯滑块的结构可分多层，每一层套上可以有滑入导轨的凸圈，凸圈通过轴承装配在一个中心轴上。中心轴呈圆筒形，中心是夹槽孔，用来加紧与之配套的铅芯和芯钉。凸圈可以绕中心轴自由转动，凸圈是用来滑入导杆轨道与轨道配合的。每一个凸圈都有一个锁定装置，当一个凸圈滑入轨道时，凸圈沿轨道方向自由运动，而一旦上锁，凸圈就被固定在轨道上一个指定的位置不能移动。夹入铅芯的滑块在滑入两条自由寻迹轨道时，铅芯在纸面上划出轨道交点的轨迹。

2.1.5 凸圈

凸圈套在锁芯滑块上，可以在锁芯滑块上调整套锁位置，它可以滑入轨道槽，与锁芯滑块配合使用，4中已经介绍。

2.1.6 定位芯钉

定位芯钉是与锁芯滑块的夹槽相配合的芯钉，夹入铅芯的滑块定位在滑杆上以后，把钉定在图纸上的一个点，那么这条导杆的运动就被限制为它的轨道必须过定点的运动。

2.1.7 铅芯（数量不作要求，可以按需求增加）

这是与锁芯滑块的夹槽相配合的铅芯，夹入铅芯的滑块在滑入两条自由寻迹轨道时，铅芯在纸面上画出轨道交点的轨迹。

2.1.8 十字定位锁

十字定位锁是专门用来绘制抛物线而设计的工具，结构是有十字槽的方块，两槽方向垂直，中心有圆孔，圆孔的大小与凸圈相配合，槽可以卡在导杆的外沿，两相配合，两根杆卡在槽里时，两根导杆被限制保持垂直。但必须在一定条件下才能加以这样的限制。条件如下：当两根导杆通过滑块的两层凸圈的滑入而配合后，把十字定位锁中心圆孔与上层露出的凸圈相配合后，下方槽卡在下边导杆外沿，这样就可以在上方槽上再拿一根长导杆配合上去，利用长导杆的图钉可以定位上去；也可以不这么做，这样做以后，两根杆运动限制在槽里时，随机械运动两根导杆保持垂直。也可以对上层的杆进行限制，原理相同。

2.2 组合规的使用方法

2.2.1 绘制椭圆

需要工具（按上节的编号给出，括号中注明的是在该绘制工作中所需要此工具的数量，下文同）：1(×2)，2(×1)，4(×3)，5(×6)，7(×1)。

步骤一：找出要画椭圆的两个焦点的位置和椭圆上的一个点，仪器套装中拿出两根寻迹型导杆。两根导杆的定位端钉在图纸上要画的椭圆的焦点位置，将锁芯滑块插好铅芯两层凸圈分别滑入两根寻迹型导杆的导轨，铅芯方向朝向纸面，铅芯位置就在两自由导轨的交点，整个系统构成一个动态机构。

步骤二：拿出一根限制性导杆，利用其上的刻度尺，将其上轨道滑入两个锁芯滑块调至距离为椭圆的焦距，锁定在杆上。

步骤三：将限制性导杆上两个锁芯滑块再加凸圈，使得两滑块可以分别滑入两根寻迹型导杆的轨道槽中，分别在两根寻迹型导轨上的刻度尺上读数，读到要绘制的椭圆半长轴长度处，将对应轨道上的锁芯滑块滑到这个位置用锁定装置锁住。这时三根杆的搭接方式由下层到上层分别为第一根寻迹型导杆、限制性导杆、第二根寻迹型导杆，构成整个动态机构，用手拿住限制性导杆顺着力引动机构，笔芯画出了一个椭圆（图5）。

需要说明的是，当装配好组件如图5所示，把笔芯一开始需要放在椭圆的一个长轴端点。因为杆件不可能无限细，所以笔尖不可能与之完全重合，用仪器旋转绘制后出现一个缺口，该误差可以通过提高制作工艺的精确程度来缩小到可以忽略的程度。然后手动驱动机构逆时针旋转一周，便画出一个圆。

图5 应用组合规画椭圆

2.2.2 绘制双曲线

需要工具：1(×2)，2(×1)，4(×3)，5(×6)，6(×1)，7(×1)

步骤一：找出要画双曲线两个焦点的位置和双曲线上的一个点，仪器套装中拿出一根寻迹型导杆，导杆的定位端钉在图纸上要画的双曲线的一个焦点位置。

步骤二：拿出一根限制性导杆，在其轨道上滑入两个锁芯滑块，利用其上的刻度尺，一个定位到轨道端头，另一个定位到刻度在一个焦距的位置，并且将这个滑块通过在加套一个凸圈的方法滑入步骤一中寻迹型导杆的轨道中。

步骤三：拿出又一根限制性导轨，通过在加套一个凸圈的方法将位于限制性导杆端头的滑块滑入其中。

步骤四：拿出两个锁芯滑块，分别滑入步骤三中的限制性导杆的轨道中，向先滑入的那个锁芯滑块里插入定位芯钉，并在限制性导杆的刻度尺上读数到双曲线的实轴长的位置，向后滑入的锁芯滑块插入铅芯并通过在加套一个凸圈的方法滑入步骤一中寻迹型导杆的轨道中。这时将定位芯钉钉在双曲线的另一个焦点上，三根杆的搭接方式由下层到上层分别为第一根寻迹型导杆、第二根寻迹型导杆、限制性导杆，构成整个动态机构，用手拿住限制性导杆顺着力引动机构，笔芯画出了一支双曲线（图6）。

需要说明的是，这里绘制出来的双曲线范围决定于寻迹型导杆的长度，可根据工程的需要，采用不同规格的套规进行绘制。

图6 应用组合规画双曲线

2.2.3 绘制抛物线

需要工具：1(×4)，3(×2)，4(×3)，5(×6)，7(×1)，8(×3)

步骤一：找出要画抛物线的焦点位置、准线位置和顶点切线的位置（顶点切线与准线平行，焦点到顶点切线的距离和顶点切线到准线的距离相同，都是半个焦准距的长度）。然后从仪器套装中拿出两根长导杆，两根长导杆两端伸出图钉，把两根杆轨道分别定位到准线位置和顶点切线位置。

步骤二：拿出一根限制性导杆，使被固定在图纸上的两根长导杆的两个滑块的另端凸圈按先准线位置上的导杆，再顶点切线位置的导杆的顺序滑入限制性导杆的轨道里，向限制性导杆轨道里滑入一个加有定位芯钉的滑块，再把定位钉钉在焦点处，注意滑块对导杆都不定位。

步骤三：拿出两个十字定位锁和两根长导杆，在准线位置长导杆上的滑块处利用十字定位锁运用垂直限制加上一根过该滑块对应点与准线垂直的长导杆，再在顶点切线位置长导杆上的滑块处利用十字定位锁运用垂直限制加上一根过该滑块对应点与限制性导杆垂直的长导杆。拿出一个夹紧铅芯的滑块滑到这两根长导杆里，笔迹即是长导杆轨道交点轨迹，就是抛物线（图7）。手握准线位置倒杆上的滑块上下运动控制机械即可。

图7 应用组合规画抛物线

2.2.4 绘制圆

圆也属于圆锥曲线，要画出半径为R的圆，取一根寻迹型导杆，把它一端定位在圆心处，向轨道中滑入插好笔芯的滑块到刻度尺半径 R处，手持导杆旋转一周即可。

3 结 束 语

本文从圆锥曲线的几何性质和光学性质出发，分别给出了椭圆规、双曲线规和抛物线规设计的数学原理及图规构造，设计出一种新型的圆锥曲线组合图规仪。该设计弥补了常见的传统椭圆规功能单一的缺陷，能够绘制出工程制图中不同的基于焦点的各种参数的平面二次曲线（即已知焦点的位置）。本设计的圆锥曲线图规操作简单，易于推广，具有一定实用性。

该产品还没有进行商业化，还在实验测试阶段，整套机械主要运用的都是简单平面连杆机构，所以操作简单易于制作，利用文献[7]中的方法进行机构分析，可以进一步验证各处机构的科学性、合理性。目前在实验室中连接的简易模型工作状态良好，可以绘制出上文要求的各种圆锥曲线，绘图区域的大小由杆件的长短控制，可以批量生产出不同规格的适用于不同绘图区域要求的套装，随着机构的精细程度提高，可以提高它的绘图精度，未来的开发和应用价值可佳。

[1] 马希青. 机械绘图工具和仪器的使用方法[M]. 北京:机械工业出版社, 2010: 2-20.

[2] 曾毅慧. 椭圆规设计中的一些问题及解决途径[J].机械工程师, 1988, (6): 20-22.

[3] 高利宏. 一种椭圆规的设计及附加功能介绍[J]. 机械设计, 1997, (8): 44.

[4] 杜密科, 刘淑先. 两种椭圆规机构的设计及原理[J].机械工程师, 1995, (4): 18-19.

[5] A·科克肖特, F·B·沃尔特斯. 圆锥曲线的几何性质[M].蒋声译. 上海: 上海教育出版社, 2002: 1-27, 34-122.

[6] [古希腊]阿波罗尼奥斯. 阿波罗尼奥斯圆锥曲线论[M]. 朱恩宽等译. 西安: 陕西科学技术出版社, 2007: 244-318.

[7] 华大年, 华志宏. 连杆机构设计与应用创新[M]. 北京: 机械工业出版社, 2008: 194-288.

A New Design of Combinational Conical Curve Gauge and Principle of Chart

Shen Yijie1, Chen Jinchang2
(1. Machinery and Automobile Engineering Institute, South China University of Technology, Guangzhou Guangdong 510640, China; 2. School of Design, South China University of Technology, Guangzhou Guangdong 510006, China)

Through analyzing mathematical principles of designing the conical curve gauge (ellipse gauge, hyperbola gauge and parabola gauge), a set of design theory is put forward based on the optical and geometric properties of conical curve. By applying this theory, a new type of conical curve gauge is designed, which is composed of multiple simple linkage mechanical parts assembly, and which can help quickly draw various normative conical curves common in engineering. It makes up for the disadvantage that the function of general engineering drawing instrument is single and has a good prospect of application.

engineering drawing; conic curve; geometrical properties; compasses instrument

O 17

A

2095-302X (2014)02-0208-06

2013-03-25；定稿日期：2013-07-01

湖南省教育厅资助项目（12C0118）；湖南科技大学教研资助项目（G31022）

申艺杰（1992-），男，河南洛阳人，本科生。主要研究方向为机械工程及自动化。E-mail：syj92929@163.com

陈锦昌（1956-），男，广东南海人，教授，硕士。主要研究方向为工程图学、计算机图形学、工业设计。E-mail：jcchen@scut.edu.cn