一种权值约束的精确配准算法
蒋睿嵩, 魏发远, 冯大勇, 闫茂振
(中国工程物理研究院总体工程研究所,四川 绵阳 621900)
一种权值约束的精确配准算法
蒋睿嵩, 魏发远, 冯大勇, 闫茂振
(中国工程物理研究院总体工程研究所,四川 绵阳 621900)
针对数据与模型的精确配准问题,提出一种权值约束的配准算法,通过对配准点施加不同的权值,利用权值约束保证模型重要区域的配准精度。首先,论文基于经典配准模型,引入权重因子,建立了改进的权值约束的配准模型。针对配准模型的求解问题,通过对现有SVD-ICP算法进行适应性改进,提出并研究了带权SVD-ICP(wSVD-ICP)算法,重点推导了基于wSVD算法求解旋转矩阵R和平移矩阵T的过程。最后,论文利用仿真数据和实测数据对配准模型进行了验证;计算结果表明,论文所提算法通过对精度要求较高区域分配高权值进行约束,可有效提升该局部区域的配准精度;同时,可在一定程度上改进整体配准精度和效率。
配准;权值;约束;wSVD-ICP
模型配准作为计算机图形图像领域的基本技术之一,目前已广泛地应用于三维重构、机器人视觉、模式识别、几何处理以及CAD/CAM等领域[1-2]。模型配准实际上就是求解待配准模型与理论模型之间的最优空间变换,使待配准模型通过这个最优空间变换得到新的数据模型与理论模型满足相似度测量要求。模型之间的变换可分为刚性变换和非刚性变换两类[3];对于工业领域的产品形状检测而言,需将产品视为刚体,因此,论文重点研究刚体的精确配准问题。
迭代最近点(Iterative Closest Point, ICP)算法[1,4]是刚体配准中最为典型的算法之一。ICP算法通过求取最小平方来减小每一次迭代过程中对应点集的平均误差,以及通过查找最近邻点来减小对应点对之间的距离。ICP算法虽然存在局部收敛的问题,但是由于其概念清晰、收敛性较好等优点,得到了广泛的关注。许多学者从点对选取、点对匹配和最小化策略等方面,对ICP算法进行了改进[5];如Fitzgibbon[6]提出了LM算法对ICP算法进行加速,Jost和Hugli[7]提出了一种多分辨率的 ICP算法以提高算法的速度和鲁棒性,Phillips等[8]提出一种分段ICP算法以检测并删除参与配准的异常点。此外,也有研究人员对ICP算法进行改进,并将其应用于非刚体配准[9-10]。
在实际工程应用中,配准模型的不同区域往往具有不同的重要度。例如,在产品检测中,不同区域有不同的设计公差,理想的配准函数应该保证公差要求较高区域的配准精度,而适当放宽公差带较宽区域的配准精度。
为此,通过引入权值约束的概念,通过对配准模型中较为重要的区域赋予较高的权重,从而实现模型的高精度配准。在已有的研究中,权值的设置主要是为区分点集是否参与配准[6],权值也仅有0和1。针对该问题,论文首先基于经典的配准目标函数,研究了改进的带权配准目标函数;在此基础上,针对目标函数的优化求解,提出了一种改进的 SVD-ICP算法求取模型配准参数;最后,通过两个配准算例,对算法进行验证分析。
1 权值约束的配准模型

对于待配准模型和理论模型的空间配准问题,就是要找到合适的空间变换参数,使得目标函数最小。基于基本的配准目标函数F1,建立权值约束的配准目标函数F2,如式(2)所示:其中,式(2)中引进了约束权因子,被定义为参与配准的点集的重要程度;公式中N为参与配准的点数;Pi(i=1,2,…,N)为待配准模型上的点;Qi为Pi在CAD模型曲面上的投影点;wi是约束权因子;R为旋转矩阵;T为平移矩阵。
对配准模型的优化,其实质即为通过令目标函数最小,得到 6 个最优配准参数(α,β,γ,Tx,Ty,Tz),其中前3个变量为绕X、Y、Z轴的角度参数,也就是所谓的Euler角。后3个变量为沿X、Y、Z轴的平移参数。通常,旋转矩阵和平移矩阵分别表达为式(3)、式(4):
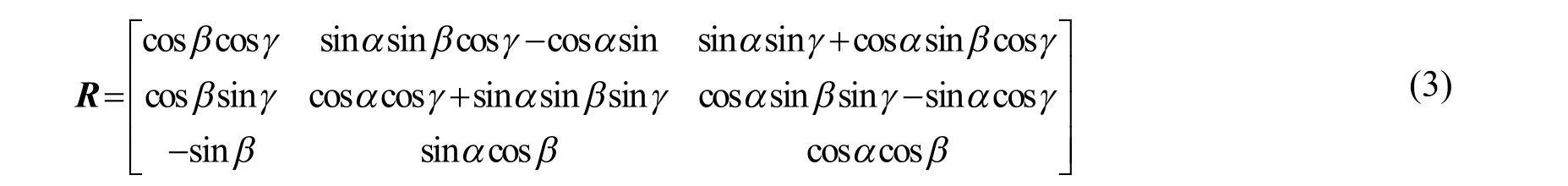
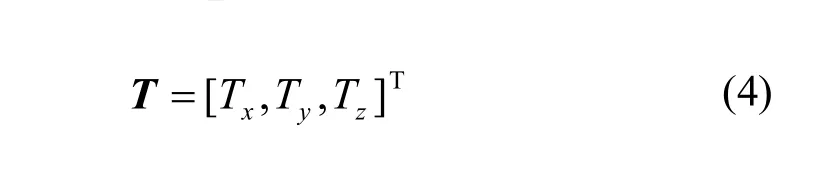
2 模型求解算法
针对带权值约束的配准目标函数的求解问题,提出并研究一种权值约束的 SVD-ICP算法(wSVD-ICP),该方法具有迭代收敛速度快、配准精度高等优点。论文首先研究wSVD-ICP算法的基本步骤,在此基础上,重点研究基于wSVD算法的空间变换参数计算方法。
2.1 wSVD-ICP算法步骤
对于预先得到的待配准模型和已知的理论模型,要得到待配准模型相对理论模型的变换矩阵,基于wSVD-ICP求解算法的迭代步骤一般如下:
步骤1初始化变换矩阵R0、T0。
步骤,2k 为 求迭取代变次换数后:的待配准模型(i=1, 2, … ,N)

步骤3计算与待配准模型(i=1,2, …,N)对应的理论模型上的最近点(i=1,2,…,N)。
步骤4基于wSVD分解算法,由和对变换矩阵 Rk-1、 Tk-1进行更新得到 Rk、Tk。
步骤5计算待配准模型与理论模型间的偏差 εk:

步骤 6如果 εk<δ(δ为预先指定的迭代阈值)或者达到最大迭代次数,退出;否则令k=k+1,转步骤2。
2.2 wSVD算法
针对权值约束的配准目标函数求解问题,对现有 SVD算法进行改进,通过加入权值约束,实现模型的精确配准。该算法在给定配准控制点集{Pi}、{Qi}(i=1,2,…,N)的前提下,可计算两个待配准模型之间的旋转变换R与平移变换T。
针对式(2)所示的配准目标函数,按式(7)计算待配准模型 Pi( i= 1,2,…,N)及其在理论模型上的对应点集 Qi(i= 1,2,…,N)的带权质心:
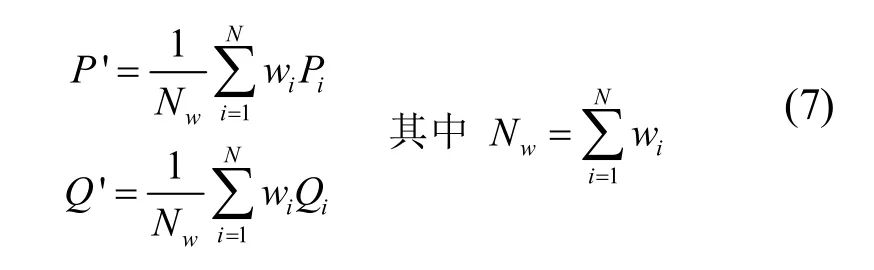
其中, wi为配准点 Pi所对应的权值。
利用式(8),计算这两个数据集合中每一个数据点相对于质心的位移。

将式(8)代入式(2),可得:

将上式的右边展开,得到:

通过简单数学推理可知,F2最小等价于F最大:

式中:

根据Lemma定理,对任何正定矩阵 AAT和正交矩阵B,有如下结论(证明过程参见文献[11]):
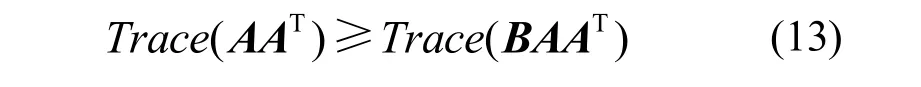
令H的奇异值分解为:

这里U和V是3×3正交矩阵,Λ是3×3具有非负元素的对角矩阵,令:
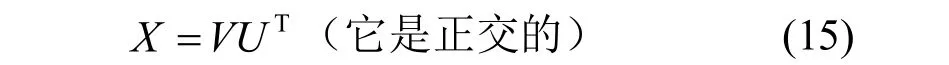
于是有:
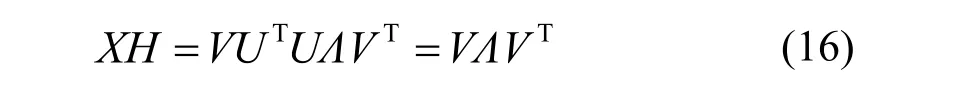
它是对称和正定的。因此根据Lemma定理,对任何3×3正交矩阵B:
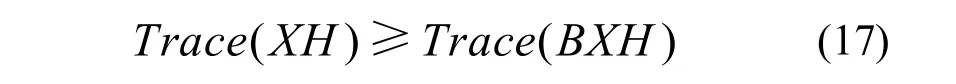
这样,在所有3×3正交矩阵中,X使F最大,也就是使 F2最小。
根据上述讨论,权值约束的 SVD算法步骤为:
步骤1根据配准控制点集按照式(7)计算两个待配准模型的质心 P'、 Q′。
步骤2利用式(8)计算这两个配准控制点集合中每一个数据点相对于质心的位移。
步骤3根据式(12) 计算3×3矩阵H,并对矩阵H进行奇异值分解得到式(14)。
步骤4计算旋转矩阵R:

步骤5计算平移矩阵T:

3 算例验证与比较分析
本节设计两个具体算例对论文所提的配准算法进行有效性验证。两个算例都以涡轮叶片截面点作为实验对象。其中,算例一为仿真数据,直接从理论模型上截取后进行空间变换得到,其几何形态与理论模型完全一致,如图1所示。算例二为实际叶片的三坐标测量数据,其几何形态与理论模型存在一定的差异,从而可更好地验证权值约束的配准模型对待配准数据重要部位的配准精度提升能力。根据工程设计知识,叶片越厚的部位(叶盆和叶背部位)公差越大,对配准的精度要求相对较低;叶片越薄的部位(前缘和后缘)公差越小,对配准的精度要求相对较高,如图2所示。因此,配准点的权值以最小壁厚处为1,其余各点权值为此处壁厚除最小壁厚所得值,配准点权值分布,如图3所示。
3.1 基于仿真数据的算例验证
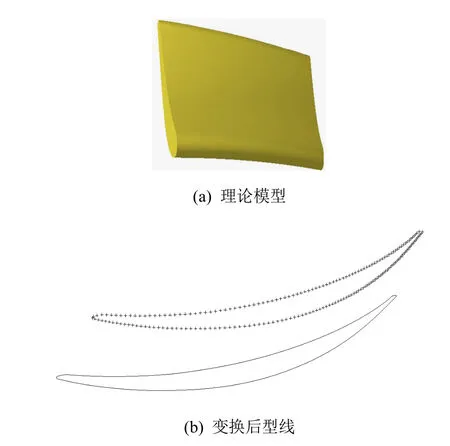
图1 仿真数据

图2 实测数据
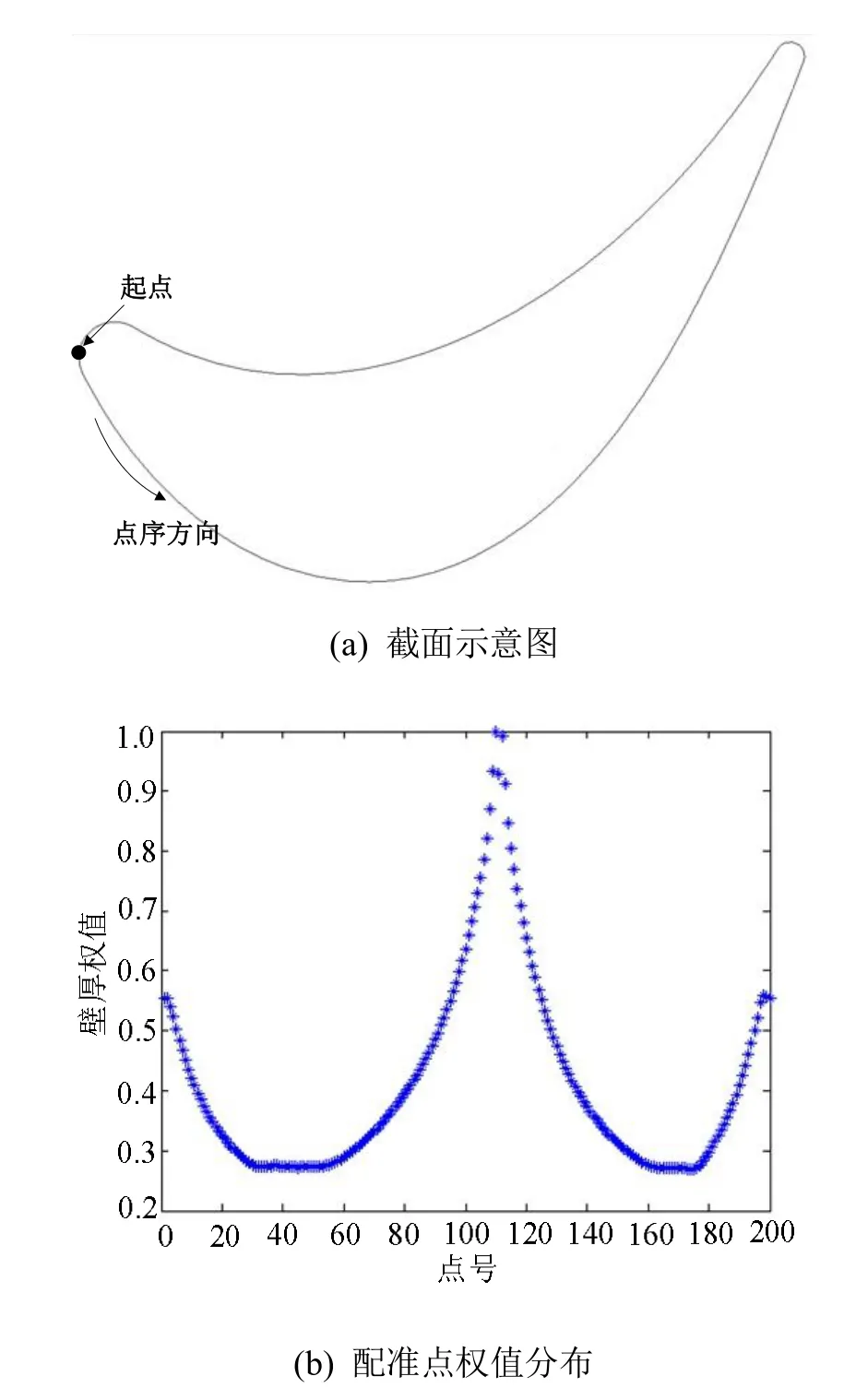
图3 叶片截面配准点权值分布图
本算例以仿真数据为实验对象,考察权值约束的配准模型对截面线的配准效果。仿真数据构造方法为:从截面线提取200个配准控制点并进行空间坐标变换。不失一般性,同时考虑到ICP算法容易陷入局部最优的问题(论文主要解决权值配准问题,因此对局部最优问题不作讨论),设定较小的变换参数如表1所示。通过变换得到仿真数据,该仿真数据与理论模型只存在空间变换关系,其几何形态完全一致。配准结果及相关数据列出如表 2所示,程序执行环境为:Intel Core2 2.33GHz,2GB RAM,NVIDIA GeForce 8600GT。

表1 仿真数据变换参数
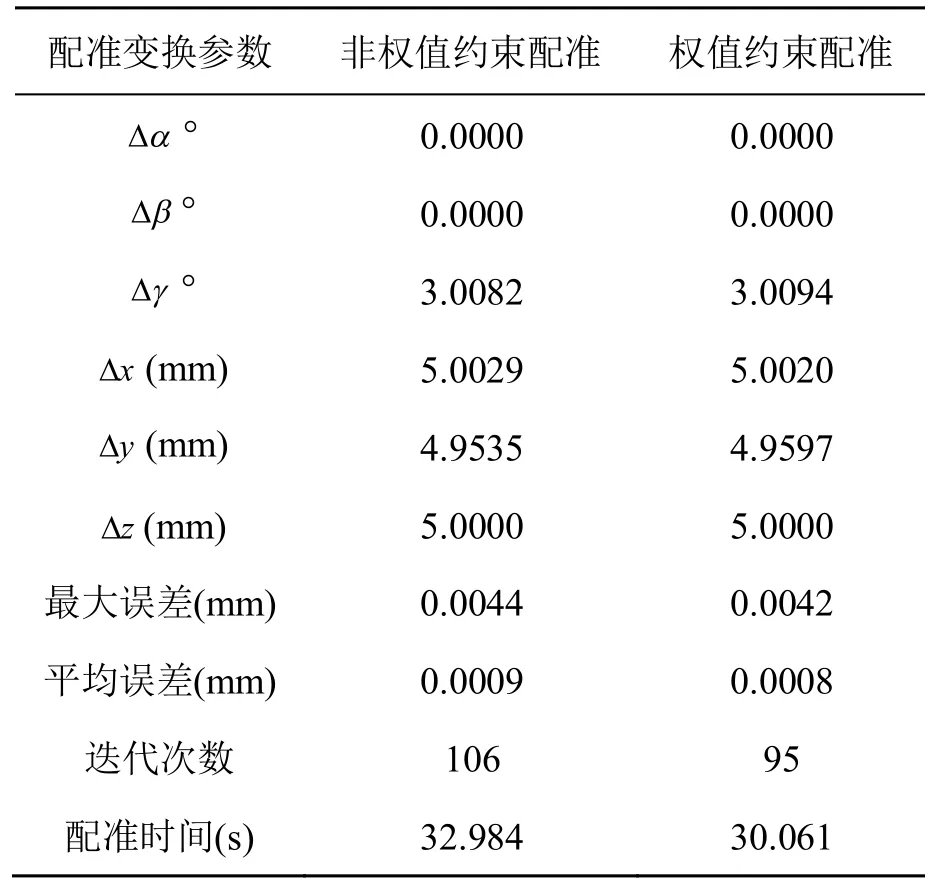
表2 仿真数据变换参数对比
从表2中的数据可以看出,由于配准模型与理论模型几何形态完全一致,权值约束对配准精度的影响表现得并不明显。但是,在有权值约束的情况下,模型配准结果的最大误差、平均误差以及迭代次数都略小于无约束情况,从而说明有约束与无约束情况相比,不仅配准后模型更逼近理论模型,也提高了收敛速度,改善了配准效率。
3.2 基于实测数据的算例验证
通过实测涡轮叶片截面线形成配准模型。在此基础上考察配准模型同理论模型的配准结果,从而验证权值约束的配准算法对变形数据的配准效果。采用 wSVD-ICP算法进行配准模型求解,得到的配准变换参数如表3,迭代收敛过程如图4所示。
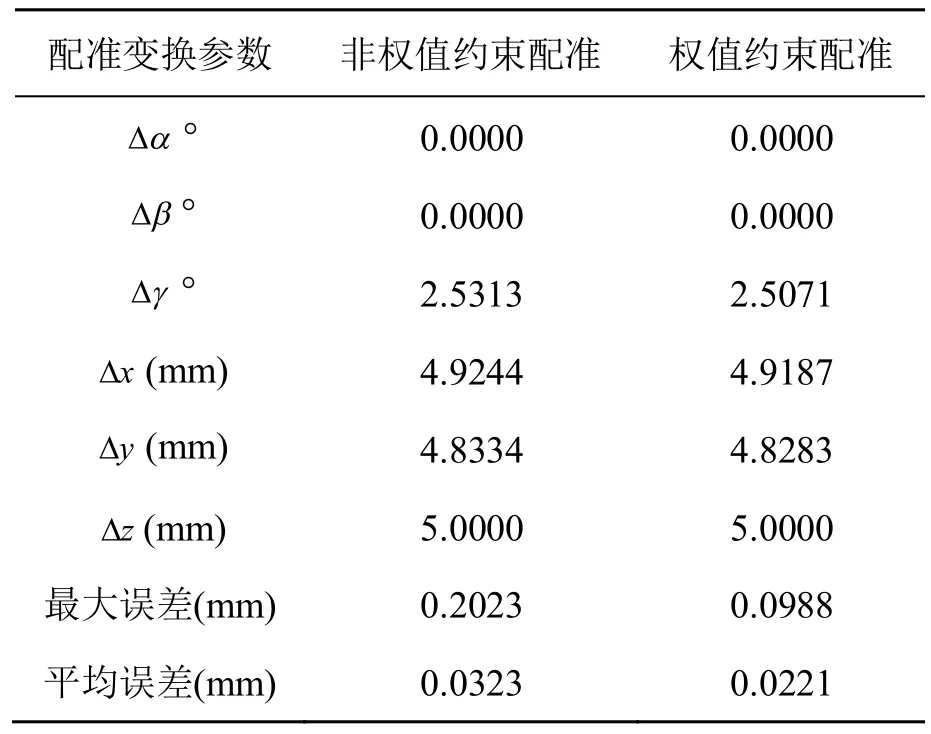
表3 加权配准与非加权配准的变换参数

图4 权值约束与经典配准算法对比
从表3可以看出,使用权值约束的配准模型,配准后的最大误差及平均误差均小于标准配准模型。此外,从图4可以看出,两种配准模型的收敛速度相当。但是,使用加权配准模型,其主要目的是为保证截面线前、后缘处的配准精度,因此,需要进一步考察论文算法对公差精度要求较高区域的变形抑制效果。两种模型的配准控制点相对于理论模型的误差,如图5所示,从图中可以看出,权值约束的配准模型通过将型线前、后缘处的误差转移到叶盆、叶背区域,有效的保证了截面线前、后缘的配准精度。

图5 配准误差分布图
4 结 论
针对产品测量数据的配准问题,在分析现有配准算法的基础上,提出了一种权值约束的模型精确配准算法。通过在配准目标函数中引入权值约束,利用权值控制优化算法的搜索方向,从而可有效保证精度要求较高区域的配准精度。针对配准目标函数的优化求解,论文在经典SVD-ICP算法的基础上,研究了wSVD-ICP算法。最后,论文利用仿真数据和实测数据设计了两个算例对权值约束的配准模型进行了验证,实验结果表明:
(1)针对待配准模型同理论模型一致的情况,权值约束的配准算法在配准的精度和效率上略优于传统配准算法。
(2)针对待配准模型同理论模型不一致的情况,通过权值约束的配准算法,可将配准精度向公差要求较高区域转移,从而提升公差要求较高区域的配准精度。
此外,由于ICP算法的固有特性,本文算法可能陷入局部最优。为避免此问题,可将配准分为粗配准和精配准两步,初配准采用GA等全局优化算法,在精配准阶段采用本文算法。同时,本文的研究主要针对刚体配准展开,对非刚体配准,论文算法并不适用,需要在此基础上进行改进,这也是进一步的研究工作之一。
[1] Besl P J, McKay N D. A method of registration of 3D shapes [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-255.
[2] Li Hongdong, Hartley R. The 3D-3D registration problem revisited [C]//IEEE 11th International Conference on Computer Vision. Rio de Janeiro, 2007: 1-8.
[3] Myronenko A, Song X. Point set registration: coherent point drift [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275.
[4] Zhang Z. Iterative point matching for registration of free-form curves and surfaces [J]. International Journal of Computer Vision, 1994, 13(2): 119-152.
[5] Rusinkiewicz S, Levoy M. Efficient variants of the ICP algorithm [C]//IEEE Third International Conference on 3-D Digital Imaging and Modeling. Quebec City, 2001: 145-152.
[6] Fitzgibbon A W. Robust registration of 2D and 3D point sets [J]. Image and Vision Computing, 2003, 21(13): 1145-1153.
[7] Jost T, Hugli H. A multi-resolution ICP with heuristic closest point search for fast and robust 3D registration of range images [C]//IEEE Fourth International Conference on 3-D Digital Imaging and Modeling. Alberta, 2003: 427-433.
[8] Phillips J M, Liu R, Tomasi C. Outlier robust ICP for minimizing fractional RMSD [C]//IEEE Sixth International Conference on 3-D Digital Imaging and Modeling. 2007: 427-434.
[9] Du Shaoyi, Zheng Nanning, Ying Shihui, You Qubo, Wu Yang. An extension of the ICP algorithm considering scale factor [C]//IEEE International Conference on Image Processing, 2007: 193-196.
[10] Du Shaoyi, Zheng Nanning, Ying Shihui, Liu Jianyi. Affine iterative closest point algorithm for point set registration [J]. Pattern Recognition Letters, 2010, 31(9): 791-799.
[11] 刘 晶. 叶片数字化检测中的模型配准技术及应用研究[D]. 西安: 西北工业大学, 2006.
A New Weight Constraint Precision Registration Algorithm
Jiang Ruisong, Wei Fayuan, Feng Dayong, Yan Maozhen
(Institute of Structural Dynamic, China Academy of Engineering Physics, Mianyang Sichuan 621900, China)
Aiming at the precision registration, a registration algorithm with weight constraint is studied in this paper. This algorithm can ensure the registration accuracy by imposing different weights to different registration points. First, the registration model with weight constraint is established by introducing weight factor into traditional registration model. Second, in order to solve the registration model, a weight constraint SVD-ICP algorithm (wSVD-ICP) is studied based on the classical SVD-ICP algorithm. Especially, the detailed solving process of rotation matrix R and transform matrix T based on wSVD algorithm is shown. At last, two applications are presented for demonstration by using simulation data and measuring data respectively. The results indicate that the algorithm employed in this paper can improve the local registration accuracy significantly by assigning high weight to the high precision demand registration points. Moreover, the algorithm can improve the global registration accuracy and efficiency.
registration; weight; constraint; wSVD-ICP
TP 391
A
2095-302X (2014)02-0167-06
2013-06-12;定稿日期:2013-09-06
蒋睿嵩(1984-),男,四川安岳人,博士。主要研究方向为计算机辅助设计、复杂产品结构优化设计技术。E-mail:ruisong.jiang@gmail.com
冯大勇(1970-),男,四川阆中人,高级工程师,硕士。主要研究方向为计算机辅助设计、设计制造一体化技术。E-mail:fdyuse@163.com

