海浪实时绘制中波浪谱的选择
陈丽宁, 金一丞, 任鸿翔
(大连海事大学航海动态仿真与控制交通行业重点实验室,辽宁 大连 116026)
海浪实时绘制中波浪谱的选择
陈丽宁, 金一丞, 任鸿翔
(大连海事大学航海动态仿真与控制交通行业重点实验室,辽宁 大连 116026)
Phillips谱是海浪实时绘制中常用的波浪谱。首先分析了Phillips谱的结构,指出该谱是一个瞬时空间谱,其频率谱符合Neumann形式,与P-M谱接近,其方向分布函数为国际拖曳水池会议推荐的形式。令P-M谱与Phillips谱具有相同的单位面积波能,给出了Phillips谱风速的确切含义并计算出该谱的常数。除了使用Phillips谱,还尝试其它形式的谱。用P-M谱和cos-2s形式方向分布函数构造了瞬时空间谱PM-cos2s形式,用JONSWAP谱和Poisson形式方向分布函数构造了瞬时空间谱J-Po形式。比较3种谱的绘制结果发现,使用Phillips谱、PM-cos2s谱的绘制结果均能反映风速对海浪的影响,不能反映风距的影响,使用 J-Po谱的绘制结果既能反映风速、也能反映风距对海浪的影响,且三者的绘制帧率一致。如果要选择适合航海模拟器中海浪绘制的瞬时空间谱,该谱的风参数既应包括风速,也应包括风距,且生成波应在风向的(-π,π]范围内,因此J-Po谱在三者中最适合航海模拟器。绘制结果已应用于航海模拟器中。
海浪绘制;Phillips波浪谱;方向分布函数;风速
自然场景中海浪的实时绘制,在计算机动画、虚拟现实等领域有着广泛地应用,对航海仿真而言其重要性更是不言而喻的。海浪场景的绘制是复杂的,一直是计算机图形学研究领域的热点之一。
Mihalef等[1]指出海浪的绘制可分为 3个尺度,其中精细尺度为飞溅和泡沫、中间尺度为水面的波纹、大尺度为波浪的翻转和破碎。目前海浪的绘制方法主要包括两大类:基于物理模型的方法和基于构造的方法。
基于物理模型的方法以纳维-斯托克斯(Navier-Stokes, N-S)方程为基础。对其描述又可分为两类[2],拉格朗日法和欧拉法。两种方法的着眼点不同,拉格朗日法着眼于流体质点,是一种基于网格的方法;欧拉法着眼于流场空间的点,是一种基于粒子的方法。N-S方程描述了流体的运动。使用基于物理模型的方法时,通过求解N-S方程,可以计算得到流体本身的静止状态和运动状态的特性(包括速度、压强、密度等参数的变化),以及流体和相邻固体间的相互作用和流动规律。因此,对于液体的模拟,基于物理模型的方法适合于模拟自由液面、混合流、多相流、固液耦合等[3-5]。然而在解算 N-S方程的时候需要耗费大量的计算机资源,因此,基于物理模型的方法通常用于绘制中、小尺度的液体,而且实时性较差。
构造法可以分为两类:基于几何模型的方法和基于统计与谱的方法。基于几何模型的构造法主要是通过摆线、正弦曲线等模拟海浪几何形状[6-8]。该方法比较简单,可以实现大规模海浪场景的实时绘制(帧率大于30f/s),但风等初始条件相同时每次绘制的海浪在同一位置初始波高相同,绘制的波浪是重复的,过于规则,与实际情况不符。基于统计与谱的方法首先对波数进行采样,用波浪谱计算对应的波数域波幅,然后对波数域波幅进行二维快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT),获得位置域波幅和水平方向位移,进而在位置域构造海浪[9-14]。
Michel[10]提出了一种多尺度 IFFT的海浪模拟方法,在比较粗糙的网格上采用IFFT生成海浪的高度图,在精细的采样网格上生成波浪的法线图来实时计算海浪光照,模拟了航迹以及浅水区的波浪衰减现象。在IFFT构造海面的基础上,任鸿翔[11]采用同心圆网格模型对海面进行采样,减轻了瓷砖效应,赵欣和裴炳南[12]使用了投影网格模型提高绘制效率。与基于几何法不同,使用该方法时,当风等初始条件相同时每次绘制的海浪在同一位置初始波高都不同,绘制结果具有随机性。由于海浪本身可以看作一个随机过程[13-14],因此该方法更接近实际情况。该方式适合于绘制充分发展的海浪,可以实现大规模海浪场景的实时绘制。
联合国国际海事组织(International Maritime Organization, IMO)在海员培训、发证和值班标准国 际 公 约 (the International Convention on Standards of Training, Certification, Watchkeeping for Seafarers, STCW convention)中鼓励在海员培训、评估中使用模拟器[15-16]。挪威船级社(Det Norske Veritas, DNV)在其2.14标准[17]中要求在航海模拟器中使用波浪谱绘制海浪。与其他的海浪绘制相比,应用于模拟器的绘制海浪需要面对两个问题:①实时绘制大规模海浪场景;②绘制结果要能够准确体现风对于海浪的影响。所谓大规模海浪场景,指的是绘制海域面积大(有时要若干平方公里)。所谓实时绘制,指的是绘制场景时要保证一定的帧率,使得绘制效果连续,通常要求帧率在30f/s以上[17]。风对于海浪的影响,主要体现在风对于绘制海浪的波高、传播方向等方面的影响。则在上述的方法中,基于统计与谱的方法更适合于航海模拟器中海浪的绘制。因此,本文选择该方法绘制海浪。
1 基于Phillips谱的海浪绘制
1.1 算法简介
在三维世界坐标系xyz中,平面xz平行于海平面,y轴垂直于海平面,向上为正。令水平位置向量 x=(x,z);波数向量 k=(kx,kz)=(k cosθ, k sinθ),其中θ为向量k与x轴正半轴夹角;风速向量 u=(ux,uz)=(U cosα, U sin α),U为风速大小,α为风速与x轴正方向的夹角。在航海学和气象学中,风向是风吹来的方向[18],记为 α',α与 α'的关系如下:

则t时刻水平位置x的波幅为:


其中*表示复数取共轭。根据色散关系,在深水中波数和频率有如下关系:
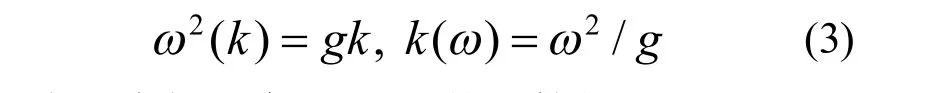

其中 εr和 εi为独立的均值为0、方差为1的高斯随机数; Ph(k)为Phillips谱,即:

如果仅仅通过上述计算获得海浪的高程,所绘制的海浪在几何上是对称的。但实际的海浪在几何上是不一定对称的,当波浪陡度在局部增加时,波峰会变得更加尖锐,波谷会变得平坦[13]。为了达到这一效果,需要引入Choppy波。Choppy波模型源自线性波变换产生的视觉效果。它的主要优势是把简洁性、稳定性、准确性进行了融合[19]。在基于Phillips谱绘制海浪的方法中,需要使用(k ,t)来计算二维位移矢量场,如下式:

其中,符号Im表示取其后括号内表达式的虚部。使用该矢量场,波面网格点的水平位置为x +λD(x ,t )。λ为一常数,用于衡量位移向量重要性。使用Choppy波不会直接改变波幅,而是根据波幅的空间结构来扭曲表面点的水平位置。这种方法使得波峰部分变得尖锐,波谷部分变得平缓,绘制结果更加逼真。
1.2 应用Phillips谱所遇到的问题
虽然 Phillips谱在绘制海浪中已经得到广泛应用[9-12],但使用过程中还会遇到一些问题。其一,常数A的取值或取值准则没有给出。其二,对风速没有详细说明,风速随距海面的高度变化而变化,因此在波浪谱中,都会对风速加以说明。例如,Neumann谱所用风速为距离海面7.5m高度处的风速,P-M谱的风速为距离海面19.5m高度处的风速,JOWNSWAP谱所用风速为距离海面10m高度处的风速。
在本文第2节中,首先分析了Phillips谱的频率谱和方向分布函数,令Phillips谱和P-M谱具有相同单位面积波能计算出Phillips谱常数A,并参考P-M谱说明了Phillips谱风速的高度。考虑到Phillips谱不能反映风距对海浪的影响,第3节则构造了其他形式的波浪谱来绘制海浪,使得绘制结果不仅能反映风速、风向对海浪的影响,还能反映风距对风浪的影响。第4节对所用谱的绘制结果进行比较,并总结出什么样的谱适合于航海模拟器。
2 Phillips谱的结构
为了解决上面提到的 Phillips谱存在的问题,需要对Phillips谱的结构作更深入的分析。本节首先介绍了频率谱、瞬时空间谱和方向谱的概念,进而分析了Phillips谱的频率谱和方向分布函数,在此基础上计算了常数A,并说明采用风速的高度。
2.1 频率谱、瞬时空间谱和方向谱
ξ(x ,t )位置为x的点在t时刻的表面位移,ξ的自相关函数为:符号表示取期望值。若 ω∈ (0,∞ ),记 S(ω)为:

若 ω∈ (- ∞,∞ ), S(ω) 为:

则 S(ω)称为频率谱,其量纲为 L2T。在量纲中,L表示长度量纲,T表示时间量纲。
记瞬时空间谱Ψ (k)为:

Ψ(k)的量纲为 L4,且:

由于k和ω存在一定的关系,则:

上式中积分因子由k变为ω和θ。令E(ω,θ)为方向谱,则方向谱和瞬时空间谱的关系为[14]:
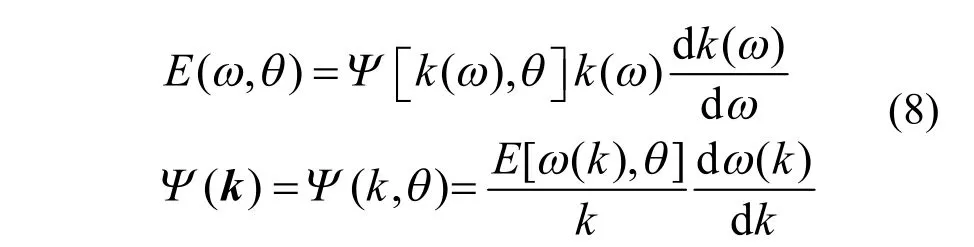
E(ω,θ) 可以进一步写为:

海浪谱、方向分布函数主要来自于对海浪的长期观测。用测波仪、合成孔径雷达(Synthetic Aperture Radar, SAR)、船载雷达(Marine Radar)等对海浪进行观测,对观测数据进行谱估计,进而得到海浪谱、方向分布函数以及相关参数。
2.2 Phillips谱的频率谱和方向分布函数
显然,Phillips谱 Ph(k)是一个瞬时空间谱。由于:

则 Ph(k)可写为:
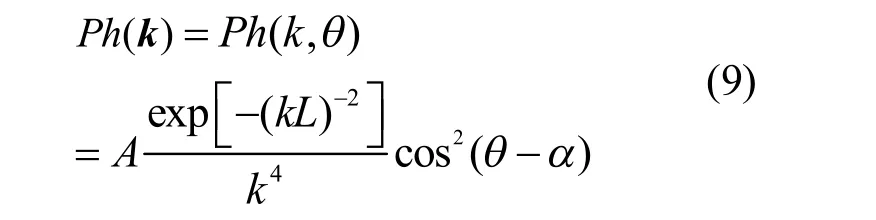
令 EPh(ω,θ)、 DPh(θ)和 SPh(ω)分别为Ph(k)对应的方向谱、方向分布函数和频率谱,由式(8)和式(9)可得:
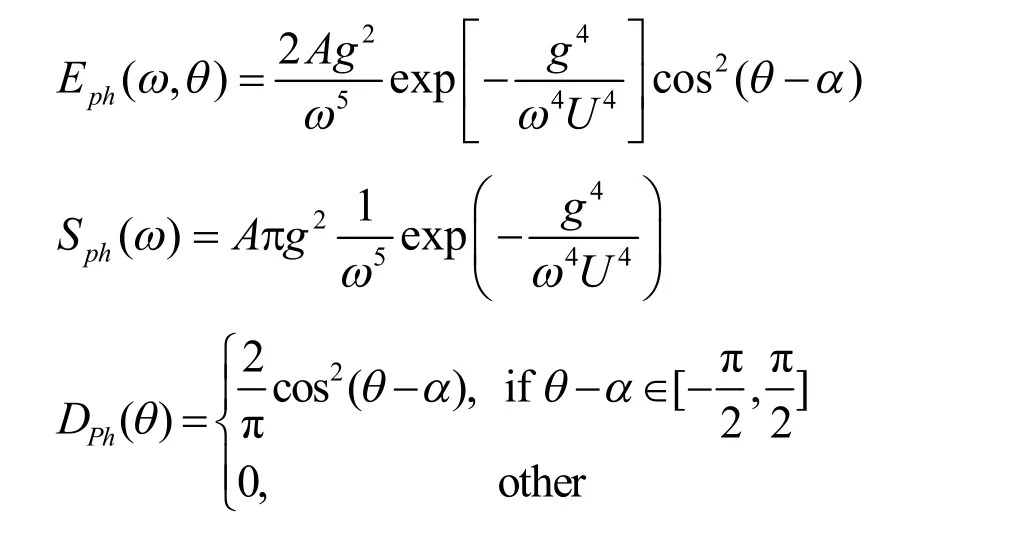
其中,DPh(θ)为 n= 1的cos- 2n分布的方向分布函数,该形式也是国际拖曳水池会议(International Towing Tank Conference, ITTC)推荐的方向分布函数。
2.3 Phillips谱常数A的计算
P-M谱是一种常用的频率谱,P-M谱的表达式为:

式中,α、β均为常数,α= 8.1× 10-3,β=0.74;U19.5为距离海面高度为19.5m处风速。
比较 SPh(ω)和 SPM(ω)发现两者有一定的相似性:
(1)两者都符合 Neumann形式。所谓Neumann形式,即:

式中,A、B中包含风要素或波要素。迄今为止提出的许多波浪谱,很大一部分符合这一形式。对于 SPh(ω),p= 5,q= 4;对于 SPM(ω),p= 5,q= 4。
(2)对风的描述仅包括风速,不包括风距和风时。
(3)两者的谱宽度相等。谱宽度反映谱内能量的集中程度,用υ表示,υ= (m0m2/-1 )1/2,υ∈ (0,1)。经计算υPh= υPM,SPh(ω)和 SPM(ω)谱宽度相同,具有相同的能量集中程度。
SPh(ω)、 SPM(ω)的0阶谱矩为:

P-M谱是经过长期观测所获得的,所依据的资料比较充分,使用方便,可以直接积分,在海洋工程和船舶工程中得到广泛应用,基于上述理由在计算Phillips谱常数A时参考了P-M谱。为此假设 SPh(ω)的风速也为 U19.5,且在相同风速下Phillips谱和P-M谱的成员波具有相同的单位面积波能,即:,则A= 3.48× 10-3。
1)Phillips谱和P-M谱的部分大波平均波高相等。所谓的部分大波平均波高,是指将波高按大小依次排列,令 a> 1,则其中最高的1/a部分的平均值,称为1/a部分大波的平均波高,以 H1/a表示,可以用下式计算:

2)Phillips谱和P-M谱的平均波高相等。平均波高的计算如下式:
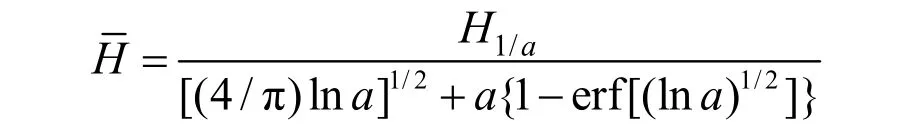
从上式可得,若两谱的部分大波平均波高相等,则平均波高也相等。
当风速值相等时,P-M谱和Phillips谱的 m0、部分大波平均波高、平均波高相等,所以假设Phillips谱的风速为距海面高度 19.5m处风速是合理的。随着风速增加, m0增大, H1/a和也会增加。即随着风速的增加,波高变高,波浪更加汹涌,这与真实海浪是相符的。
图 1 是 用 Phillips 谱 的 绘 制 效 果(= 9.6 m/s ,α'= 180°)。

图1 Phillips谱的绘制效果图
3 使用其他形式的谱绘制海浪
在基于统计和谱的方法中,除了使用Phillips谱,还应尝试使用其他谱,进而对绘制结果进行比较,从中选择适合于航海模拟器中海浪绘制所使用的谱。第 2部分中作者已分析了Phillips谱的频率谱、方向分布函数,指出其频率谱 SPh与P-M谱相似,其方向分布函数为 n=1的cos-2n形式,因此作者首先尝试用 P-M 谱和cos-2s形式方向分布函数构造瞬时空间谱ΨPM-cos2s(k )绘制海浪。由于 ΨPM-cos2s(k )谱和Phillips谱对风的描述仅包括风速,不包括风距等其他风的参数,海浪观测表明风距等参数也对海浪产生影响,因此作者还构造了瞬时空间谱ΨJ-Po(k )以绘制了海浪。 ΨJ-Po(k)的频率谱为JONSWAP谱,该谱中风的参数包括风速及风距。ΨJ-Po(k)的方向分布函数作者采用了 Poisson分布形式。
3.1 使用 Ψ PM -cos2s(k)谱绘制海浪
用P-M谱和 s= 2的cos-2s形式方向分布函数构造方向谱 EPM-cos2s(ω,θ):


图 2 是 使用 ΨPM-cos2s(k )绘制的海浪(U19.5= 9.6 m/s ,α'= 180°)。

图2 Ψ PM -cos2s(k)谱的绘制效果图
3.2 使用 Ψ J-Po(k)谱绘制海浪
Phillips谱和 ΨPM-cos2s(k)均为无限风距的谱。风距指的是风接近于不变的方向和速度时在开阔的水面上吹过的距离。因此采用Phillips谱和 ΨPM-cos2s(k)绘制海浪,仅能描述风速对于海浪的影响。而JONSWAP谱对于风的描述,就包括了风距。JONSWAP谱的形式为:


使用JONSWAP谱和Poisson形式方向分布函数构[14]造方向谱:


图 3 是 使 用 ΨJ-Po(k )绘 制 的 海 浪(U10= 8 m/s,α' = 180°,X= 50km,γ= 3.3)。

图3 Ψ J-Po(k)谱的绘制效果图
4 绘制结果的比较
1.1 节中对k的采样可改写为:
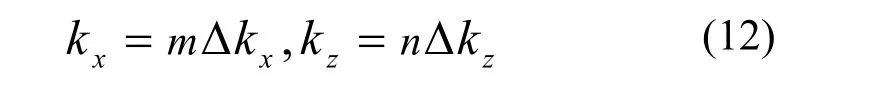
其中:

则当绘制海域面积 Lx× Lz一定, Δ kx和 Δ kz均为常数。在进行2D IFFT中,只有谱值为非0的采样点才会对计算结果产生影响,谱值为0的采样点不会对计算结果产生影响。 Ψ (k)是一个单峰函数,非0的谱值分布在谱峰附近,因此对k进行采样计算 Ψ (k)值,仅需采样谱峰附近 Ψ (k)值非0的k。可对采样进行改进以减小采样点数量,降低 IFFT计算量,则令式(12)中m和n的范围为:

其中, Ms≤ M, Ns≤ N。当 Lx= Lz=1024、M=N=256时,令 Ms= Ns= 128即可完成k的采样。图4为此条件下对 ΨPM-cos2s(k)进行采样。

图4 Ψ PM - cos2s(k )采样
作者测试了使用3种谱绘制海浪的帧率。测试采用中等配置PC机(CPU:Intel E7400,内存:2G,显卡:NVIDIA GeForce GT 430)。当时,使用改进采样法3种谱绘制帧率皆为70f/s,如果采用原采样法,帧率为 61f/s;当时,使用3种谱绘制的帧率皆为33f/s,如果采用原采样方法帧率为26f/s。在相同计算机硬件条件下,当M、N、 Ms、 Ns值相同时,仅更换所用的谱不会影响绘制帧率。
对应选择什么样的谱用于航海模拟器中海浪的实时绘制,作者认为应从两方面考虑:①该谱中风的参数不仅要包括风速,还要包括风距,这样可以使绘制结果体现风距对绘制结果的影响;②由于大部分 D(θ) 中生成波的分布范围在风向的(π]范围内,只有少数 D(θ)生成波限制在风向范围内[14],因此作者推荐使用的 D(θ)。ΨJ-Po(k )谱的绘制结果能体现风距对海浪的影响,该谱的,因此,作者认为在上述3种谱中,ΨJ-Po(k)谱较之于另外两者更适合于航海模拟器。
5 总结与展望
文中指出了目前绘制海浪广泛使用 Phillips谱在使用过程中遇到的问题:其一,常数A的取值或取值准则没有给出;其二,谱中对风速没有详细说明。这两点将直接影响到绘制结果能否准确体现风对于海浪的影响。如果要用Phillips谱进行海浪绘制,则需要解决这两个问题。
因此作者首先对 Phillips谱进行了分析,发现 Phillips谱是一种瞬时空间谱,其频率谱SPh(ω)符合Neumann形式,且 p= 5、 q= 4,其方向分布函数为ITTC推荐的形式。 SPh(ω)只包含风速,与P-M谱相似,且两谱的谱宽度相同。于是在假设Phillips谱和P-M谱具有相同单位面积波能的前提下计算出Phillips谱的常数A,并参考P-M谱对Phillips谱的风速详细说明。
除了 Phillips谱,在基于统计谱的方法中还可以采用其他形式的谱,对这些谱的绘制结果进行比较,以选择适合航海模拟器的谱。为此作者构造了 ΨPM-cos2s(k)谱和 ΨJ-Po(k)谱,并用两者绘制了海浪。 ΨPM-cos2s(k)谱的频率谱为 P-M谱,方向分布函数为cos-2s形式;ΨJ-Po(k)谱的频率谱为JONSWAP谱,方向分布函数为Poisson形式。作者对使用 Phillips谱、 ΨPM-cos2s(k)谱和ΨJ-Po(k)谱的绘制结果进行了比较。通过比较发现,使用 Phillips谱和 ΨPM-cos2s(k )谱的绘制结果能反映风速和风向对于海浪的影响,但是不能反映风距对海浪的影响;而使用 ΨJ-Po(k)谱的绘制结果能反映风速、风向及风距对于海浪的影响。在相同的计算机硬件条件下,采样点数量相同时,使用3种谱绘制的帧率相同。
通过上述研究,作者认为航海模拟器所选择谱的风参数应包括风速、风向、风距,这样使得绘制结果能较为完整地反映风对海浪的影响。因此 ΨJ-Po(k)谱较之于另外两者更适合于航海模拟器。
本文方法所绘制的海浪,有助于提高船舶驾驶员模拟器培训的质量。船舶在海上航行,会受到海浪的影响,海浪还可能危及航行安全。作者曾为此请教过几位有经验的船长,他们普遍认为:航海模拟器培训为受训船舶驾驶员对大风浪中船舶操纵提供感性认识,从而使受训船舶驾驶员获取大风浪中船舶安全航行的经验和对策。了解船舶在风浪中的运动,有助于船舶操纵的安全[20]。本文所进行的研究有助于在模拟器中更准确的体现风对于海浪的影响,使得受训的船舶驾驶员能更好地理解风及海浪对于船舶运动状态的影响以及应该采取何种操船措施使得船舶处于安全状态,提高模拟器培训效率。
今后的工作将继续致力于改善海浪的绘制效果,使其更加逼真。尝试运用大连海事大学实习船“育鲲”号上装备的雷达波浪检测仪和方向谱波浪仪对海浪进行深入观测,得到更为真实的波浪谱用于海浪绘制。
[1] Mihalef V, Metaxas D, Sussman M. Animation and control of breaking waves [C]//Proc of the 2004 ACM SINGGRAPH / Eurographics Symposium on Computer Animation. New York, US: ACM Press, 2005: 315-324.
[2] Pritchard P. Fluid mechanics: SI version [M]. 8th ed. Singapore: John Wiley & Sons (Asia) Ptc Ltd, 2011: 2-10.
[3] Muller M, Solenthaler B, Keiser R, Gross M H. Particle-based fluid-fluid interaction [C]//Proc of EUROGRAPHICS ACM SIGGRAPH Symposium on Computer Animation. New York, US: ACM Press, 2005: 237-244.
[4] 延 诃, 王章野, 廖斌斌, 黄若冠, 彭群生. 基于物理的海浪场景的真实感建模与绘制[J]. 计算机辅助设计与图形学学报, 2008, 20(9): 1117-1124.
[5] 陈 曦, 王章野, 何 戬, 延 诃, 彭群生. GPU中的流体场景实时模拟算法[J]. 计算机辅助设计与图形学学报, 2010, 22(3): 396-405.
[6] Fourier A, Reeves T. A simple model of ocean waves [C]//Proc of the 13th Annual Conference on Computer Graphics and Interactive Techniques. New York, US: ACM Press, 1986: 75-84.
[7] Yuksel C. Real-time water waves with wave particle [D]. College Station, Texas: Texas A&M University, 2010: 29-40.
[8] 苏玉民, 付金丽, 王 卓. 基于三维随机海浪交互式仿真技术研究[J]. 系统仿真学报, 2012, 24(1): 175-179.
[9] Tessendorf J. Simulating ocean water [DB/OL]. http://graphics.ucsd.edu/courses/rendering/2005/jdewa ll/tessendorf.pdf, 2013-2-28
[10] Michel J. Real-time synthesis and rendering of ocean water [EB/OL]. http://citeseerx. ist.psu.edu/ viewdoc/ summary?doi=10.1.1.70.9112, 2013-3-24.
[11] 任鸿翔. 航海模拟器中基于 GPU的海洋场景真实感绘制[D]. 大连: 大连海事大学, 2009: 27-61.
[12] 赵 欣, 裴炳南. 一种快速的海浪仿真方法[J]. 系统仿真学报, 2012, 24(1): 132-136.
[13] Ochi M. Ocean waves: the stochastic approach [M]. Cambridge, UK: Cambridge University Press, 1998: 21-50.
[14] Cost 714 Working Group 3. Measuring and analyzing the directional spectrum of ocean waves [M]. Brussels, Belgium: EU Publications Office, 2005: 3-20.
[15] 国际海事组织. STCW公约马尼拉修正案履约指南[M].大连: 大连海事大学出版社, 2010: 89-135.
[16] 金一丞, 尹 勇. STCW公约马尼拉修正案下的航海模拟器发展战略[J]. 中国航海, 2012, 35(3): 5-10.
[17] Det Norske Veritas. Standard for certification maritime simulator systems No.2.14, January 2011 [EB/OL].http://exchange.dnv.com/publishing/ StdCert/2011-01/Standard2-14. pdf, 2013-02-24.
[18] 刘大刚, 冷 梅. Meteorology and oceanography for mariners [M]. 大连: 大连海事大学出版社, 2011: 5-7.
[19] Nouguier F, Guérin C A, Chapron B. “Choppy wave”model for nonlinear gravity waves [J]. Journal of Geophysical Research, 2009, 114: 1-16.
[20] 洪碧光, 杨林家. Ship handling [M]. 大连: 大连海事大学出版社, 2012: 315-326.
On Selection of the Wave Spectrum in Ocean Wave Real-time Rendering
Chen Lining, Jin Yicheng, Ren Hongxiang
(Key Laboratory of Marine Dynamic Simulation & Control for Ministry of Communications, Dalian Maritime University, Dalian Liaoning 116026, China)
The Phillips spectrum is widely used in ocean wave real-time rendering. First, the structure of the spectrum is analyzed. The Phillips spectrum is an instantaneous spatial spectrum. Its frequency spectrum is in accord with the spectrum form raised by Neumann and similar to the P-M spectrum. Its directional distribution function is that recommended by the international towing tank conference. On the hypothesis that the wave energy per unit area of the Phillips spectrum equals that of the P-M spectrum, the spectral constant is computed, and the spectral wind speed is clarified. In addition to the Phillips spectrum, other spectra are tried as well. The P-M spectrum and the directional distribution function of cos-2s form are used to construct an instantaneous spatial spectrum, denoted as PM-cos2s form, and the JONSWAP spectrum and the direction distribution function of Poisson form are applied for constructing an instantaneous spatial spectrum, denoted as J-Po from. The comparison of the rendering results of the three spectra shows that the wave rendered with the Phillips spectrum and PM-cos2s spectrum can reflect wind speed influence on the wave, but cannot embody the fetch length influence, while the wave rendered with J-Po spectrum can show the fetch length effect along with wind speed on the wave. With the same computer hardware, the frame rates of the three spectra are equal. For wave rendering in the nautical simulator, the wind parameter of the selected spectrum should contain the wind speed as well as fetch length, and the generated wave of the spectrum should distribute in (-π,π] of the wind speed. So J-Po spectrum is more suitable than the other two for the nautical simulator. The method was used in the nautical simulator.
ocean wave rendering; Phillips spectrum; directional distribution function; wind speed
TP 391.9;U666.158
A
2095-302X (2014)02-0173-08
2013-03-30;定稿日期:2013-05-29
国家973重点基础研究发展规划基金资助项目(2009CB320805),中央高校基本科研业务费专项资金资助项目(2012TD002)
陈丽宁(1981-),男,黑龙江哈尔滨人,助理工程师,博士研究生。主要研究方向为航海仿真。Email:lnchen1981@163.com

