锤击法在细长体两点激振试验中的研究及应用

程鹏斌，李大鹏，赵晨

（中国航空综合技术研究所，北京 100028）

引言

复杂细长体进行振动试验时头部和尾部试验条件差异较大，使用单振动台进行试验无法满足控制要求。两（多）点激振试验通过使用两台振动台在同一轴向上激励试件，可以使振动载荷分布更加均匀、合理，能更真实地展示产品的振动特性[1-3]。多输入多输出（MIMO）试验控制相比单振动台试验更加复杂，在进行两点激振试验前，确定适合的激励点和控制点的位置对MIMO试验控制极其重要，而激励点和控制点的选取需要参考试验件前三阶的模态信息。

在进行两点激振试验前对细长体试验 件进行模态测试可以快速地确定试验件的基本振动特性，为试验控制提供详细的模态信息，选取合适的激振点（即夹具的夹持位置）和控制点。

1 试验控制

1.1 两点激励控制方法

在MIMO试验系统中，一般认为被控系统是线性时不变的系统。如果振动试验系统中有m个驱动信号激励系统和n个响应信号进行控制，那么每一个驱动信号将对所有的控制信号产生作用，驱动信号与控制信号之间的关系可描述为[3-5]:

写成矩阵的形式为：

式中：{C（f）}是控制向量；{D（f）}是驱动向量；[H（f）]是频率响应函数。对式（2）进行变换可以得到驱动信号：

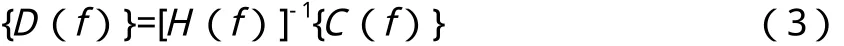
要得到驱动信号，需要对被控系统的频响函数进行求逆。[H（f）]是一个m×n 阶的矩阵，当m=n时，即振动试验的激励点数与控制点数相同，此时[H（f）]是方阵，它的非奇异逆是存在的。

对于随机振动试验的MIMO控制，控制向量{C（f）}使用的是功率谱密度矩阵[Gcc（f）]，相应的驱动矩阵{D（f）}变成[Gdd（f）]，则式（2）变为：

式中：[H（f）]*是控制谱向量[H（f）]的共轭转置。

这时的驱动信号为：

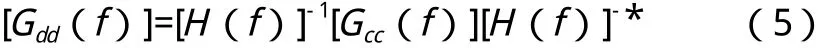
1.2 两点激振试验前需要的模态信息

细长体MIMO振动试验一般采用两个振动台进行激励，通过公式（3）可知，试验时应使用两个控制点进行控制。在两点激励振动试验中，细长体试件动力学的复杂特性会对控制结果造成很大的影响，如果试验时激励点（或夹具的位置）选择不当，特别是选择在振型节线处时，会造成试验件局部响应过大，最终使试验控制超差甚至无法控制，更严重的可能会对试件结构造成损坏；如果控制点选择不当会造成局部的欠试验甚至过试验，如果选择得当，比如选在振型波峰处，在某些控制方式下则能较好控制试验；同时如果已知控制点的模态信息则可以选择合适的控制方式。因此，在设计两点激励振动试验时，有必要首先对试验件开展模态分析，找出容易造成试验控制超差的模态信息[6-8]。

试验件前三阶的模态信息对于两点激振试验的控制具有十分重要的参考意义。试验前需要参考的前三阶模态信息包括：固有频率wi；模态振型波峰，即每阶模态振型极大值点；模态振型节线，即每阶模态振型振动为0的地方。

2 锤击法原理及方法

2.1 原理与优点（见图1）

结构的模态信息由一系列频率、阻尼比和模态振型构成。结构的基本模态信息可以通过模态试验测量出来，目前较为通用的模态测试方法是通过对结构进行激励获取模态信息，常用的激励方式有激振台激励和力锤（锤击）激励。力锤激励属于瞬态激励（或脉冲激励），瞬态激励的工作原理是采用单位脉冲函数对被测结构对象进行激励。脉冲激励的持续时间趋近零，频率范围为无限大，且是连续的，在脉冲宽频信号的激励下，能把试验对象的各阶固有频率都激发出来[3,6]。锤击法是一种最简便的瞬态激励法。锤击法的基本过程是采用力锤对锤击点进行锤击激励，在信号采集点测量激励时的响应，信号采集与分析设备同时采集激励信号和响应信号，通过计算机对激励信号和响应信号解算获取响应的传递函数，进而得出结构基本的模态信息。对于模态测试而言，响应信号一般是信号采集点的加速度信号。

锤击法的优点是：不需要专门的信号源，不会对试件产生附加质量、附加刚度等副作用；激励点的选择不受力锤本身结构的限制，可以在不能安装激振器的部位对试验件进行激励；能方便地在生产现场进行实验；试验数据获得速度快，效率高[2,4]。正是由于上述优点，自20世纪80年代起，用锤击法获取结构模态信息就已成为分析结构特性十分重要的手段和途径，在工程上有广泛的应用。

图1 锤击法测试过程

2.2 锤击测试方法

锤击试验有两种测试方法：第一种方法是在某一固定不变的位置使用加速度传感器采集点测量锤击响应，用力锤在各单元点逐一施加锤击激励，这种情况称为“移动锤击”。游动锤击法一般只需要一个传感器对响应点加速度进行测量。第二种方法是在某一固定点施加锤击，而在其它所有测点测量响应，这一情况称为“定点锤击”。定点锤击要求传感器尽可能多的覆盖设定模型的单元点。

3 锤击法测量 细长体模态实例

仅在细长体的Y向进行两点激振试验，使用某公司Test.lab软件对试验件进行模态测试，测试时使用的传感器为某公司4508型ICP传感器。

3.1 试验件安装

为了测量试验件自由状态下的模态参数，使用橡皮绳把细长体悬挂起来，如图2所示。由橡皮绳和试验件细长体构成的刚体系统模态频率约为1Hz，远小于进行MIMO振动试验时的最低试验频率20Hz，能满足细长体振动试验对试验件弹性支撑的物理要求[8]。

3.2 建立锤击单元模型

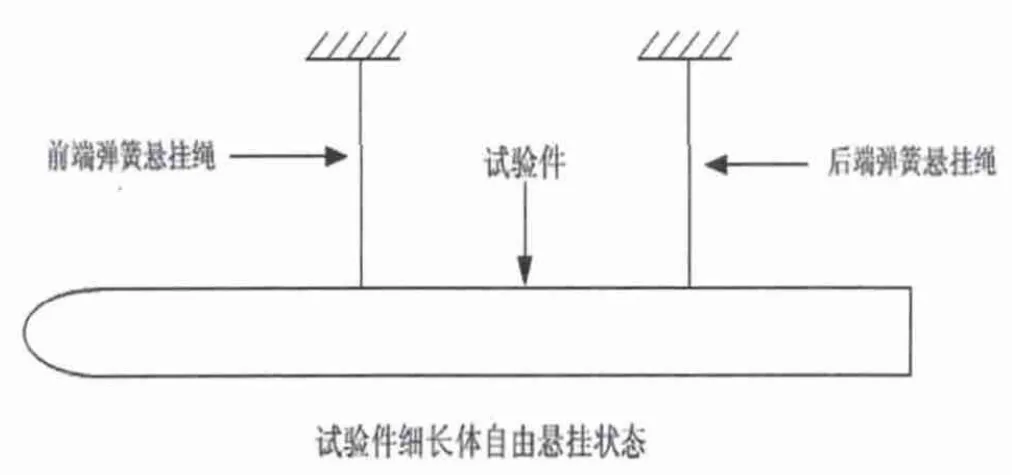
图2 试验件安装

图3 试验件模型

振动试验仅在细长体的Y向进行，因此在模态分析时只用对Y向进行建模，即建立一个细长体的一维模型。在细长体轴向上把细长体的等分为24份，共25个单元点，头部单元点编号为0，尾部单元点为24，如图3所示。0号和24号单元点由于结构原因不能敲击，因此把0号单元点和1号单元点固连在一起，即0号单元点作为1号单元点的随动点。同理把24号单元点和23号单元点固连在一起。选取13号单元点附近区域作为单向ICP传感器（某公司，型号4508）的安装位置。

3.3 进行锤击

选择塑料锤击头对试验件进行锤击。用力锤从1号单元点开始依次对试验件的每个单元点进行锤击，到23号单元点结束。由于每次锤击的力度大小难以掌控，要对每次的锤击结果进行判断，如果锤击的响应在测量范围内则为有效锤击，其结果可以使用，否则锤击响应无效需重新敲击。每个单元点处的有效锤击次数为5次。

3.4 锤击测试结果及分析

经过某公司Test软件对锤击结果的解算，得出细长体试验件的前三阶频率分别为58.0 Hz、135.2 Hz和205.5Hz。前三阶的模态结果见表1，第一、二阶模态振型，如图4所示，23号单元点（24号单元点是23号单元点的随动点）处于细长体尾部，连接方式与其他部位的差异较大，其振型结构并不理想，为了方便分析，不考虑最后两个节点的结果。

4 模态测试结果在两点激振试验中的应用

表1 前三阶模态结果

获取试验件的模态信息后，首先对夹具的位置进行选择，细长体的头部可以使用夹具的位置位于5号单元点和7号单元点之间，尾部可以使用夹具的位置位于15号单元点和18号单元点之间。通过对前三阶模态分析，可以确定试验时卡箍的位置分别位于6号单元节点后方和16号单元节点前方。为控制方便应选择振型中位移较大的点，因此分别选取4号单元节点和16号单元节点作为控制点；根据控制点附近的模态特点，选择两点最大值控制方式进行控制，并对1号单元节点、19号单元节点和22号单元节点进行监测。振动试验激振点、控制点和限制点的正确选择使随机振动试验控制功率谱曲线误差在±3dB以内（图5），满足试验控制的需求，使两点激振试验顺利进行。

图4 第一、二阶模态振型图

图5 头部和尾部两点激振试验控制谱

5 结论

本文采用移动锤击法对细长体试验件进行模态测试，获取了试验件Y向前三阶模态的基本参数，为细长体两点激振试验控制方案的制定提供了充分的模态信息，保证了试验顺利进行。锤击法简单易行，试验设备简单，能在试验生产现场快速测量复杂结构的模态信息，为复杂结构动的振动试验提供便利。

[1] Hamma G. STI multiple vibration exciter control replicates the real world in your laboratory[J]. STI Journal, 1989, 1(2): 1-4.

[2] Heylen W, Sas P. Modal analysis theory and testing[M]. Katholieke Universteit Leuven, Department Werktuigkunde, 2006.

[3] 陈家焱,王海东,周建川 等. 多点激励振动试验控制技术进展[J]. 振动与冲击, 2011, 30(3): 69-73.

[4] 李德葆,陆秋海. 实验模态分析及其应用[M]. 北京:科学出版社, 2001.

[5] 赵怀耘,田光明,钟继根. 两点激励振动试验时结构模态对控制效果的影响分析[J]. 装备环境工程，2012, 9(6): 51-53.

[6] 刘军, 高建立, 穆桂脂 等. 改进锤击法试验模态分析技术的研究[J].振动与冲击, 2009, 28(3): 174-177.

[7] 陈颖,田光明,钟继根.典型细长体结构的两点激励振动试验设计[J]. 航天器环境工程, 2013, 30(1): 68-71.

[8] 徐明. 飞机外挂多输入多输出振动试验技术 [C]. 首届全国航空航天领域中的力学问题学术研讨会论文集 (下册), 2004 : 259-262.