电力系统无功优化的多智能体粒子群算法研究

邢林华，卢道远，陈冬沣，殷 豪，陈思哲，陈智慧

(1．广东电网公司揭阳供电局，广东 揭阳 522000;2．广东工业大学 自动化学院，广州 510006)

无功优化是通过调整补偿电容、变压器变比和发电机端电压等手段来改善系统电压、降低系统损耗，提高电能质量，是电网经济运行的一种有效方法［1］。从本质来说，无功优化是一个非线性、有约束和离散的优化问题，在这一领域已有很多方法，如非线性规划、线性规划、灵敏度分析、二次规划、混合整数法等［2］。文献［3－5］是基于进化算法来进行无功优化，能克服算法容易“早熟”的缺点。文献［6－8］使用混合算法来求解系统多目标无功优化。但是这些方法要求数学是可微的，并且假设各参数是连续的，才能保证求得局部最优解，求解时间比较长。本文提出一种求解电力系统无功优化的新方法，即结合 PSO和 MAS构造了 MAPSO(Multi Agent Particle Swarm Optimization)算法。PSO种群中每一个粒子就是一个Agent，粒子间共同构建了一个球形环境，通过建立一个黑板机制，让A-gent间进行竞争与合作操作和自学习操作，结合粒子群算法的进化机制，更新Agent自身的解空间位置，使其更快，更精确地收敛到全局最优解。最后采用IEEE 14节点系统进行仿真试验，以验证该方法的可行性。

1 配电网无功优化的数学模型

1.1 目标函数

本文采用系统有功网损为目标函数，其约束由罚函数出力，具体如下所示。

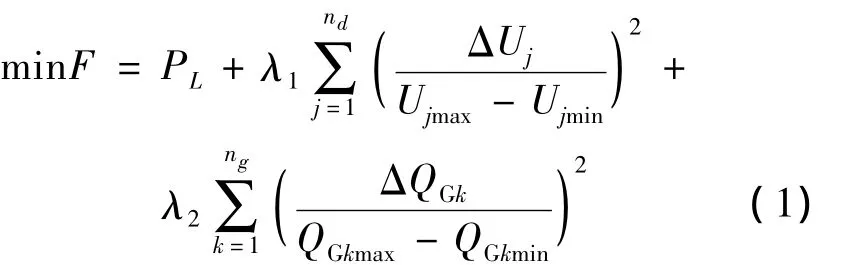
其中

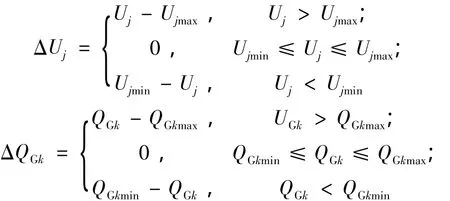
式中:nd为负荷的节点总数;ng为发电机的节点总数;PL为系统的有功损耗;Uj为节点电压;Ujmax、Ujmin分别为节点电压的上、下限;QGk为发电机节点k的无功出力;QGkmax、QGkmin分别为节点k的无功出力上、下限;λ1为负荷节点电压越界惩罚系数;λ2为发电机无功出力越界惩罚系数。

1.2 功率约束

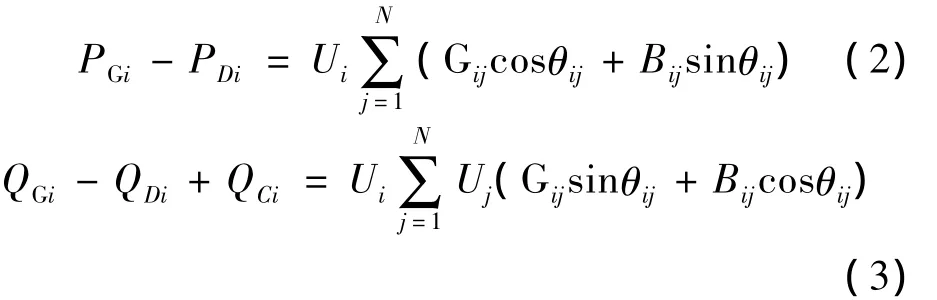
式中:PGi、QGi为节点i的发电机有功出力和无功出力;PDi、QDi为节点i的负荷有功功率和无功功率;QCi为节点i的无功补偿容量。

1.3 变量约束

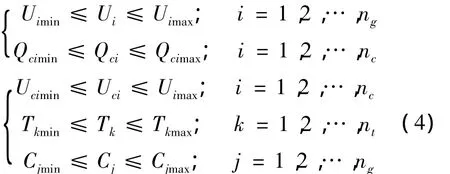
式中:Ui为节点i的电压幅值;QCi为第i台发电机的无功出力;Uci为第i台发电机的端电压;Tk为第k台变压器的变比;Cj为第j台可投切电容器的补偿容量。

2 MAPSO算法

2.1 PSO算法

PSO算法于1995年由Kennedy和 Eberhart首先提出，它是基于个体的改进、种群的协作与竞争机制的进化方法，具有理论简单、收敛速度快和易于编码实现等特点［1］。在PSO算法中，粒子的速度和位置的更新速度表达式为:

式中:k为迭代的次数;w为惯性权重;c1为自学习因子;c2为全局学习因子;r1、r2分别为［0，1］区间随机数;pi为单个粒子的个体历史的最优值;pg为所有粒子的全局最优值;xi为粒子的位置;vi为粒子的速度。

2.2MAPSO模型

2.2.1 体系拓扑结构

本文提出的算法模型如图1所示。

图1MAPSO体系结构Fig.1 Architecture of MAPSO

从图1可以看出，该平台主要活动着一个黑板Agent(Middleware)和一组个体Agent(Individual)，它们分布在不同的网络节点上。其中Middleware负责粒子间竞争、合作，得出全局最优解Pg的操作，而Individual代表着粒子群算法中的一个粒子。实际上，每个个体Agent分别代表着一个潜在解，个体Agent是PSO算法的承担者，是进化机制真正的执行者。而Middleware－Agent是算法中的黑板，是纽带作用，能将个体Agent的网损Ploss一一进行对比，得到全局最优解Pg。由于种群中的个体Agent(Individual)能移动到不同的网络节点和不同设备中运行，因此能确保计算的并行性，从而大大提高优化效率。

2.2.2 MAPSO交互实现

MAPSO的实现过程和表达Agent之间的消息传递过程。

步骤1:所有的个体Agent开始随机产生一组初始位置dpos和对应的进化速度dv，将个体最优解Transferdpbest初始化为dpos。

步骤2:所有的个体Agent根据初始位置计算出网损Ploss。

步骤3:个体Agent向中间Agent发送自身的网损Ploss。

步骤4:中间体Agent收集所有个体Agent的网损消息后，将所有的个体Agent的网损排序，选出个体Agent间最少的Ploss，并将最少的Ploss记为全局最优解。

步骤5:中间体Agent向最少网损的个体Agent发送请求。

步骤6:具有最少网损的Agent向中间体Agent发送自身的个体最优解Transferdpbest。

步骤7:中间体Agent将接受到的个体最优解Transferdpbest，设为全局最优解Transferdgbest保存，并广播给所有的个体Agent。

步骤8:个体Agent接受了全局最优解Transferdgbest，根据式(5)、式(6)分别更新自身的位置和速度。

步骤9:根据无功优化的原理，改变相应的充电电容电纳和操作相关的电容补偿装置进行一系列无功补偿。

步骤10:新一代种群所有的Individual根据新的位置计算网损Ploss。如果进化迭代数没有超过最大值，将转到步骤3进行，直到指定的代数为止，否则进入步骤11。

步骤11:中间体Agent输出全局最优解。

3 算法验证对比

为了验证MAPSO算法的优化效果，对IEEE 14节点系统进行了无功优化计算。该系统有20条支路数，2个发电机节点和11个负荷节点。发电机节点为1，节点2、3、6、8为P－U节点，其余的是P－Q节点。具体的网络拓扑结构如图2所示。

3.1 算例仿真参数设置

在MPSO算法当中，种群规模为30，染色体长度iAgentDim=30，每个粒子为一个Agent，繁殖迭代次数=30，惯性常数W=0.7．学习因子 φ1=2，φ2=1。

3.2 算例仿真结果

基于JADE的MAPSO和基于Matlab的PSO二种算法在求解无功优化时的收敛曲线如图3所示。

由图3中可知，MAPSO算法在开始几代下降速度很快，显示了该算法寻优机制的有效性和优越性，并且该算法的计算精度明显优于基于Matlab的PSO。可见，本文提出算法具有较好的收敛性和计算精度。二种算法网损对比如表1所示。二种算法在额定出力下各控制变量的最优值如表2所示。

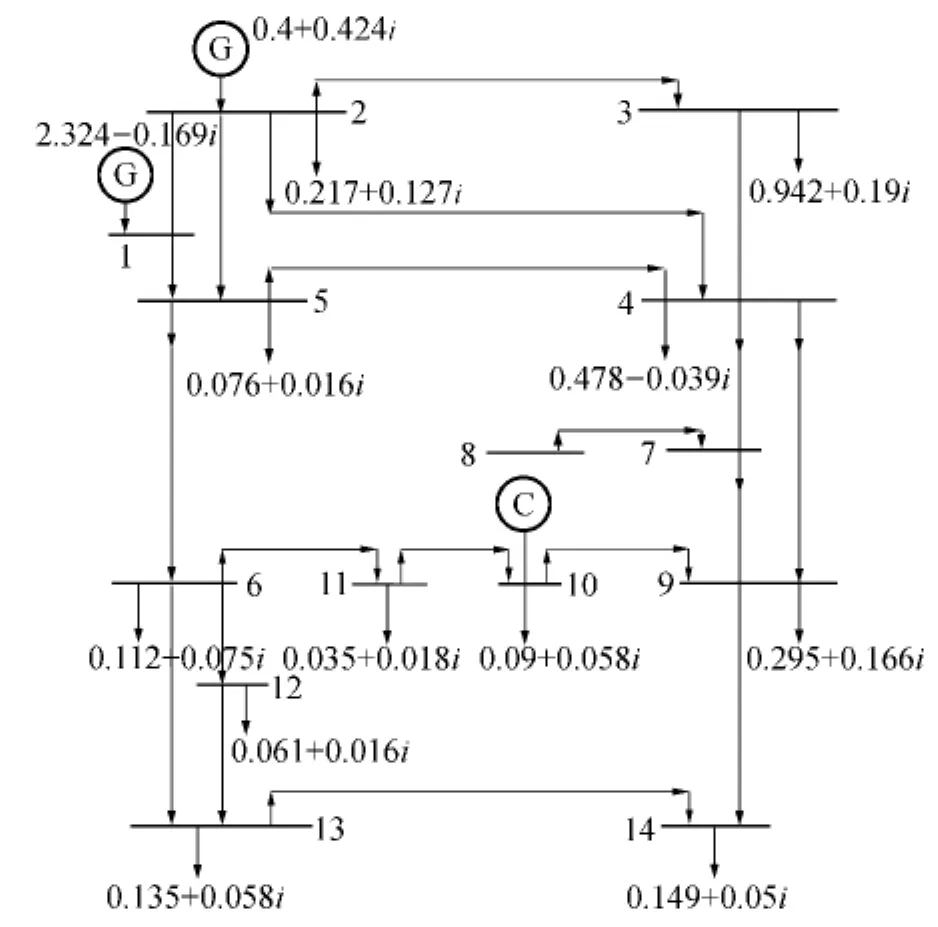
图2 IEEE 14网络结构Fig.2 IEEE 14 network structure

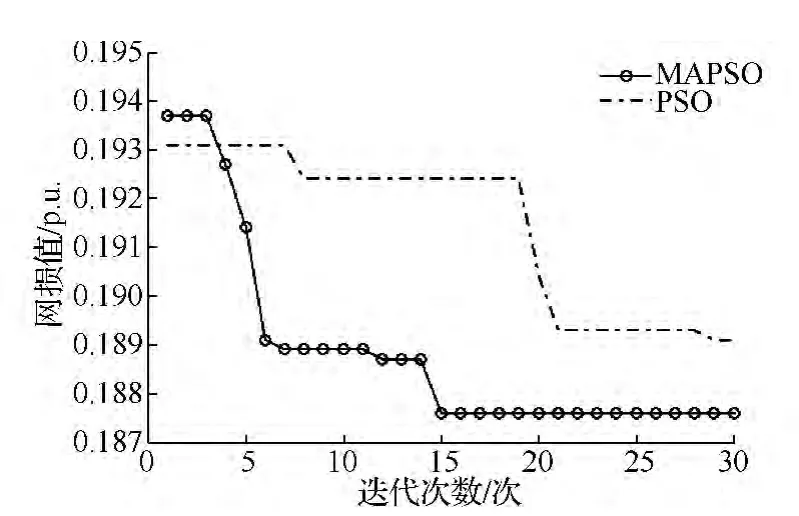
图3 不同算法下收敛特性比较Fig.3 Comparison of convergence properties of different algorithms

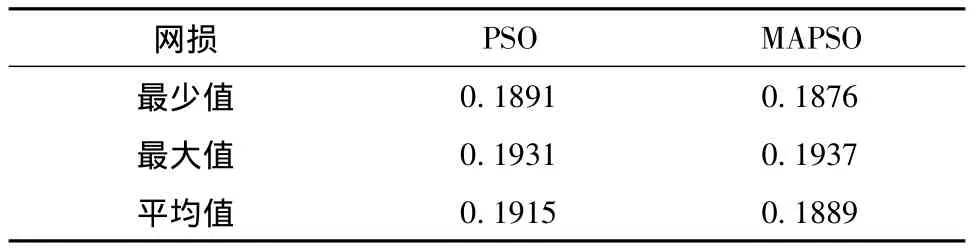
表1 二种算法的网损变化Tab.1 Net losses changes of 2 kinds algorithms

表2 二种算法优化后控制变量值Tab.2 Control variable values after 2 kinds algorithm optimization

由表1可知，MAPSO优化后网损更优，平均网损更少。

4 结论

本文提出的MAPSO具有粒子群算法中粒子间互相竞争与合作，互相学习的优点，同时也兼具MAS分布式的优点，能在多台硬件设备中并发执行任务。通过试验显示，该算法具有较好的收敛性和计算精度。

［1］赵昆，耿光飞．基于改进遗传算法的配电网无功优化［J］．电力系统保护与控制，2011，39(5):57 68．ZHAO Kun，GENG Guangfei．Reactive power optimization of distribution network based on improved genetic algorithm［J］．Power System Protection and Control，2011，39(5):57 68．

［2］ MAMANDUR K R C，CHENOWEH R D．Optimal control of reactive power flow for improvements in voltage profiles for real power loss minimization［J］．IEEE Trans．on PAS，1981，100(7):76 80．

［3］马玲，于青，刘刚，等．基于量子差分进化算法的电力系统无功优化［J］．电力系统保护与控制，2013，41(17):39 43．MA Ling，YU Qing，LIU Gang，et al．Power system reactive power optimization based on quantum DE algorithm［J］．Power System Protection and Control，2013，41(17):39 43．

［4］李秀卿，孙守鑫，张超，等．基于改进细菌群体趋药性算法的无功优化［J］．电力系统保护与控制，2011，39(8):56 59．LI Xiuqing，SUN Shouxin，ZHANG Chao，et al．Reactive power optimization based on the improved bacterial coIony chemotaxis aIgomhm［J］．Power System Protection and Control，2011，39(8):56 59．

［5］曾嘉俊，刘志刚，何士玉，等．一种基于子区域粒子群的无功优化算法研究［J］．电力系统保护与控制，2012，40(1):37 42．ZENG Jiajun，LIU Zhigang，HE Shiyu，et al．Study of reactive power optimization based on sub-region particle swarm algorithm［J］．Power System Protection and Control，2012，40(1):37 42．

［6］王汝田，杨龑亮，王彬，等．模拟渔夫捕鱼寻优算法在多目标无功优化中的应用［J］．电力系统保护与控制，2011，39(21):115 119．WANG Rutian，YANG Yanliang，WANG Bin，et al．Application of optimization algorithm on simulating the fisher fishing in multiobjective optimal reactive power［J］．Power System Protection and Control，2011，39(21):115 119．

［7］罗毅，多靖赞．基于免疫记忆克隆选择算法的多目标无功优化［J］．电力系统保护与控制，2012，40(24):65 70．LUO Yi，DUO Jingyun．Multi-objective reactive power optimization based on immune memory colonial selection algorithm［J］．Power System Protection and Control，2012，40(24):65 70．

［8］李娟，杨琳，刘金龙，等．基于自适应混沌粒子群优化算法的多目标无功优化［J］．电力系统保护与控制，2011，39(9):26 31．LI Juan，YANG Lin，LIU Jinlong，et al．Multi-objective reactive power optimization based on adaptive chaos particle swam optimization algorithm［J］．Power System Protection and Control，2011，39(9):26 31．