粗糙集和层次分析法在配电网规划中的决策研究

马红博

(国网衡水供电公司，河北 衡水 053000)

目前，配电网规划不仅要满足投资和运行费用低的要求，而且要综合考虑系统的可靠性［1－3］、供电质量［4］、环保、系统安全等因素。通常采用的层次分析法(Analytic Hierarchy Process，简称AHP)可以系统地处理定性和不定性的问题［5－6］，但是该方法过于依赖判断矩阵，会导致评价结构准确度的降低。因此，本文在建立配电网指标体系基础上，利用粗糙集中属性约简方法［7］得到属性依赖程度的判断矩阵［8］，对主观和客观权重［9－10］进行有机集成，为配电网规划提供更为合理、科学的决策。

1 层次分析法原理

AHP法由美国学者T．L．Satty提出，将复杂问题分成若干层次，通过专家打分，利用定性和定量相结合的方法确定权重，实质是利用1～9整数及其倒数作为标度构造判断矩阵和一致性的检验［6］。层次分析法处理问题的主要步骤如下:

1)将配电网规划问题分解组合，建立递阶层次结构，建立目标层、准则层和方案层。

2)构造判断矩阵，由n个元素之间相对重要性的比较得到一个两两比较判断矩阵，主观判断矩阵为

式中:aij就是元素ui和uj相对于C的重要性的比例标度。判断矩阵A的元素具有下列性质:aij＞0，aji=1/aij，aii=1。

3)利用式(1)将判断矩阵A的n个行向量归一化后的算术平均值近似作为权重向量，即

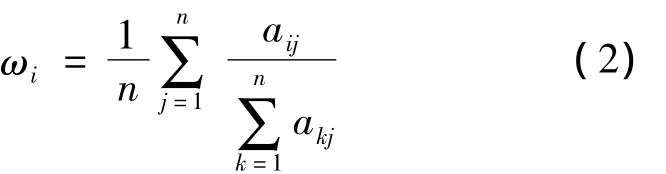
式中:ωi为权重向量的元素;i=1，2，…n。

4)计算最大特征值λmax，并引入相容性指标CI检验判断矩阵的一致性:

一般CI＜0．1时，认为判断矩阵的一致性可以接受;反之，则需要对判断矩阵进行适当修改，改正后再对矩阵重新计算权重并进行一致性检验。

2 粗糙集与客观判断矩阵构造

粗糙集理论是一种处理模糊和不确定问题的工具，在保持分类能力不变的前提下，本文对配电网进行约简［11］，约简准则层和方案层属性。用户指定数据集中的某个或多个属性作为分类决策属性，利用属性选取不同取值，再将数据分成不同类别，从而获取分类规则。

知识库K=(U，R)，对于每一个子集X⊆U，等价关系为R⊆IND(K)，式(4)称为X的R下近似集，公式(5)称为X的R上近似集。

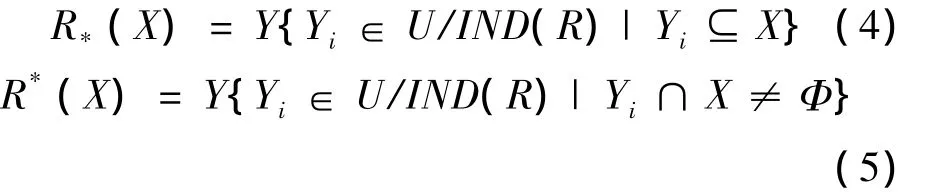
将上近似集和下近似集的差值称为X的R边界集BNR(X)，BNR(X)正区记为POSR(X)=R*(X)，表示个体元素属于X的集合。

设有信息系统S=(U，D，V，f)。其中U为非空对象集合;条件属性为C，决策属性为D，C中包含有n个属性a1，a2，…，an;V是属性值的集合;f是一个信息函数，即f:U×(C∪D)→V，指定了U中每个对象的属性值。

考察所有条件属性样本划分为决策类的分类能力，并确定决策属性对条件属性的依赖度，用r(C，D)表示。去掉条件属性ai后，重新考察分类情况，得到属性ai的重要度r(C，D)－r(C－{ai}，D)。其中C为专家对准则层的属性或者方案层的方案的评价，ai为专家对决策因素i的评价，ai对决策属性D的重要性可以由公式(6)得到，即

采用两两比较的方法，构造类似层次分析法中的判断矩阵，即B=(bij)n×n，bij≥0。

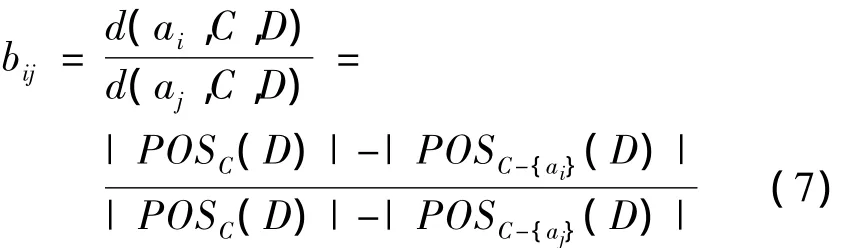
这样利用属性重要度［12］计算得到的判断矩阵很大程度上消除了主观因素的影响，客观真实地的反映了事物属性间固有的联系，此为客观判断矩阵。

3 组合判断矩阵构造

设S=(U，D，V，f)是一个信息系统，A为由层次分析法得到的主观判断矩阵，B是由粗糙集理论得到的客观判断矩阵，C为两者的组合矩阵。

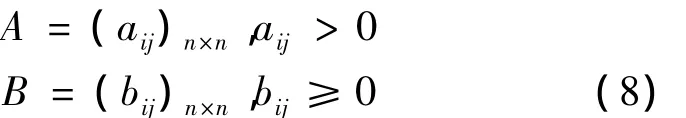
本文建立最优化模型:

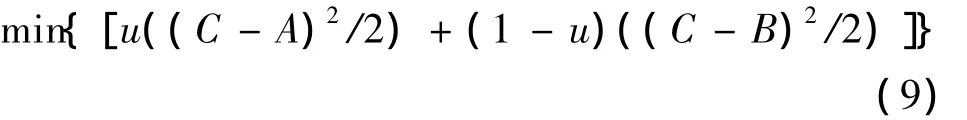
在文献［7］和文献［12］中已经证明公式(9)在可行域Ω上有唯一解，且解为

为此，通过计算组合矩阵的权重来进行决策分析，这样可以避免过分依赖主观因素，又可以避免过分依赖客观因素，从而提高决策的精度。

通过求得组合权重的最优解，建立对象的数学平均值模型。本文设ω(Aj)和ω(aji)为信息系统约简后的准则层和方案层的组合权重，Fij为该对象在属性aij下的取值，得到方案层每一个对象的评价值计算公式:

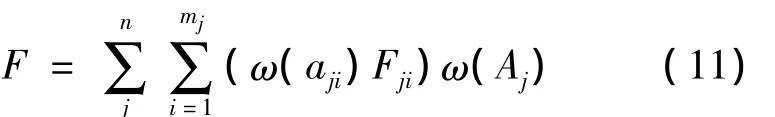
式中:n和mj为信息系统约简后的一级指标和二级指标总的个数。

4 应用算例分析

本文选择上海某小区10 kV配电网规划作为算例，验证该综合评价方法的正确性和可行性。通过分析整理各地配电网历史规划资料，应用AHP法建立配电网综合评价指标体系如图1所示。

运用AHP法求得准则层和方案层内各因素的权重。利用AHP法，对准则层的4个因素a1、a2、a3、a4相对于目标层进行两两比较，得到了准则层中每一个因素的重要度权和矩阵如下表1所示，再求得方案层中的每一个因素的重要度权值和矩阵如表2所示。

图1 配电网规划评价指标体系Fig．1 Distribution network planning evaluation index system

1)首先把图1中方案层中的指标作为信息系统的条件属性集合，将每一层的每一个因素作为条件属性C，f表示决策属性，对应着决策属性D。把要评价的规划方案作为系统中的对象集合，本规划方案中设有11个备选方案，即U={u1，u2，…，u11}。评价中对每一个指标相应的评价结果用“优”、“一般”、“差”3个等级进行衡量，分别用数值3，2，1来代替，从而得到一个信息系统S，如表3所示。类似可以得到准则层的相应专家评价结果如表4所示。

表1 准则层的重要度权和矩阵Tab．1 Importance right and matrix of criterion layer

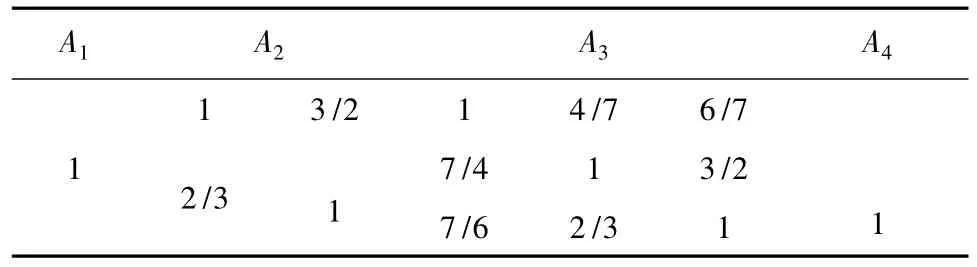
表2 方案层的判断矩阵Tab．2 Judgment matrix of program level

2)对于信息系统S=(U，A，V，f)，经过属性约简相关列后得到初步的简化信息系统，缩减对应的初始指标体系，保留方案层指标为P1、P2、P4、P5、P7，准则层经过计算不能进行属性约简，保留所有指标。最终得到一级、二级指标集合为{A1，A2，A3，A4}={{P1}，{P2}，{P4，P5}，{P7}}。

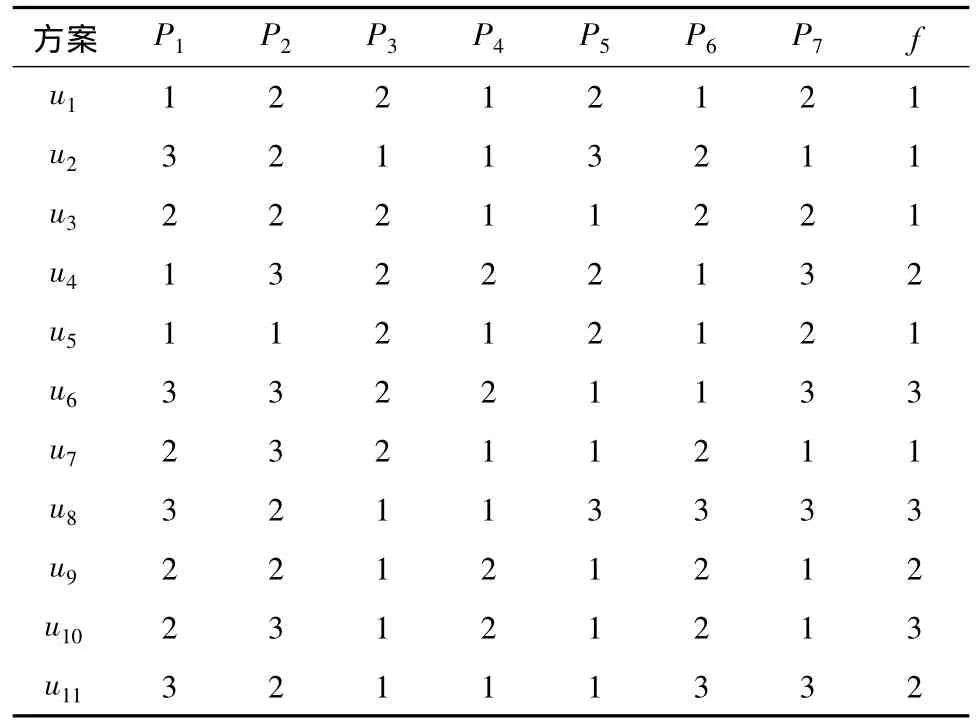
表3 二级指标初始信息系统Tab．3 Two level index initial information system

表4 一级指标初始信息系统Tab．4 Level indicators of initial information system

根据评价指标权重的确定方法，首先计算底层各个指标权重，然后计算更高一层各指标权重，以此类推，选取公式(10)中u的值为0．38黄金分割系数，使主客观权重系数得到合理划分，从而得到准则层、方案层指标的主客观权重和组合权重，如表5、表6所示。

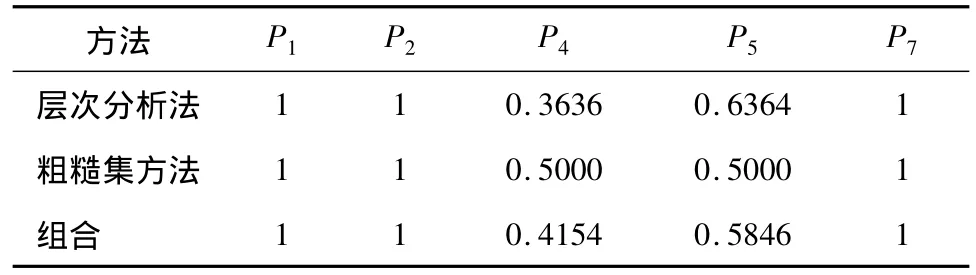
表5 方案层指标权重Tab．5 Program level index weight

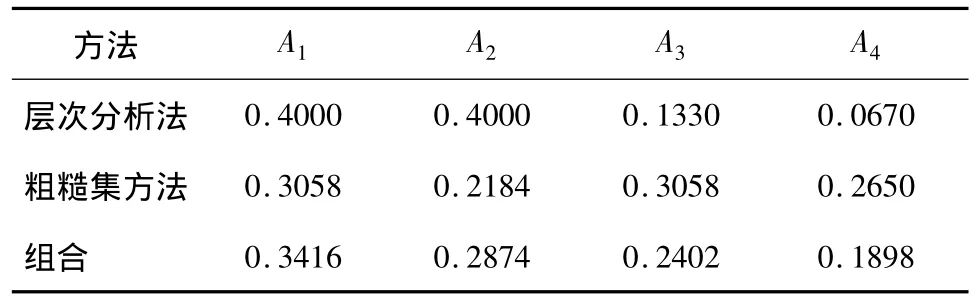
表6 准则层指标权重Tab．6 Criteria layer index weight

根据准则层、方案层指标权重以及每个对象在对应指标下的取值，根据公式可以计算出方案层U中11个对象的评价值分别为1.681、2.318、1.880、2.258、1.394、2.799、1.978、2.697、1.790、2.078、2.412，排序顺序依次为:u6、u9、u11、u2、u4、u10、u7、u3、u9、u1、u5。

根据上述计算结果，本次配电网规划可以按照专家u6的打分结果，建设本次小区配电网。以N－1校验通过率、系统平均停电持续时间、供电能力裕度最优为设计目标，其次考虑系统平均供电可靠率和线损率，最后考虑配电网规划中的设备利用率和单位资产供电能力。

5 结论

1)以粗糙集方法确定客观权重、层次分析法确定主观权重，并将这主、客观权重进行集成，得到组合权重。

2)建立了对象的评价值公式，得到了对象的综合评价模型，并通过实例验证了该模型具有逻辑性、可行性。

［1］桂敏，罗安．申奇男．配电网可靠性评估系统［J］．电力系统自动化，2002，26(24):31-33．GUI Min，LUO An，SHEN Qinan．Evaluation system for distribution network reliability［J］．Automation of Electric Power System，2002，26(24):31-33．

［2］王成山，谢莹华，崔坤台．基于区域非序贯仿真的配电系统可靠性评估［J］．电力系统自动化，2005，29(14):39-43．WANG Chengshan，XIE Yinghua，CUI Kuntai．Distribution system reliability evaluation based on zone non-sequential simulation［J］．Automation of Electric Power System，2005，29(14):39-43．

［3］ LI Weixing，WANG Peng，LI Zhimin，et al．Reliability evaluation of complex radial distribution systems considering restora tion sequence and network constrains［J］．IEEE Trans on Power Delivery，2004，19(2):753-758．

［4］刘伟，郭志忠．配电网安全性指标的研究［J］．中国电机工程学报，2003，23(8):85-90．LIU Wei，GUO Zhizhong．Research on security indices of distribution networks［J］．Proceedings of the CSEE，2003，23(8):85-90．

［5］赵云飞，陈金富．层次分析法及其在电力系统中的应用［J］．电力自动化设备，2004，24(9):85-87，95．ZHAO Yunfei，CHEN Jinfu．Analytic hierarchy process and its application in power system ［J］．Electric Power Automation E-quipment，2004，24(9):85-87，95．

［6］许树伯．层次分析法原理［M］．天津:天津大学出版社，2003．XU Shubo．Theory of analytic hierarchy［M］．Tianjin:Tianjin U-niversity Press，2003．

［7］钟嘉鸣，李订芳．粗糙集与层次分析法集成的综合评价模型［J］．武汉大学学报(工学版)，2008，41(4):126-130．ZHONG Jiaming，LI Dingfang．Comprehensive evaluation model based on rough set and AHP［J］．Engineering Journal of Wuhan University，2008，41(4):126-130．

［8］刘业政．基于rough set理论的判断矩阵构造方法［J］．系统工程学报，2002，17(2):182-187．LIU Yezheng．Constructed methods of judgement matrix based on rough set theory ［J］．Journal of Systems Engineering，2002，17(2):182-187．

［9］刘盾，胡培．一种基于粗集理论的属性权重构造方法［J］．系统工程与电子技术，2008，30(8):1481-1484．LIU Dun，HU Pei．New methodology of attribute weights acquisition based on rough set theory［J］．Systems Engineering and E-lectronics，2008，30(8):1481-1484．

［10］柳炳祥，李海林．基于模糊粗糙集因素权重分配方法［J］．控制与决策，2007，22(12):1437-1440．LIU Bingxiang，LI Hailin．Method of factor weights allocation based on combination of fuzzy and rough set［J］．Control and Decision，2007，22(12):1437-1440．

［11］张文修．粗糙集理论与方法［M］．北京:科学出版社，2001:30-36．ZHANG Wenxiu．Rough set theory and methods［M］．Beijing:Science Press，2001:30-36．

［12］叶军，王磊．一种基于粗糙集和层次分析法的综合评价方法研究［J］．计算机应用研究，2010，27(7):2486-2488．YE Jun， WANG Lei．Research on comprehensive evaluation method based on rough set and AHP［J］．Application Research of Computers，2010，27(7):2486-2488．