电力系统无功优化研究的进展与展望
刘 凯,申小敏,陈志江
(广东工业大学 自动化学院,广州 510006)
电力系统无功优化一直是电力系统研究的重要内容之一,其主要研究内容是在系统结构参数与负荷分布确定的情况下,通过对某些控制变量的优化计算,使该系统的性能在满足特定约束条件的前提下达到最优。无功优化是一个多目标、多约束、动态且具有不确定性的非线性规划问题[1]。它一般涉及到选择无功补偿的地点,投切无功补偿容量,调节变压器分接头位置和选择合适的发电机机端电压等[2]。其中,发电机机端电压是连续的控制变量,而有载调压变压器分接头的档位与投切的电容组数却是离散的控制变量,使无功优化求解过程变得十分复杂。然而,随着电力系统不断发展,无功优化正逐渐应用于电力系统运行各个领域,并对其优化方案和控制手段的要求越来越严格。因此,对现有的无功优化算法进行改进和拓展迫在眉睫。
1 无功优化的数学模型
无功优化数学模型是在系统安全运行和发电机组运行约束条件的前提下,以系统有功网损Ploss最小、电压的偏移量dv最小和静态电压稳定裕度VSM最大为目标所建立的多目标数学模型,该模型表达式如下[3-4]:
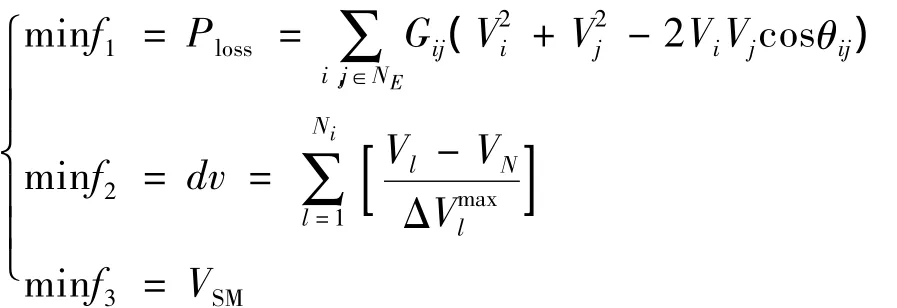
式中:Gij为节点i、j之间的电导;Vi和Vj分别为节点i、j的电压幅值;θij为节点i、j之间的电压相角差;Vl为负荷节点l的实际电压;VN为标准电压;ΔVmaxl为最大允许电压偏差,其中为系统的负荷节点数。
上述多目标的对应约束条件包含潮流方程等式约束、电压幅值约束、无功补偿容量、变压器抽头位置和无功出力等不等式约束。
2 传统的无功优化算法在无功优化中的应用
在20世纪60年代后,许多运筹学上的优化方法都在最优潮流计算中得到了研究和应用。优化方法主要有非线性规划法、线性规划法、混合整数规划法以及动态规划法四大类。另外,比较常用的经典算法有:简化梯度算法、牛顿法、和内点法。
2.1 简化梯度法
1968年,H.W.Dommel和 W.F.Tinney第一次将简化梯度法[5]引入到求解最优潮流问题,此算法的出现对后来无功优化的研究产生了较大的影响。它以极坐标形式的牛顿-拉弗逊潮流计算为基础,首先运用拉格朗日乘子来处理等式约束条件,接着再运用Kuhn-Tucke罚函数来处理不等式约束条件,最后沿控制变量的负梯度方向寻优。但是,简化梯度法在接近最优点时会出现锯齿现象,导致收敛性差,且每次迭代都要重新计算潮流。对此,文献[6]提出了修正的简化梯度法,并引入一个近似的简化海森矩阵的逆矩阵来修正负简化梯度,该方法不仅减少了计算量,避免了数值稳定性问题的求逆过程,而且具有比简化梯度法更快的收敛速度。文献[7]提出了一种改进的简化梯度法,该方法结合简化梯度法和共轭梯度法,充分利用了各自算法的优点,克服了梯度法的很多不足,加快了计算速度。尤其在接近最优点时,运用该方法能得到较好的收敛效果。
2.2 牛顿法
在20世纪80年代,不少国内外专家开始提出用牛顿法求解最优潮流问题。牛顿法是基于非线性规划的拉格朗日乘数法,把拉格朗日函数的二次导数组成的海森矩阵与网络等式方程的一次导数组成的雅克比矩阵再用牛顿法联立求解。牛顿法收敛速度较快,收敛性较好,而且适合应用于节点数很多的大电网[8]。在此基础上,文献[9]对牛顿法最优潮流进行了改进,将发电机节点的有功功率、无功功率以及补偿的无功作为状态量,简化了不等式约束的处理。改进的牛顿法不需要罚函数法,这使得算法程序实现更简捷快速,但该方法不能有效地处理无功优化中大量不等式条件的约束。文献[10]提出了一种新的基于非线性互补问题函数(NCP)的半光滑牛顿方法。通过引入NCP函数,不仅能够增强系统的鲁棒性,而且能有效处理无功优化模型中的不等式约束问题。
2.3 内点法
美国专家Karmarkar在1984年提出了一个线性规划的内点法,20世纪90年代开始把它应用到电力系统最优潮流的优化中。内点法是拉格朗日函数、牛顿法和对数障碍函数法3种方法的组合,该方法不仅继承了牛顿法的优点,而且解决了牛顿法不可避免的试验迭代。然而,如何探测与处理优化过程中的不可求解的问题是内点法的一个难点。文献[11]中提出了原-对偶内点法最优潮流方法,它继承了牛顿法的超稀疏性,克服了牛顿法无法跨越的预估违约约束和迭代过程等缺点,从而使编程简单,计算量小,计算速度快。文献[12]在常规的非线性原-对偶内点法的基础上对修正方式进行了快速解耦和系数矩阵的常数化,提高了其收敛速度与算法稳定性,但高阶修正方程的求解是制约内点法的一个瓶颈。
3 现代人工智能搜索算法在无功优化中的应用
由于传统的优化算法在不同程度上都存在着一些问题。例如,对离散变量的处理缺乏指导性,而且经常求得的是局部最优解。因此,不少专家学者逐渐把研究系统无功优化方法转向人工智能搜索算法。现代人工智能搜索算法的优点是其所具有的“鲁棒性”对无功优化问题提供了较为可靠的解。当今常用的现代智能搜索算法有遗传算法、粒子群算法、多智能体算法等。
3.1 遗传算法
在20世纪70年代初期,遗传算法由美国密执安大学的Holland.J.H教授提出,在20世纪80年代末到90年代初开始运用到电气系统无功优化求解问题当中。遗传算法是把自然界中基于自然遗传和自然选择的理论引入到数学理论中来而开拓的一种全新寻优算法。它是一种自适应全局优化搜索算法,在解决多变量、非线性、不连续和多约束的问题上显示了其独特的优势,即对求解信息要求较少、建模简单、适用领域非常广泛。其主要的缺点是“早熟收敛”及收敛速度较慢。因此,为了改善遗传算法的性能,各种改进的算法也应运而生,其中包括编码方式、适应度函数、选择操作、交叉操作和变异操作,并且这些算法还与其他算法进行组合,进行优势互补。文献[13]针对无功优化中具有连续性和离散性的特点,对原始的遗传算法编码方式交叉算子和变异算子进行了重新的选取,提出了一种改进自适应变异概率遗传算法,通过在算法后期加大变异概率,增大种群多样性。在典型自适应变异概率的基础上,考虑算法所处的阶段,改进自适应变异概率遗传算法,既能保持典型自适应概率较快收敛的特性,又通过在算法后期产生的更多新基因维持种群多样性,它能保持较快收敛的特性并具有更强的寻优能力。通过以往电网实例的优化计算结果表明,在网络电压质量提高时,系统的有功损耗也明显降低了。如文献[14]提出了在不同优化阶段,构造分阶段适应性函数,对目标函数的每个罚因子采用不同的权重,并且引入了选择式杂交方式等改进措施。仿真结果表明,组合的算法大大提高了计算的寻优速度与收敛精度。文献[15]提出了一种基于遗传算法和内点法的无功优化混合策略,它不考虑无功优化中的离散约束,首先采用内点法求解得到初始解,再针对种群个体的不同特点,分别对遗传算法和内点法进行动态调整,使两者的优化结果互为基础,相互利用,从而确保了混合策略的整体寻优效率。文献[16]提出了一种改进小生境遗传算法来克服小生境遗传算法中小生境难以确定的不足,改善遗传算法容易陷入局部收敛和早熟的缺点。算法通过模糊动态聚类方法实现小生境种群的划分,形成小生境进化环境,再利用适应度共享技术调整小生境内个体的适应度,由此提高全局搜索能力;运用隔代小生境共享机制、最优个体邻域搜索及保留策略,改善了算法的计算速度和收敛速度。对节点算例进行了优化计算和分析,结果表明该算法在应用电力系统无功优化问题当中,具有稳定、高效、更好的全局寻优能力等优点。根据生物免疫原理,文献[17]提出了一种免疫遗传算法,它具有抗原识别、记性功能、抗体的抑制和促进等显著特点。免疫算法将目标函数与约束条件当作抗原,把所求问题的解当作抗体。该算法通过亲和度的计算来评价抗体并促进或抑制抗体的产生,以减少进化过程中陷入局部最优解的可能性;通过抗原的记忆功能,很好地保持了个体的多样性。将人工免疫系统中抗体多样性等特点再融入到遗传算法中,形成改进免疫遗传算法(IGA)[18],它采用保优抗体中的免疫疫苗,接种最佳基因的新方法,加快了计算速度,克服了早熟现象,从而提高了局部搜索能力,避免陷入局部最优,加快了计算的速度。
3.2 粒子群算法
粒子群算法是近些年新兴的一类基于群智能的随机优化算法,它是由 Kennedy和 Eberhart在1995年提出的一种模拟鸟群觅食过程中迁徙和群集行为的智能算法[19]。该算法是一种新兴的随机进化搜索算法,具有并行处理特征、鲁棒性强、容易实现等优点。粒子群优化算法(PSO)在搜索的初期收敛速度非常快,在后期容易陷入局部最优,这是普通PSO算法的一个主要缺点。针对传统粒子群优化算法早熟与后期收敛速度慢的缺点,文献[20]提出一种并行自适应粒子群优化算法,该算法首先将初始种群随机划分成若干个子群,然后分别在各子群中提出不同的方法寻优,从而实现了所有子群的并行寻优计算。为避免各子群陷入局部极值点,再采用二值交叉算子使各子群间的信息共享并更新相关粒子位置,在维持了种群的多样性同时保证了算法的全局搜索能力。各子群寻优过程中,根据利己、利他及自主三个方向对当前搜索方向自适应更新,极大地提高了算法的收敛速度。在此基础上,文献[21]又提出了一种基于向量评价的自适应粒子群算法来解决多目标无功优化问题。该算法首先解得问题的Pateto最优解集,再从Pateto最优解集中采用基于决策者偏好及投影寻踪聚类模型来进行不同量纲的多目标整合,最终选取到合适的最优解,进而使结果更加真实可靠。对于有着许多控制变量的大规模实际电网来说,控制变量分布在不同区域使得无功优化问题的求解变得复杂。基于此,文献[22]采用分层控制中的分解-协调思想,将大规模的系统分解成若干个小系统来单独优化。子系统应用协同进化原理,使其对应的解逐渐逼近原问题的最优解。它将大系统的高维解空间分为多个低维解集的组合。结果证明,此方法降低了大规模计算的复杂性,提高了全局寻优能力,避免了过早地陷入局部最优解。针对混合算法在电力系统中的优势,文献[23]提出了基于改进粒子群算法和预测校正内点法的解耦无功优化算法,在时代因子和邻近变异策略基础上,采用分段处理方法对粒子群算法进行改进。利用预测校正算法替代原-对偶内点,使得在内点法寻优过程中的迭代步长增大,同时避免了寻优过程中出现振荡。若分别把改进粒子群算法和预测校正内点算法用于无功优化的离散优化和连续优化子问题上,会使整体的寻优速度更快,效果更佳。文献[24]将混沌优化算法融合到粒子群算法中,提出了混沌粒子群算法应用到求解多目标无功优化问题。该算法采用混沌思想,增加初始化种群的多样性,通过粒子群无功优化算法计算各个粒子对应的适应值,并按照其大小择优选取适当种群进行混沌优化,使无功优化目标跳出局部极值区域,再根据无功优化目标函数值自适应地调整其惯性权重系数,提高局部与全局的搜索能力。通过算例结果分析表明,采用自适应混沌粒子群算法进行无功优化,能够及时跳出局部极值得到全局最优解,且收敛速度快。针对风力不确定性导致粒子适应度不稳定的风电系统,文献[25]提出了基于动态云进化粒子群算法。根据粒子的适应度值,该算法选取优异的个体进行进化,以降低劣性粒子比例,增强搜索速度。通过云发生器,使优异个体进化得到的种群趋于正态分布,从而改善粒子分布,避免“早熟”;动态调节飞行速度,进一步改善粒子分布,提高搜索精度。仿真结果证明了该方法的有效性与结果的可靠性。综合以上所言,粒子群改进的新算法的发展趋势主要包括位置、速度更新公式的改进、控制参数修正、增加种群多样性的算法及算法的混合等。
3.3 差分进化算法
差分进化法是Stom与Price于1995年提出的一种基于种群进化的多点搜索算法,它是现代最好的启发式算法之一。从表面上看,它与PSO算法有相似之处,同时具备遗传算法的一些特征,因此它更像PSO算法与遗传算法的综合。针对多目标多变量复杂问题的寻优方面,它是一种非常具有潜力的优化算法。差分进化算法利用2个随机选取的矢量参数的差向量作为第3个矢量参数的随机变化源,通过对当前种群进行重组、变异和选择等操作产生新一代种群,并逐步使种群进化到包含或接近最优解的状态[26]。传统的差分算法、控制参数是保持不变的,且变异参数决定了收敛速度,而交叉参数对问题的复杂性较敏感,容易过早收敛陷入局部最优。文献[27]应用一种混合差异进化算法,该算法中提出了一种加速操作和种群迁移操作。仿真结果表明,它与单纯的差异进化法、粒子群算法相比,具有收敛度更快、鲁棒性更强、计算精度更高等优点。根据粒子群算法的惯性权重动态调整思想的启发,文献[26]提出一种改进的的差分进化算法,该算法对DE算法的控制参数也采用进化动态调整的策略,根据混沌理论的遍历性,对搜索过程中重叠的个体,利用混沌变量搜索来提高算法的整体搜索能力。测试与算例表明,改进的DE算法更加快速、高效和准确。根据量子计算中的并行、坍缩等特性和算法组合寻优,文献[28]提出了一种基于量子差分进化算法的电力系统无功优化方法,该方法不仅增强了对解空间的遍历能力,而且通过量子计算的概率表达特性来增加种群多样性,从而很好地避免算法的早熟现象,全面提高了全局寻优能力。
4 展望
本文在分析常用的无功优化算法基础上,重点介绍了应用广泛的经典传统算法与人工智能算法,每一种算法都会在原始算法上进行改进,从而使计算的速度与精度得到很大的改善。组合算法通过发挥各自优势,弥补某些缺点来改善算法的寻优效率。组合优化算法在未来需要更深层次的研究与探讨。另外,开发新的智能算法如区间算法[29]、杂草优化算法[30]等应用到电力系统无功优化中也是未来无功优化研究的一个方向。
目前,无功优化相对来说研究得比较成熟。无论是在数学模型还是优化算法上都取得了一定的成果。对于动态的无功优化问题我们研究得较少,今后需要对它作更深入的探索和研究。另外,新的电力系统环境下的无功优化也需要进一步对其探究。
[1]诸骏伟.电力系统分析(上册)[M].北京:中国电力出版社,1995.ZHU Junwei.Power system analysis(Volume 1)[M].Beijing:China Electric Power Press,1995.
[2]陈海炎,陈金富,段献忠.含风电机组的配电网无功优化[J].中国电机工程学报,2008,28(7):40-45.CHEN Haiyan,CHEN Jinfu,DUAN Xianzhong.Reactive power optimization of distribution network containing wind power generators[J].Proceedings of the CSEE,2008,28(7):40-45.
[3] YOSHIDA H,KAWATA K,FUKUYAMA Y.Particles warm optimization for reactive power and voltage control considering voltage security assessment[J].IEEE Transactions on Power System,2000,15(4):1232-12391.
[4]熊虎岗,程浩忠,李宏仲.基于免疫算法的多目标无功优化[J].中国电机工程学报,2006,26(11):102-108.XIONG Hugang,CHENG Haozhong,LI Hongzhong.Multi-objective reactive power optimization based on immune algorit-hm[J].Proceedings of the CSEE,2006,26(11):102-108.
[5] H.W.DOMMEL,W.F.TINNEY.Option Power Flow Solution[J].IEEE Trans on PAS,1968,87(10):1866-1876.
[6]李文沅.求解最优潮流的修正简化梯度法[J].中国电机工程学报,1981:53-61.LI Wenyuan.Optimal power flow solution by modification of the simplified gradient method[J].Proceedings of the CSEE,1981:53-61.
[7]刘学东,王磊,余耀.最优潮流改进简化梯度法的研究及应用[J].山东电力技术,2003,(1):19-22.LIU Xuedong,WANG Lei,YU Yao.Research and application of improved simplifying gradient algorithm in the optimal power flow[J].Shandong Electric Power Technology,2003,(1):19-22.
[8]张力平,何大愚,朱太秀.牛顿法最优潮流与最优无功补偿[J].中国电机工程学报,1987,7(1):11-19.ZHANG Liping,HE Dayu,ZHU Taixiu.Optimal power flow and optimal reactive power compensation by Newton’s method [J].Proceedings of the CSEE,1987,7(1):11-19.
[9]王永刚,彭世康,靳现林.牛顿法最优潮流的改进[J].继电器,2003,31(3):1-5.WANG Yonggang,PENG Shikang,JIN Xianlin.Improved Newton optimal power flow algorithm[J].Relay,2003,31(3):1-5.
[10]张永平,童小娇,吴复立,等.基于非线性互补问题函数的半光滑牛顿最优潮流算法[J].中国电机工程学报,2004,24(9):130-135.ZHANG Yongping,TONG Xiaojiao,WU Fuli,et al.Semi-smooth newton optimal power flow algorithm based on nonlinear complementary problem function[J].Proceedings of the CSEE,2004,24(9):130-135.
[11]李彩华,郭志忠,樊爱军.原-对偶内点法最优潮流在电力系统中的应用[J].电力自动化设备,2002,22(8):4-7.LI Caihua,GUO Zhizhong,FAN Aijun.Application of primal-dual interior point method of optimal power flow to power syst-em[J].Electric Power Automation Equipment,2002,22(8):4-7.
[12]侯芳,吴政球,王良缘.基于内点法的快速解耦最优潮流算法[J].电力系统及其自动化学报,2001,13(6):8-12.HOU Fang,WU Zhengqiu,WANG Liangyuan.Optimal power solution based on fast decouple interior point algorithm [J].Proceedings of the EPSA,2001,13(6):8-12.
[13]靳丹,王维洲,曹俊龙,等.基于改进自适应变异概率遗传算法的无功优化方法[J].电网技术,2012,31(7):6-10.JIN Dan,WANG Weizhou,CAO Junlong,et al.Reactive power optimization method based on adaptive mutation probability genetic algorithm [J].Power System Technology,2012,31(7):6-10.
[14]赵登福,周文华,张伏生.遗传算法在无功优化应用中的改进[J].电网技术,1998,22(10):34-43.ZHAO Dengfu,ZHOU Wenhua,ZHANG Fusheng.Improvement of genetic algorithm in the application of reactive power optimization[J].Power System Technology,1998,22(10):34-43.
[15]刘方,颜伟,DAVID C.Yu.基于遗传算法和内点法的无功优化混合策略[J].中国电机工程学报,2005,25(15):67-72.LIU Fang,YAN Wei,DAVID C.Yu.Hybrid strategy based on genetic algorithm and interior point method for optimal reactive power flow[J].Proceedings of the CSEE,2005,25(15):67-72.
[16]崔挺,孙元章,徐箭,等.基于改进小生境遗传算法的电力系统无功优化[J].中国电机工程学报,2011,31(19):43-50.CUI Ting,SUN Yuanzhang,XU jian,et al.Reactive power optimization of power system based on improved niche genetic algorithm[J].Proceedings of the CSEE,2011,31(19):43-50.
[17]钟红梅,任震,张勇军.免疫算法及其在电力系统无功优化中的应用[J].电网技术,2004,28(3):16-19.ZHONG Hongmei,REN Zhen,ZHANG Yongjun.Immune algorithm and its application in power system reactive power optimization[J].Power System Technology,2004,28(3):16-19.
[18]曾令全,吴昊华,刘琳琳,等.改进免疫遗传算法在DG系统无功优化中的应用[J].电力系统保护与控制,2013,25(5):138-143.ZENG Lingquan,WU Haohua,LIU Linlin,et al.Application of immune genetic algorithm in DG system reactive power optimization[J].Power System Protection and Control,2013,25(5):138-143.
[19] KENNDY J,EBERHART R C.Particle swam optimization[C].Proceedings of IEEE International Conference on Neutral Networks.Perth,Australia,1995:1942-1948.
[20]张文,刘玉田.自适应粒子群优化算法及其在无功优化中的应用[J].电网技术,2006,30(8):19-24.ZHANG Wen,LIU Yutian.Adaptive particle swarm optimization and its application in reactive power power optimization[J].Power System Technology,2006,30(8):19-24.
[21]刘佳,李丹,高立群.多目标无功优化的向量评价自适应粒子群算法[J].中国电机工程学报,2008,28(31):22-28.LIU Jia,LI Dan,GAO Liqun.Vector evaluated adaptive particle swarm optimization algorithm for multi-objective reactive power optimization[J].Proceedings of the CSEE,2008,28(31):22-28.
[22]赵波,郭创新,张鹏翔.基于分布式协同粒子群优化算法的电力系统无功优化[J].中国电机工程学报,2005,25(21):1-7.ZHAO Bo,GUO Chuangxin,ZHANG Pengxiang.Distributed cooperative particle swarm optimization algorithm for reactive power optimization[J].Proceedings of the CSEE,2005,25(21):1-7.
[23]张锋,段余平,邱军,等.基于粒子群算法与内点算法的无功优化研究[J].电力系统保护与控制,2010,38(13):11-16.ZHANG Feng,DUAN Yuping,QIU Jun,et al.Research on reactive power flow based on particle swarm optimization and interior point method[J].Power System Protection and Control,2010,38(13):11-16.
[24]李娟,杨琳,刘金龙,等.基于自适应混沌粒子群优化算法的多目标无功优化[J].电力系统保护与控制,2011,39(9):26-31.LI Juan,YANG Lin,LIU Jinlong,et al.Multi-objective reactive power optimization based on adaptive chaos particle swarm optimization algorithm [J].Power System Protection and Control,2011,39(9):26-31.
[25]王希,王昕,李立学.基于动态云进化粒子群算法的风电系统无功优化方法[J].电力系统保护与控制,2013,41(21):36-43.WNAG Xi,WANG Xin,LI Lixue.Reactive power optimization for wind power system based on dynamic cloud evolutionary particle swarm optimization[J].Power System Protection and Control,2013,41(21):36-43.
[26]刘自发,闫景信,张建华.基于改进微分进化算法的电力系统无功优化[J].电网技术,2007,31(18):68-72.LIU Zifa,YAN Jingxin,ZHANG Jianhua.Power system reactive power optimization based on improved differential evolution algorithm [J].Power System Technology,2007,31(18):68-72.
[27]张丰田,宋家骅,李鉴.基于混合差异进化优化算法的电力系统无功优化[J].电网技术,2007,31(9):33-37.ZHANG Fengtian,SONG Jiahua,LI Jan.Hybrid differential evolution method for optimal reactive power optimization[J].Power System Technology,2007,31(9):33-37.
[28]马玲,于青,刘刚.基于量子差分进化算法的电力系统无功优化[J].电力系统保护与控制,2013,41(17):39-43.MA Ling,YU Qing,LIU Gang.Power system reactive power optimization based on quantum differential evolution algorithm [J].Power System Protection and Control,2013,41(17):39-43.
[29] LUO J,LI W,WANG Q.Checking strong optimality of interval linear programming with inequality constraints and nonnegative constraints[J].Journal of Computational and Applied Mathematics,2014,260:180-190.
[30]左旭坤,苏守宝.多子群入侵杂草优化算法研究及应用[J].计算机工程,2014,40(2):184-188.ZUO Xukun,SU Shoubao.Research and application of multi subpopulation invasive weed optimization algorithm [J].Computer Engineering,2014,40(2):184-188.

